Wahlaufgaben

Wahlaufgabe Arithmetik/Algebra

9.1

Die Summe zweier Zahlen ist 15.
Addiert man zum Doppelten der ersten Zahl das Dreifache der zweiten Zahl erhält man $38.$

Ermittle diese Zahlen.

4 BE

9.2

Am 1. Januar 2022 lag der Durchschnitt der Heizölpreise in Deutschland bei $0,86\,€$ pro Liter.
Am 9. März 2022 erreichten die Heizölpreise ein Rekordhoch von $2,04\,€$ pro Liter.

Berechne, um wie viel Prozent der Heizölpreis erhöht wurde.

3 BE

Zwei Wochen später kosteten 100 Liter Heizöl in Deutschland $163,90\,€.$

Berechne die Ersparnis, wenn man $500$ Liter Heizöl nicht am 9. März 2022, sondern erst zwei Wochen später kaufte.

3 BE

Wahlaufgabe Stochastik

10.1

Ein idealer sechsseitiger Spielwürfel wird zweimal nacheinander geworfen.

Bestimme die Wahrscheinlichkeit dafür, dass zwei gleiche Augenzahlen (Pasch) gewürfelt werden.

3 BE

10.2

Ein Obst- und Gemüsegroßhändler erhält eine Lieferung von $8500$ Melonen. Er möchte die Anzahl beschädigter Melonen ermitteln. Bei einer Stichprobe von $120$ Melonen findet er acht beschädigte Melonen.

Ermittele die zu erwartende Anzahl der beschädigten Melonen in der gesamten Lieferung.

2 BE

10.3

In einem Behälter befinden sich acht gleichgroße Kugeln, die mit den Zahlen $1$ bis $8$ beschriftet sind. Einmalig wird eine Kugel zufällig gezogen.

Die gezogene Kugel soll mit einer Primzahl beschriftet sein.

Gib die Ereignismenge und die Wahrscheinlichkeit für dieses Ereignis an.

3 BE

Alle Kugeln befinden sich wieder im Behälter.

Dann wird aus dem Behälter eine Kugel zufällig gezogen und nicht zurückgelegt. Anschließend wird eine weitere Kugel zufällig gezogen.
Das Ereignis hat eine Wahrscheinlichkeit von $\frac{1}{56}.$

Beschreibe ein Ereignis für diese Wahrscheinlichkeit.

2 BE

Wahlaufgabe Geometrie

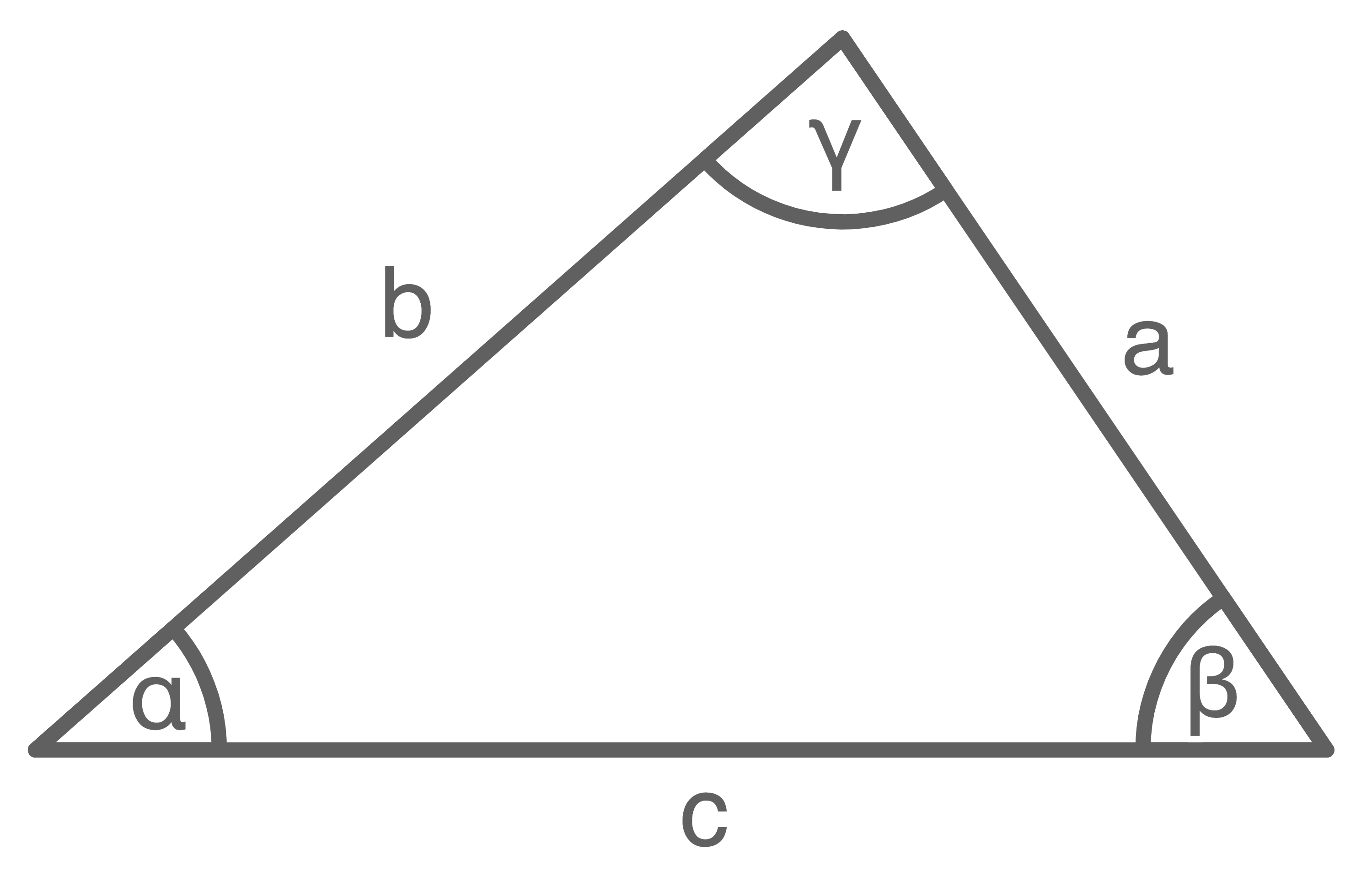
11.1

Skizze nicht maßstäblich

Für das Viereck $EFGH$ gilt:

$\begin{aligned} & \mathrm{e}=12,0 \mathrm{~cm} \\ & \mathrm{h}=5,0 \mathrm{~cm} \\ & \mathrm{f}=\mathrm{g} \\ & \gamma=120^{\circ} \end{aligned}$

Berechne den Flächeninhalt des Vierecks $EFGH.$

7 BE

11.2

Gegeben ist ein Dreieck $ABC$ mit $a=12,0\,\text{cm}; b=15,0 \,\text{cm}$ und $c=18,0\,\text{cm}$ .

Berechne einen Winkel des Dreiecks $ABC.$

3 BE

Wahlaufgabe Funktionen

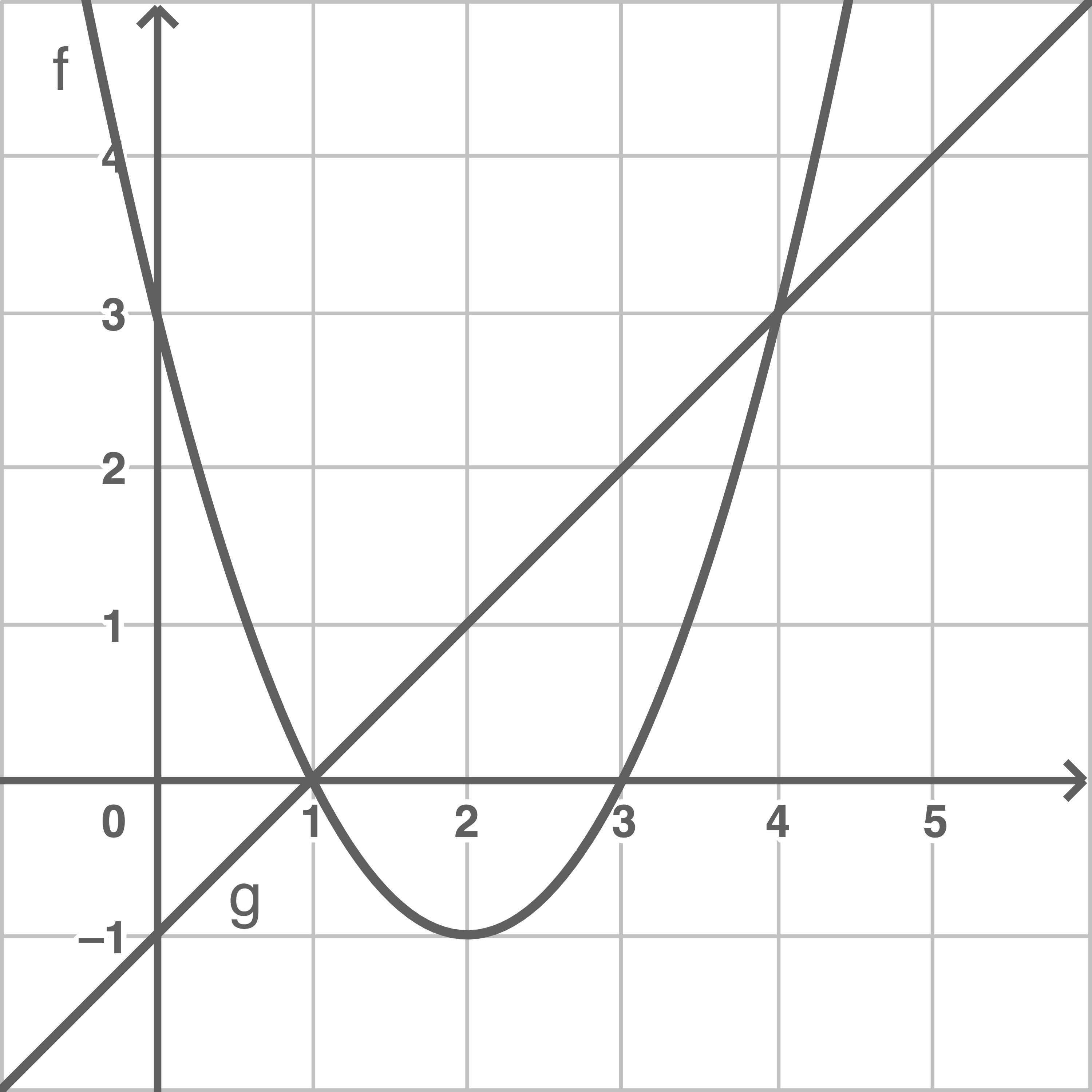
12.1

Gegeben sind die folgenden Funktionen:

$\begin{array}{ll} y=f(x)=x^2-4 x+3 & x \in \mathbb{R} \\ y=g(x)=x-1 & x \in \mathbb{R} \end{array}$

Stelle die Graphen $f$ und $g$ in einem Koordinatensystem $(1 \,\text{LE}=1 \,\text{cm})$ dar.

3 BE

Berechne die Nullstellen der Funktion $f(x).$

2 BE

Die Graphen $f$ und $g$ schneiden sich in den Punkten $P$ und $Q$ . Der Punkt $P$ und die Schnittpunkte der Graphen $f$ und $g$ mit der $y$ -Achse bilden ein Dreieck.

Zeichne das Dreieck ein und berechne den Flächeninhalt dieses Dreiecks.

3 BE

12.2

Gib zwei gemeinsame Eigenschaften der Funktionen $y=f(x)=x^2$ und $y=g(x)=x^4$ mit $x \in \mathbb{R}$ an.

2 BE

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Wahlaufgabe Arithmetik/Algebra

9.1

Es ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& x+y &=& 15 \\ \text{II}\quad& 2x+3y &=& 38 &\quad \\ \end{array}$

Es bietet sich das Einsetzungsverfahren an. Umstellen von $\text{I}$ nach $x$ liefert:

$\text{I}_a\quad x=15-y$

Mit Einsetzen in $\text{II}$ folgt:

$\begin{array}[t]{rll} 2\cdot (15-y)+3y&=& 38 \\[5pt] 30-2y+3y&=& 38 \quad \scriptsize \mid\; -30 \\[5pt] y&=& 8 \end{array}$

Einsetzen von $y=8$ in $\text{I}_a$ liefert:

$x=15-8=7$

Die gesuchten Zahlen sind $x=7$ und $y=8.$

9.2

$\text{Grundwert } G=0,86\,€$

$\text{Prozentwert } W=2,04\,€$

$\begin{array}[t]{rll} p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt] p\,\%&=& \dfrac{2,04\,€}{0,86\,€}\cdot 100\,\% \\[5pt] p\,\%&\approx& 237\,\% \end{array}$

Prozentuale Steigerung berechnen: $237\,\%-100\,\%=137\,\%$

Daraus folgt, dass der Heizölpreis um $137\,\%$ erhöht wurde.

Kosten für $500$ Liter Heizöl am 9. März 2022:

$500\cdot 2,04\,€=1020,00\,€$

Kosten für $500$ Liter Heizöl zwei Wochen später:

$5\cdot 163,90\,€=819,50\,€$

Zwei Wochen später beträgt die Ersparnis $1020,00\,€-819,50\,€=200,50\,€.$

Wahlaufgabe Stochastik

10.1

Wahrscheinlichkeit für eine beliebige Augenzahl: $P=\dfrac{1}{6}$

Es gibt sechs Möglichkeiten, in beiden Würfen die gleiche Augenzahl zu werfen. Mit der Summenregel und der Produktregel folgt:

$P(\text{Pasch})=6\cdot \dfrac{1}{6}\cdot \dfrac{1}{6}=\dfrac{1}{6}$

Die Wahrscheinlichkeit für einen Pasch beträgt $\dfrac{1}{6}\approx 17\,\%.$

10.2

Die Wahrscheinlichkeit für eine beschädigte Melone lässt sich durch die Stichprobe ermitteln:

$P=\dfrac{8}{120}=\dfrac{1}{15}$

Bei $8000$ Melonen werden also $8500\cdot \dfrac{1}{15}=567$ beschädigte Melonen erwartet.

10.3

Die Ergebnismenge ist die Menge aller Primzahlen zwischen $1$ und $8:$

$E=\{2;3;5;7\}$

8 mögliche Ergebnisse

4 günstige Ergebnisse: $2,\,3,\,5,\,7$

Wahrscheinlichkeit für das Ereignis:

$\begin{array}[t]{rll} p&=& \dfrac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl möglicher Ergebnisse}} \\[5pt] &=& \dfrac{4}{8}\\[5pt] &=& \dfrac{1}{2} \end{array}$

Die Wahrscheinlichkeit für das Ereigbnis beträgt $\dfrac{1}{2}=50\,\%.$

Ein mögliches Ereignis ist das folgende:

Es wird die Kugel mit der Beschriftung $6$ und die mit der Beschriftung $7$ gezogen.

Wahlaufgabe Geometrie

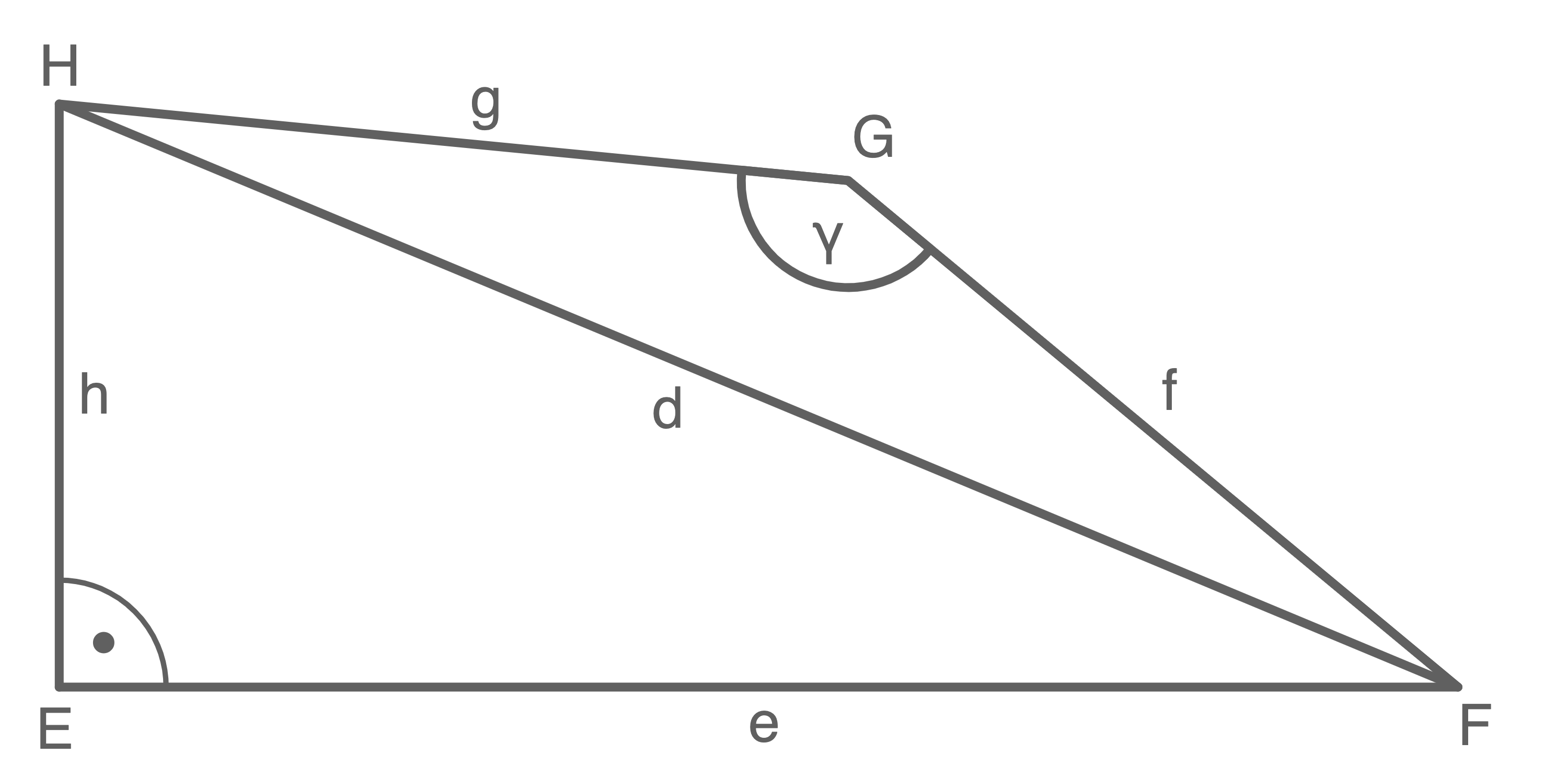
11.1

Flächeninhalt des Dreiecks $EFH:$

$A_{EFH}=\dfrac{1}{2}\cdot 12,0\,\text{cm}\cdot 5,0\,\text{cm}=30\,\text{cm}^2$

Um den Flächeninhalt des Dreiecks $FGH$ berechnen zu können, müssen zunächst einige andere Größen berechnet werden.

Mit dem Satz des Pythagoras gilt für die Länge der Strecke $d:$

$\begin{array}[t]{rll} d^2&=& (12,0\,\text{cm})^2+(5,0\,\text{cm})^2 \\[5pt] d^2&=& 169\,\text{cm}^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt] d&=& 13\,\text{cm} \end{array}$

Wegen $f=g$ ist das Dreieck $FGH$ gleichschenklig und für die beiden Basiswinkel gilt:

$\alpha=\beta=\dfrac{180^{\circ}-120^{\circ}}{2}=30^°$

Mit dem Sinussatz können nun die Längen der Seiten $f$ und $g$ berechnet werden:

$\begin{array}[t]{rll} \dfrac{13\,\text{cm}}{\sin 120^°}&=& \dfrac{f}{\sin 30^°} \quad \scriptsize \mid\; \cdot \sin 30^° \\[5pt] 7,5\,\text{cm}&=& f \end{array}$

Damit gilt ebenfalls $g=7,5\,\text{cm}.$

Mit diesen Größen lässt sich der Flächeninhalt des Dreiecks $FGH$ berechnen:

$\begin{array}[t]{rll} A_{FGH}&=& \dfrac{1}{2}\cdot 7,5\,\text{cm}\cdot 7,5\,\text{cm}\cdot \sin 120^° \\[5pt] &=& 24,4\,\text{cm}^2 \end{array}$

Für den gesamten Flächeninhalt des Vierecks $EFGH$ folgt:

$\begin{array}[t]{rll} A&=& A_{EFH}+A_{FGH} \\[5pt] &=& 30\,\text{cm}^2+24,4\,\text{cm}^2 \\[5pt] &=& 54,4\,\text{cm}^2 \end{array}$

11.2

Skizze

Beispielsweise lässt sich der Winkel $\gamma$ mit dem Kosinussatz berechnen:

Rechenweg anzeigen

$\gamma=82,8^°$

Wahlaufgabe Funktionen

12.1

Bei der Funktion $f(x)$ handelt es sich um eine verschobene Normalparabel. Um diese grafisch darstellen zu können, wird der Scheitelpunkt berechnet:

$y=f(x)=x^2-4x+3$

Es gilt $p=-4$ und $q=3.$

$S\left(-\dfrac{p}{2}\,\bigg \vert \,-\dfrac{p^2}{4}+q\right)$
$S\left(-\dfrac{-4}{2}\,\bigg \vert \,-\dfrac{(-4)^2}{4}+3\right)$

$S(2\mid -1)$

Für die Funktion $g(x)$ wird eine Wertetabelle angelegt.

$\color{#ffffff}{x}$	0	1	2	3	4
$\color{#ffffff}{y=g(x)}$	-1	0	1	2	3

$\begin{array}[t]{rll} f(x)&=& 0 \\[5pt] x^2-4x+3&=& 0 \end{array}$

Es gilt $p=-4$ und $q=3.$ Mit der Lösungsformel folgt:

$\begin{array}[t]{rll} x_{1/2}&=& -\dfrac{p}{2}\pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt] &=& -\dfrac{-4}{2}\pm \sqrt{\left(\dfrac{-4}{2}\right)^2-3} \\[5pt] &=& 2\pm \sqrt{4-3}\\[5pt] &=& 2\pm 1 \end{array}$

$x_1=1\quad x_2=3$

Möglichkeit 1

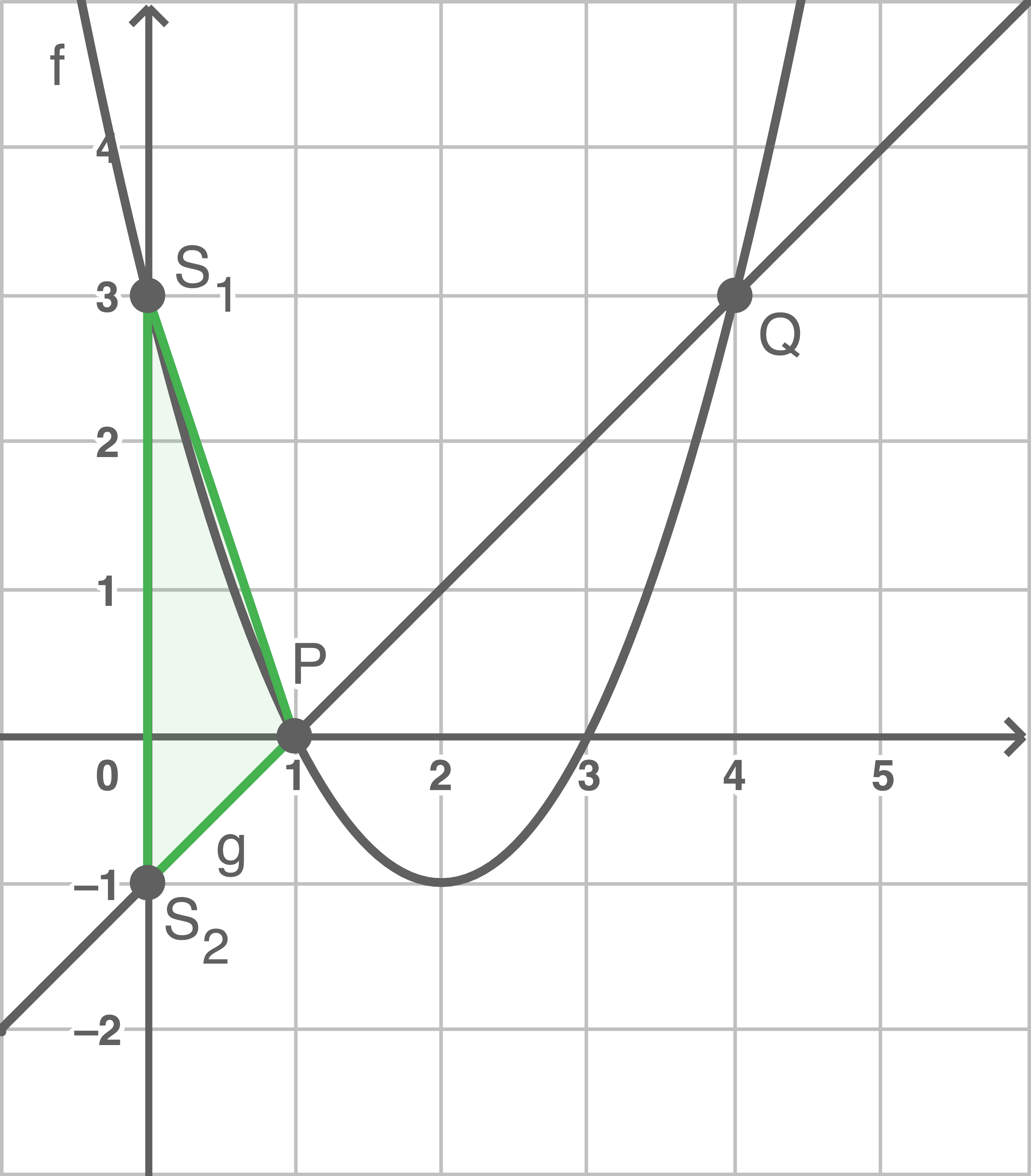Für den Flächeninhalt gilt:

$A=\dfrac{1}{2}\cdot 4\,\text{cm}\cdot 1\,\text{cm}=2\,\text{cm}^2$

Möglichkeit 2

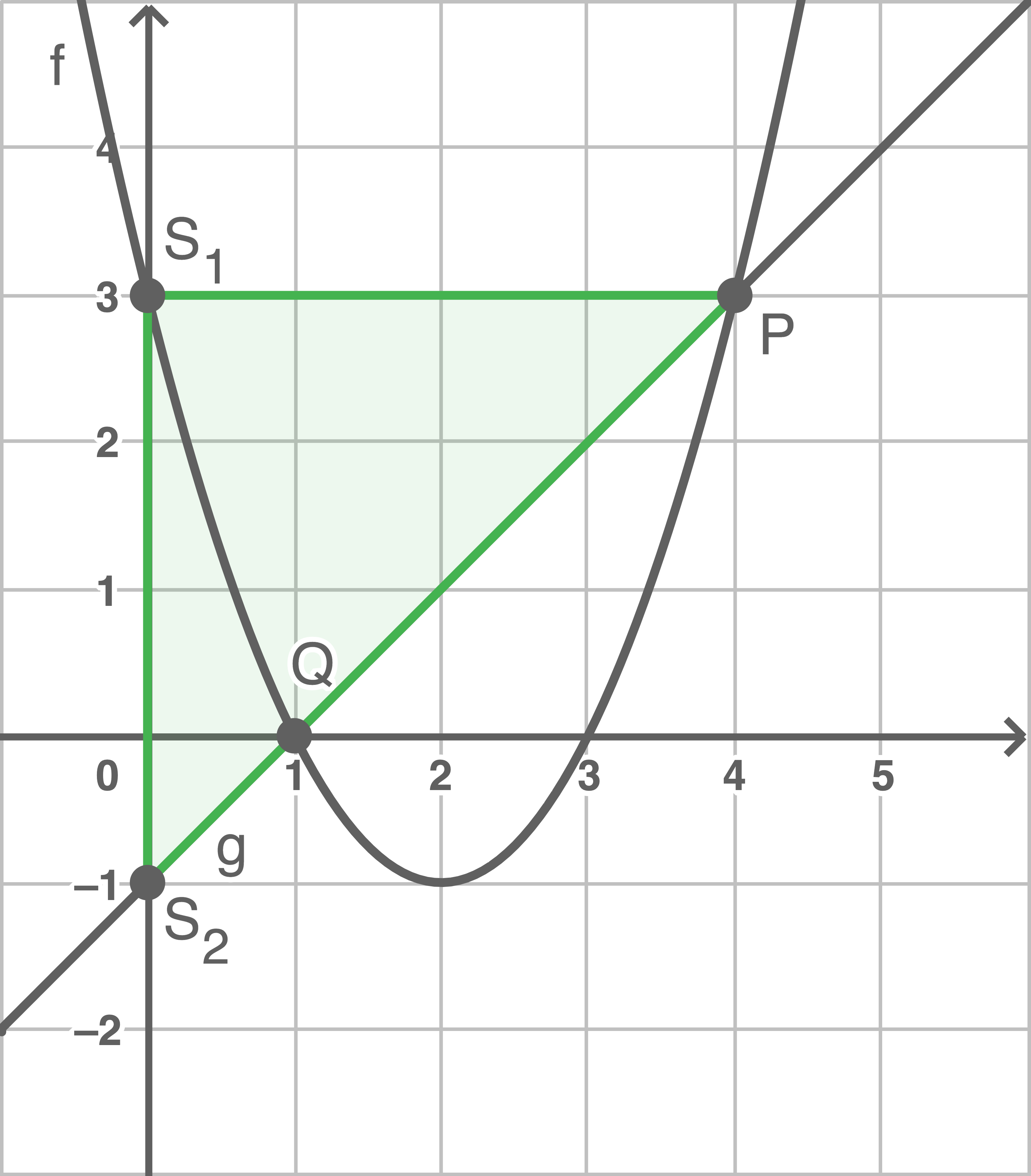Für den Flächeninhalt gilt:

$A=\dfrac{1}{2}\cdot 4\,\text{cm}\cdot 4\,\text{cm}=8\,\text{cm}^2$

12.2

Mögliche Eigenschaften sind die Folgenden:

Die Graphen beider Funktionen haben den Definitionsbereich $x\in \mathbb R, y \geq 0.$
Die Graphen beider Funktionen haben den Wertebereich $y\in \mathbb R.$
Die Graphen beider Funktionen haben den Scheitelpunkt $(0\mid 0).$
Die Graphen beider Funktionen sind symmetrisch zur $y$ -Achse.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?