Pflichtaufgaben 2-8
2
Ein Stück Butter kostete im Januar 2017 durchschnittlich 99 ct, im August 1,99 € und im Dezember 1,55 €.
a)
Auf wie viel Prozent stieg der Preis für ein Stück Butter von Januar bis August?
1 BE
b)
Um wie viel Prozent sank der Preis von August bis Dezember?
2 BE
3
Löse die Gleichung:
2 BE
4
In Salzburg steht das Kunstwerk "Sphaera".
Die Kugel hat eine Masse von
Sie wurde aus glasfaserverstärktem Kunststoff mit einer Dichte von 
hergestellt.
Prüfe rechnerisch, ob die Kugel vollständig aus diesem Kunststoff besteht oder einen Hohlraum hat.
Die Kugel hat eine Masse von
5 BE
5
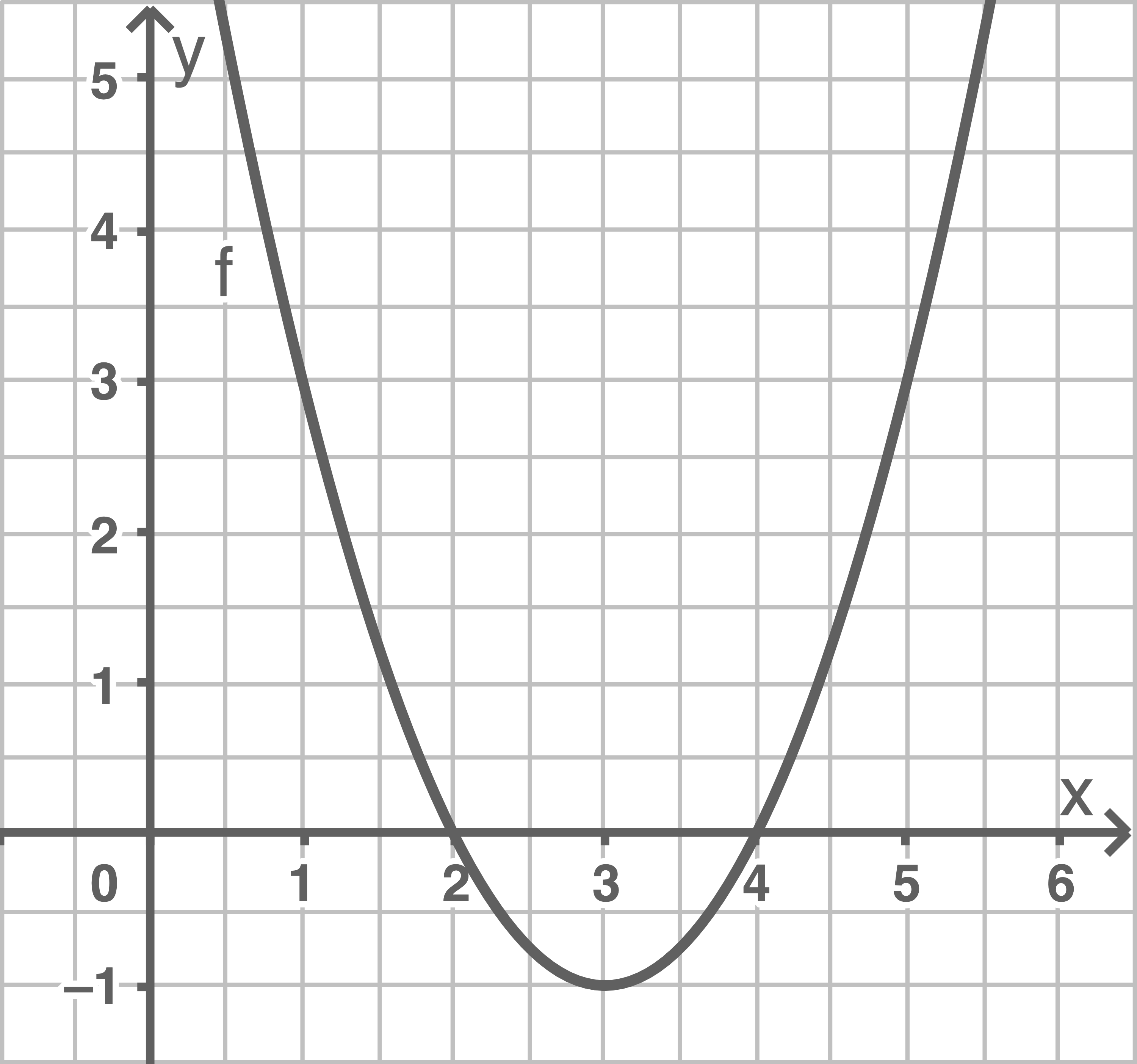
a)
Stelle den Graphen von 
in einem Koordinatensystem dar.
mit 
2 BE
b)
Berechne die Nullstellen der Funktion .
2 BE
6
Auf den Streichholzschachteln eines Herstellers steht: "38 Hölzer".
Bea zählt die Hölzer in einigen Schachteln und notiert:
Eine Schachtel wird zufällig ausgewählt.
Bea zählt die Hölzer in einigen Schachteln und notiert:
| Anzahl der Hölzer je Schachtel | Anzahl der Schachteln |
|---|---|
 |
|
 |
|
  |
|
|
|
 |
|
|
|
|
a)
Ermittle die Wahrscheinlichkeit dafür, dass eine Schachtel mit weniger als 38 Hölzern ausgewählt wird.
2 BE
b)
Gib die Spannweite der Anzahl der Hölzer je Schachtel an.
1 BE
c)
Gib den Median für die Anzahl der Hölzer je Schachtel an.
1 BE
7
Gegeben ist ein Dreieck.
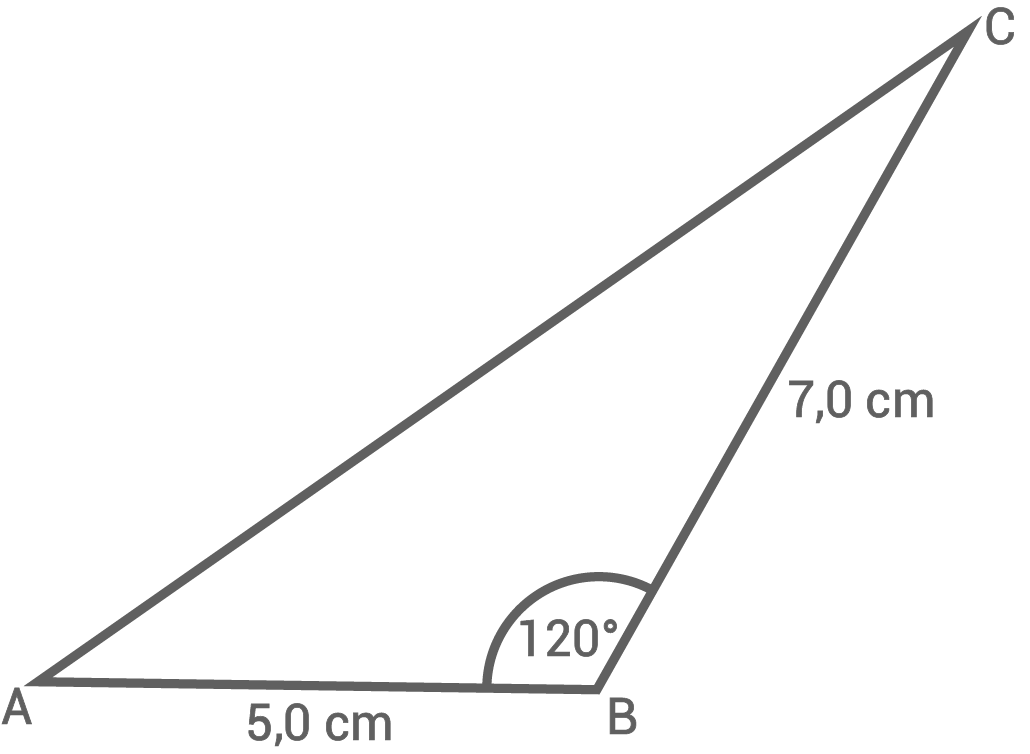Berechne die Länge der dritten Seite und die Größe der fehlenden Winkel.
Skizze nicht maßstäblich
5 BE
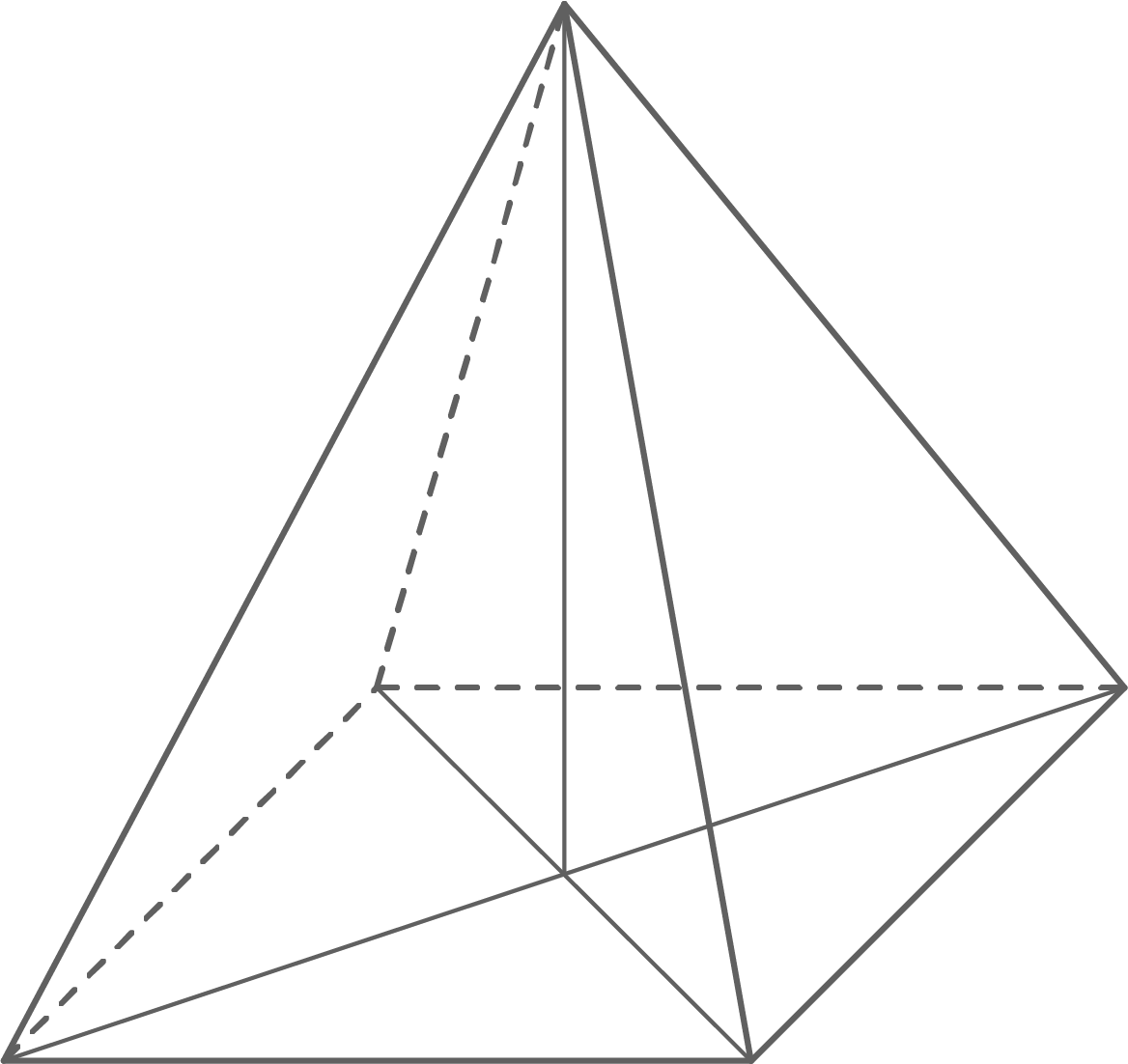
8
Das Zweitafelbild zeigt einen Körper im Maßstab 1:2.
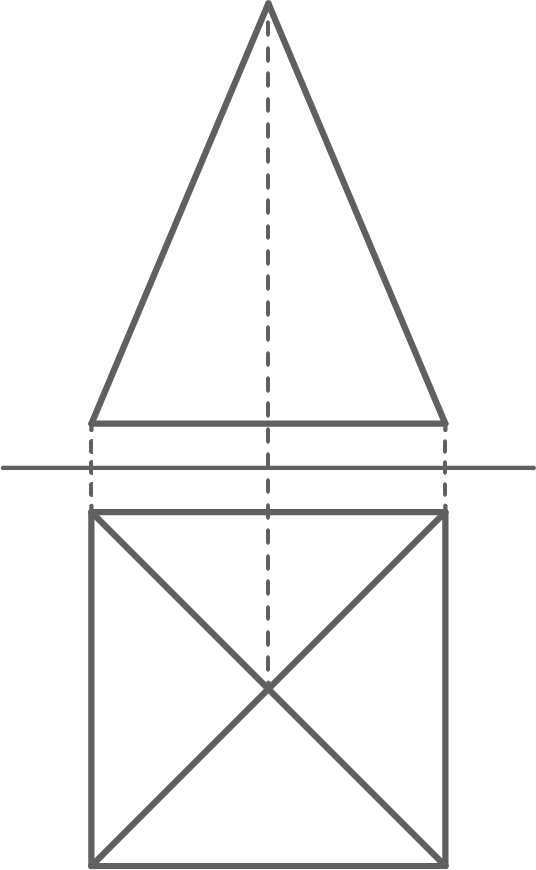
a)
Stelle den Körper auf unliniertem Papier in Originalgröße im Schrägbild dar.
4 BE
b)
Ermittle den Oberflächeninhalt des Körpers.
3 BE
2
a)
Lösung mit der Lösungsformel
![\(\begin{array}[t]{rll}
p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt]
p\,\%&=& \dfrac{1,99\,€}{0,99\,€}\cdot 100\,\% \\[5pt]
p\,\%&\approx& 201\,\%
\end{array}\)](https://mathjax.schullv.de/f35474e88fa6c4cc3506c36be5598a561d1ae2cc5f86b7b72e1346487c6cee42?color=5a5a5a)
Lösung mit Dreisatz
![\(\begin{array}{rcl}
0,99\,€& \mathrel{\widehat{=}}& 100\,\%\\[5pt]
0,01\,€ & \mathrel{\widehat{=}}& \dfrac{100}{99}\,\%\\[5pt]
1,99\,€ & \mathrel{\widehat{\approx}}& 201\,\%\,€
\end{array}\)](https://mathjax.schullv.de/ac17968af549acdc5798fb09cc85e01b90de0d64fc9c16c125a2ec37cf6c0648?color=5a5a5a)
Der Preis für ein Stück Butter stieg von Januar bis August auf 201 %.
b)
Lösung mit der Lösungsformel
![\(\begin{array}[t]{rll}
p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt]
p\,\%&=& \dfrac{0,44\,€}{1,99\,€}\cdot 100\,\% \\[5pt]
p\,\%&\approx& 22,1\,\%
\end{array}\)](https://mathjax.schullv.de/dbd77846797d72ebda87ea028014b4f2608091e4b181202e3d52d320dc5d67ed?color=5a5a5a)
Lösung mit Dreisatz
Der Preis ist um 
gesunken.
![\(\begin{array}{rcl}
1,99\,€& \mathrel{\widehat{=}}& 100\,\%\\[5pt]
0,01\,€ & \mathrel{\widehat{=}}& \dfrac{100}{199}\,\%\\[5pt]
0,44\,€ & \mathrel{\widehat{\approx}}& 22,1\,\%\,€
\end{array}\)](https://mathjax.schullv.de/00655fca3436860827a93e3880158e2fdd002ec643470ede4314ed94aacd5a76?color=5a5a5a)
Der Preis sank von August bis Dezember um 22,1 %.
3
4
Folgende Größen lassen sich aus dem Bild abmessen:
Höhe des Mannes: 
Durchmesser der Kugel:
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Die Größe des Mannes wird auf ungefähr 
geschätzt. Für den tatsächlichen Durchmesser der Kugel folgt damit:
Die Kugel hat also ungefähr einen Durchmesser von 
und damit einen Radius von 
Es ergibt sich folgendes Volumen:
![\(\begin{array}[t]{rll}
V&=& \dfrac{4}{3}\cdot \pi\cdot r^3 \\[5pt]
&=& \dfrac{4}{3}\cdot \pi\cdot (2,35\,\text{m})^3 \\[5pt]
&\approx& 54,4\,\text{m}^3 \\[5pt]
&\approx& 54\,400\,000\,\text{cm}^3
\end{array}\)](https://mathjax.schullv.de/a86b3a4e49a6d765ac5e089e223e59e62c106be10658276ad11f56dcd1001ad4?color=5a5a5a)
Wäre die Kugel vollständig mit Kunststoff gefüllt, so würde sich mit der Dichte 
die folgende Masse ergeben:
Masse in Tonnen: 
Wegen 
muss die Kugel einen Hohlraum haben.
Durchmesser der Kugel:
5
a)
Bei der Funktion handelt es sich um eine verschobene Normalparabel. Um diese grafisch darstellen zu können, wird der Scheitelpunkt berechnet:
Es gilt 
und 
b)
Die Nullstellen können mit der Lösungsformel berechnet werden.
![\(\begin{array}[t]{rll}
f(x) &=& 0 \\[5pt]
x^2 -6x +8 &=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/14e730aebb9e66d89799dbe15af7f874a2e11f0a940524a00f673702977fe40f?color=5a5a5a)
Es gilt und
![\(\begin{array}[t]{rll}
x_{1/2} &=& -\dfrac{p}{2}\pm \sqrt{\left(\dfrac{p}{2} \right)^2 -q} \\[5pt]
&=& -\dfrac{-6}{2}\pm \sqrt{\left(\dfrac{-6}{2} \right)^2 -8} \\[5pt]
&=& 3 \pm 1 \\[5pt]
x_1 &=& 2 \\[5pt]
x_2 &=& 4
\end{array}\)](https://mathjax.schullv.de/238536178eb7cfd84de8f604e98d98cc7c3fa42b51a620c0e319265d82bd6b1e?color=5a5a5a)
Die Nullstellen von sind 
und 
6
a)
Gesamtzahl der Schachteln: 
Anzahl der Schachteln mit weniger als 38 Hölzern:
Ereignis 
„Die entnommene Schachtel hat weniger als 38 Hölzer.“
Die Wahrscheinlichkeit, dass die ausgewählte Schachtel weniger als 38 Hölzer hat, ist 
Anzahl der Schachteln mit weniger als 38 Hölzern:
b)
c)
Die Gesamtzahl der Schachteln beträgt 55. Der Median ist daher durch den 28. Messwert bei aufsteigender Auflistung gegeben.
Der Median für die Anzahl der Hölzer je Schachtel ist 
7
Länge der dritten Seite berechnen
Mit dem Kosinussatz folgt für die fehlende Seitenlänge:
Die dritte Seite ist ca. 
lang.
Größe der fehlenden Winkel berechnen
Der Winkel 
kann mit dem Sinussatz berechnet werden:
![\(\begin{array}[t]{rll}
\dfrac{\overline{AC}}{\sin 120^{\circ}} &=& \dfrac{\overline{BC}}{\sin \alpha}\quad \scriptsize \mid\; \cdot \sin \alpha\\[5pt]
\dfrac{\overline{AC}}{\sin 120^{\circ}}\cdot \sin \alpha &=& \overline{BC}\quad \scriptsize \mid\;:\dfrac{\overline{AC}}{\sin 120^{\circ}} \\[5pt]
\sin \alpha &=& \overline{BC} \cdot \dfrac{\sin 120^{\circ}}{\overline{AC}} \\[5pt]
\sin \alpha &=& 7,0\,\text{cm} \cdot \dfrac{\sin 120^{\circ}}{10,4\,\text{cm}} \quad \scriptsize \mid\;\sin^{-1} \\[5pt]
\alpha &\approx& 35,7^{\circ}
\end{array}\)](https://mathjax.schullv.de/30e2dfd55347e8e78c6a655dad1c7ae386b2e2cca6d6ace244d3947bd2dfe68e?color=5a5a5a)
Für den dritten Winkel 
folgt mit der Innenwinkelsumme eines Dreiecks:
Die beiden fehlenden Winkel sind ca. 
und 
groß.
8
a)
Folgende Werte können gemessen werden:
Grundkante 
Höhe
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Mit dem Maßstab 1:2 ergeben sich die folgenden Werte:
Höhe
b)
Es handelt sich um eine gerade quadratische Pyramide mit folgenden Maßen:
Kantenlänge der Grundfläche: 
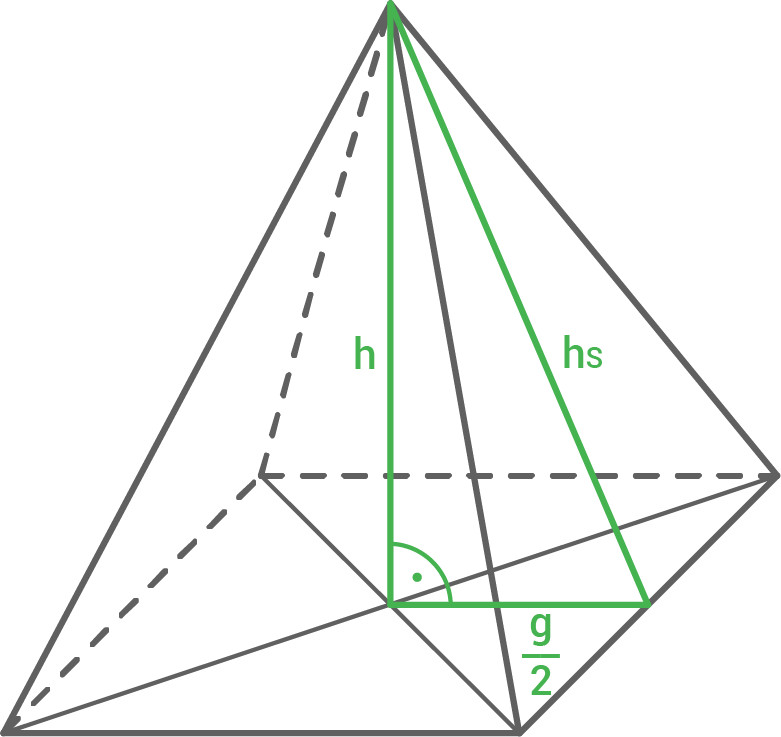Höhe:
Höhe 
der Seitenflächen mit dem Satz des Pythagoras berechnen:
![\(\begin{array}[t]{rll}
h_S^2 &=& \left(\dfrac{g}{2}\right)^2 + h^2 \\[5pt]
h_S^2 &=& (3\,\text{cm})^2 + (7\,\text{cm})^2 \\[5pt]
h_S^2 &=& 58\,\text{cm}^2 \quad \scriptsize \mid\;\sqrt{\,}\\[5pt]
h_S &\approx& 7,6\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/4d7693bcb99d1c840b055f1086e36069f1b5d6be22b1a0849afc5c04b9026c37?color=5a5a5a)
Flächeninhalt einer dreieckigen Seitenfläche berechnen:
![\(\begin{array}[t]{rll}
A_S&=& \dfrac{h_S\cdot g}{2} \\[5pt]
&=& \dfrac{7,6\,\text{cm}\cdot 6\,\text{cm}}{2} \\[5pt]
&=& 22,8\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/6416a7e99dd952c6909389b4640802012e6ca4c66950c28f22fd9cda535bb478?color=5a5a5a)
Flächeninhalt der quadratischen Grundfläche berechnen:
![\(\begin{array}[t]{rll}
A_G&=& (6\,\text{cm})^2 \\[5pt]
&=& 36\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/f5995f2c4c63744d03aee58b0fe2d40e918107a1017284019b2f92a4052e8a29?color=5a5a5a)
Für den Oberflächeninhalt der Pyramide ergibt sich insgesamt:
![\(\begin{array}[t]{rll}
A &=& A_G+4\cdot A_S \\[5pt]
&=& 36\,\text{cm}^2 + 4\,\cdot 22,8\,\text{cm}^2 \\[5pt]
&=& 127,2\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/d235aa5e6f9e29fbebd1ca36526299249f47a7b398512752ef9e46642626240a?color=5a5a5a)
Der Oberflächeninhalt des Körpers beträgt 
Höhe: