Wahlaufgaben
9
Wahlaufgabe Arithmetik/Algebra
9.1
Auf einem Parkplatz stehen Autos und Motorräder.
Es gibt insgesamt 60 Fahrzeuge mit 150 Rädern. Ermittle die Anzahl der Autos und Motorräder.
Es gibt insgesamt 60 Fahrzeuge mit 150 Rädern. Ermittle die Anzahl der Autos und Motorräder.
4 BE
9.2
Der Flächeninhalt des Trapezes beträgt 
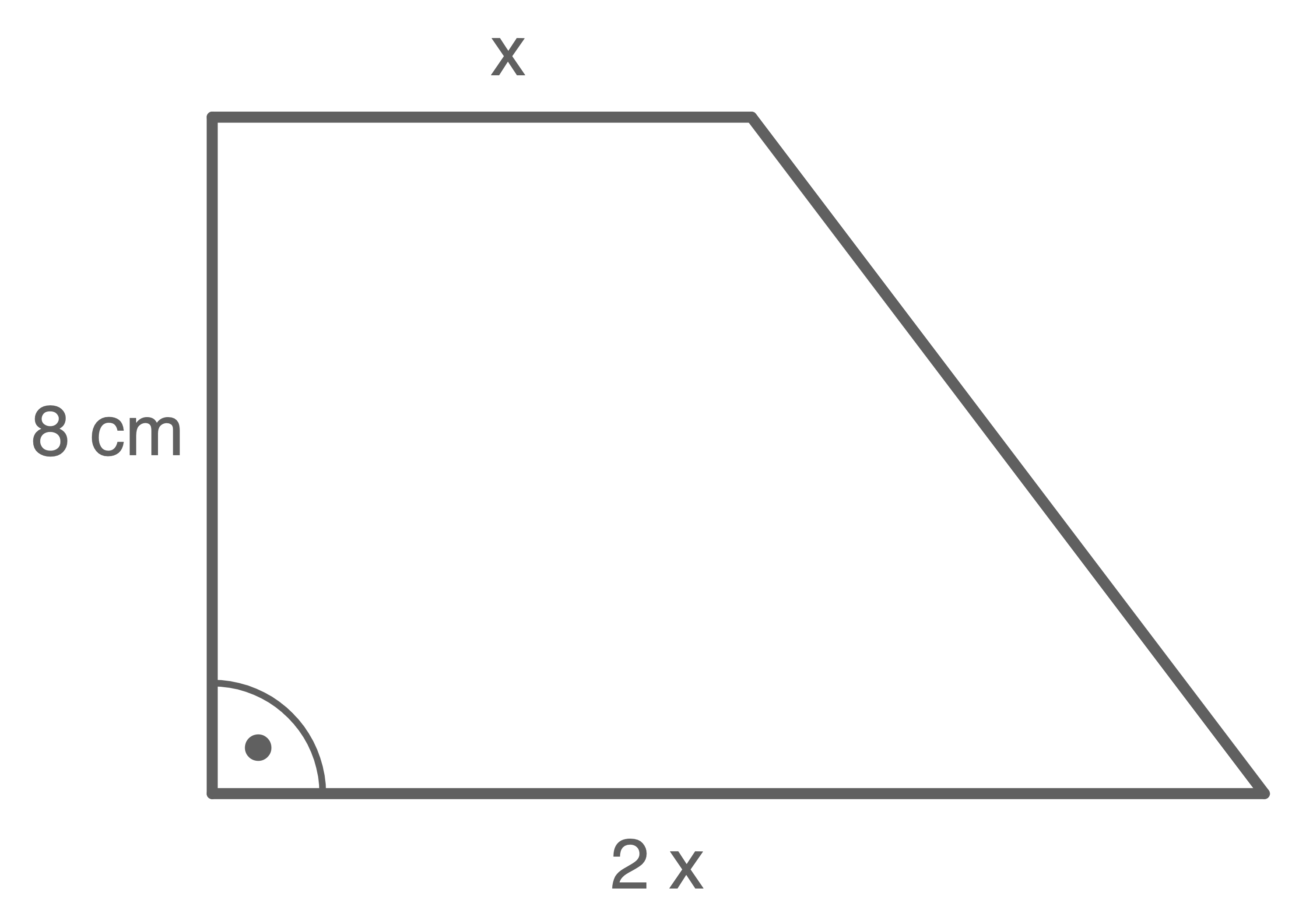 Ermittle die Seitenlänge
Ermittle die Seitenlänge 

Skizze nicht maßstäblich
3 BE
9.3
Am Ende einer Laufzeit von drei Jahren werden  bei einem Zinssatz von
bei einem Zinssatz von  ausgezahlt.
Berechne den Betrag in Euro, der zu Beginn der Laufzeit angelegt wurde.
ausgezahlt.
Berechne den Betrag in Euro, der zu Beginn der Laufzeit angelegt wurde.
3 BE
10
Wahlaufgabe Stochastik
10.1
Historische Münzen werden in gleichen Verpackungen gelagert.
Zwei Verpackungen enthalten Taler, eine Verpackung enthält Dukaten und drei Verpackungen enthalten Gulden. Es werden zufällig zwei Verpackungen ohne Zurücklegen ausgewählt. Entscheide, ob mit einer Wahrscheinlichkeit von mindestens 50 % die Münzen unterschiedlich sind.
Begründe deine Entscheidung rechnerisch mithilfe eines Baumdiagramms.
Zwei Verpackungen enthalten Taler, eine Verpackung enthält Dukaten und drei Verpackungen enthalten Gulden. Es werden zufällig zwei Verpackungen ohne Zurücklegen ausgewählt. Entscheide, ob mit einer Wahrscheinlichkeit von mindestens 50 % die Münzen unterschiedlich sind.
Begründe deine Entscheidung rechnerisch mithilfe eines Baumdiagramms.
5 BE
10.2
Beim Weitsprung wurden folgende Sprungweiten erreicht:
Von jeder Sportlerin wird jeweils der weiteste Sprung gewertet.
Berechne für die weitesten Sprünge das arithmetische Mittel.
| Sprungweite 1 | Sprungweite 2 | Sprungweite 3 | |
| Anni | 2,85 m | 3,15 m | 3,65 m |
| Britt | 4,20 m | 4,20 m | 4,15 m |
| Celine | 3,10 m | 3,05 m | 4,05 m |
| Diana | 4,10 m | 3,85 m | 3,95 m |
| Emma | 3,50 m | 3,60 m | 3,20 m |
3 BE
10.3
Ein zufälliges Ereignis hat eine Wahrscheinlichkeit von 40 %.
Beschreibe ein solches Ereignis für ein selbst gewähltes Zufallsexperiment.
2 BE
11
Wahlaufgabe Geometrie
11.1
Ein Hochmoor hat annähernd die Form eines Parallelogramms mit einer Fläche von 
Die Torfschicht dieses Hochmoors ist drei bis fünf Meter dick.
Die Torfschicht dieses Hochmoors ist drei bis fünf Meter dick.
a)
Berechne das Volumen des Torfs, das mindestens im Hochmoor lagert.
Eine Seite des Parallelogramms ist 280 m lang und ein Winkel hat eine Größe von 120°.
2 BE
b)
Berechne den Umfang des Parallelogramms.
3 BE
11.2
Die steile Treppe in der Silberkarklamm (Österreich) hat einen Anstiegswinkel von 60°.
Ein Modell dieser Treppe wurde im Maßstab 1:100 gebaut.
Die Treppe ist im Modell 50 cm lang.
Die Treppe ist im Modell 50 cm lang.
a)
Berechne den Höhenunterschied, den die Besucher mit dieser Treppe in der Silberkarklamm überwinden.
3 BE
b)
Berechne die Steigung der Treppe in Prozent.
2 BE
12
Wahlaufgabe Funktionen
12.1
Gegeben sind die Funktionen  und
und  mit
mit  Gib die Aussage an, die wahr ist.
A
Gib die Aussage an, die wahr ist.
A  Die Graphen beider Funktionen schneiden die
Die Graphen beider Funktionen schneiden die  -Achse im Punkt
-Achse im Punkt  B
B  Beide Funktionen haben die Nullstelle
Beide Funktionen haben die Nullstelle  C
C  Die Graphen beider Funktionen sind im gesamten Definitionsbereich steigend.
Die Graphen beider Funktionen sind im gesamten Definitionsbereich steigend.
1 BE
12.2
Durch die Gleichung  mit
mit  ist eine Funktion gegeben.
ist eine Funktion gegeben.
 ist eine weitere Funktion gegeben.
ist eine weitere Funktion gegeben.
a)
Skizziere den Graphen von  mindestens für
mindestens für  in ein Koordinatensystem.
in ein Koordinatensystem.
(1 Längeneinheit entspricht 1 Zentimeter)
Durch die Gleichung (1 Längeneinheit entspricht 1 Zentimeter)
3 BE
b)
Skizziere den Graphen der Funktion  in das Koordinatensystem von Aufgabe a).
in das Koordinatensystem von Aufgabe a).
2 BE
c)
Die Punkte  und
und  liegen auf dem Graphen der Funktion
liegen auf dem Graphen der Funktion  Gib die fehlenden Koordinaten der Punkte
Gib die fehlenden Koordinaten der Punkte  und
und  an.
an.
2 BE
d)
Die Graphen der Funktionen  und
und  schneiden sich in den Punkten
schneiden sich in den Punkten  und
und  Berechne die Länge der Strecke
Berechne die Länge der Strecke 
2 BE
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
9.1
| Autos | Motorräder | insgesamt | |
| Fahrzeuge | |||
| Räder |
9.2
Formel zur Berechnung des Flächeninhalts eines Trapezes: 
![\(\begin{array}[t]{rll}
72\,\text{cm}^2&=& \dfrac{2x+x}{2}\cdot 8 \,\text{cm} \quad \scriptsize \mid\; :8\,\text{cm} \\[5pt]
9\,\text{cm}&=& \dfrac{3x}{2} \quad \scriptsize \mid\;\cdot 2\\[5pt]
18\,\text{cm}&=& 3x \quad \scriptsize \mid\; : 3\\[5pt]
6 \,\text{cm}&=& x
\end{array}\)](https://mathjax.schullv.de/20f43298286605130f8129397054d8011729b9d7c823de409a025613fc416ad5?color=5a5a5a) Die Seitenlänge
Die Seitenlänge  beträgt
beträgt 
9.3
10.1
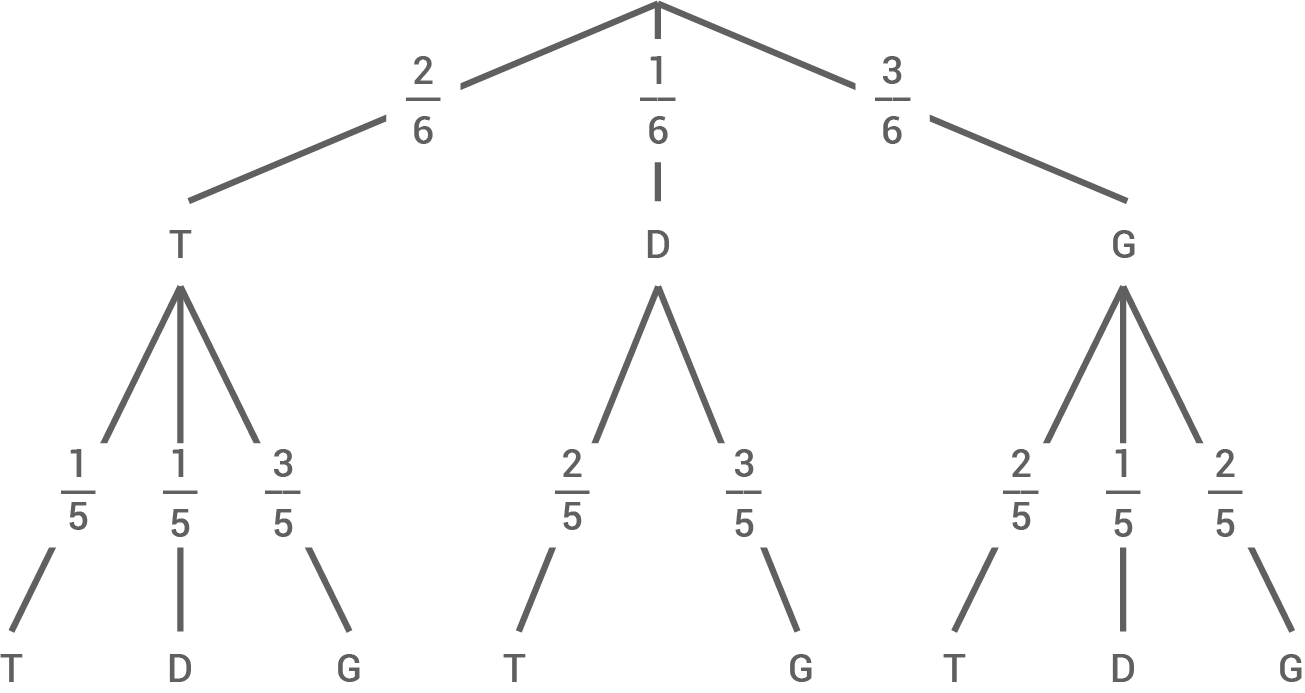
10.2
Weiteste Sprünge:
Damit lässt sich nun das arithmetische Mittel berechnen:
Das arithmetische Mittel für die weitesten Sprünge beträgt 3,92 m.
| Sprungweite 1 | Sprungweite 2 | Sprungweite 3 | |
| Anni | 2,85 m | 3,15 m | 3,65 m |
|---|---|---|---|
| Britt | 4,20 m | 4,20 m | 4,15 m |
| Celine | 3,10 m | 3,05 m | 4,05 m |
| Diana | 4,10 m | 3,85 m | 3,95 m |
| Emma | 3,50 m | 3,60 m | 3,20 m |
10.3
In einer Urne sind 4 blaue und 6 weiße Kugeln. Eine Kugel wird zufällig gezogen.
Ereignis  „Es wird eine blaue Kugel gezogen.“
„Es wird eine blaue Kugel gezogen.“

11.1
a)
Da die Torfschicht mindestens  dick ist, gilt
dick ist, gilt  Mit der Formel zur Berechnung des Volumens eines Prismas gilt:
Mit der Formel zur Berechnung des Volumens eines Prismas gilt:
![\(\begin{array}[t]{rll}
V&=& G\cdot h_{\,\text{Prisma}}&\quad \scriptsize \\[5pt]
&=& 120\;000\,\text{m}^2\cdot 3 \,\text{m} &\quad \scriptsize \\[5pt]
&=& 360\;000\,\text{m}^3
\end{array}\)](https://mathjax.schullv.de/b41501d56378ff2ad054b6c9dd0bebebd64ed48e67e7c14828f9d7679ccba87c?color=5a5a5a) Im Hochmoor lagern mindestens
Im Hochmoor lagern mindestens  Torf.
Torf.
b)
Durch die Angaben in der Aufgabenstellung lässt sich folgende Skizze erstellen:
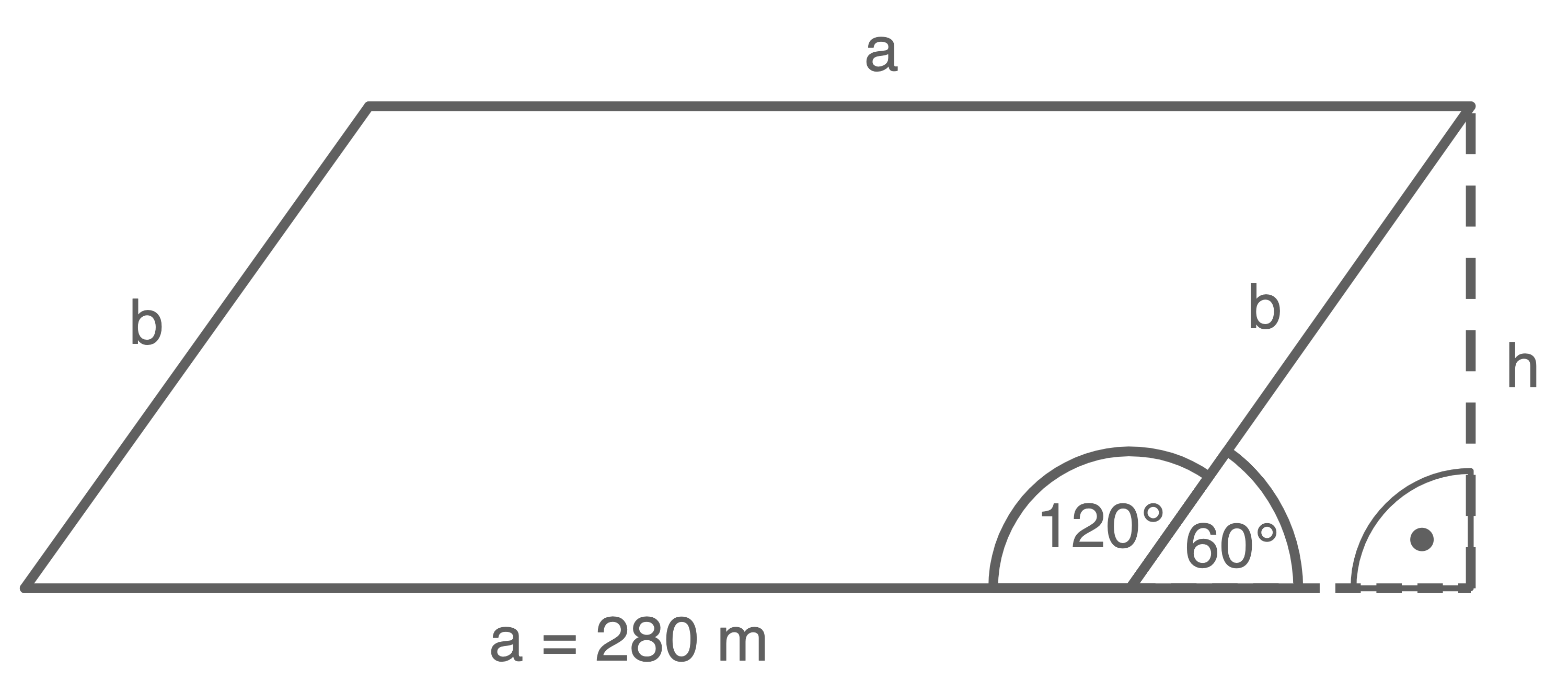 Die Höhe
Die Höhe  kann mit der Formel für den Flächeninhalt eines Parallelogramms bestimmt werden.
kann mit der Formel für den Flächeninhalt eines Parallelogramms bestimmt werden.
![\(\begin{array}[t]{rll}
A_{\text{Trapez}}&=&a\cdot h \quad \scriptsize \mid\;:a \\[5pt]
\dfrac{A_{\text{Trapez}}}{a} &=& h \\[5pt]
\dfrac{120\,000\,\text{m}^2}{280\,\text{m}}&=& h\\[5pt]
428,6\,\text{m}&\approx& h
\end{array}\)](https://mathjax.schullv.de/06740b56d7ec86e7af080fd756d1e800d40b14250c66bf1aef0d472cb6f1995f?color=5a5a5a) Die Länge der Strecke
Die Länge der Strecke  lässt sich mit dem Sinus berechnen.
lässt sich mit dem Sinus berechnen.
![\(\begin{array}[t]{rll}
\sin 60°&=&\dfrac{h}{b} \quad \scriptsize \mid\;\cdot b\\[5pt]
b\cdot \sin 60°&=& h \quad \scriptsize \mid\;:\sin 60°\\[5pt]
b&=&\dfrac{h}{\sin 60°} \\[5pt]
b&\approx&\dfrac{428,6\,\text{m}}{\sin(60^{\circ})} \\[5pt]
b&\approx& 494,9\,\text{m}
\end{array}\)](https://mathjax.schullv.de/0888513ebf8e248c7827b6ddc34408764d9c27964d667eeead49189e04552069?color=5a5a5a) Für den Umfang des Parallelogramms ergibt sich schließlich:
Für den Umfang des Parallelogramms ergibt sich schließlich:
![\(\begin{array}[t]{rll}
u&=& 2\cdot (a+b) \\[5pt]
&=& 2\cdot (280\,\text{m}+494,9\,\text{m}) \\[5pt]
&\approx& 1\,550 \,\text{m}
\end{array}\)](https://mathjax.schullv.de/a908144b95759bf9c3823e129fed6c44afe433db2de7b02db818282edc7d3b9f?color=5a5a5a) Das Parallelogramm hat ungefähr einen Umfang von
Das Parallelogramm hat ungefähr einen Umfang von 

11.2
a)
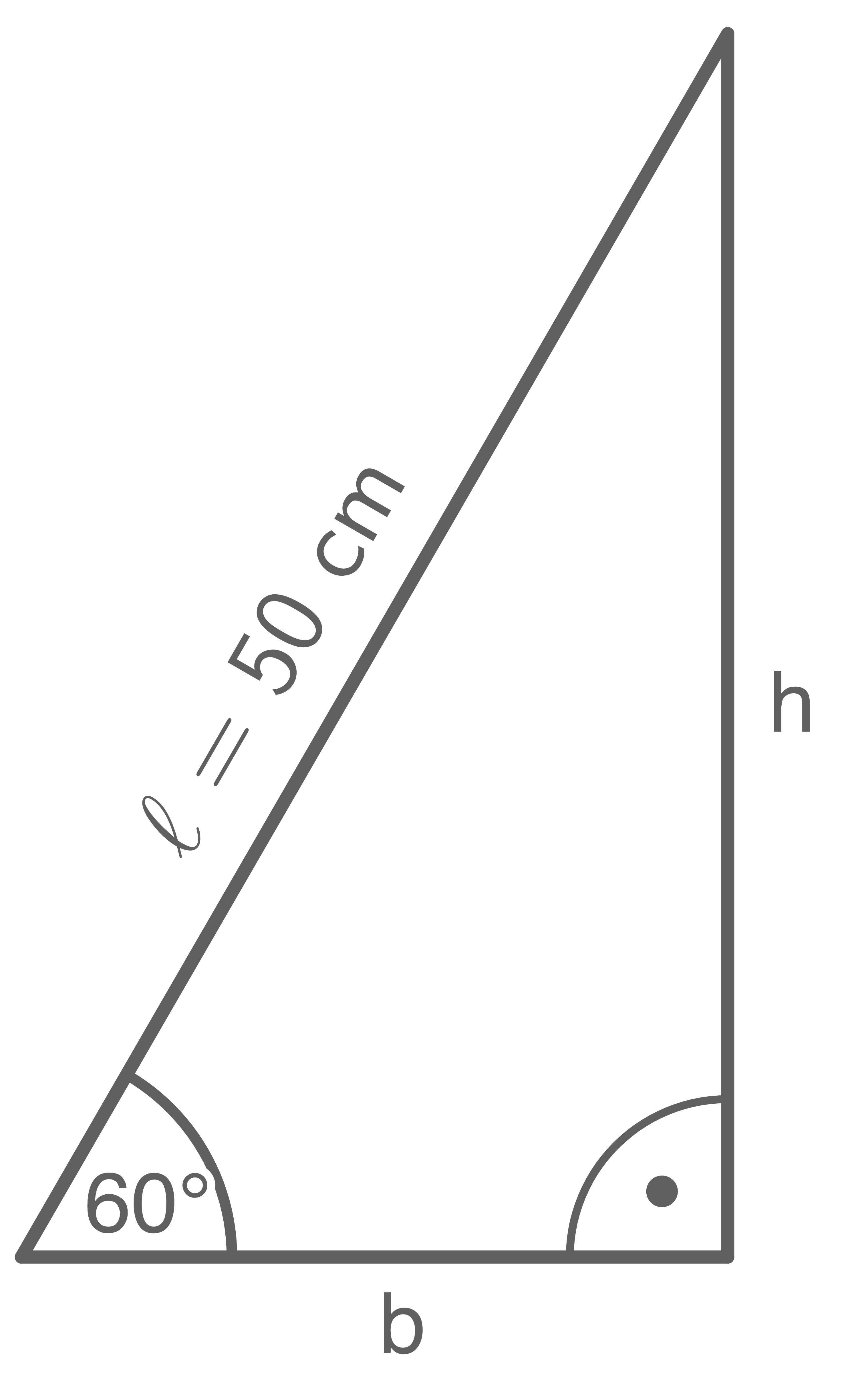
Höhe der Treppe im Modell berechnen:
![\(\begin{array}[t]{rll}
\sin(60^{\circ} )&=& \dfrac{h}{50\,\text{cm} } \quad \scriptsize \mid\; \cdot 50\,\text{cm}\\[5pt]
\sin(60^{\circ}) \cdot 50\,\text{cm}&=& h \\[5pt]
43,30 \,\text{cm} &\approx& h
\end{array}\)](https://mathjax.schullv.de/342ce5499316133f336a895ac57104326dd804b38ed99cafb0af40049c665613?color=5a5a5a) Berechnung der tatsächlichen Höhe
Berechnung der tatsächlichen Höhe  der Treppe mit dem Maßstab:
der Treppe mit dem Maßstab:
![\(\begin{array}[t]{rll}
\dfrac{1}{100}&=& \dfrac{43,3\,\text{cm}}{h_T} \quad \scriptsize \mid\; \cdot h_T \\[5pt]
\dfrac{h_T}{100}&=& 43,3\,\text{cm} \quad \scriptsize \mid\; \cdot 100 \\[5pt]
h_T&=& 43\,300\,\text{cm} \\[5pt]
h_T&=& 43,3 \,\text{m}
\end{array}\)](https://mathjax.schullv.de/fa116150459501d27cc4d93ae6aad83bc9b6c8f15c0359c52aad2903630416d8?color=5a5a5a)
Die Besucher überwinden einen Höhenunterschied von
b)
Die Steigung  ergibt sich aus dem Quotienten der Höhe
ergibt sich aus dem Quotienten der Höhe  und der Breite
und der Breite 
![\(\begin{array}[t]{rll}
\tan 60°&=& \dfrac{h}{b} \\[5pt]
\tan 60°&=& m \\[5pt]
1,732&\approx& m \\[5pt]
173,2\,\%&\approx& m \\[5pt]
\end{array}\)](https://mathjax.schullv.de/170b7a77c7e7c3c96c1192084ae1069ba3515ea07a942309da566a4ffd553828?color=5a5a5a) Die Treppe hat ungefähr eine Steigung von
Die Treppe hat ungefähr eine Steigung von 
12.1
Aussage A überprüfen

 Die Aussage stimmt also nicht.
Aussage B überprüfen
Die Aussage stimmt also nicht.
Aussage B überprüfen
![\(\begin{array}[t]{rll}
f(x)&=& 0 \\[5pt]
x+3&=& 0 \quad \scriptsize \mid\;-3 \\[5pt]
x&=& -3
\end{array}\)](https://mathjax.schullv.de/81b304dff522106e9f96e4d1ed6cb21e9448bdb27f1dc6cd0bd026a46bc9fe99?color=5a5a5a)
![\(\begin{array}[t]{rll}
g(x)&=& 0 \\[5pt]
x^2+2x-3&=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/cb050ceeb34ab0f645cc23585e4336330c2406ddf36d20ca3ffb1a1324ac2acf?color=5a5a5a) Es gilt
Es gilt  und
und  Mit der Lösungsformel folgt:
Mit der Lösungsformel folgt:
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
x_{1/2}&=& -\dfrac{2}{2}\pm\sqrt{\left(\dfrac{2}{2}\right)^2-(-3)} \\[5pt]
x_{1/2}&=& -1\pm\sqrt{4}\\[5pt]
x_1&=&-1+2=1\\[5pt]
x_2&=&-1-2=-3\\[5pt]
\end{array}\)](https://mathjax.schullv.de/8f462561f976c113f103333d96b43f8c294d0ee782fe312cb8f6040c56ce1f6d?color=5a5a5a) Somit stimmt die Aussage.
Aussage C überprüfen
Die Aussage stimmt nicht, denn bei
Somit stimmt die Aussage.
Aussage C überprüfen
Die Aussage stimmt nicht, denn bei  handelt es sich um eine Parabel. Diese kann nicht im gesamten Definitionsbereich steigend sein.
handelt es sich um eine Parabel. Diese kann nicht im gesamten Definitionsbereich steigend sein.
12.2
a)
| -2 | -8 |
| -1,5 | -3,375 |
| -1 | -1 |
| -0,5 | -0,125 |
| 0 | 0 |
| 0,5 | 0,125 |
| 1 | 1 |
| 1,5 | 3,375 |
| 2 | 8 |
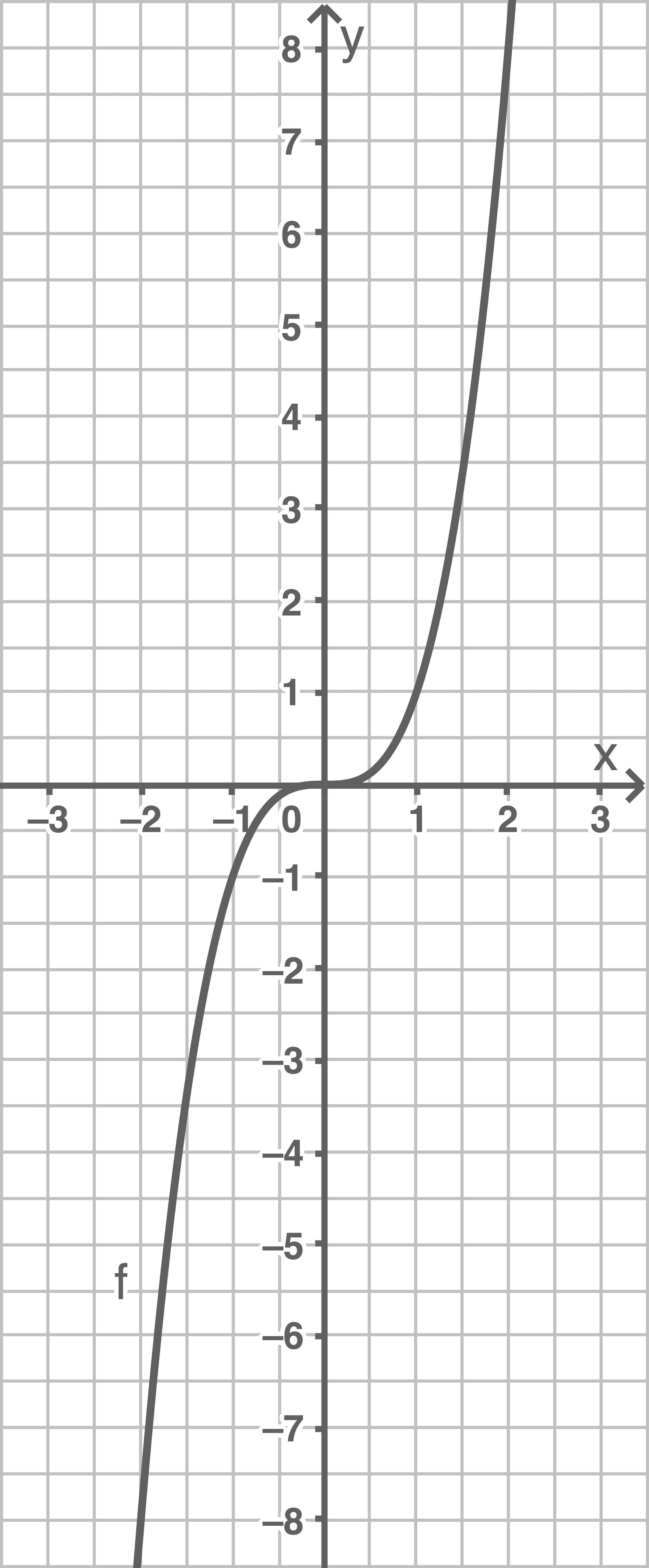
b)
| -3 | -0,33 |
| -2 | -0,5 |
| -1 | -1 |
| -0,5 | -2 |
| 0,5 | 2 |
| 1 | 1 |
| 2 | 0,5 |
| 3 | 0,33 |
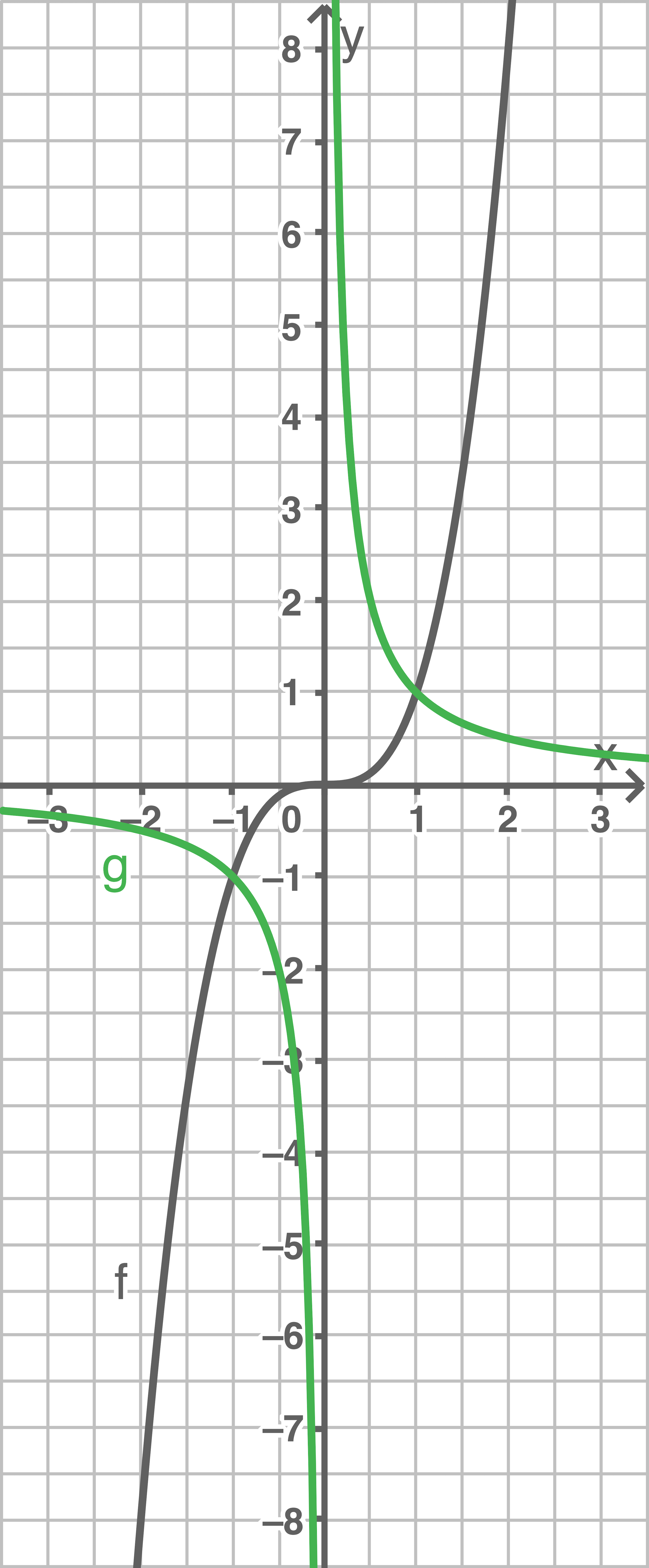
c)
Es wird in beiden Fällen die bekannte Koordinate in die Funktionsgleichung eingesetzt und nach der unbekannten Variable umgestellt.
![\(\begin{array}[t]{rll}
100&=& \dfrac{1}{x} &\quad \scriptsize \mid\; \cdot x\\[5pt]
100\cdot x&=& 1 &\quad \scriptsize \mid\; :100\\[5pt]
x&=& 0,01
\end{array}\)](https://mathjax.schullv.de/2fd69899dde3c3b29826a3a5a243c34ec679bcae05f04343ddb2a5184dee6c91?color=5a5a5a) Somit gilt:
Somit gilt: 
![\(\begin{array}[t]{rll}
y&=& \dfrac{1}{-0,5} &\\[5pt]
y&=& -2
\end{array}\)](https://mathjax.schullv.de/e5ea123b3f2c31497551e802afa1b4f5696be5a02b771b720f8dd35ed488639f?color=5a5a5a) Somit gilt:
Somit gilt: 
d)
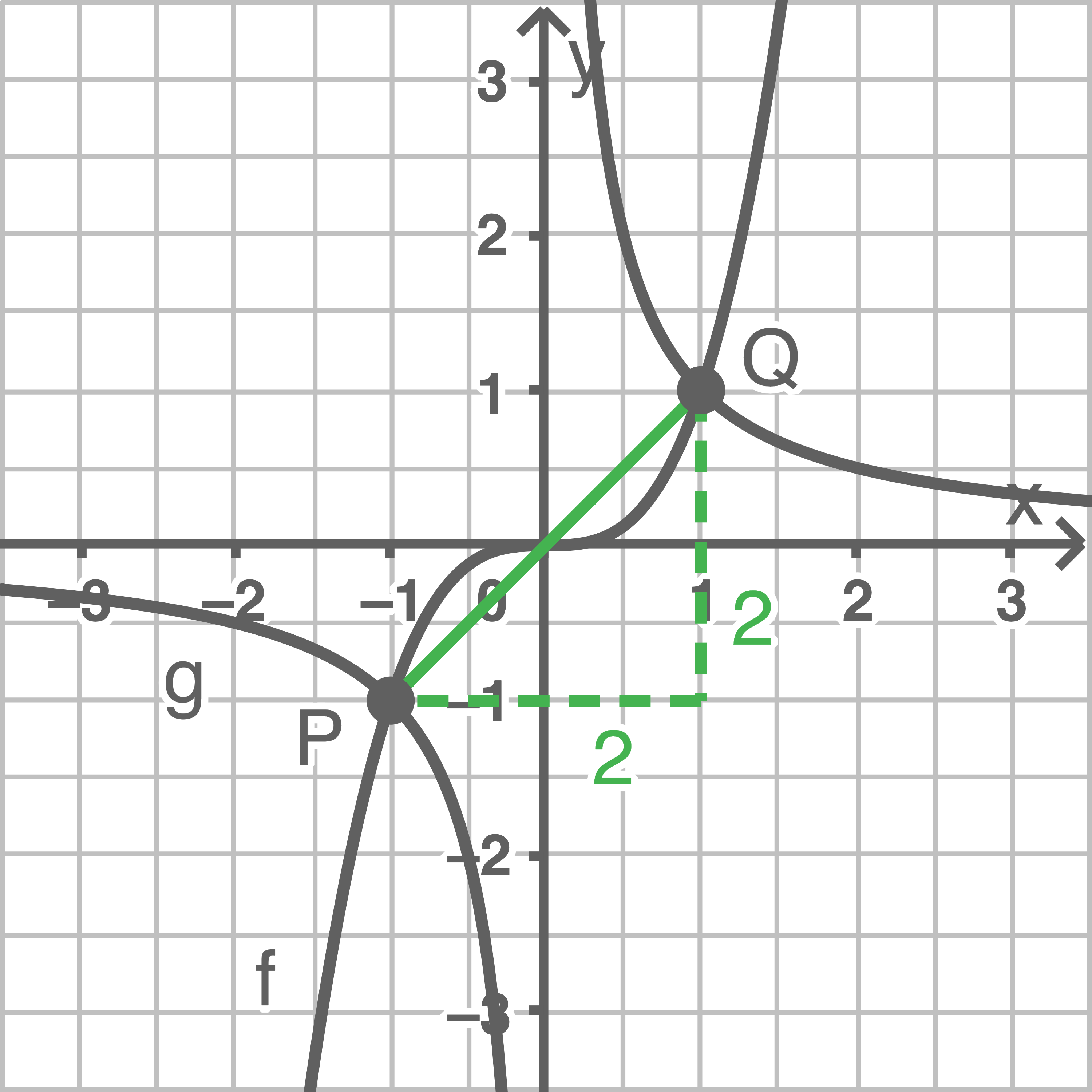
Mit dem Satz des Pythagoras gilt:
![\(\begin{array}[t]{rll}
\overline{PQ}^2&=& (2 \,\text{cm})^2+ (2\,\text{cm})^2 \quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
\overline{PQ}&=& \sqrt{(2 \,\text{cm})^2+ 2(\,\text{cm})^2} \\[5pt]
\overline{PQ}&=& \sqrt{8\,\text{cm}^2} \\[5pt]
\overline{PQ}&\approx& 2,8 \,\text{cm}
\end{array}\)](https://mathjax.schullv.de/20a8f0843fefbb2778ee2017c482a8fda5bf7b2ff2fd904b8069ef272da8bd75?color=5a5a5a) Die Strecke
Die Strecke  ist ungefähr
ist ungefähr  lang.
lang.