Wahlaufgaben
9
Wahlaufgabe Funktionen
9.1
In einem Koordinatensystem sind die Punkte  ,
,  und
und  gegeben.
gegeben.
Einer dieser Punkte ist der Scheitelpunkt einer verschobenen Normalparabel.
Durch die beiden anderen Punkte verläuft der Graph einer linearen Funktion. Dieser ist monoton fallend.
Einer dieser Punkte ist der Scheitelpunkt einer verschobenen Normalparabel.
Durch die beiden anderen Punkte verläuft der Graph einer linearen Funktion. Dieser ist monoton fallend.
a)
Stelle diesen Sachverhalt graphisch dar.
4 BE
b)
Gib die zur Darstellung zugehörigen Funktionsgleichungen an.
2 BE
9.2
Eine Silvesterrakete wird gestartet. Ihre Flugbahn lässt sich vereinfacht durch 
 mathematisch beschreiben.
mathematisch beschreiben.
(Eine Längeneinheit entspricht einem Meter.)
(Eine Längeneinheit entspricht einem Meter.)
a)
Gib die maximale Höhe der Flugbahn der Rakete an.
1 BE
b)
Berechne die Entfernung zwischen Start- und Landepunkt.
3 BE
10
Wahlaufgabe Stochastik
10.1
In einer theoretischen Führerscheinprüfung werden je Fragestellung drei Antworten vorgegeben. Eine davon ist richtig. Eine Teilnehmerin kreuzt bei zwei Fragen jeweils eine Möglichkeit zufällig an.
Ein Teilnehmer kreuzt zwei Antworten zufällig an.
a)
Berechne die Wahrscheinlichkeit dafür, dass beide Entscheidungen richtig sind.
Bei einer anderen Frage sind zwei von drei Antworten richtig.
2 BE
Ein Teilnehmer kreuzt zwei Antworten zufällig an.
b)
Ermittle die Wahrscheinlichkeit dafür, dass seine Entscheidung richtig ist.
2 BE
10.2
Im Kreisdiagramm ist das Ergebnis einer Schülerbefragung zum Stand ihrer Bewerbung dargestellt.
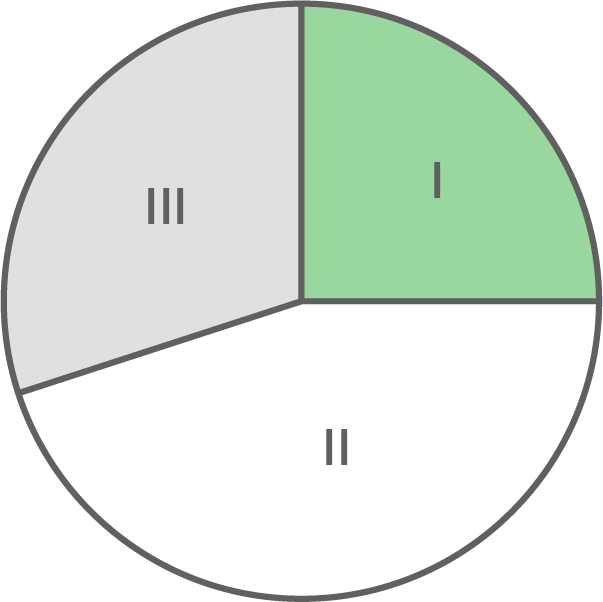
 der Befragten haben noch keine Vorstellung von ihrem späteren Beruf.
der Befragten haben noch keine Vorstellung von ihrem späteren Beruf.
 der Befragten haben klare Vorstellungen von ihrem späteren Beruf, aber noch keine Bewerbung abgeschickt.
der Befragten haben klare Vorstellungen von ihrem späteren Beruf, aber noch keine Bewerbung abgeschickt.

I
II
III
66 Befragte haben schon Bewerbungen abgeschickt.
Berechne die Anzahl der Befragten.
3 BE
10.3
In einem Behälter befinden sich fünf blaue, drei rote und zwei gelbe Kugeln. Es werden zufällig zwei Kugeln ohne Zurücklegen gezogen.
Beschreibe dafür ein Ereignis mit einer Wahrscheinlichkeit von und stelle diesen Sachverhalt in einem zugehörigen Baumdiagramm dar.
und stelle diesen Sachverhalt in einem zugehörigen Baumdiagramm dar.
Beschreibe dafür ein Ereignis mit einer Wahrscheinlichkeit von
3 BE
11
Wahlaufgabe Arithmetik/Algebra
11.1
Jens und Uwe kaufen für ihre Familien Tickets für dasselbe Konzert. Jens bezahlt für fünf Karten der Preiskategorie I und für drei der Preiskategorie III insgesamt 251,00 Uwe bezahlt für sechs Tickets der Preiskategorie I und für zwei der Preiskategorie III insgesamt 234,00
Uwe bezahlt für sechs Tickets der Preiskategorie I und für zwei der Preiskategorie III insgesamt 234,00 .
Ermittle die fehlenden Preise:
.
Ermittle die fehlenden Preise:
| Preiskategorie | |||
|---|---|---|---|
| Preis | ... | ... |
4 BE
11.2
Die Bank hat Frau Marx einen Überziehungskredit gewährt.
Der Jahreszinssatz beträgt dafür 11,5 %. Frau Marx überzieht ihr Konto um 640,00 Berechne die Zinsen, die Frau Marx für 25 Tage bezahlen muss.
Berechne die Zinsen, die Frau Marx für 25 Tage bezahlen muss.
Der Jahreszinssatz beträgt dafür 11,5 %. Frau Marx überzieht ihr Konto um 640,00
2 BE
11.3
Gegeben sind die Terme  und
und 


a)
Berechne den Wert eines Terms für  und
und  .
.
1 BE
b)
Weise durch Umformen eines Terms nach, dass gilt:
Term = Term
= Term 
Term
3 BE
12
Wahlaufgabe Geometrie
12.1
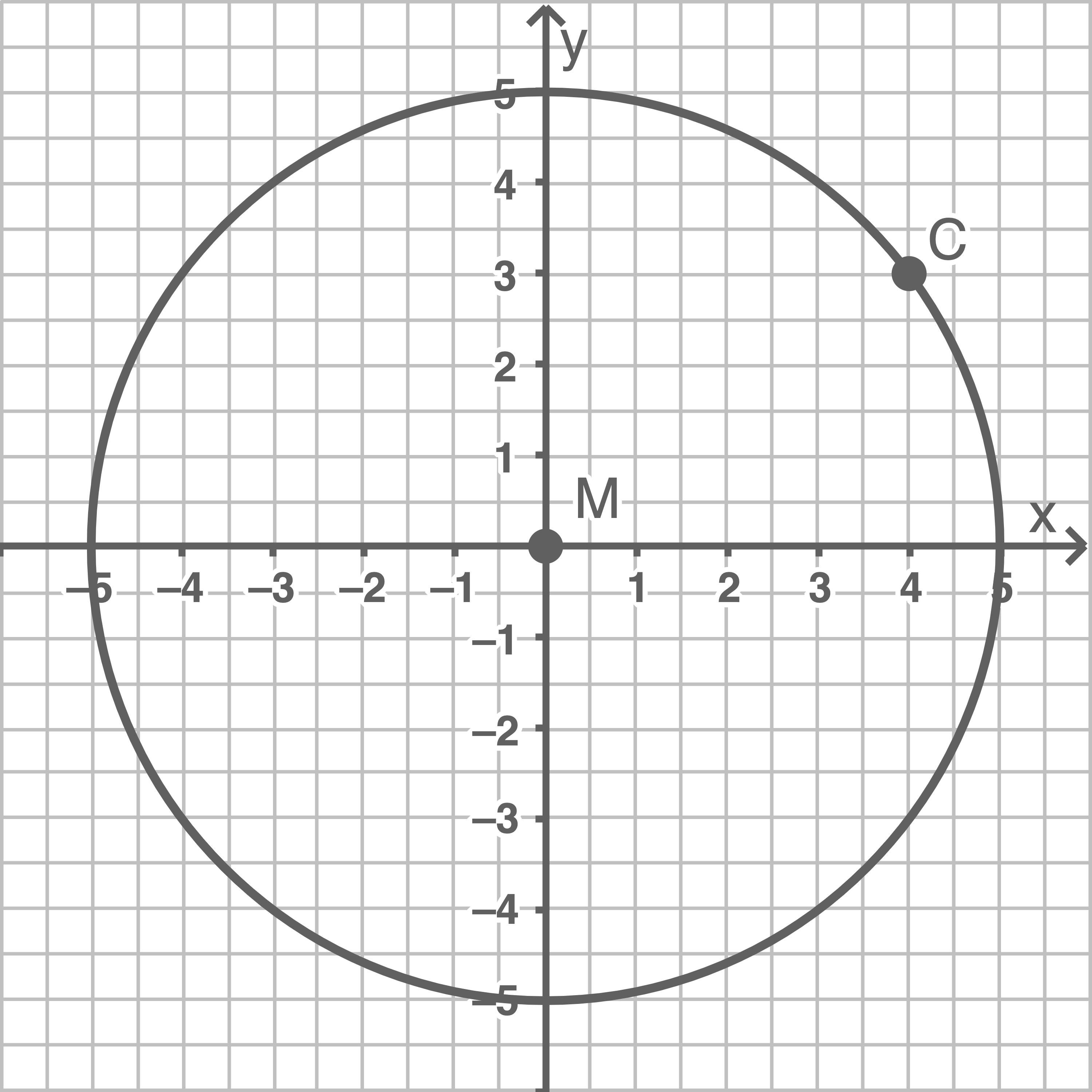
Ein Kreis im Koordinatensystem mit dem Mittelpunkt  hat einen Durchmesser von 10 cm. Der Punkt
hat einen Durchmesser von 10 cm. Der Punkt  liegt auf dem Kreis.
liegt auf dem Kreis.
(Eine Längeneinheit entspricht einem Zentimeter.) -Achse und der Punkt C bilden ein Dreieck.
-Achse und der Punkt C bilden ein Dreieck.
(Eine Längeneinheit entspricht einem Zentimeter.)
a)
Stelle den Sachverhalt auf kariertem Papier dar.
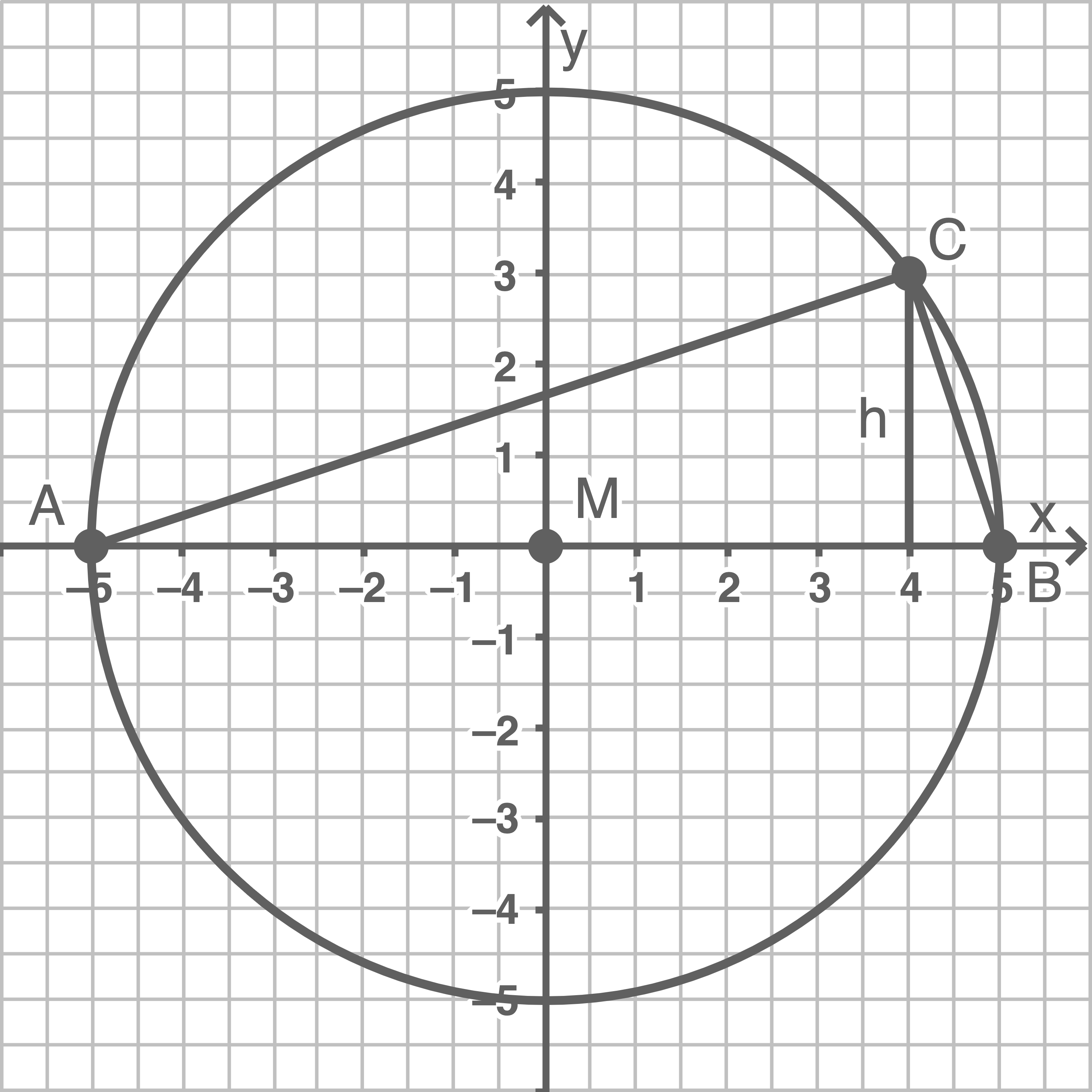
Die beiden Schnittpunkte des Kreises mit der
2 BE
b)
Berechne den Flächeninhalt des Dreiecks.
2 BE
c)
Begründe, dass der Innenwinkel am Punkt C ein rechter Winkel ist.
2 BE
12.2
Die neue Zugspitzbahn beginnt an der Talstation auf einer Höhe von  ü. NN und endet an der Bergstation auf
ü. NN und endet an der Bergstation auf  ü. NN. Auf einer Wanderkarte mit dem Maßstab
ü. NN. Auf einer Wanderkarte mit dem Maßstab  haben beide Stationen den Abstand
haben beide Stationen den Abstand  Berechne den durchschnittlichen Anstiegswinkel der Zugspitzbahn.
Berechne den durchschnittlichen Anstiegswinkel der Zugspitzbahn.
4 BE
9.1
a)
Möglichkeit 1:
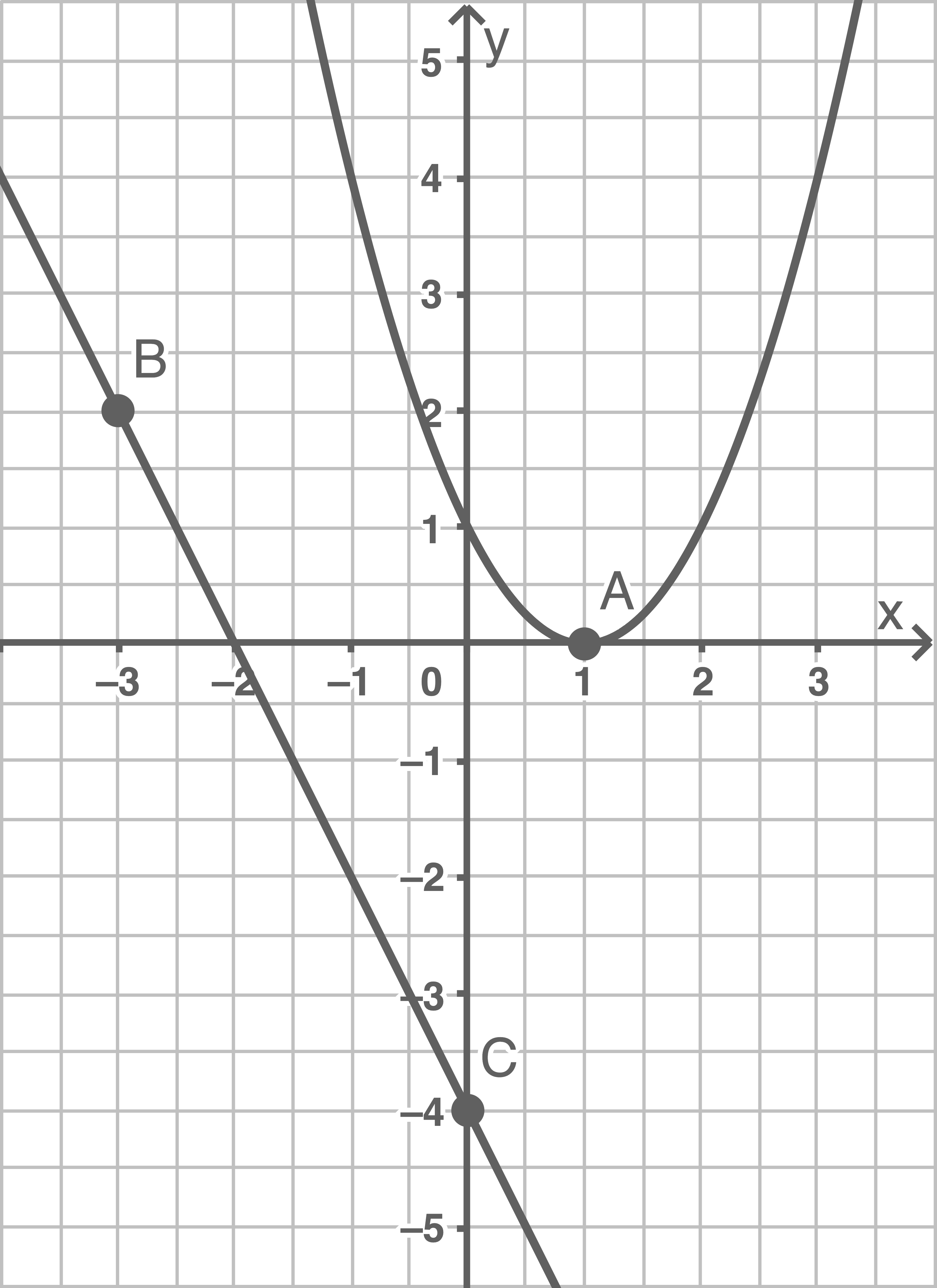

Möglichkeit 2:
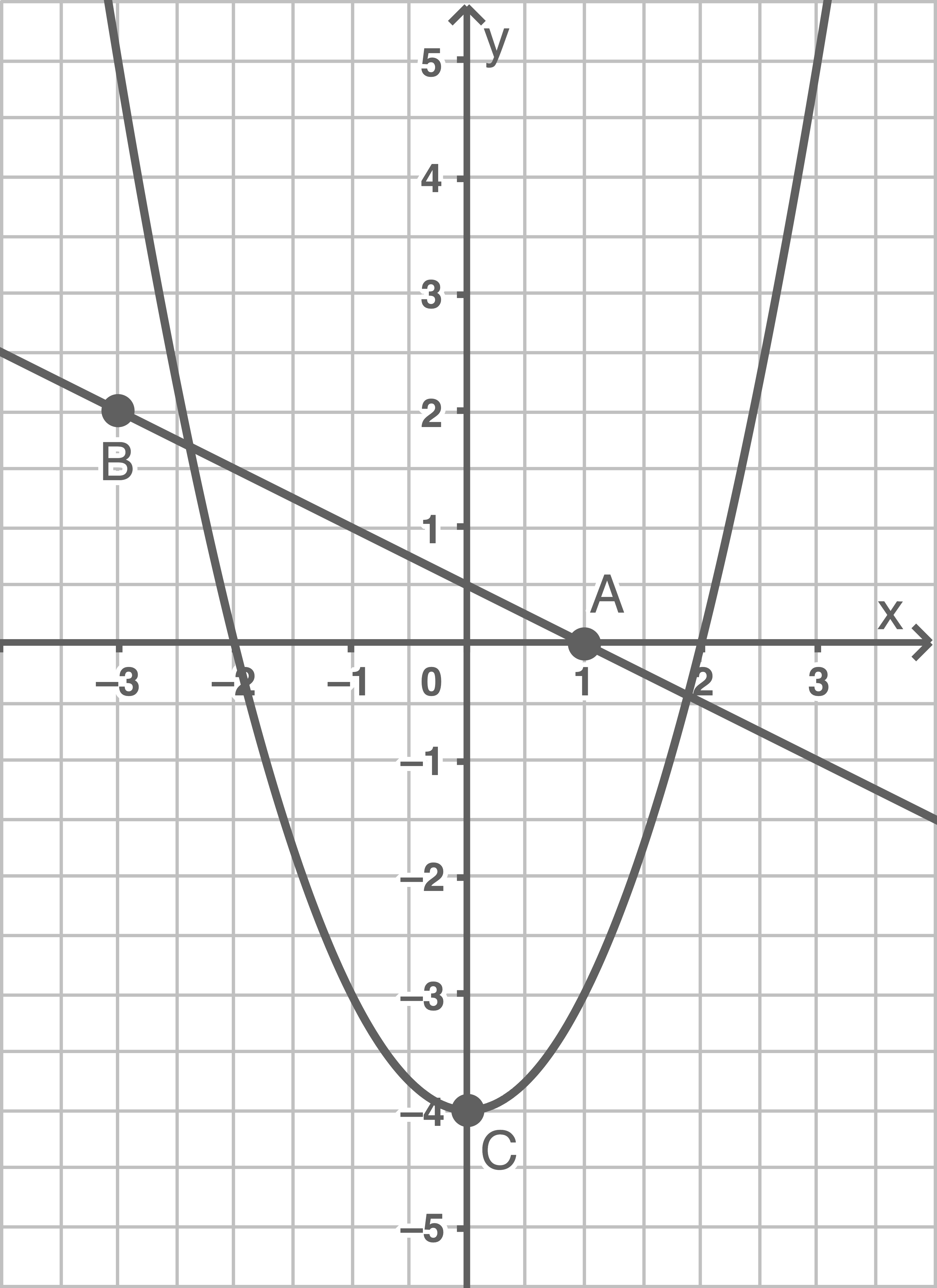

b)
Eine verschobene Normalparabel mit Scheitelpunkt  hat die Funktionsgleichung
hat die Funktionsgleichung  Lösung für Möglichkeit 1
Lösung für Möglichkeit 1
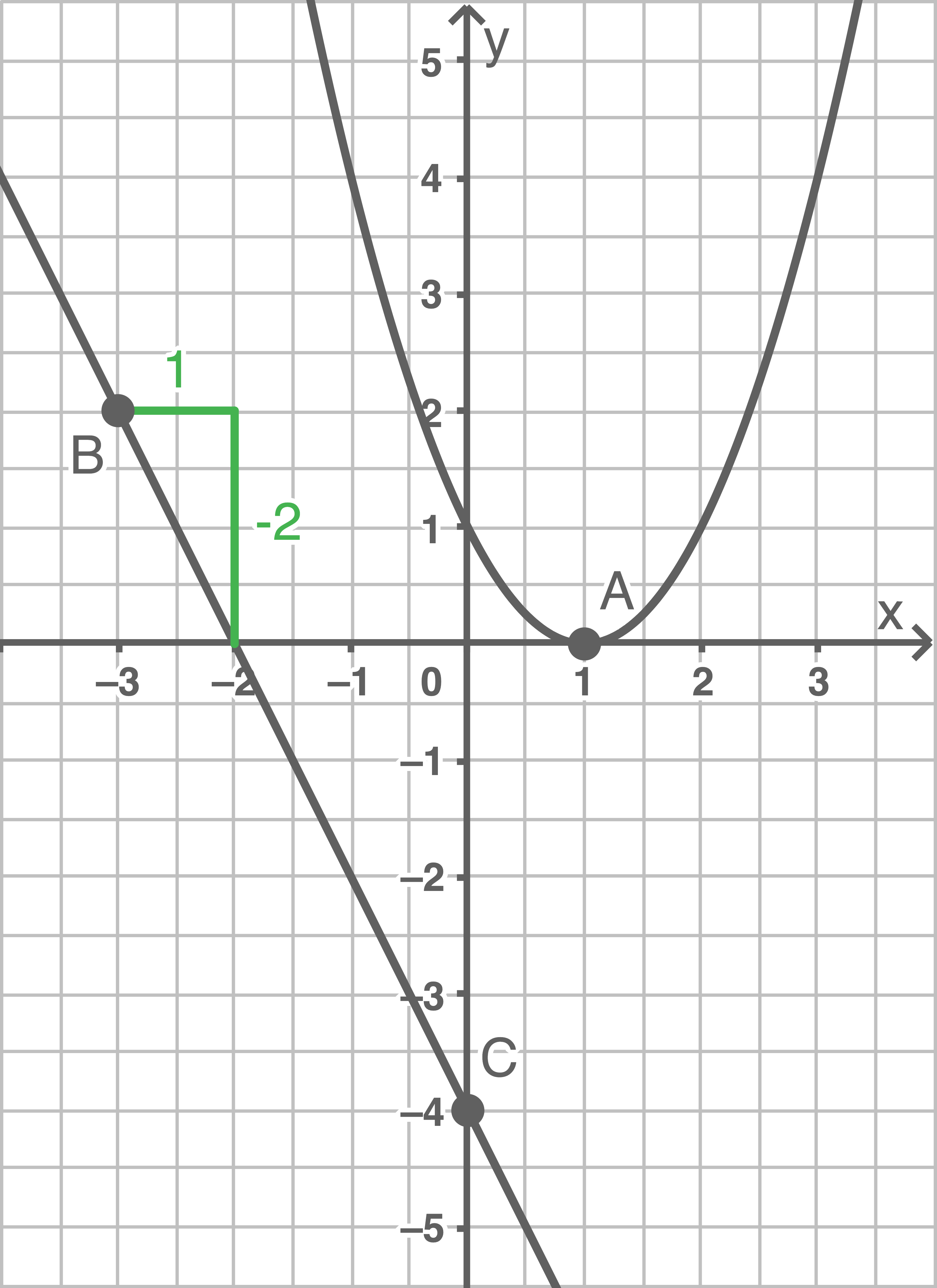
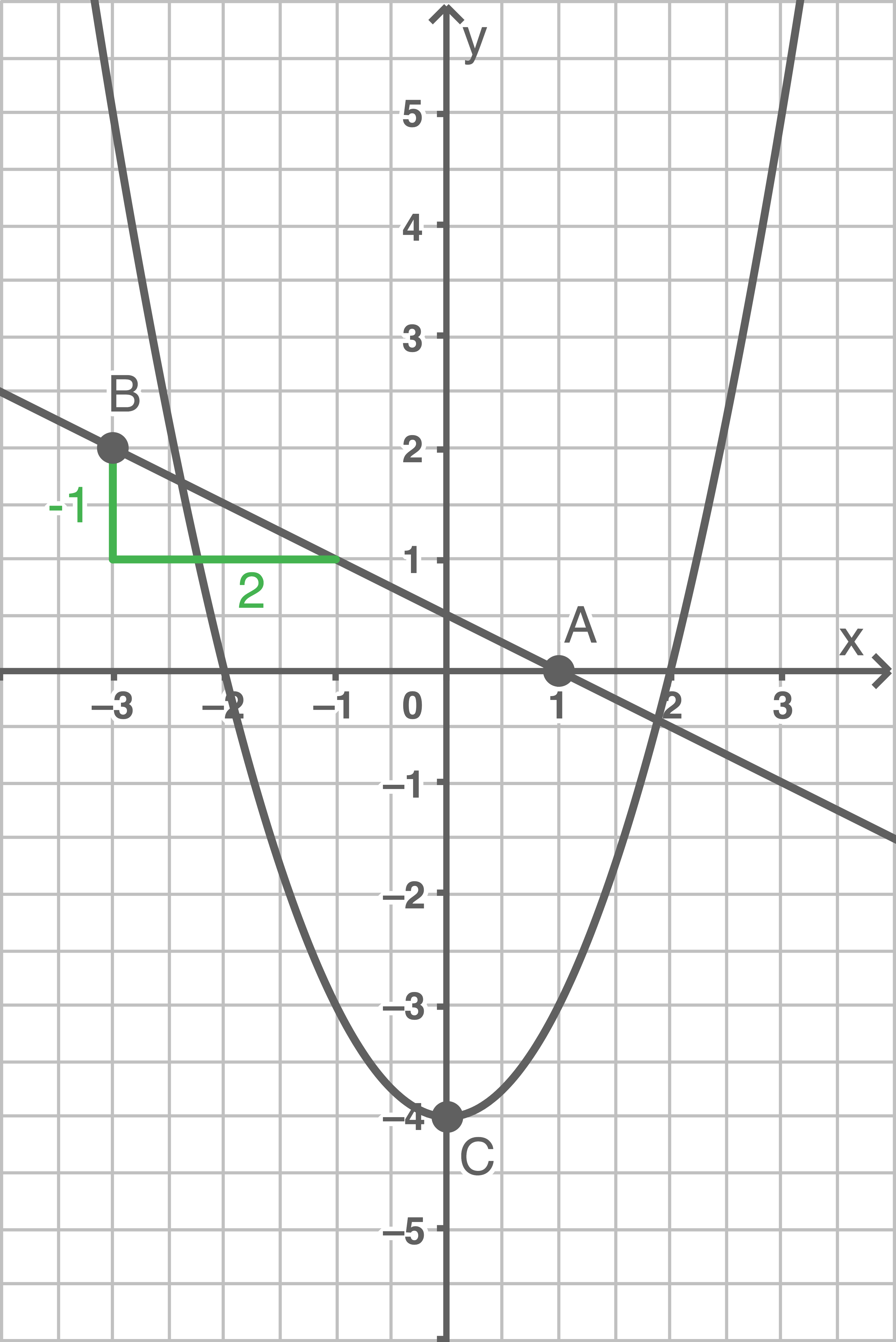

Der Scheitelpunkt der Parabel ist gegeben durch  Damit ist die Funktionsgleichung durch
Damit ist die Funktionsgleichung durch  gegeben.
Die Gerade
gegeben.
Die Gerade  hat die allgemeine Funktionsgleichung
hat die allgemeine Funktionsgleichung  Der
Der  -Achsenabschnitt
-Achsenabschnitt  kann direkt abgelesen werden.
Für die Steigung folgt mit dem Anstiegsdreieck:
kann direkt abgelesen werden.
Für die Steigung folgt mit dem Anstiegsdreieck:  Damit ergibt sich die Geradengleichung
Damit ergibt sich die Geradengleichung 
Lösung für Möglichkeit 2

Der Scheitelpunkt der Parabel ist gegeben durch  Damit ist die Funktionsgleichung durch
Damit ist die Funktionsgleichung durch  gegeben.
Die Gerade
gegeben.
Die Gerade  hat die allgemeine Funktionsgleichung
hat die allgemeine Funktionsgleichung  Der
Der  -Achsenabschnitt
-Achsenabschnitt  kann direkt abgelesen werden.
Für die Steigung folgt mit dem Anstiegsdreieck:
kann direkt abgelesen werden.
Für die Steigung folgt mit dem Anstiegsdreieck:  Damit ergibt sich die Geradengleichung
Damit ergibt sich die Geradengleichung 
9.2
a)
Der Scheitelpunkt des Graphen liegt auf der  -Achse an der Stelle
-Achse an der Stelle 
 Die maximale Höhe der Flugbahn beträgt 30 m.
Die maximale Höhe der Flugbahn beträgt 30 m.
b)
Der gesuchte Abstand ist durch die Entfernung der beiden Nullstellen gegeben.
![\(\begin{array}[t]{rll}
f(x) &=& 0 \\[5pt]
-0,2x^2 +30 &=& 0 \quad \scriptsize \mid\; -30 \\[5pt]
-0,2x^2 &=& -30 \quad \scriptsize \mid\;:(-0,2) \\[5pt]
x^2 &=& 150 \quad \scriptsize \mid\;\sqrt{\,}\\[5pt]
x_{1/2} &=& \pm \sqrt{150} \\[5pt]
x_1 &\approx& 12,25 \\[5pt]
x_2 &\approx& -12,25
\end{array}\)](https://mathjax.schullv.de/655389e21f6d0a57d6ca98981fbfdc082859cdd66067e767785af95389727673?color=5a5a5a) Der Abstand
Der Abstand  der beiden Nullstellen ist gegeben durch:
der beiden Nullstellen ist gegeben durch:
 Die Entfernung zwischen Start- und Landepunkt beträgt ungefähr
Die Entfernung zwischen Start- und Landepunkt beträgt ungefähr 
10.1
a)
Wahrscheinlichkeit für eine richtige Antwort:  Mit den Pfadregeln folgt:
Mit den Pfadregeln folgt:
 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  sind beide Antworten richtig.
sind beide Antworten richtig.
b)
Die Wahrscheinlichkeit, von zwei richtigen Antworten eine richtig anzukreuzen, beträgt  Wurde die erste Antwort richtig angekreutzt, so gibt es noch zwei Antwortmöglichkeiten, von denen eine richtig und eine falsch ist. Die Wahrscheinlichkeit, die richtige Antwort anzukreuzen, beträgt also
Wurde die erste Antwort richtig angekreutzt, so gibt es noch zwei Antwortmöglichkeiten, von denen eine richtig und eine falsch ist. Die Wahrscheinlichkeit, die richtige Antwort anzukreuzen, beträgt also  Mit den Pfadregeln folgt:
Mit den Pfadregeln folgt:
 Die Wahrscheinlichkeit, dass die beiden angekreuzten Antworten richtig sind, beträgt
Die Wahrscheinlichkeit, dass die beiden angekreuzten Antworten richtig sind, beträgt 
10.2
Prozentsatz Gruppe I:
 Prozentsatz Gruppe III:
Prozentsatz Gruppe III:

 der Befragten entsprechen also
der Befragten entsprechen also  Mit dem Dreisatz folgt:
Mit dem Dreisatz folgt:




![\(\begin{array}{rrcll}
& 30\,\% &\mathrel{\widehat{=}}& 66\\[5pt]
& 10\,\% &\mathrel{\widehat{=}}& 22\\[5pt]
& 100\,\% &\mathrel{\widehat{=}}& 220 &
\end{array}\)](https://mathjax.schullv.de/2f2c462988d8fe8bbaf0bdf96b40f950529aea519d09ee540ced08ba95607af2?color=5a5a5a)



 Es wurden 220 Schüler befragt.
Es wurden 220 Schüler befragt.
10.3
Ereignis beschreiben
Ein mögliches Ereignis lautet: „Es werden zwei rote Kugeln gezogen.“
 Alternative Lösungen
Alternative Lösungen
 Baumdiagramm zeichnen
Baumdiagramm zeichnen
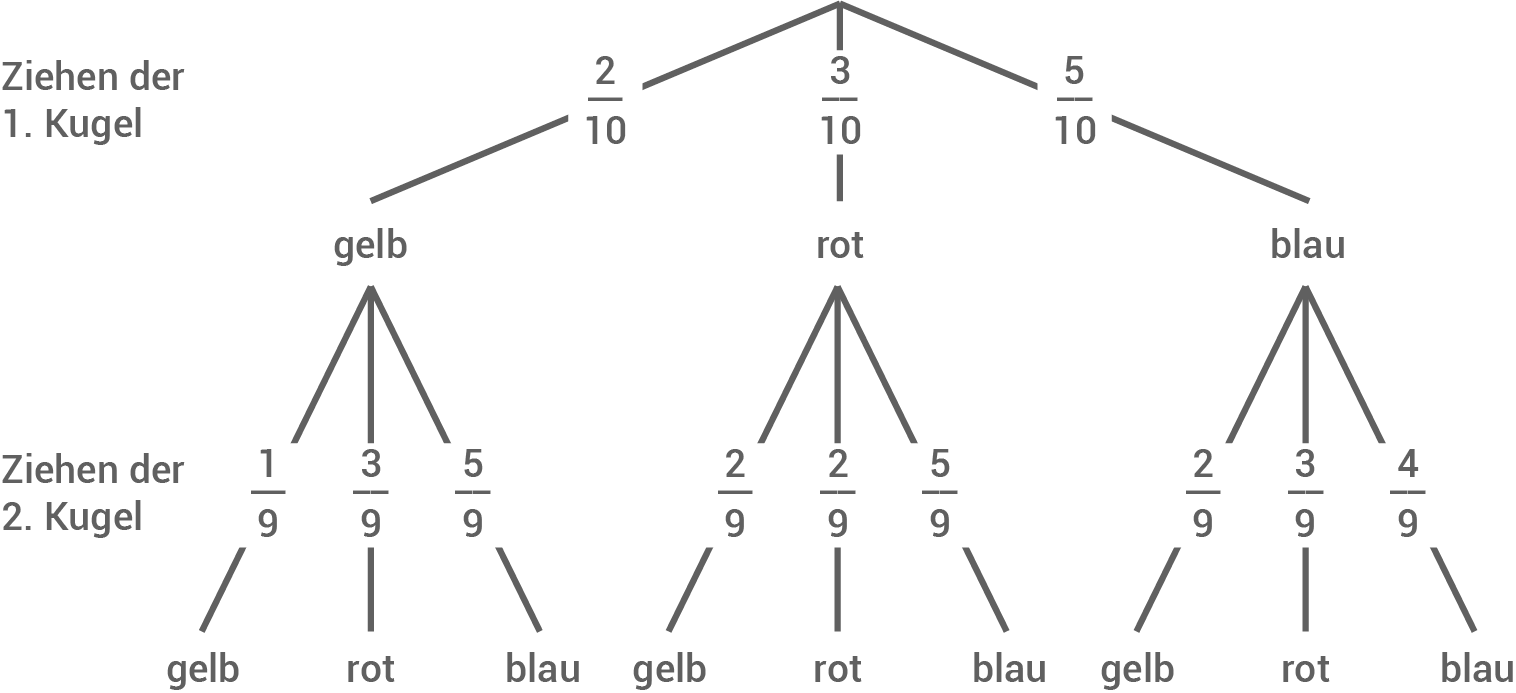

11.1
11.2
11.3
a)
Es muss nur einer der beiden Terme berechnet werden.
![\(\begin{array}[t]{rll}
\text{I}& \dfrac{3a^2 -2a\cdot (a+b)}{3a -(2a+b)} \\[5pt]
=& \dfrac{3\cdot 6^2 -2\cdot 6\cdot (6+(-2))}{3\cdot 6 -(2\cdot 6+(-2))} \\[5pt]
=& \dfrac{60}{8} \\[5pt]
=& \dfrac{15}{2}
\end{array}\)](https://mathjax.schullv.de/4b30262f712d7856d02650659db6f03575919126551093b6b805c75d5df49762?color=5a5a5a)
![\(\begin{array}[t]{rll}
\text{II}&\dfrac{a^2 -2ab}{a-b} \\[5pt]
=& \dfrac{6^2-2\cdot 6\cdot (-2)}{6-(-2)} \\[5pt]
=& \dfrac{60}{8} \\[5pt]
=& \dfrac{15}{2}
\end{array}\)](https://mathjax.schullv.de/ace8db0ad6dab9431f94eb7aa8bd2ba95425023777aca8204204eef748a26a7e?color=5a5a5a)
b)
12.1
a)
b)
c)
Zwei der drei Eckpunkte des Dreiecks sind Endpunkte eines Durchmessers des Kreises. Der dritte Eckpunkt  liegt auf dem Kreis. Mit dem Satz des Thales folgt daher, dass das Dreieck im Punkt
liegt auf dem Kreis. Mit dem Satz des Thales folgt daher, dass das Dreieck im Punkt  einen rechten Winkel besitzt.
einen rechten Winkel besitzt.
12.2
Höhenunterschied zwischen den beiden Stationen:
 Waagrechte Entfernung:
Waagrechte Entfernung:
![\(\begin{array}[t]{rll}
\ell&=& 50\,000\cdot 8\,\text{cm}\\[5pt]
&=& 400\,000\,\text{cm}\\[5pt]
&=& 4\,000\,\text{m}
\end{array}\)](https://mathjax.schullv.de/70fd71ad968a62fff9abece7bf49ed8b78bd238c6b2b32926aa8e223da2e4b16?color=5a5a5a) Skizze des Sachverhalts:
Skizze des Sachverhalts:
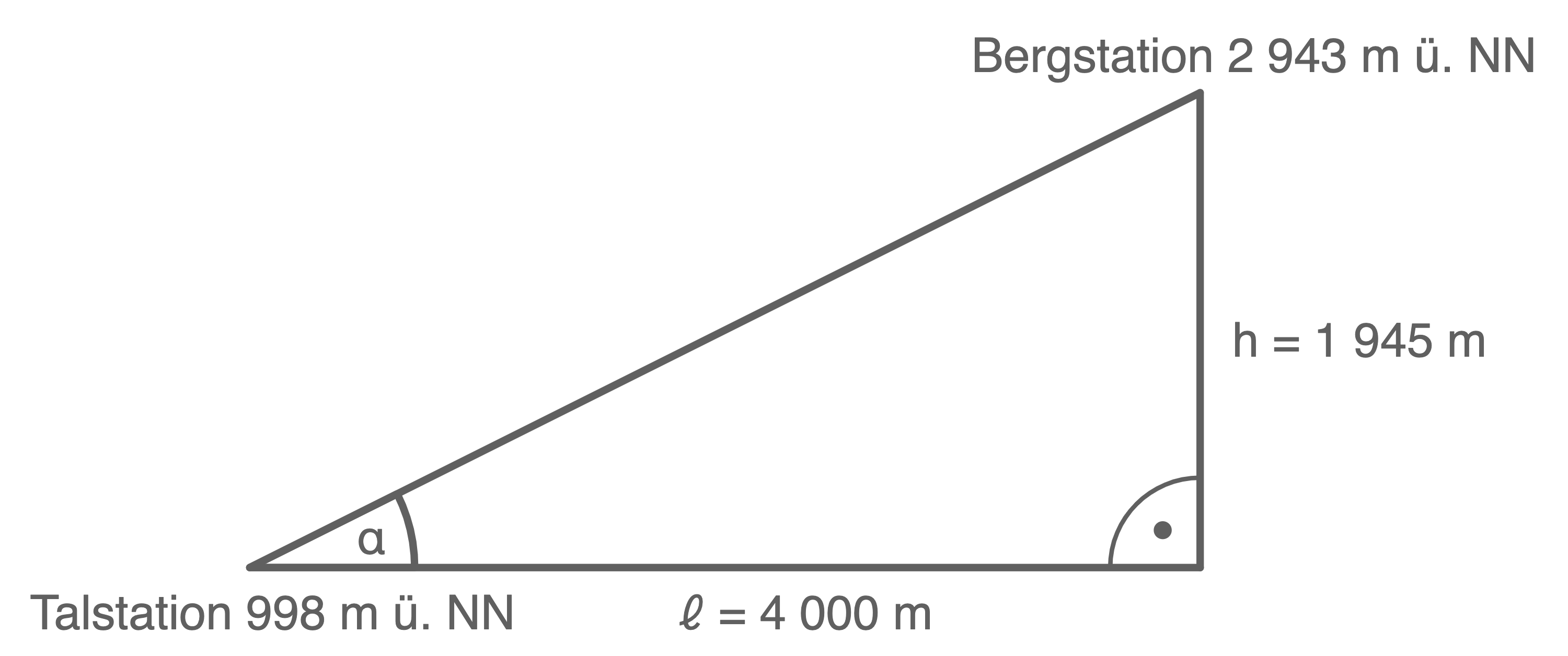 Mit dem Tangens folgt nun:
Mit dem Tangens folgt nun:
![\(\begin{array}[t]{rll}
\tan \alpha &=& \dfrac{h}{\ell}\\[5pt]
\tan \alpha &=& \dfrac{1\,945\,\text{m}}{4\,000\,\text{m}} \\[5pt]
\tan \alpha &=& 0,48625 \quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\alpha &\approx& 25,9^{\circ} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/78813cbda59b99349361e8d5a0213b6814aa4c3fd3883d573886bc4615c07e3c?color=5a5a5a) Der durchschnittliche Anstiegswinkel der Zugspitzbahn beträgt ca.
Der durchschnittliche Anstiegswinkel der Zugspitzbahn beträgt ca. 
