Pflichtaufgaben
1
In Thüringen wurden 2015 insgesamt 396 Tonnen Strauchbeeren auf 162 Hektar Anbaufläche geerntet.
 der Erntemenge.
der Erntemenge.
 vergrößert.
vergrößert.

a)
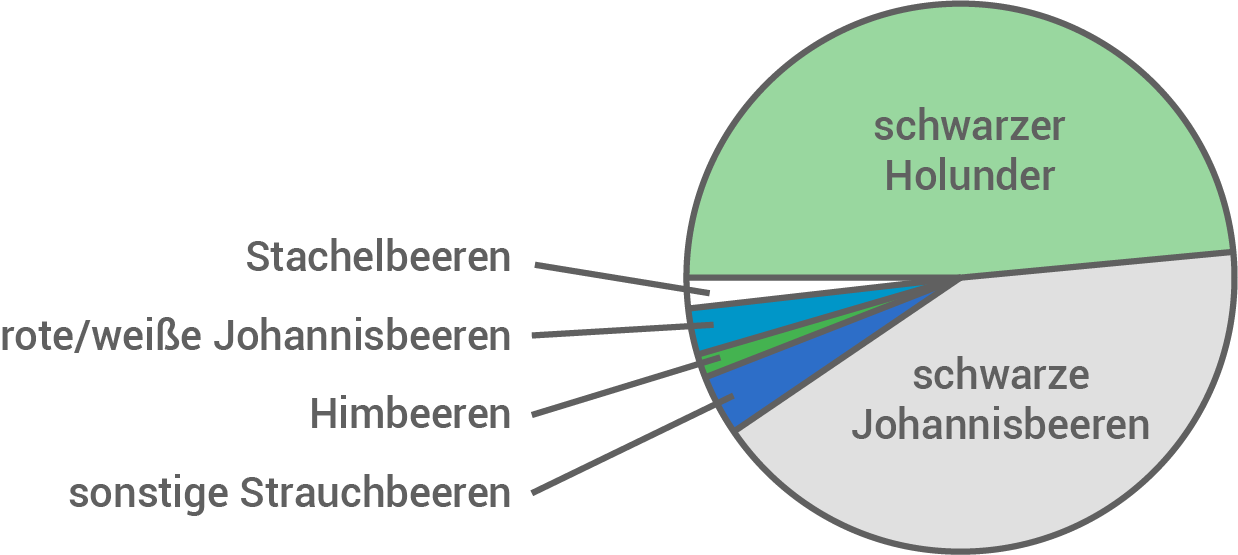
Ermittle den prozentualen Anteil der schwarzen Johannisbeeren an der Gesamtmenge der Strauchbeeren.
Messe dafür den entsprechenden Winkel im Kreisdiagramm.
Auf schwarzen Holunder entfielen Messe dafür den entsprechenden Winkel im Kreisdiagramm.
1 BE
b)
Wie viele Tonnen schwarzer Holunder wurden geerntet?
Die gesamte Anbaufläche wurde 2015 gegenüber 2014 um
1 BE
c)
Berechne die Größe der Anbaufläche für das Jahr 2014.
1 BE
2
Für einen Kegel soll gelten, dass Radius und Körperhöhe gleich groß sind.
a)
Stelle einen solchen Kegel im Zweitafelbild dar.
2 BE
b)
Begründe, dass zur Berechnung des Volumens dieses Kegels auch gilt:

1 BE
3
Zwei Mitspieler erhalten jeweils 20 Karten, auf denen die Zahlen 1 bis 20 stehen. Jeder Mitspieler legt seine gemischten Karten vor sich verdeckt auf einen Stapel.
Aufgedeckte Karten werden nicht zurückgelegt. Der Spieler deckt eine Karte mit der Zahl 7 auf.
deckt eine Karte mit der Zahl 7 auf.
 die Zahl 5 auf. Spieler
die Zahl 5 auf. Spieler  gewinnt, wenn er nun eine größere Zahl als 5 aufdeckt.
gewinnt, wenn er nun eine größere Zahl als 5 aufdeckt.
Aufgedeckte Karten werden nicht zurückgelegt. Der Spieler
a)
Gib die Wahrscheinlichkeit dafür an, dass der Spieler  eine Karte mit einer größeren Zahl vom Stapel aufdeckt.
eine Karte mit einer größeren Zahl vom Stapel aufdeckt.
Beide Spieler decken zuerst die Zahl 7 auf. Dann deckt Spieler
1 BE
b)
Gib die Wahrscheinlichkeit dafür an, dass Spieler  gewinnt.
gewinnt.
1 BE
4
Jonas misst sein neues Zimmer aus.
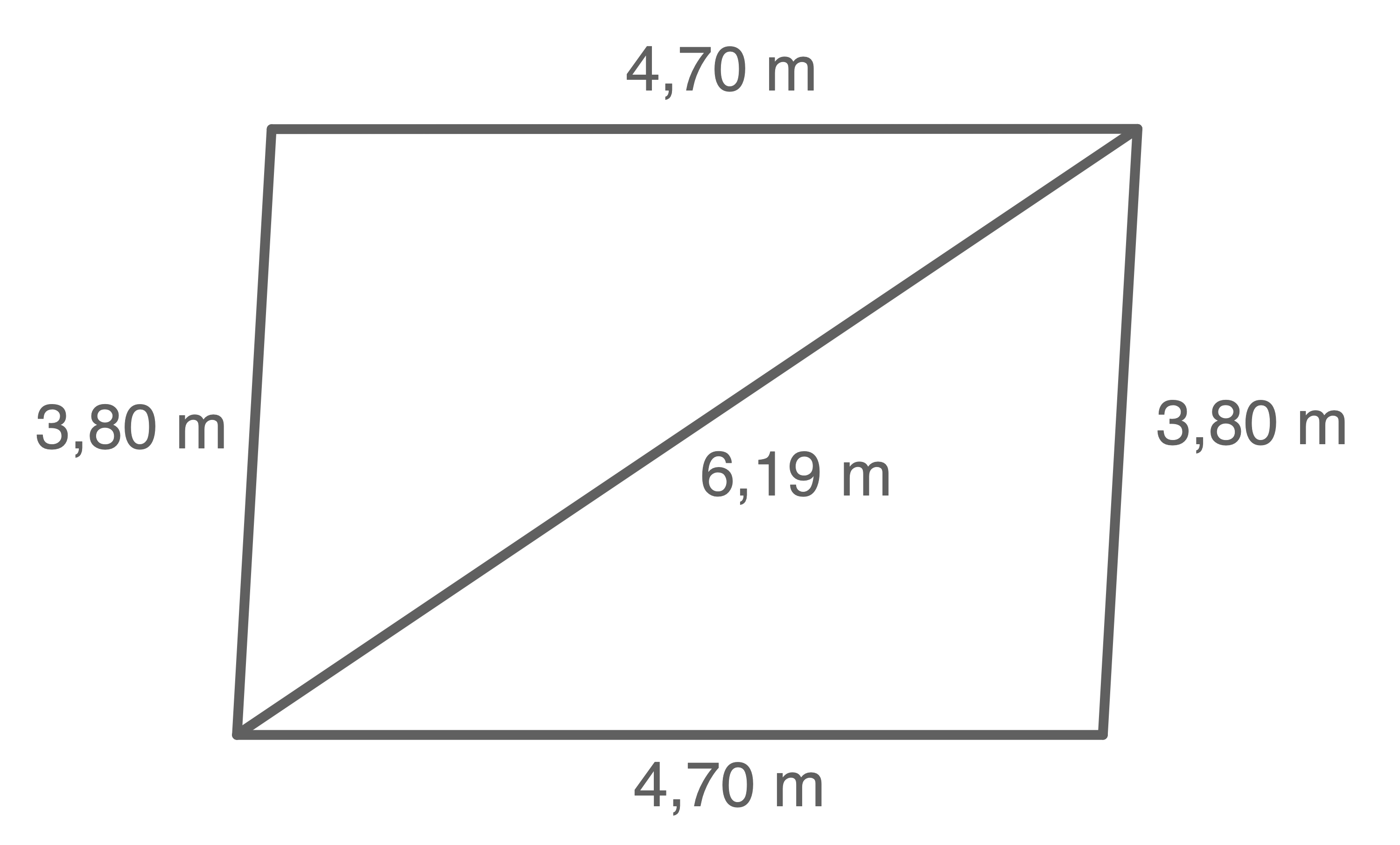 Weise rechnerisch nach, dass das Zimmer nicht rechtwinklig ist.
Weise rechnerisch nach, dass das Zimmer nicht rechtwinklig ist.

Skizze nicht maßstäblich
1 BE
5
Von einem Viereck  sind folgende Stücke bekannt:
sind folgende Stücke bekannt:
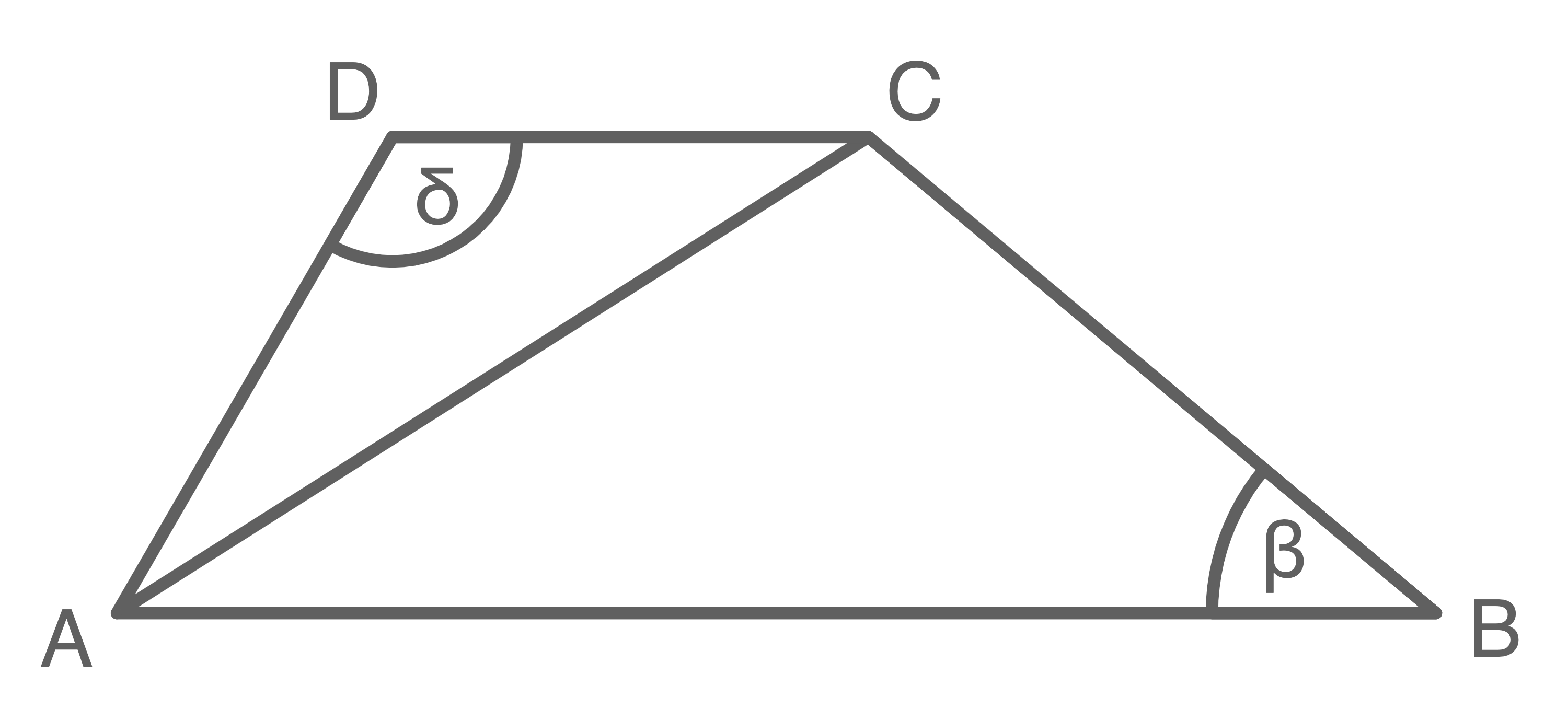 Berechne den Flächeninhalt des Dreiecks
Berechne den Flächeninhalt des Dreiecks 

Skizze nicht maßstäblich
3 BE
6
Gegeben ist eine Wertetabelle für die Potenzfunktion  mit
mit  und
und 
Eine weitere Funktion hat die Gleichung  mit
mit 
a)
Stelle die Funktionen  und
und  in einem Koordinatensystem graphisch dar.
in einem Koordinatensystem graphisch dar.
2 BE
b)
Gib die Gleichung der Funktion  an.
an.
1 BE
c)
Berechne die Nullstellen der Funktion 
1 BE
d)
Weise rechnerisch nach, dass der Graph der Funktion  auch durch den Punkt
auch durch den Punkt  verläuft.
verläuft.
1 BE
7
Frau Pohl möchte eine Töpferwerkstatt eröffnen und Krüge herstellen.
Sie plant die zu erwartenden Kosten: Festkosten pro Monat:
Materialkosten pro Krug: In einem Monat möchte Frau Pohl durch Herstellung und Verkauf von 350 Krügen einen Gewinn von
In einem Monat möchte Frau Pohl durch Herstellung und Verkauf von 350 Krügen einen Gewinn von  erwirtschaften.
Ermittle den dafür notwendigen Verkaufspreis für einen Krug.
erwirtschaften.
Ermittle den dafür notwendigen Verkaufspreis für einen Krug.
Sie plant die zu erwartenden Kosten: Festkosten pro Monat:
Materialkosten pro Krug:
2 BE
8
In einer Zeitung stand: „ Bällchen müssen aus dem See gefischt werden.“
Bällchen müssen aus dem See gefischt werden.“
Diese Bällchen dienen der Franken-Therme im Winter als Wärmeisolation des beheizten Sees. Damit werden etwa der Fläche des Sees abgedeckt. Jedes Bällchen hat einen Durchmesser von
der Fläche des Sees abgedeckt. Jedes Bällchen hat einen Durchmesser von 
Auf dem See schwimmen blaue und
blaue und  grüne Bällchen.
grüne Bällchen.
Diese Bällchen dienen der Franken-Therme im Winter als Wärmeisolation des beheizten Sees. Damit werden etwa
Auf dem See schwimmen
a)
Berechne den Flächeninhalt der Wasseroberfläche des Sees. Gib diesen in Quadratmeter an.
Zum Einsammeln der Bällchen im Frühjahr holen sich die Mitarbeiter der Franken-Therme Hilfe. Es werden zehn Teams mit jeweils vier Personen gebildet, die innerhalb von 15 Minuten alle Bällchen einsammeln.
3 BE
b)
Wie viel Zeit würden nur zwei Mitarbeiter für diese Tätigkeit benötigen?
1 BE
c)
Gib die Wahrscheinlichkeit dafür an, dass das erste zufällig herausgefischte Bällchen grün ist.
1 BE
1
a)
Eine Winkelmessung mit dem Geodreieck oder Winkelmesser liefert für die schwarzen Johannisbeeren einen Innenwinkel von  Lösung mit der Lösungsformel
Lösung mit der Lösungsformel


![\(\begin{array}[t]{rll}
p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt]
p\,\%&=& \dfrac{150°}{360°}\cdot 100\,\% \\[5pt]
p\,\%&\approx& 42\,\%
\end{array}\)](https://mathjax.schullv.de/bcd3df6a29cf82915a10cf52e65fc900a785793a07b6f79767361b48b0f0ee27?color=5a5a5a) Lösung mit Dreisatz
Lösung mit Dreisatz




![\(\begin{array}{rcl}
360° & \mathrel{\widehat{=}}& 100\,\%\\[5pt]
1° & \mathrel{\widehat{=}}& \dfrac{100}{360}\,\%\\[5pt]
150° & \mathrel{\widehat{\approx}}& 42\,\%
\end{array}\)](https://mathjax.schullv.de/8bc45ece54ced427e36e48054e7bd597562a1244af502f227e727fd5da927887?color=5a5a5a)



 Die schwarzen Johannisbeeren nehmen
Die schwarzen Johannisbeeren nehmen  der Gesamtmenge der Strauchbeeren ein.
der Gesamtmenge der Strauchbeeren ein.
b)
Lösung mit der Lösungsformel


![\(\begin{array}[t]{rll}
W&=& \dfrac{G\cdot p\,\%}{100\,\%} \\[5pt]
W&=& \dfrac{396\,\text{t}\cdot 48,5\,\%}{100\,\%} \\[5pt]
W&\approx& 192 \,\text{t}
\end{array}\)](https://mathjax.schullv.de/6e8ce227e03a8b095a462b9634581924f3c4c5bacf854cd6af6ba9be242ede43?color=5a5a5a) Lösung mit Dreisatz
Lösung mit Dreisatz




![\(\begin{array}{rrcll}
&100\,\%&\mathrel{\widehat{=}}&396\,\text{t}\\[5pt]
&1\,\%&\mathrel{\widehat{=}}&3,96\,\text{t}\\[5pt]
&48,5\,\%&\mathrel{\widehat{\approx}}&192\,\text{t}&
\end{array}\)](https://mathjax.schullv.de/1dd9c14f806014baeb357327bc7096d6a07dde7077863e6bf4b8bf0119891f5d?color=5a5a5a)



 Es wurden ca. 192 Tonnen schwarzer Holunder geerntet.
Es wurden ca. 192 Tonnen schwarzer Holunder geerntet.
c)
Lösung mit Lösungsformel


![\(\begin{array}[t]{rll}
G&=& \dfrac{W\cdot 100\,\%}{p\,\%} \\[5pt]
G&=& \dfrac{162\,\text{ha}\cdot 100\,\%}{113\,\%} \\[5pt]
G&\approx& 143 \,\text{ha}
\end{array}\)](https://mathjax.schullv.de/b952d6055347bf1048afb5a97b0fe4300bc0dd9e6e7b772968b8a294ef447e19?color=5a5a5a) Lösung mit Dreisatz
Lösung mit Dreisatz




![\(\begin{array}{rrcll}
&113\,\%&\mathrel{\widehat{=}}&162\,\text{ha}\\[5pt]
&1\,\%&\mathrel{\widehat{=}}&\dfrac{162}{113}\,\text{ha}\\[5pt]
&100\,\%&\mathrel{\widehat{\approx}}& 143\,\text{ha}&
\end{array}\)](https://mathjax.schullv.de/afdfa675277c27a39cd9f704bded9186d224c27cd28462ff3a2c228673b1275b?color=5a5a5a)



 2014 war die Anbaufläche ca.
2014 war die Anbaufläche ca.  Hektar groß.
Hektar groß.
2
a)
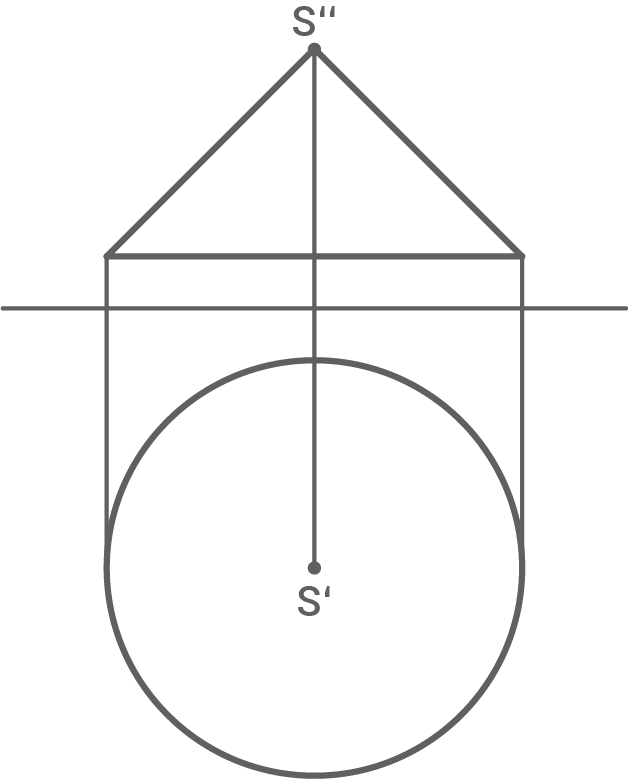
b)
Für den Kegel gilt  Mit der Formel für das Volumen eines Kegels gilt:
Mit der Formel für das Volumen eines Kegels gilt:
![\(\begin{array}[t]{rll}
V&=& \dfrac{1}{3}\cdot \pi\cdot r^2\cdot h \quad \scriptsize \mid\; h=r \\[5pt]
&=& \dfrac{1}{3}\cdot \pi\cdot r^2\cdot r \\[5pt]
&=& \dfrac{1}{3}\cdot \pi\cdot r^3
\end{array}\)](https://mathjax.schullv.de/b15ecedef6cfa291e63da49359c57bbeff756133a31f65a2f74a87416ae6c1d7?color=5a5a5a)
3
a)
Anzahl möglicher Ergebnisse: 
Anzahl günstiger Ergebnisse:
![\(\begin{array}[t]{rll}
& P(\text{Zahl größer 7}) \\[5pt]
=& \dfrac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl möglicher Ergebnisse}} \\[5pt]
=& \dfrac{13}{20} \\[5pt]
=& 65\,\%
\end{array}\)](https://mathjax.schullv.de/8e62540d636089273b3938b4d5dfbbfd425a60e5f079d544031e4d9f304c1c8a?color=5a5a5a) Die Wahrscheinlichkeit beträgt
Die Wahrscheinlichkeit beträgt 
Anzahl günstiger Ergebnisse:
b)
Anzahl möglicher Ergebnisse (7 wurde bereits aufgedeckt): 
Anzahl günstiger Ergebnisse (Zahlen größer 5 außer 7):
![\(\begin{array}[t]{rll}
& P(\text{Zahl größer 5}) \\[5pt]
=& \dfrac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl möglicher Ergebnisse}} \\[5pt]
=& \dfrac{14}{19} \\[5pt]
\approx& 74\,\%
\end{array}\)](https://mathjax.schullv.de/8f5be0c27fcb3e2c162caf60af17fe4ac20a22083a26e97e7dac5da70916eb53?color=5a5a5a) Die Wahrscheinlichkeit beträgt ungefähr
Die Wahrscheinlichkeit beträgt ungefähr 
Anzahl günstiger Ergebnisse (Zahlen größer 5 außer 7):
4
Die eingezeichnete Diagonale teilt den viereckigen Grundriss in zwei kongruente Dreiecke. Wenn diese rechtwinklig sind, müssen die zugehörigen Maße den Satz des Pythagoras erfüllen. Es muss also gelten:
![\(\begin{array}[t]{rll}
(3,80\,\text{m})^2+(4,70\,\text{m})^2&=& (6,19\,\text{m})^2 \\[5pt]
36,5\,\text{m}^2&=& 38,3\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/59e49fa313a59c81f3a5f4ca59220d8252cc92101bef22ef934e3f389d24facc?color=5a5a5a) Die Aussage ist falsch, daher ist der Satz des Pythagoras nicht erfüllt. Die Dreiecke und damit auch das Zimmer sind also nicht rechtwinklig.
Die Aussage ist falsch, daher ist der Satz des Pythagoras nicht erfüllt. Die Dreiecke und damit auch das Zimmer sind also nicht rechtwinklig.
5
Länge der Strecke  berechnen
Mithilfe des Kosinussatzes im Dreieck
berechnen
Mithilfe des Kosinussatzes im Dreieck  ergibt sich:
Winkelgröße berechnen
Mithilfe des Sinussatzes kann die Größe des Winkels
ergibt sich:
Winkelgröße berechnen
Mithilfe des Sinussatzes kann die Größe des Winkels  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\dfrac{\overline{BC}}{\sin\sphericalangle CAB}&=& \dfrac{\overline{AC}}{\sin\beta} \quad \scriptsize \mid\; \cdot \sin\sphericalangle CAB \\[5pt]
\overline{BC}&=& \dfrac{\overline{AC}}{\sin\beta}\cdot \sin\sphericalangle CAB \quad \scriptsize \mid\; : \overline{AC} \\[5pt]
\dfrac{\overline{BC}}{\overline{AC}}&=& \dfrac{\sin\sphericalangle CAB}{\sin\beta} \\[5pt]
\dfrac{5,0\,\text{cm}}{6,8\,\text{cm}}&=& \dfrac{\sin\sphericalangle CAB}{\sin 40^{\circ}} \quad \scriptsize \mid\; \cdot\sin 40^{\circ} \\[5pt]
\dfrac{5,0\,\text{cm}}{6,8\,\text{cm}}\cdot \sin 40^{\circ}&=& \sin\sphericalangle CAB \\[5pt]
0,47264 &\approx& \sin\sphericalangle CAB \quad \scriptsize \mid\;\sin^{-1} \\[5pt]
28^{\circ}&\approx& \sphericalangle CAB \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6ffe273897adff4f7d825bb567fa81ced596771342c5ce8f5f0a24e44800ef4a?color=5a5a5a) Mithilfe der Winkelsumme ergibt sich die Größe des Winkels
Mithilfe der Winkelsumme ergibt sich die Größe des Winkels 
![\(\begin{array}[t]{rll}
\sphericalangle BCA &=& 180^{\circ} - 40^{\circ} - 28^{\circ} \\[5pt]
&=& 112^{\circ}
\end{array}\)](https://mathjax.schullv.de/d427d99b003640778c927f13412879a0e3c7ba635a250691823c319dbeca72a8?color=5a5a5a) Flächeninhalt berechnen
Mithilfe des Sinus kann nun der Flächeninhalt des Dreiecks
Flächeninhalt berechnen
Mithilfe des Sinus kann nun der Flächeninhalt des Dreiecks  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
A&=& \dfrac{1}{2}\cdot \overline{BC} \cdot \overline{AC}\cdot \sin \sphericalangle BCA\\[5pt]
&=& \dfrac{1}{2}\cdot 5,0\,\text{cm} \cdot 6,8\,\text{cm} \cdot \sin 112^{\circ} \\[5pt]
&\approx& 16\,\text{cm}^2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/585a8fbe61dc0685b93e921862b7557b6fea2e9dcd7b91973b6d12c4c1e5e3d9?color=5a5a5a) Der Flächeninhalt des Dreiecks
Der Flächeninhalt des Dreiecks  beträgt ungefähr
beträgt ungefähr 
6
a)
Eine Wertetabelle für  ist bereits angegeben. Bei der Funktion
ist bereits angegeben. Bei der Funktion  handelt es sich um eine verschobene Normalparabel. Um diese grafisch darstellen zu können, wird der Scheitelpunkt berechnet:
handelt es sich um eine verschobene Normalparabel. Um diese grafisch darstellen zu können, wird der Scheitelpunkt berechnet:
 Es gilt
Es gilt  und
und 


 Damit können die beiden Funktionen in ein Koordinatensystem dargestellt werden.
Damit können die beiden Funktionen in ein Koordinatensystem dargestellt werden.
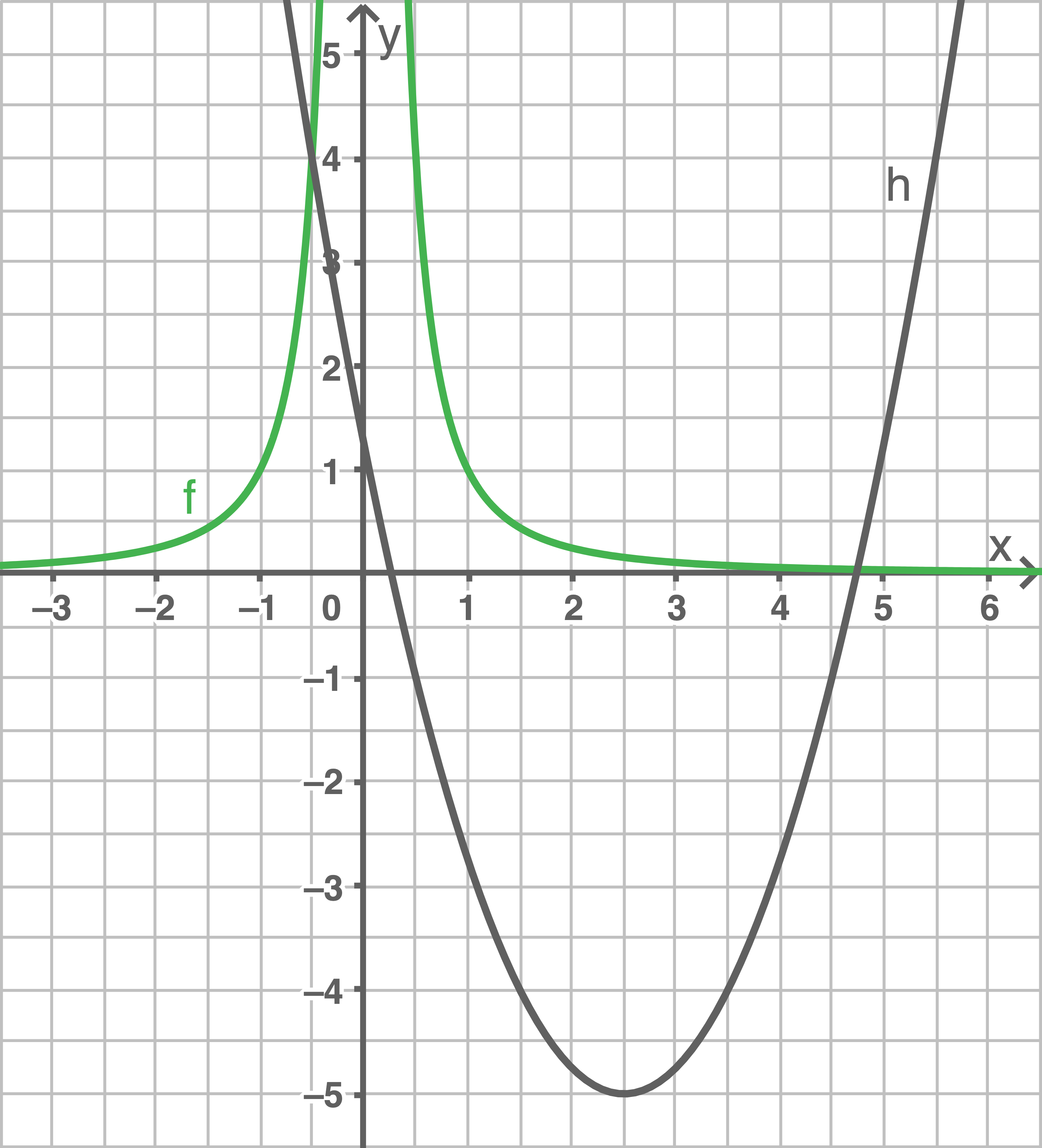

b)
Der Graph der Funktion  ist eine Hyperbel, die nur positive Wert annimmt. Der Exponent muss also gerade sein.
Vermutete Gleichung:
ist eine Hyperbel, die nur positive Wert annimmt. Der Exponent muss also gerade sein.
Vermutete Gleichung:  Einsetzen von Werten zur Überprüfung:
Einsetzen von Werten zur Überprüfung:

 Die Ergebnisse stimmen mit den Werten aus der Wertetabelle überein. Die Gleichung der Funktion lautet also
Die Ergebnisse stimmen mit den Werten aus der Wertetabelle überein. Die Gleichung der Funktion lautet also 
c)
Die Nullstellen können mit der Lösungsformel berechnet werden.
![\(\begin{array}[t]{rll}
h(x)&=& x^2-5x+1,25 \\[5pt]
0&=& x^2-5x+1,25 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/9cee146cb0aeace3f87328db31a5407135b9f6272efd88d1292cd5f3cf12a005?color=5a5a5a) Es gilt
Es gilt  und
und 
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{-5}{2}\pm \sqrt{\left(\dfrac{-5}{2} \right)^2 -1,25} \\[5pt]
&=& 2,5\pm \sqrt{5} \\[5pt]
x_1&=& 2,5 - \sqrt{5} \\[5pt]
x_2&=& 2,5 + \sqrt{5}
\end{array}\)](https://mathjax.schullv.de/52a77aa0523c76984c8dd5d246ed044c05e767dfdbe1b7c271b1824341581f85?color=5a5a5a) Die Nullstellen von
Die Nullstellen von  sind
sind  und
und 
d)
Der Graph von  verläuft durch den Punkt
verläuft durch den Punkt  wenn
wenn  gilt.
gilt.
![\(\begin{array}[t]{rll}
h(-0,5)&=& (-0,5)^2 -5\cdot (-0,5)+1,25 \\[5pt]
&=& 4
\end{array}\)](https://mathjax.schullv.de/487698936235e5ff6aded5ffb98ce38a90c1b7e8e481ad199ade4ab1fa59c25a?color=5a5a5a) Der Graph der Funktion
Der Graph der Funktion  verläuft also durch den Punkt
verläuft also durch den Punkt 
7
Monatliche Kosten für 350 Krüge:
 Notwendige Einnahmen, um
Notwendige Einnahmen, um  Gewinnn zu erwirtschaften:
Gewinnn zu erwirtschaften:
 Frau Pohl muss also die
Frau Pohl muss also die  Krüge so verkaufen, dass sie damit
Krüge so verkaufen, dass sie damit  einnimmt.
einnimmt.
 Ein Krug muss für
Ein Krug muss für  verkauft werden.
verkauft werden.
8
a)
Die  Bällchen decken gemeinsam
Bällchen decken gemeinsam  des Sees ab. Jedes Bällchen deckt einen kreisförmigen Teil des Sees ab, der einen Durchmesser von
des Sees ab. Jedes Bällchen deckt einen kreisförmigen Teil des Sees ab, der einen Durchmesser von  also einen Radius von
also einen Radius von  hat.
Mithilfe der Formel für den Flächeninhalt eines Kreises lässt sich die Fläche berechnen, die von einem Bällchen abgedeckt wird:
hat.
Mithilfe der Formel für den Flächeninhalt eines Kreises lässt sich die Fläche berechnen, die von einem Bällchen abgedeckt wird:
![\(\begin{array}[t]{rll}
A_{B_1}&=& \pi \cdot r^2 \\[5pt]
&=& \pi \cdot (3\,\text{cm})^2 \\[5pt]
&\approx& 28\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/5096fbe9a8ce26c6fa9e74590ec1f6ebf924925675595f568b9f163f457a3e95?color=5a5a5a) Insgesamt befinden sich
Insgesamt befinden sich  Bällchen auf dem See. Die Fläche, die von allen Bällchen abgedeckt wird, ist daher gegeben durch:
Bällchen auf dem See. Die Fläche, die von allen Bällchen abgedeckt wird, ist daher gegeben durch:
![\(\begin{array}[t]{rll}
A_B&=& 160\,000 \cdot A_{B_1} \\[5pt]
&\approx& 160\,000 \cdot 28\,\text{cm}^2 \\[5pt]
&=& 4\,480\,000\,\text{cm}^2\\[5pt]
&=& 448\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/03ddf7d0722ab4ec23fb85fcaa44e03a5229445825d158862f42b65682b288ad?color=5a5a5a) Fläche des Sees mit der Lösungsformel berechnen
Fläche des Sees mit der Lösungsformel berechnen


![\(\begin{array}[t]{rll}
G&=& \dfrac{W\cdot 100\,\%}{p\,\%} \\[5pt]
G&\approx& \dfrac{448\,\text{m}^2\cdot 100\,\%}{90\,\%} \\[5pt]
G&\approx& 498\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/b8a9eda23a800e21c95cfeaab0e0117331d3379cb8dd67013932cd28989d25b8?color=5a5a5a) Fläche des Sees mit dem Dreisatz berechnen
Die Fläche, die von den Bällchen bedeckt ist, entspricht
Fläche des Sees mit dem Dreisatz berechnen
Die Fläche, die von den Bällchen bedeckt ist, entspricht  der Seeoberfläche.
der Seeoberfläche.




![\(\begin{array}{rrcll}
&90\,\%&\mathrel{\widehat{=}}& 448\,\text{m}^2\\[5pt]
&1\,\%&\mathrel{\widehat{=}}&\dfrac{448}{90}\,\text{m}^2\\[5pt]
&100\,\%&\mathrel{\widehat{\approx}}& 498\,\text{m}^2&
\end{array}\)](https://mathjax.schullv.de/0e79c2650901ba6a6770c9843086490ce5604a9ab486f06b9c3f41ff6b3062ce?color=5a5a5a)



 Die Oberfläche des Sees ist ungefähr
Die Oberfläche des Sees ist ungefähr  groß.
groß.
b)
Lösung mit Dreisatz




![\(\begin{array}{rrcll}
&40\,\text{Personen}&\mathrel{\widehat{=}}& 15\,\text{min}\\[5pt]
&1\,\text{Person}&\mathrel{\widehat{=}}&\dfrac{15}{40}\,\text{min}\\[5pt]
&2\,\text{Personen}&\mathrel{\widehat{=}}&300\,\text{min}
\end{array}\)](https://mathjax.schullv.de/ab368a3531c9eb1d99db858adb50e1763cdbc5d31930156bea3cf387ef806985?color=5a5a5a)



 Lösung mit Gleichung
Die Zeit
Lösung mit Gleichung
Die Zeit  die nur zwei Mitarbeiter benötigen würden, lässt sich durch Lösen der folgenden Gleichung ermitteln.
die nur zwei Mitarbeiter benötigen würden, lässt sich durch Lösen der folgenden Gleichung ermitteln.
![\(\begin{array}[t]{rll}
40\cdot 15\,\text{min}&=& 2\cdot x \quad \scriptsize \mid\; :2 \\[5pt]
\dfrac{40\cdot 15\,\text{min}}{2}&=& x \\[5pt]
300\,\text{min}&=& x
\end{array}\)](https://mathjax.schullv.de/d8972df46bffc68a77bcfc3dc025624b9c26b5cef5bc66a05f5a35cdae3d8f19?color=5a5a5a) Zwei Mitarbeiter würden für diese Tätigkeit
Zwei Mitarbeiter würden für diese Tätigkeit  benötigen.
benötigen.
c)
Anzahl möglicher Ergebnisse: 
Anzahl günstiger Ergebnisse:
![\(\begin{array}[t]{rll}
& P(\text{grün}) \\[5pt]
=& \dfrac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl möglicher Ergebnisse}} \\[5pt]
=& \dfrac{60\,000}{160\,000} \\[5pt]
=& 37,5\,\%
\end{array}\)](https://mathjax.schullv.de/bfefe028f48a01bc4b305b96ffc135256a4dad81c0fc49dbe6ef176f0c2a84ff?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  ist das erste zufällig herausgefischte Bällchen grün.
ist das erste zufällig herausgefischte Bällchen grün.
Anzahl günstiger Ergebnisse: