Wahlaufgaben

Wahlaufgabe Geometrie

9.1

Auf der Ladefläche eines Lkws steht mittig eine $1,60\,\text{m}$ breite und $1,00\,\text{m}$ hohe Kiste. Diese wird mit einem Spanngurt straff gesichert, der seitlich an der Ladefläche eingehakt wird.

Gelber Lkw mit einer Kiste auf der Ladefläche, Maß von 2,40 m sichtbar.

Skizze nicht maßstäblich

Berechne die Länge, die der Spanngurt mindestens haben muss.

3 BE

9.2

Der Minutenzeiger ist mit $10\,\text{cm}$ doppelt so lang wie der Stundenzeiger. Verbindet man die beiden Zeigerenden, entsteht ein Dreieck.

Skizze nicht maßstäblich

Es ist 8:00 Uhr.

Berechne die Größe aller Innenwinkel dieses Dreiecks.

5 BE

Gib eine Uhrzeit an, zu der das Dreieck den größten Flächeninhalt besitzt. Begründe deine Entscheidung.

2 BE

Wahlaufgabe Funktionen

10.1

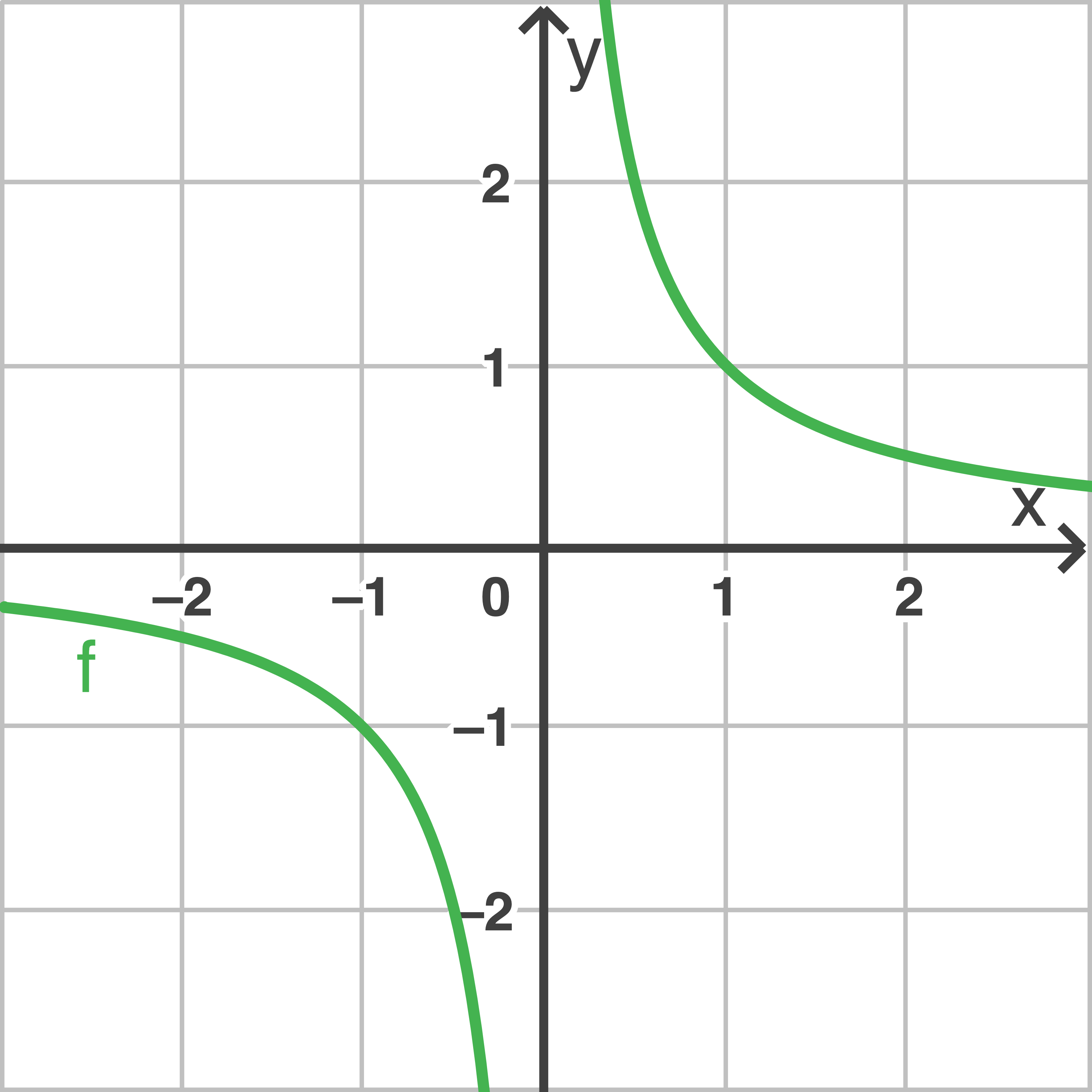
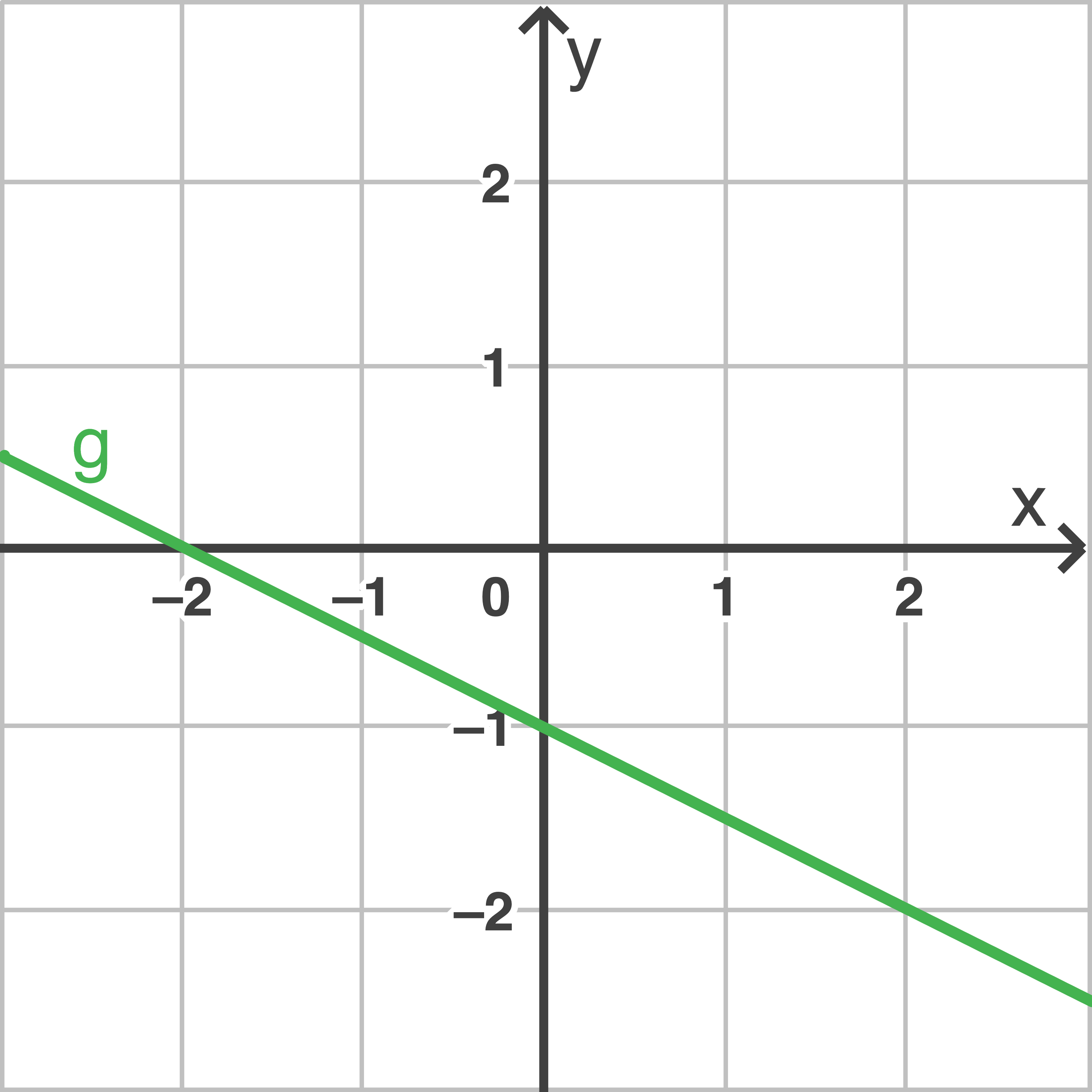
Gib die Funktionsgleichungen der dargestellten Graphen $f \,(x\in\mathbb{R};x\neq0)$ und $g\,(x\in\mathbb{R})$ an.

Graf einer Funktion im Koordinatensystem mit grüner Kurve und Achsenbeschriftungen.

Graph einer linearen Funktion g in einem Koordinatensystem. Die Linie ist grün und fällt von links oben nach rechts unten.

2 BE

10.2

In einem Quiz muss ein Kandidat fünf Fragen beantworten.
Der Kandidat kann eine Möglichkeit für das Quiz auswählen.

Möglichkeit 1:

Es gibt 200 € Startguthaben. Jede richtige Antwort verdoppelt das Guthaben.

Möglichkeit 2:

Jede richtige Antwort bringt 1000 €.

Der Kandidat möchte mit fünf richtig beantworteten Fragen einen möglichst hohen Gewinn erzielen.

Gib die Möglichkeit an, die der Kandidat wählen sollte.
Begründe deine Entscheidung.

4 BE

10.3

Die Flugbahn eines Basketballs kann näherungsweise durch $y=f(x)=ax^2+c \,\,(x\in\mathbb{R})$ beschrieben werden.

Der Ball erreicht eine Maximalhöhe von 4,30 m über dem Boden.

Der Sachverhalt ist in der Skizze dargestellt.

Skizze nicht maßstäblich

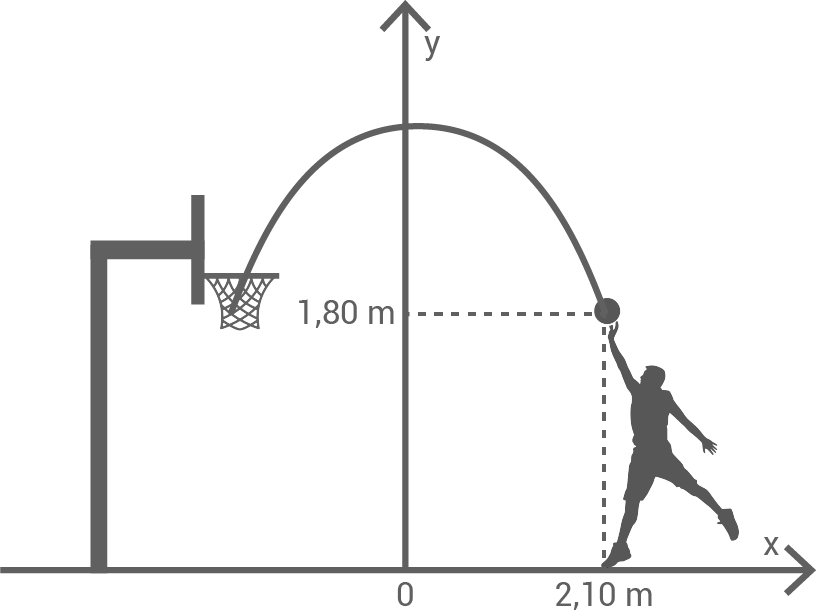Ermittle die Funktionsgleichung für diese Flugbahn.

4 BE

Wahlaufgabe Stochastik

11.1

Die Schülerinnen und Schüler einer Klasse wurden nach dem monatlichen Taschengeld befragt.

Folgende Werte wurden angegeben:

12,00 €	28,00 €
25,00 €	24,00 €
14,00 €	34,00 €
36,00 €	65,00 €
32,00 €	35,00 €
14,00 €	45,00 €
26,00 €	38,00 €
22,00 €	30,00 €

Gib die Spannweite an.

1 BE

Berechne das arithmetische Mittel.

2 BE

Das arithmetische Mittel erhöht sich um 5,00 €. Minimum und Maximum bleiben gleich.

Beschreibe eine Möglichkeit für die Veränderung der Werte.

2 BE

11.2

In einer Verpackung befinden sich Tulpenzwiebeln.
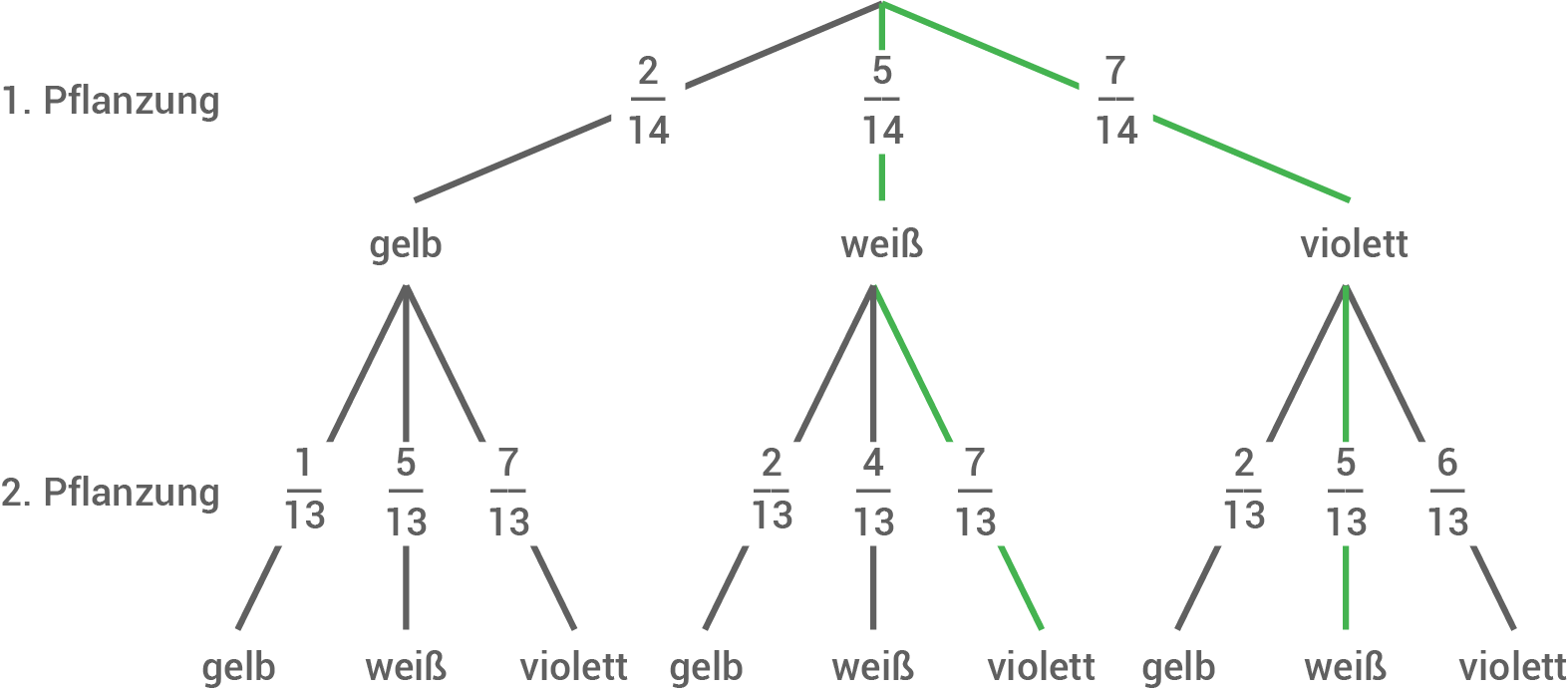
Drei Tulpen blühen gelb, fünf weiß und sieben violett.

Davon wird eine Tulpenzwiebel eingepflanzt.

Gib die Wahrscheinlichkeit dafür an, dass die Tulpe gelb blüht.

2 BE

Die eingepflanzte Tulpenzwiebel blüht gelb.
Von den restlichen Tulpenzwiebeln werden nacheinander zwei Tulpenzwiebeln zufällig ausgewählt und eingepflanzt.

Berechne die Wahrscheinlichkeit dafür, dass eine Tulpe weiß und die andere violett blüht.

3 BE

Wahlaufgabe Arithmetik/Algebra

12.1

Löse folgendes Gleichungssystem $(x, y\in\mathbb{R}).$

$\begin{array}{lrll} \text{I}\quad&y-5&=& 3x &\quad \scriptsize\\ \text{II}\quad&y&=&-\dfrac{1}{2}x+1,5 &\quad \\ \end{array}$

4 BE

12.2

Ein reicher Goldschmied im Mittelalter schrieb in sein Testament:

Meine Frau erbt das gesamte Vermögen von 31 200 Talern, falls wir kinderlos bleiben. Sollte es Kinder geben, bekommt jeder Sohn halb so viel wie die Frau, jede Tochter doppelt so viel wie die Frau.

Als der Goldschmied starb, blieb die Frau mit drei Söhnen und zwei Töchtern zurück.

Berechne die Höhe des Erbes für die Frau, für einen Sohn und für eine Tochter.

4 BE

12.3

Der Marktwert eines junges professionellen Fußballspielers wird mit $4\,850\, €$ angenommen. Bei den erfolgreichsten Fußballspielern verdoppelt sich dieser Marktwert nach jedem Jahr.

Ein international bekannter Fußballspieler hat langjährig erfolgreich bei seinem Verein gespielt und gilt damit als einer der teuersten Spieler der Welt.

Berechne den Marktwert dieses Fußballspielers nach 15 Jahren.

2 BE

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

9.1

Planfigur:

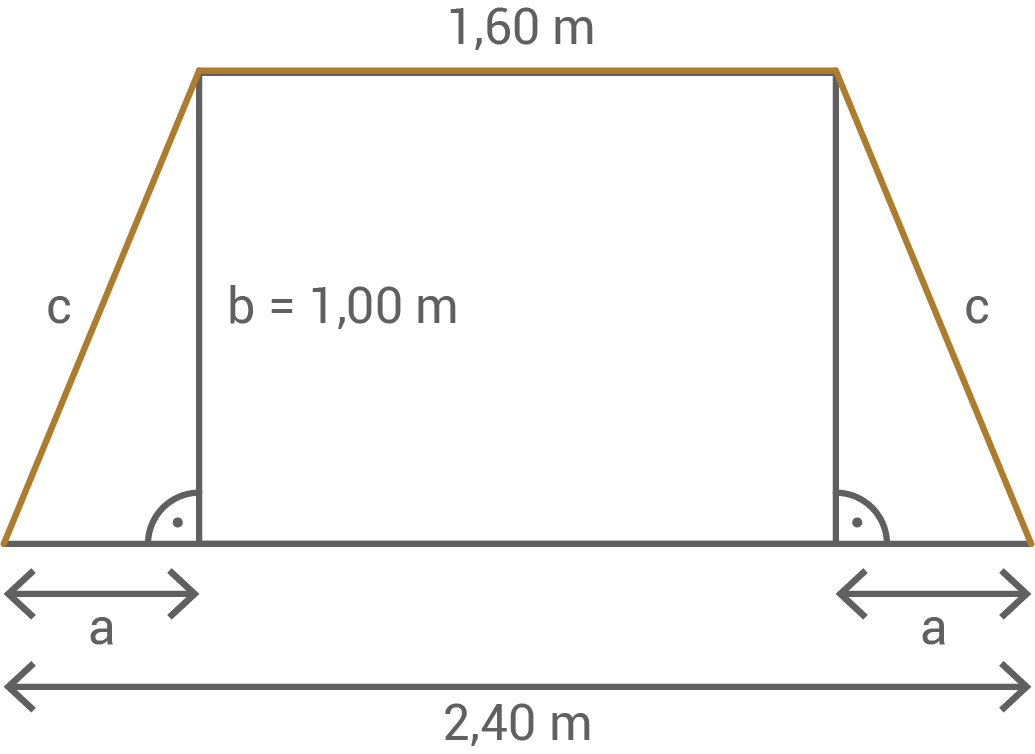Länge der Strecke $a:$

$a=(2,40\,\text{m}-1,60\,\text{m}):2=0,40\,\text{m}$

Länge der Strecke $c$ mit dem Satz des Pythagoras berechnen:

$\begin{array}[t]{rll} c^2&=& a^2+b^2 &\quad \scriptsize \\[5pt] c^2&=&(0,40\,\text{m})^2+ (1,00\,\text{m})^2 &\quad \scriptsize \\[5pt] c^2&=& 1,16 \,\text{m}^2 \quad \scriptsize \mid\; \sqrt{\;} \\[5pt] c&\approx& 1,077\,\text{m} \end{array}$

Damit lässt sich schließlich die Länge des Spanngurts berechnen:

$\begin{array}[t]{rll} \ell&=& 1,60\,\text{m}+ 2 \cdot 1,077\,\text{m} \\[5pt] &\approx& 3,75\,\text{m} \end{array}$

Der Spanngurt muss also mindestens $3,75\,\text{m}$ lang sein.

9.2

Die Uhr ist in 12 Abschnitte von jeweils $\dfrac{360°}{12}=30°$ unterteilt. Der Winkel $\beta$ umfasst 4 Abschnitte und ist daher $4\cdot 30°=120°$ groß.

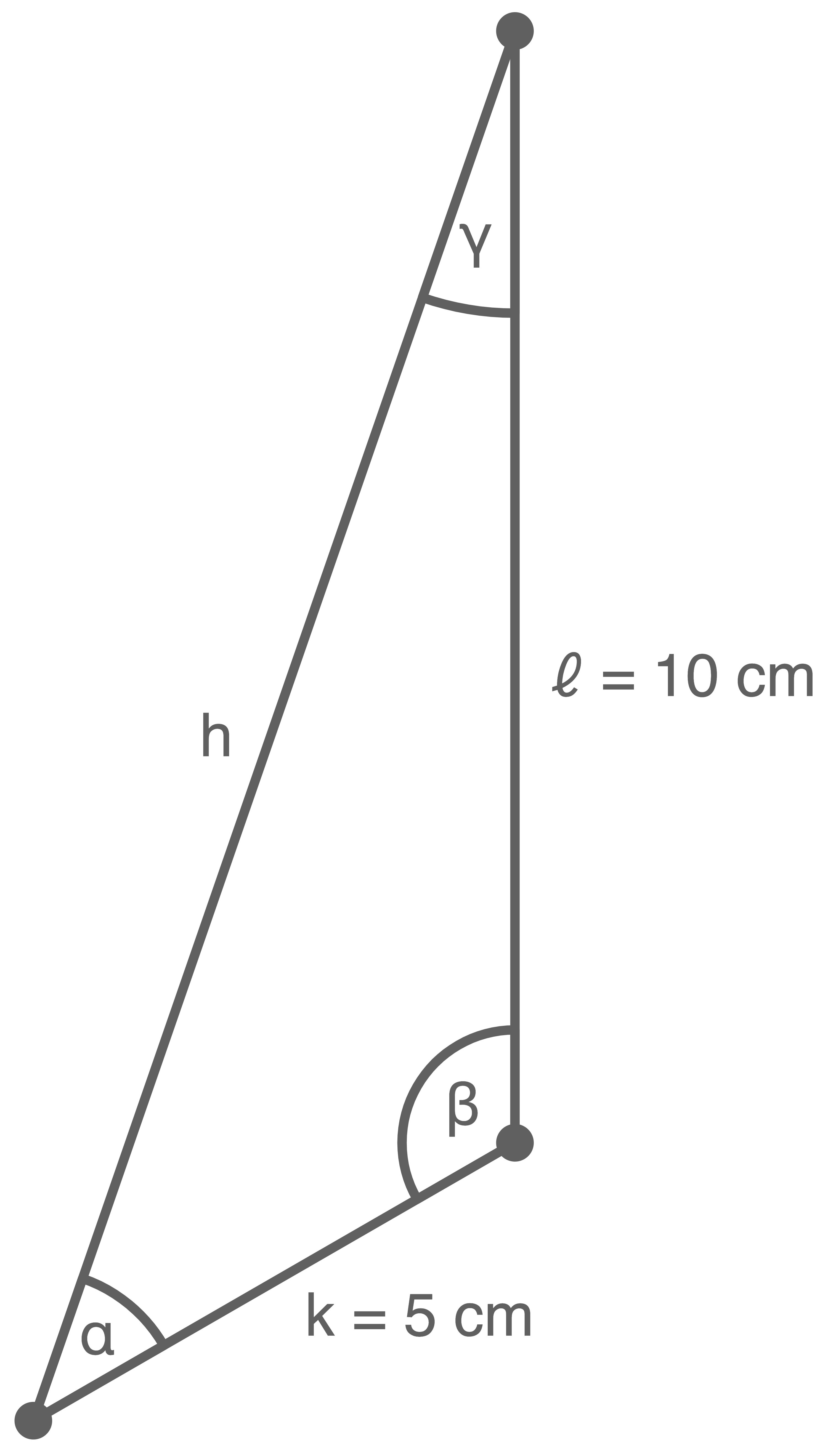Die Länge der Strecke $h$ kann mit dem Kosinussatz berechnet werden:

Rechenweg anzeigen

$h\approx 13,2 \,\text{cm}$

Damit kann die Größe des Winkels $\alpha$ mit dem Sinussatz berechnet werden:

$\begin{array}[t]{rll} \dfrac{\sin(\alpha)}{\ell}&=&\dfrac{\sin(\beta)}{h} \quad \scriptsize \mid\; \cdot\, \ell \\[5pt] \sin(\alpha)&=&\dfrac{\sin(\beta)}{h} \cdot \ell \\[5pt] \sin(\alpha)&=& \dfrac{\sin(120 ^{\circ})}{13,2\,\text{cm}} \cdot 10 \,\text{cm} \\[5pt] \sin(\alpha)&\approx& 0,656 \quad \scriptsize \mid\; \cdot\, \sin^{-1} \\[5pt] \alpha&\approx& 41 ^{\circ} \end{array}$

Mit dem Innenwinkelsummensatz folgt für den Winkel $\gamma:$

$\gamma=180^{\circ}-120^{\circ}-41^{\circ}= 19^{\circ}$

Somit gilt:

$\alpha=41^{\circ}\quad \beta= 120^{\circ} \quad \gamma=19^{\circ}$

Um den Flächeninhalt des Dreiecks zu berechnen, wird folgende Formel verwendet:

$A=\dfrac{1}{2}\cdot k\cdot \ell\cdot \sin \beta$

Der Wert von $\sin \beta$ ist dann am größten, wenn $\beta=90^{\circ}$ gilt. Um 9:00 Uhr bzw. 3:00 Uhr ist der Flächeninhalt somit am größten.

10.1

Die Funktion $f$ muss eine Potenzfunktion mit ungeradem, negativen Exponenten sein.

Vermutete Funktion: $f(x)= \dfrac{1}{x}$

$\color{#ffffff}{x}$	$-2$	$-1$	$1$	$2$
$\color{#ffffff}{y=f(x)}$	$-\dfrac{1}{2}$	$-1$	$1$	$\dfrac{1}{2}$

Die Punkte des Graphen stimmen mit den Werten aus der Wertetabelle überein. Es gilt also:

$y=f(x)=\dfrac{1}{x}$

Die Funktion $g$ ist eine lineare Funktion der Form $y=m\cdot x+n.$

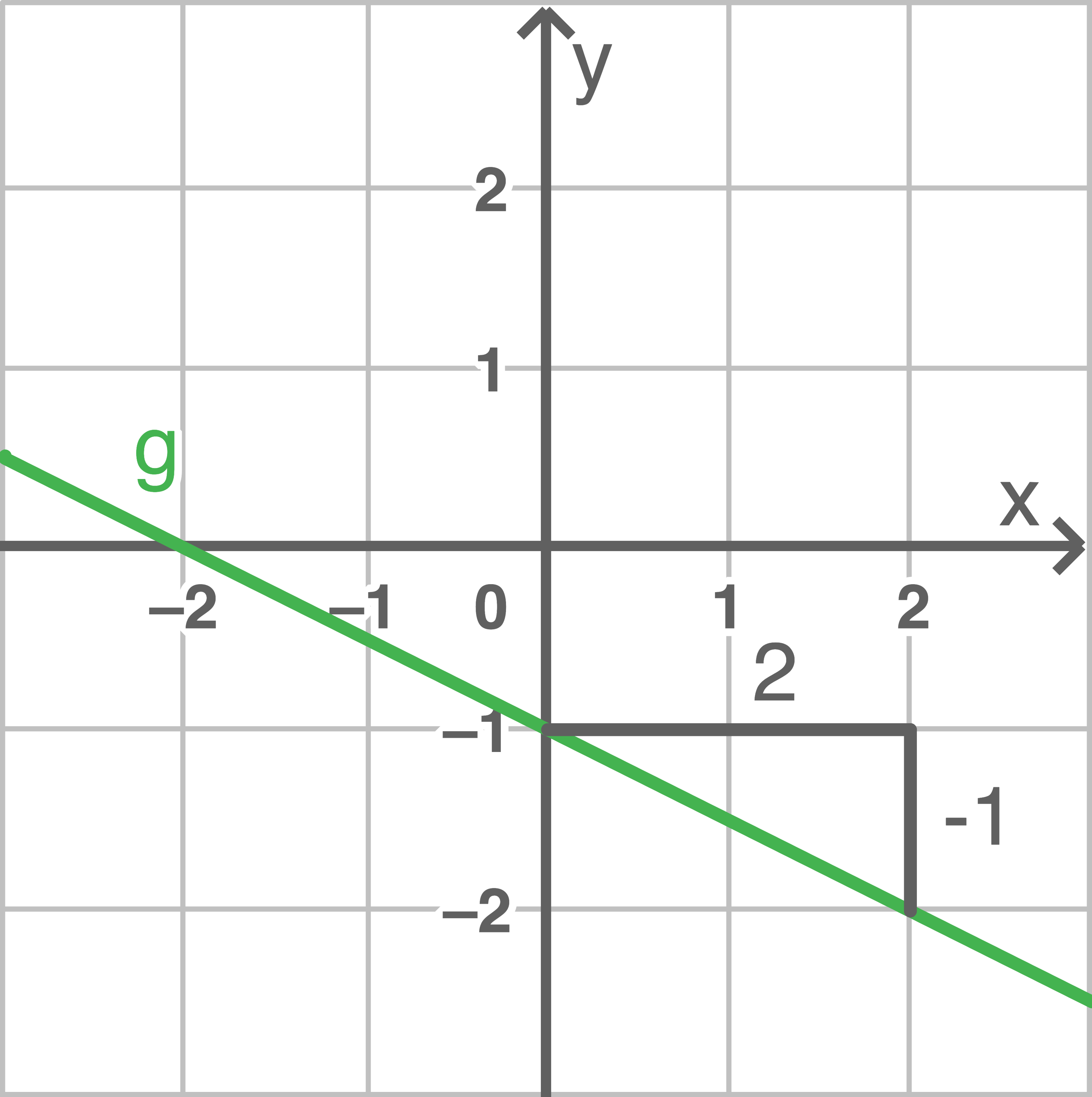Es lässt sich $m=-\dfrac{1}{2}$ und $n=-1$ ablesen. Es folgt:

$y=g(x)= -\dfrac{1}{2}x-1$

10.2

Gewinn bei Möglichkeit 1: $\quad 200\,€ \cdot 2^5= 6\,400\,€$

Gewinn bei Möglichkeit 2: $\quad 1\,000\,€ \cdot 5= 5\,000\,€$

Wegen $6\,400\,€ \gt 5\,000\,€$ sollte der Kandidat die 1. Möglichkeit wählen.

10.3

Die Maximalhöhe von $4,30\,\text{m}$ wird am Scheitelpunkt der Parabel erreicht. Dieser liegt auf der $y$ -Achse. Es gilt also $c=3,4$ und die Funktionsgleichung ist von der Form $y=f(x)=ax^2+4,3.$

Der Wert von $a$ wird mit den Koordinaten des Punktes $P(2,1\mid 1,8)$ der Startposition des Balles berechnet:

$\begin{array}[t]{rll} y&=& a\cdot x^2+4,3 \\[5pt] 1,8&=& a \cdot (2,1)^2 +4,3\quad \scriptsize \mid\; -4,3\\[5pt] -2,5&=& a \cdot (2,1)^2 \quad \scriptsize \mid\; :(2,1)^2\\[5pt] -0,57 &\approx & a \end{array}$

Daraus ergibt sich:

$y=f(x)= -0,57x^2+4,3$

11.1

$\begin{array}[t]{rll} R&=&x_{\text{max}} – x_{\text{min}} \\[5pt] &=&65,00\,€ - 12,00\,€ \\[5pt] &=&53,00\,€ \end{array}$

Die Spannweite beträgt $53,00\,€.$

Anzahl der Werte: $16$

Summe der Werte:
$12\,€+25\,€$ $+14\,€$ $+36\,€$ $+32\,€$ $+14\,€$ $+26\,€$ $+22\,€$ $+28\,€$ $+24\,€$ $+34\,€$ $+65\,€$ $+35\,€$ $+45\,€$ $+38\,€$ $+30\,€$
$=480\,€$

$\begin{array}[t]{rll} \overline{x}&=& \dfrac{\text{Summe der Werte}}{\text{Anzahl der Werte}} \\[5pt] &=& \dfrac{480\,€}{16} \\[5pt] &=& 30,00 \,€ \end{array}$

$\overline{x}_\text{neu}=30\,€+5\,€=35\,€$

$s:$ Wert, der zur Taschengeldsumme hinzukommen muss

$\begin{array}[t]{rll} 35 \,€&=&\dfrac{480 \,€ +s}{16} \quad \scriptsize \mid\; \cdot 16 \\[5pt] 35 \,€ \cdot 16&=& 480 \,€ + s \quad \scriptsize \mid\; - 480 \,€ \\[5pt] 560 \,€ - 480 \,€ &=& s \\[5pt] 80 \,€ &=& s \end{array}$

Diese $80 \,€$ müssen nun auf die einzelnen Taschengelder verteilt werden. Das Minimum und Maximum dürfen dabei nicht geändert werden. Zum Beispiel könnten von den restlichen 14 Werten 10 Taschengelder um $8 \,€$ erhöht werden.

11.2

15 mögliche Ergebnisse: $3+5+7$
3 günstige Ergebnisse

$\begin{array}[t]{rll} & P(\text{Tulpe blüht gelb})\\[5pt] =& \dfrac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl möglicher Ergebnisse}} \\[5pt] =& \dfrac{3}{15} \\[5pt] =& \dfrac{1}{5} \end{array}$

Die Wahrscheinlichkeit, dass eine Tulpe gelb blüht, beträgt $\dfrac{1}{5}=20\,\%.$

$\begin{array}[t]{rll} &P(\text{weiß, violett})\\[5pt] &=\dfrac{5}{14}\cdot \dfrac{7}{13}+\dfrac{7}{14}\cdot \dfrac{5}{13} \\[5pt] &=\dfrac{5}{2}\cdot \dfrac{1}{13}+\dfrac{1}{2}\cdot \dfrac{5}{13} \\[5pt] &=\dfrac{5}{26}+\dfrac{5}{26} \\[5pt] &=\dfrac{10}{26} \\[5pt] &=\dfrac{5}{13} \end{array}$

Die Wahrscheinlichkeit für eine weiße und eine violette Tulpe liegt also bei $\dfrac{5}{13}\approx 38 \,\%.$

12.1

$\begin{array}{lrll} \text{I}\quad&y-5&=& 3x &\quad \scriptsize\\ \text{II}\quad&y&=&-\dfrac{1}{2}x+1,5 &\quad \\ \end{array}$

Es bietet sich das Einsetzungsverfahren an.

$\text{II}$ in $\text{I}:$

$\begin{array}[t]{rll} -\dfrac{1}{2}x+1,5-5&=& 3x \quad \scriptsize \mid\; + \dfrac{1}{2}x \\[5pt] -3,5&=& 3,5x \quad \scriptsize \mid\; :3,5 \\[5pt] -1&=& x \end{array}$

Einsetzen von $x=-1$ in $\text{II}:$

$y=-\dfrac{1}{2}\cdot (-1)+1,5=2$

Das Gleichungssystem hat die Lösung $x=-1$ und $y=2.$

12.2

Erbe der Frau: $x$
Erbe der Töchter: je $2x$
Erbe der Söhne: je $0,5x$

$\begin{array}[t]{rll} x+2\cdot 2x+3\cdot 0,5x&=& 31\,200\,€ \\[5pt] 6,5x&=& 31\,200\,€ \quad \scriptsize \mid\; : 6,5\\[5pt] x &=& 4\,800\,€ \end{array}$

Erbe der Frau: $4\,800\,€$
Erbe einer Tochter : $2\cdot 4\,800\,€= 9\,600\,€$
Erbe eines Sohnes : $0,5\cdot 4\,800\,€ = 2\,400\,€$

12.3

Es handelt sich um exponentielles Wachstum.

Anfangswert: $W_0=4\,580\,€$

Jährliche Verdopplung: $q=2$

Anzahl der Jahre: $n=15$

Mit der Wachstumsformel $W_n=W_0\cdot q^n$ kann der Marktwert nach 15 Jahren berechnet werden:

$\begin{array}[t]{rll} W_{15}&=& 4\,580\,€\cdot 2^{15}\\[5pt] &=& 150\,077\,440\,€ \end{array}$

Nach 15 Jahren hat der Fußballer einen Marktwert von $150\,077\,440\,€.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?