Pflichtaufgaben
1
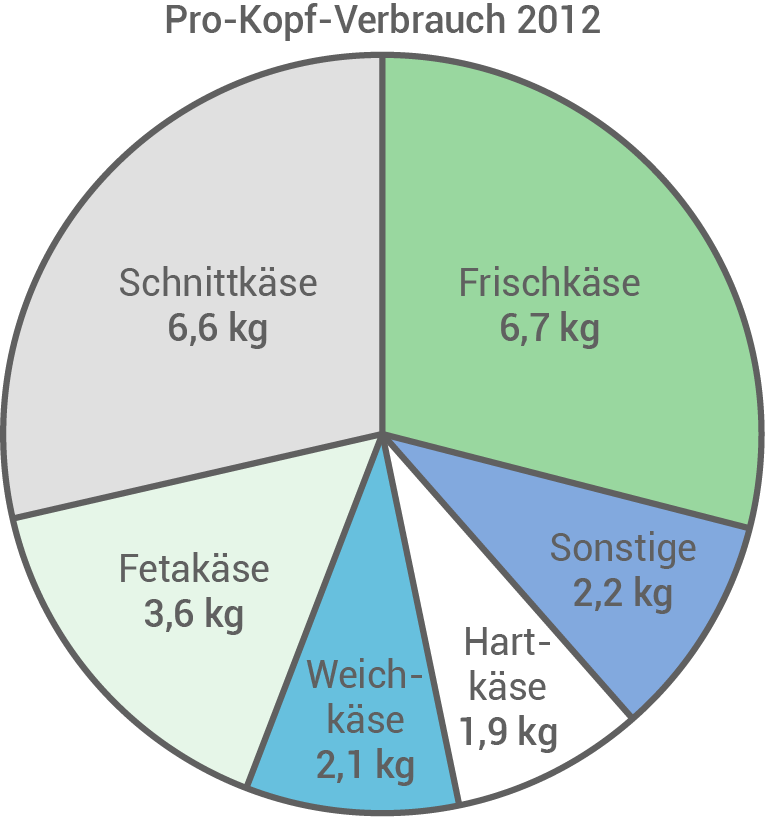
In dem Diagramm ist der Pro-Kopf-Verbrauch von Käse in Deutschland aus dem Jahr 2012 dargestellt.
 angestiegen.
angestiegen.


a)
Berechne den prozentualen Anteil von Hartkäse am gesamten Pro-Kopf-Verbrauch von Käse im Jahr 2012.
Der Pro-Kopf-Verbrauch von Frischkäse ist vom Jahr 2000 bis zum Jahr 2012 um
1 BE
b)
Berechne den Pro-Kopf-Verbrauch von Frischkäse für das Jahr 2000.
Der Pro-Kopf-Verbrauch von Schnittkäse steigt jährlich etwa um
2 BE
c)
Berechne den voraussichtlichen Pro-Kopf-Verbrauch von Schnittkäse im Jahr 2015.
1 BE
2
Die Pilatusbahn in der Schweiz ist die steilste Zahnradbahn der Welt. Sie beginnt an der Station Alpnachstad ( ü. NN) und endet nach
ü. NN) und endet nach  an der Station Pilatus Kulm (
an der Station Pilatus Kulm ( ü. NN).
Berechne den durchschnittlichen Anstiegswinkel der Pilatusbahn von Alpnachstad nach Pilatus Kulm.
ü. NN).
Berechne den durchschnittlichen Anstiegswinkel der Pilatusbahn von Alpnachstad nach Pilatus Kulm.
2 BE
3
Ein Kegel hat einen Radius von  und ist
und ist  hoch.
hoch.
 hoch und hat den Radius
hoch und hat den Radius  . Sein Volumen ist sechsmal so groß wie das Volumen eines Kegels mit dem gleichen Radius.
. Sein Volumen ist sechsmal so groß wie das Volumen eines Kegels mit dem gleichen Radius.
a)
Berechne den Oberflächeninhalt dieses Kegels.
Ein Zylinder ist
2 BE
b)
Ermittle die Höhe des Kegels.
1 BE
4
Gegeben ist die Funktion  mit
mit  .
.
 verläuft durch den Scheitelpunkt
verläuft durch den Scheitelpunkt  der Funktion
der Funktion  und durch den Punkt
und durch den Punkt  .
.
a)
Stelle diese Funktion in einem Koordinatensystem grafisch dar und berechne die Nullstellen von  .
.
Der Graph einer linearen Funktion
2 BE
b)
Gib die Funktionsgleichung von  an.
an.
1 BE
5
In einem Dreieck ist die längste Seite  lang.
lang.
Eine weitere Seite hat eine Länge von .
.
Ein Innenwinkel ist groß.
Berechne die Länge der dritten Seite.
groß.
Berechne die Länge der dritten Seite.
Eine weitere Seite hat eine Länge von
Ein Innenwinkel ist
2 BE
6
Löse die Gleichung.

2 BE
7
In einem Behälter sind insgesamt 18 Kugeln.
Es sind rote und blaue Kugeln.
Die Wahrscheinlichkeit für das Ziehen einer roten Kugel beträgt .
.
Es sind rote und blaue Kugeln.
Die Wahrscheinlichkeit für das Ziehen einer roten Kugel beträgt
a)
Gib die Anzahl der roten Kugeln an.
1 BE
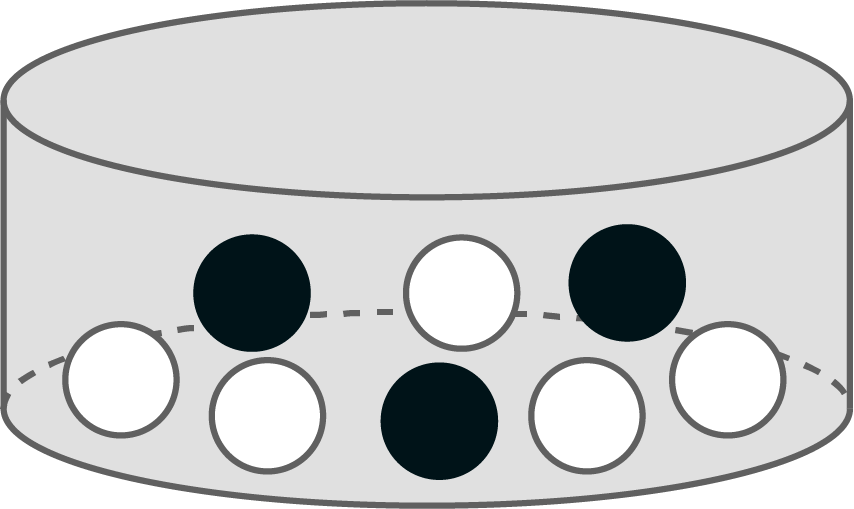
In einem anderen Behälter (siehe Abbildung) befinden sich weiße und schwarze Kugeln.

b)
Gib die Wahrscheinlichkeit für das Ziehen einer weißen Kugel an.
1 BE
c)
Wie groß ist die Wahrscheinlichkeit, beim zweimaligen Ziehen ohne Zurücklegen, zwei schwarze Kugeln zu ziehen.
1 BE
8
Die Länge einer unzugänglichen Strecke  im Gelände soll bestimmt werden.
im Gelände soll bestimmt werden.
Dazu wurden die in der Skizze angegebenen Werte ermittelt.
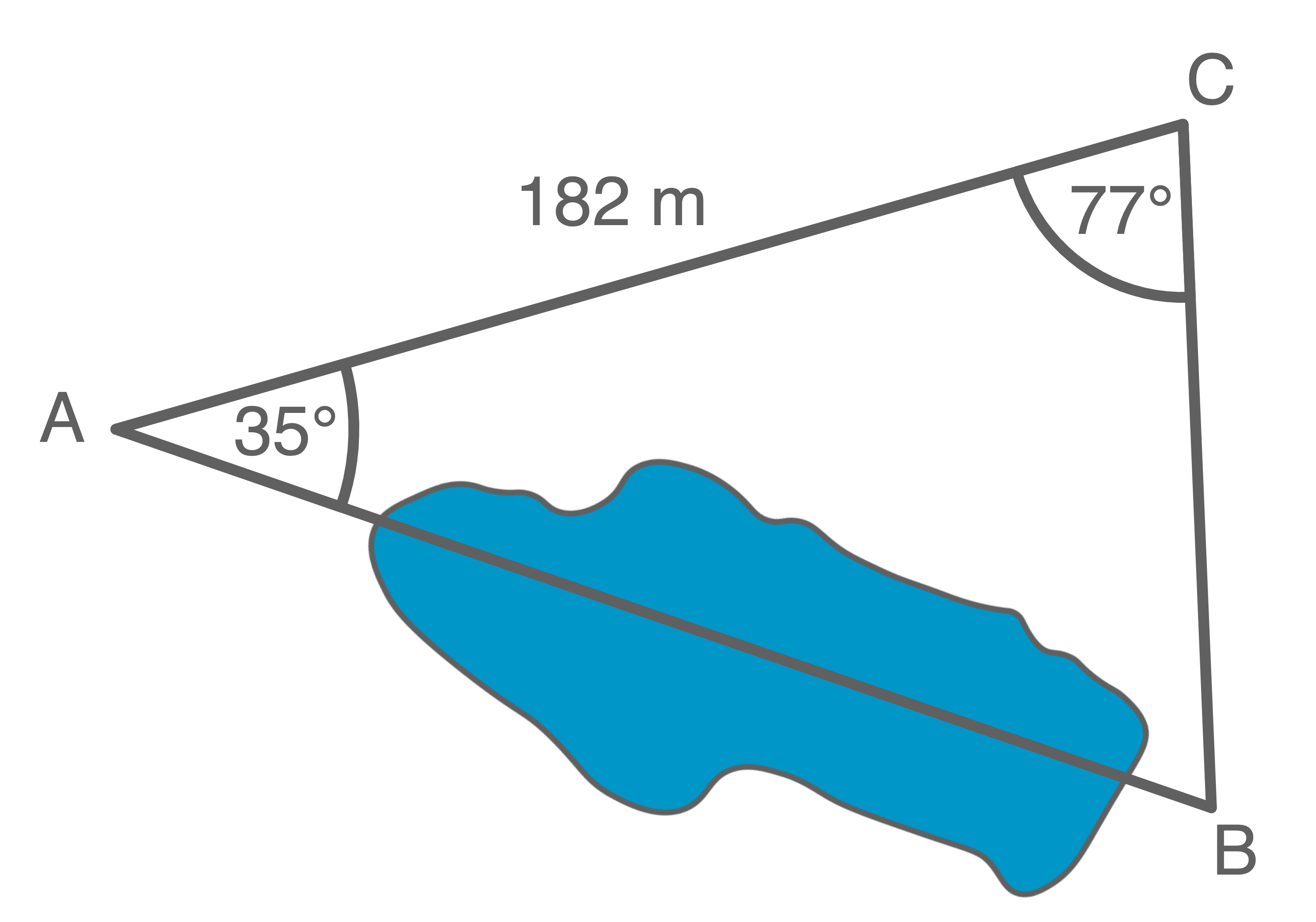
Vier Schüler einer 10. Klasse haben durch Konstruktion für die Länge der Strecke Dazu wurden die in der Skizze angegebenen Werte ermittelt.

Skizze nicht maßstäblich
a)
Berechne die Länge der Strecke 
2 BE
b)
Um wie viele Meter weicht die berechnete Länge der Strecke  vom Mittelwert der Schülerergebnisse ab?
vom Mittelwert der Schülerergebnisse ab?
1 BE
c)
Zeichne das Dreieck  im Maßstab
im Maßstab  .
.
2 BE
1
a)
Lösung mit Lösungsformel
 Der Prozentsatz
Der Prozentsatz  lässt sich wie folgt berechnen:
lässt sich wie folgt berechnen:
![\(\begin{array}[t]{rll}
p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt]
p\,\%&=& \dfrac{1,9\,\text{kg}}{23,1\,\text{kg}}\cdot 100\,\% \\[5pt]
p\,\%&\approx& 8,2\,\%
\end{array}\)](https://mathjax.schullv.de/1f49c1ca2d1bd7a65b3dc3b37b8e0af1c6823121d9eabe397845f274674f505c?color=5a5a5a) Lösung mit Dreisatz
Lösung mit Dreisatz




![\(\begin{array}{rcl}
23,1\,\text{kg} & \mathrel{\widehat{=}}& 100\,\%\\[5pt]
1\,\text{kg} & \mathrel{\widehat{=}}& \dfrac{100}{23,1}\,\%\\[5pt]
1,9\,\text{kg} & \mathrel{\widehat{\approx}}& 8,2\,\%
\end{array}\)](https://mathjax.schullv.de/14cc0f4859e098ff0bd9452328e3a5efcdfcb3dce86e2dac26670f45dddb16dd?color=5a5a5a)



 Der prozentuale Anteil von Hartkäse beträgt ungefähr 8,2 %.
Der prozentuale Anteil von Hartkäse beträgt ungefähr 8,2 %.
b)
Lösung mit Lösungsformel

 Der Grundwert
Der Grundwert  lässt sich wie folgt berechnen:
lässt sich wie folgt berechnen:
![\(\begin{array}[t]{rll}
G&=& \dfrac{W\cdot 100\,\%}{p\,\%} \\[5pt]
G&=& \dfrac{6,7\,\text{kg}\cdot 100\,\%}{128,8\,\%} \\[5pt]
G&\approx& 5,2\,\text{kg}
\end{array}\)](https://mathjax.schullv.de/70497fdbf425e0bf5fe634fd567712e80d61e09728b0845388cd00857b1d7b9a?color=5a5a5a) Lösung mit Dreisatz
Lösung mit Dreisatz




![\(\begin{array}{rcl}
128,8\,\% & \mathrel{\widehat{=}}& 6,7\,\text{kg}\\[5pt]
1\,\% & \mathrel{\widehat{=}}& \dfrac{6,7}{128,8}\,\text{kg}\\[5pt]
100\,\% & \mathrel{\widehat{\approx}}& 5,2\,\text{kg}
\end{array}\)](https://mathjax.schullv.de/40a0c1cbf79185e68ccaa7daa1afb147332b2485bb9a6a32c4f0aeebcf8543a3?color=5a5a5a)



 Der Pro-Kopf-Verbrauch von Frischkäse lag im Jahr 2000 bei etwa
Der Pro-Kopf-Verbrauch von Frischkäse lag im Jahr 2000 bei etwa 
c)
2
Skizze des Sachverhalts:
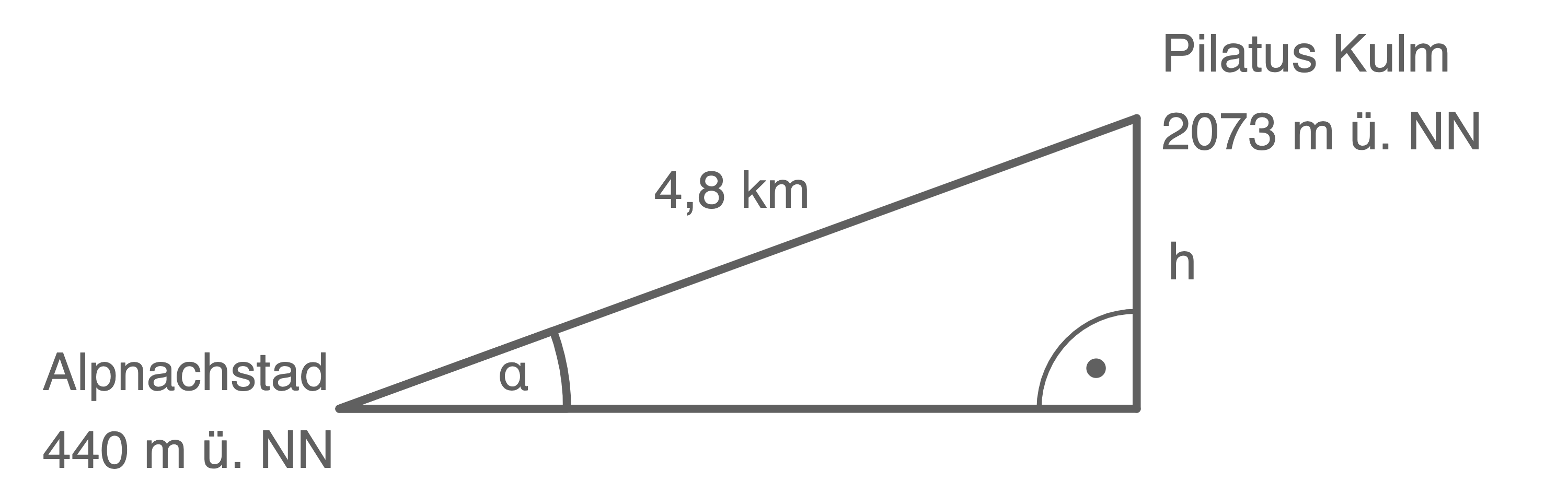 Um den Winkel
Um den Winkel  zu berechnen muss zunächst der Höhenunterschied
zu berechnen muss zunächst der Höhenunterschied  berechnet werden:
berechnet werden:
 Damit folgt:
Damit folgt:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}\\[5pt]
\sin(\alpha)&=&\dfrac{1\,633\,\text{m}}{4\,800\,\text{m}}\quad\scriptsize\mid\; \sin^{-1}\\[5pt]
\alpha&\approx& 20^{\circ}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/70e24ca1d533adca9793c56b1892c2dd45f5d51d11dea16a286f316af681ab27?color=5a5a5a) Die Größe des durchschnittlichen Steigungswinkels beträgt etwa
Die Größe des durchschnittlichen Steigungswinkels beträgt etwa 

3
a)
Der Oberflächeninhalt eines Kegels lässt sich mit der Formel  berechnen.
berechnen.
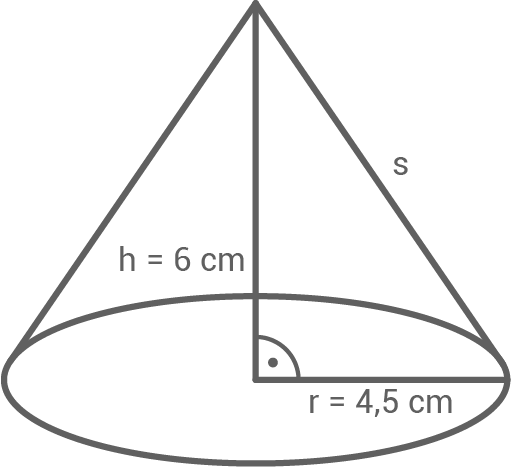 Die Länge der Seite
Die Länge der Seite  kann mit dem Satz des Pythagoras bestimmt werden:
kann mit dem Satz des Pythagoras bestimmt werden:
![\(\begin{array}[t]{rll}
s^2&=& r^2+h^2\quad \mid\;\scriptsize \sqrt{\;}\\[5pt]
s&=& \sqrt{r^2+h^2}\\[5pt]
s&=& \sqrt{(4,5\,\text{cm})^2+(6\,\text{cm})^2}\\[5pt]
s&=& 7,5\,\text{cm}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/a54e3a233157990272206bcfda4cbbf5727c73a0d76c138d20eaabdea4bcfa2a?color=5a5a5a) Die Seite
Die Seite  ist 7,5 cm lang. Jetzt kann der Oberflächeninhalt bestimmt werden:
ist 7,5 cm lang. Jetzt kann der Oberflächeninhalt bestimmt werden:
![\(\begin{array}[t]{rll}
A_{\text{Kegel}}&=& \pi \cdot r^2 + \pi \cdot r \cdot s\\[5pt]
&=& \pi \cdot (4,5\,\text{cm})^2 + \pi \cdot 4,5\,\text{cm} \cdot 7,5\,\text{cm}\\[5pt]
&\approx& 63,6\,\text{cm}^2+106\,\text{cm}^2\\[5pt]
&\approx& 170\,\text{cm}^2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/09f594900d7fef6213ee3515411149c03ef657bf07f344e3f4497cd24f198f38?color=5a5a5a) Der Oberflächeninhalt beträgt ungefähr
Der Oberflächeninhalt beträgt ungefähr  .
.

b)
Das Zylindervolumen ist gegeben durch:
 Für das Kegelvolumen gilt:
Für das Kegelvolumen gilt:
 Da der Zylinder das sechsfache Volumen des Kegels mit dem gleichen Radius hat, gilt:
Da der Zylinder das sechsfache Volumen des Kegels mit dem gleichen Radius hat, gilt:
![\(\begin{array}[t]{rll}
V_Z&=& 6\cdot V_K \\[5pt]
\pi\cdot r^2\cdot 10\,\text{cm}&=& 6\cdot \dfrac{1}{3}\cdot \pi\cdot r^2\cdot h_K \quad \scriptsize \mid\; :\pi \cdot r^2\\[5pt]
10\,\text{cm}&=& 2\cdot h_K \quad \scriptsize \mid\; :2 \\[5pt]
5\,\text{cm}&=& h_K
\end{array}\)](https://mathjax.schullv.de/1818b7c6399c340cde8075338d6d87ec2059d1706cdce7caa05062acf130d86f?color=5a5a5a) Der Kegel ist 5 cm hoch.
Der Kegel ist 5 cm hoch.
4
a)
Graphen von  grafisch darstellen
grafisch darstellen
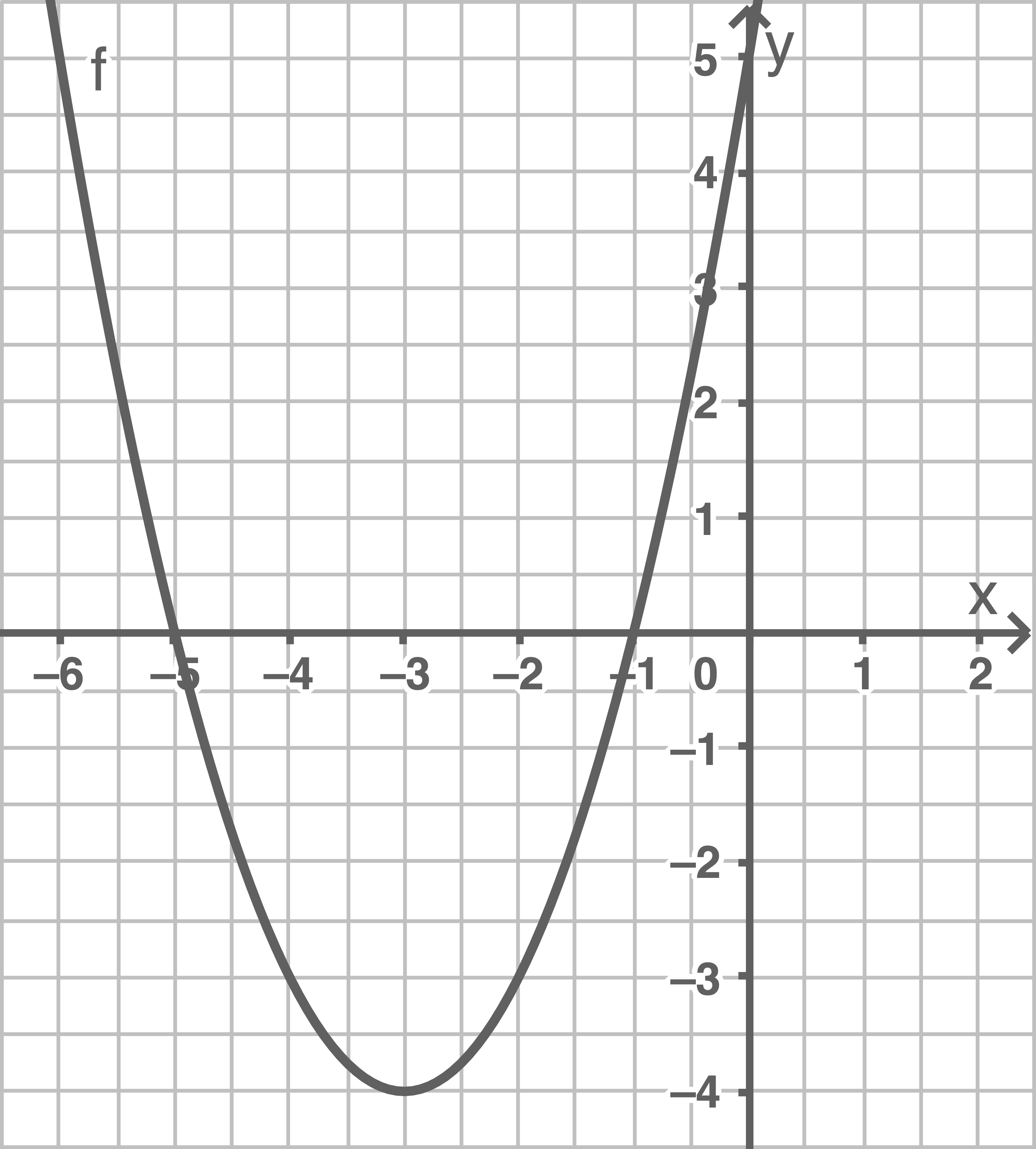 Nullstellen von
Nullstellen von  berechnen
Funktion gleich 0 setzen:
berechnen
Funktion gleich 0 setzen:
![\(\begin{array}[t]{rll}
y=f(x)&=& x^2+6x+5 \\[5pt]
0&=& x^2+6x+5
\end{array}\)](https://mathjax.schullv.de/d54da0d714481d63e5ff431694f1b60e265158fc95ff953f5a0849b0213aa191?color=5a5a5a) Es gilt
Es gilt  und
und  Mit der Lösungsformel folgt:
Mit der Lösungsformel folgt:
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{p}{2}\pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
x_{1/2}&=& -\dfrac{6}{2}\pm \sqrt{\left(\dfrac{6}{2}\right)^2-5} \\[5pt]
x_{1/2}&=& -3\pm \sqrt{4} \\[5pt]
x_{1/2}&=& -3\pm 2 \\[5pt]
x_1&=& -1 \\[5pt]
x_2&=& -5
\end{array}\)](https://mathjax.schullv.de/bccd545570cc85cd370c021786010a86cb826a6352b659d173ff8285cae940b5?color=5a5a5a) Die Funktion
Die Funktion  hat die Nullstellen
hat die Nullstellen  und
und 
Beim Graphen der Funktion  handelt es sich um eine verschobene Normalparabel. Um diese grafisch darstellen zu können, wird der Scheitelpunkt berechnet:
handelt es sich um eine verschobene Normalparabel. Um diese grafisch darstellen zu können, wird der Scheitelpunkt berechnet:
 Es gilt
Es gilt  und
und 




b)
Grafische Lösung
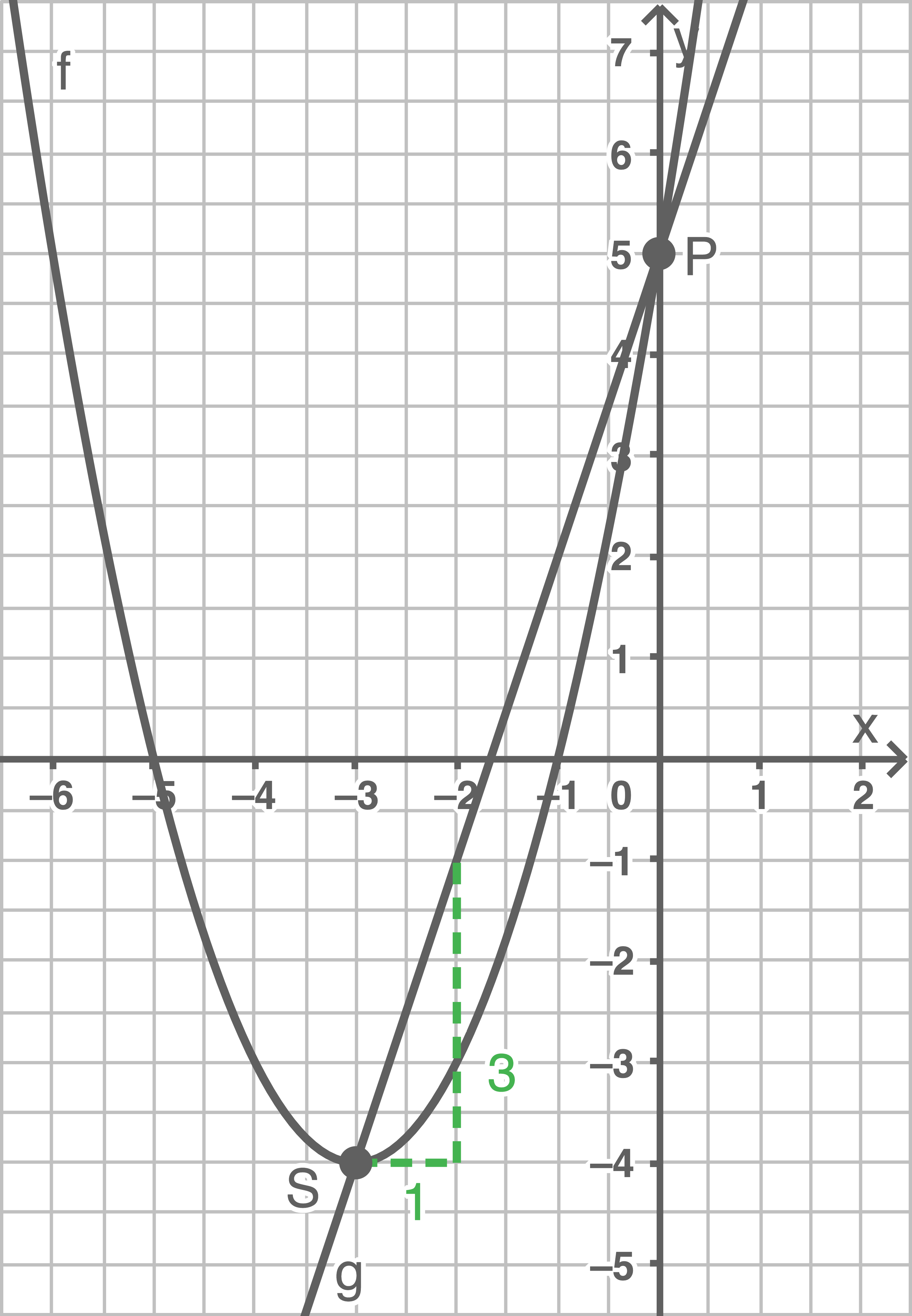
![\(\begin{array}[t]{rll}
m&=&\dfrac{y_P-y_S}{x_P-x_S}\\[5pt]
&=&\dfrac{5-(-4)}{0-(-3)}\\[5pt]
&=&3\\[5pt]
\end{array}\)](https://mathjax.schullv.de/8c49ce71182df590f22926a09c5578cca6bb4b87b0eb126d3118204344270cc4?color=5a5a5a) Die Funktion ist also von der Form
Die Funktion ist also von der Form  Einsetzen der Koordinaten des Punktes
Einsetzen der Koordinaten des Punktes  liefert:
liefert:
![\(\begin{array}[t]{rll}
5&=& 3\cdot 0+n \\[5pt]
5&=& n
\end{array}\)](https://mathjax.schullv.de/2f100d5af3a0c9ce49ba8d118888607ac69e564bdf2951b5f9b81ddd97943cf0?color=5a5a5a) Die Funktionsgleichung lautet:
Die Funktionsgleichung lautet:


Aus der grafischen Darstellung lassen sich die folgenden Werte ablesen:
 -Achsenabschnitt:
-Achsenabschnitt:  Steigung:
Steigung:  Damit ergibt sich folgende Funktionsgleichung:
Damit ergibt sich folgende Funktionsgleichung:

Rechnerische Lösung
Die Steigung der Funktion lässt sich wie folgt berechnen:
5
Die Winkelsumme im Dreieck ist  , daher kann es keinen weiteren Winkel größer als
, daher kann es keinen weiteren Winkel größer als  geben. Die Seite
geben. Die Seite  ist die längste Seite des Dreiecks und muss daher gegenüber des größten Winkels liegen.
ist die längste Seite des Dreiecks und muss daher gegenüber des größten Winkels liegen.
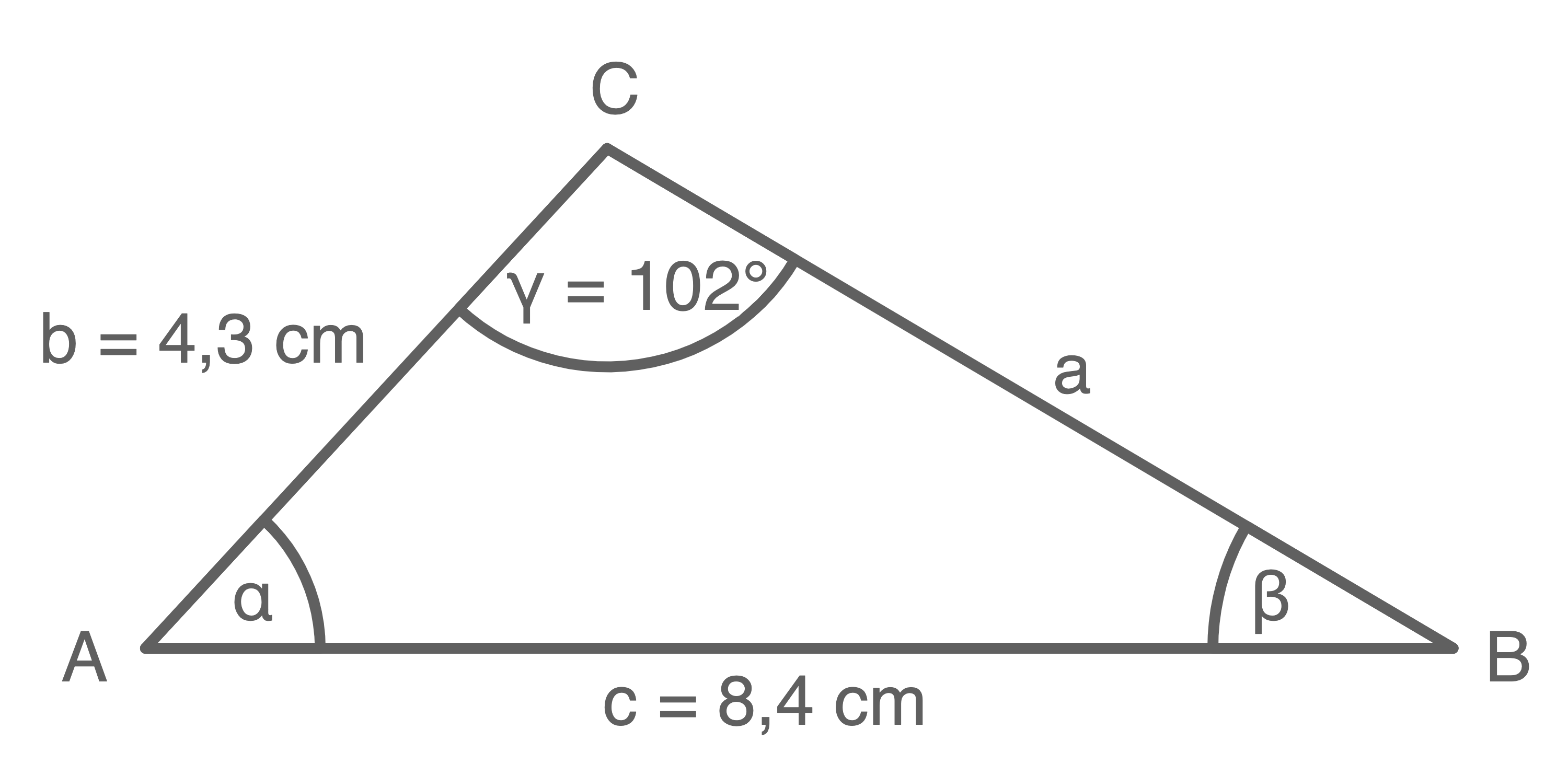 Der Winkel
Der Winkel  lässt sich mit dem Sinussatz berechnen:
lässt sich mit dem Sinussatz berechnen:
![\(\begin{array}[t]{rll}
\dfrac{b}{\sin \beta}&=& \dfrac{c}{\sin \gamma} \quad \scriptsize \mid\; \cdot \sin \beta\\[5pt]
b&=& \dfrac{c}{\sin \gamma}\cdot \sin \beta \quad \scriptsize \mid\; :\dfrac{c}{\sin \gamma}\\[5pt]
\dfrac{b\cdot \sin \gamma}{c}&=& \sin\beta \\[5pt]
\dfrac{4,3\,\text{cm}\cdot \sin 102°}{8,4\,\text{cm}}&=& \sin\beta \quad \scriptsize \mid\; \sin^{-1}\\[5pt]
30°&\approx& \beta
\end{array}\)](https://mathjax.schullv.de/c76246eee3478bcea5fae46328654a276643fee783a836d7cd8cad22d6304da9?color=5a5a5a) Mit der Innenwinkelsumme des Dreiecks lässt sich nun der Winkel
Mit der Innenwinkelsumme des Dreiecks lässt sich nun der Winkel  berechnen:
berechnen:
 Die Länge der dritten Seite
Die Länge der dritten Seite  lässt sich mit dem Sinussatz wie folgt berechnen:
lässt sich mit dem Sinussatz wie folgt berechnen:
![\(\begin{array}[t]{rll}
\dfrac{a}{\sin \alpha}&=& \dfrac{c}{\sin \gamma} \quad \scriptsize \mid\; \cdot \sin \alpha \\[5pt]
a&=& \dfrac{\sin \alpha\cdot c}{\sin \gamma} \\[5pt]
a&=& \dfrac{\sin 48°\cdot 8,4\,\text{cm}}{\sin 102°} \\[5pt]
a&\approx& 6,4\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/730cadac9eb817eb992439f89455d18b9d5929de0c45d42ec3fcddbfd0151e7f?color=5a5a5a) Die dritte Seite ist ungefähr 6,4 cm lang.
Die dritte Seite ist ungefähr 6,4 cm lang.

Skizze
6
7
a)
b)
Die Wahrscheinlichkeit, eine weiße Kugel zu ziehen, beträgt 
c)
Da es sich um Ziehen ohne Zurücklegen handelt, gilt mit der Pfadmultiplikationsregel:
![\(\begin{array}[t]{rll}
P(\text{zweimal schwarz})&=& \dfrac{3}{8}\cdot \dfrac{2}{7} \\[5pt]
&=& \dfrac{3}{28}
\end{array}\)](https://mathjax.schullv.de/1a0764d0974b09aa557705eb7bacb8d40a123aa591bf5e69acf965a691733a33?color=5a5a5a) Die Wahrscheinlichkeit für zwei schwarze Kugeln beträgt
Die Wahrscheinlichkeit für zwei schwarze Kugeln beträgt 
8
a)
Die Größe des Winkels  kann mit der Innenwinkelsumme berechnet werden:
kann mit der Innenwinkelsumme berechnet werden:

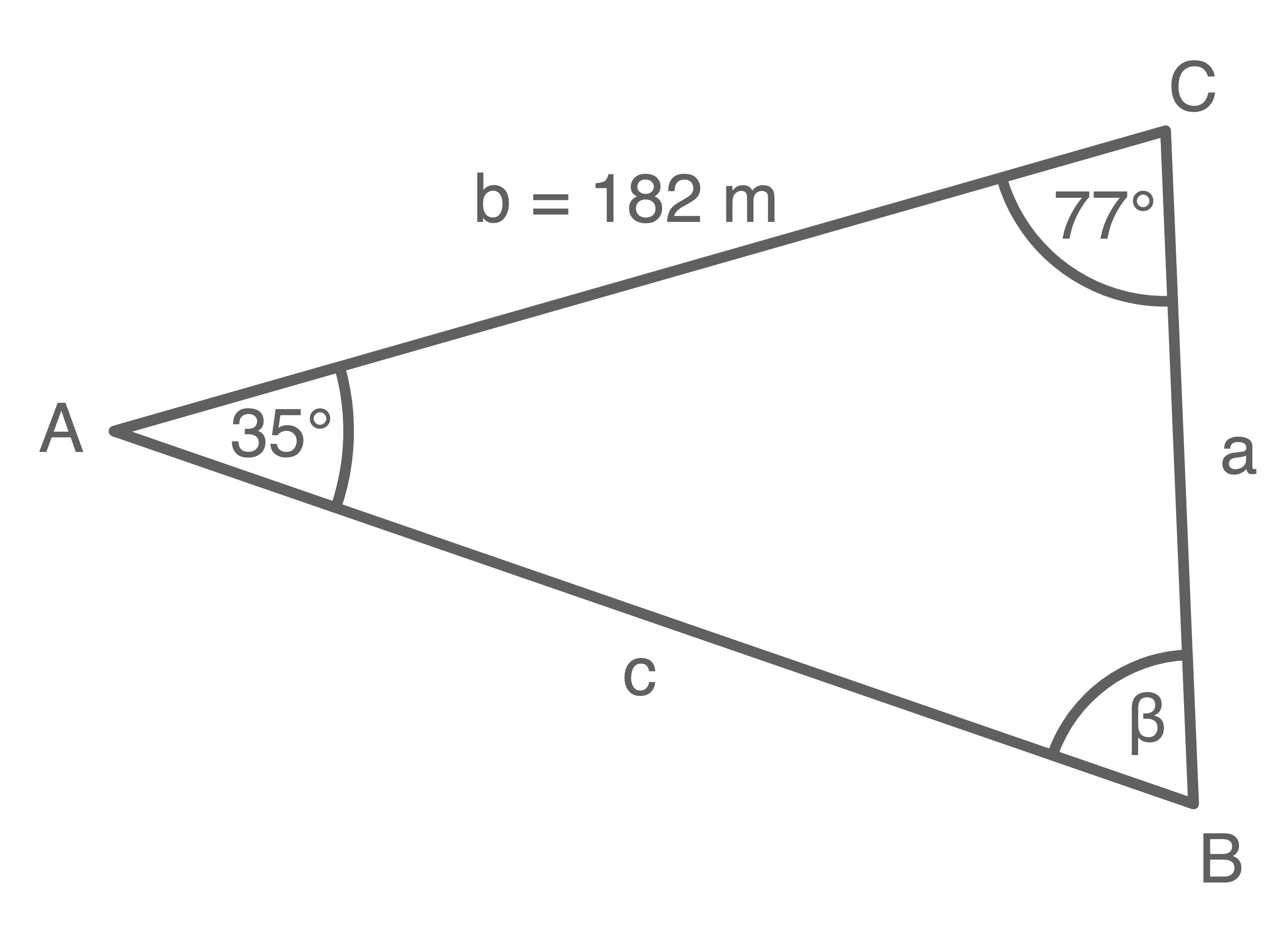 Mit dem Sinussatz folgt:
Mit dem Sinussatz folgt:
![\(\begin{array}[t]{rll}
\dfrac{c}{\sin\;\gamma}&=&\dfrac{b}{\sin\;\beta} \quad\scriptsize\mid\; \cdot \sin\;\gamma\\[5pt]
c&=&\dfrac{b}{\sin\;\beta}\cdot \sin\;\gamma\\[5pt]
c&=&\dfrac{182\,\text{m}}{\sin 68°}\cdot \sin 77°\\[5pt]
c&\approx& 191\,\text{m}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/3c235d8ed7ffcf0587436a5f7cfb3aa035513f81f2c2e496790432f077a4c58a?color=5a5a5a) Die Länge der Seite
Die Länge der Seite  beträgt ungefähr
beträgt ungefähr  .
.

b)
Zunächst muss der Mittelwert berechnet werden:
![\(\begin{array}[t]{rll}
M&=& \dfrac{190\,\text{m}+186\,\text{m}+192\,\text{m}+188\,\text{m}}{4}\\[5pt]
&=& 189 \,\text{m}
\end{array}\)](https://mathjax.schullv.de/5143f2ed3f88603f4d76f2e82533553ee464c416e5e62b13cc8e8d534c4d5a3e?color=5a5a5a) Die Abweichung ist dann:
Die Abweichung ist dann:
![\(\begin{array}[t]{rll}
A&=& 191\,\text{m}-189\,\text{m}\\[5pt]
&=& 2\,\text{m} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/58489f72ff219648b1bf110a91d390b9f3e3bcac2398a62510c637df9d902d30?color=5a5a5a) Die Abweichung beträgt
Die Abweichung beträgt  .
.
c)
Die Länge der Strecke  beträgt
beträgt  Im Maßstab
Im Maßstab  gilt:
gilt:
 Da die anliegenden Winkel der Strecke
Da die anliegenden Winkel der Strecke  bekannt sind, lässt sich das Dreieck nach dem Kongruenzsatz WSW eindeutig konstruieren.
bekannt sind, lässt sich das Dreieck nach dem Kongruenzsatz WSW eindeutig konstruieren.
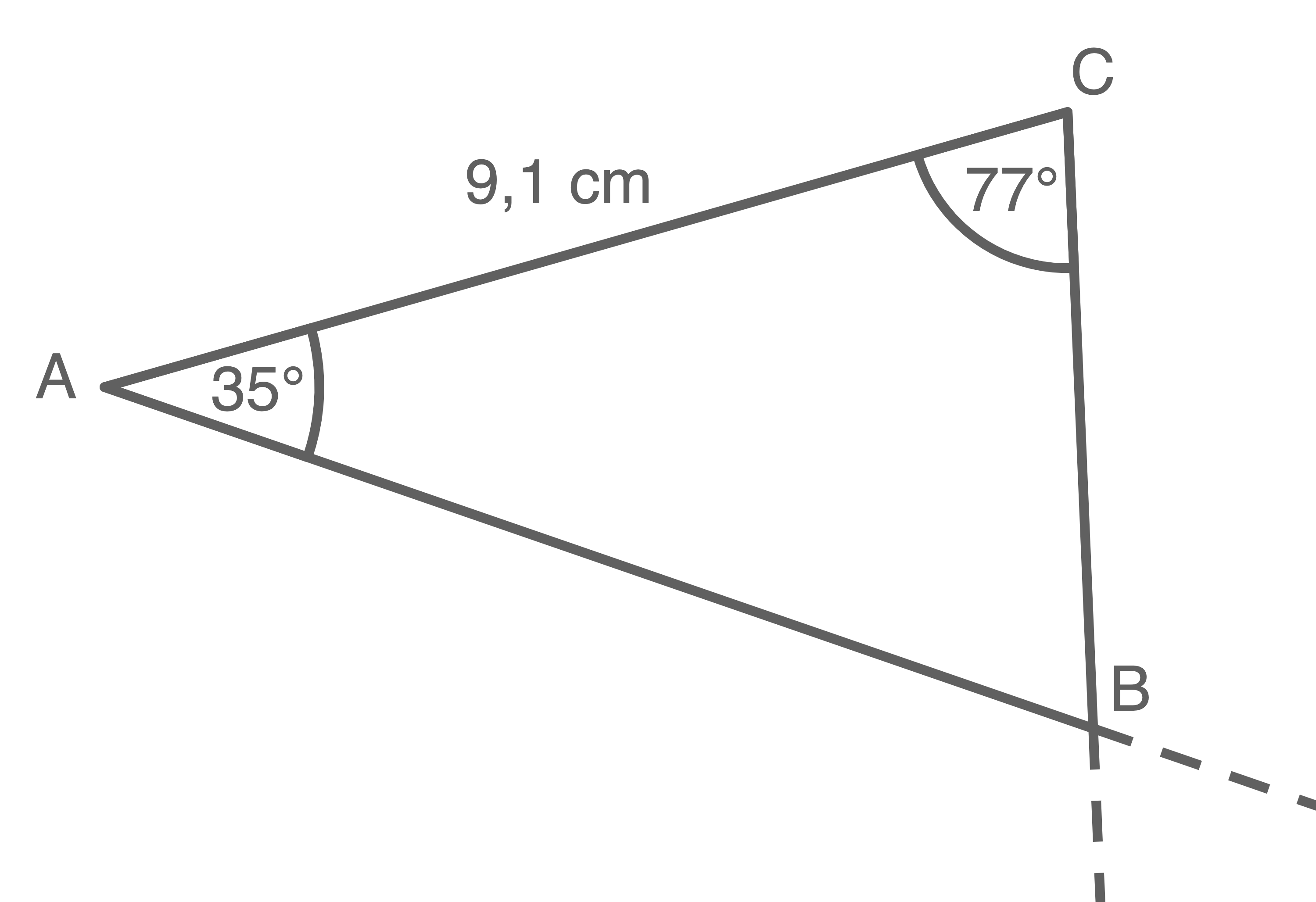 Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
