Verhalten an Polstellen
Definition
Eine Polstelle- Liegt im Nenner des Funktionsterms eine Nullstelle gerader Ordnung vor, so handelt es sich um eine Polstelle ohne Vorzeichenwechsel. Die Funktion divergiert dann links und rechts von der Definitionslücke jeweils gegen
oder
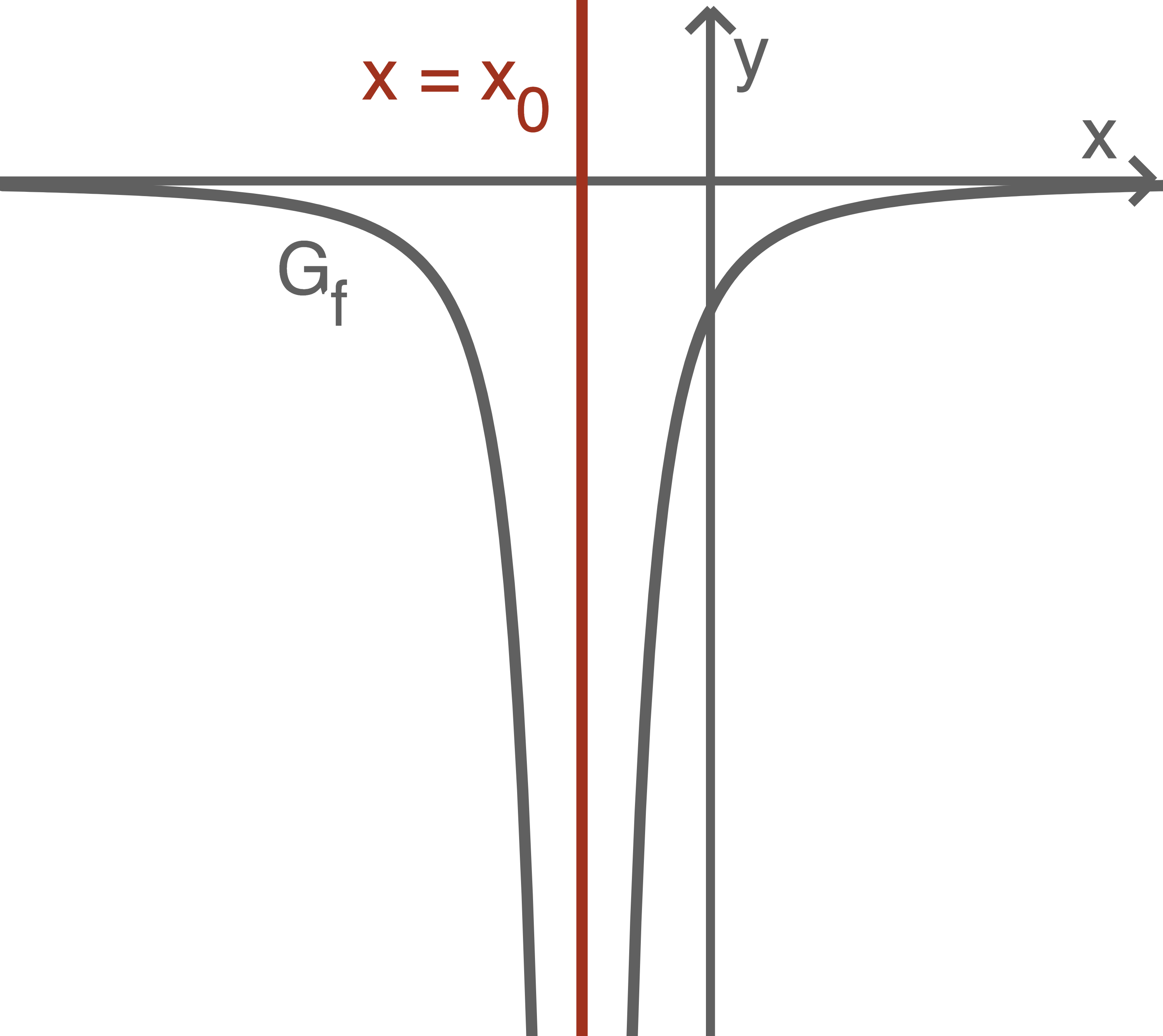
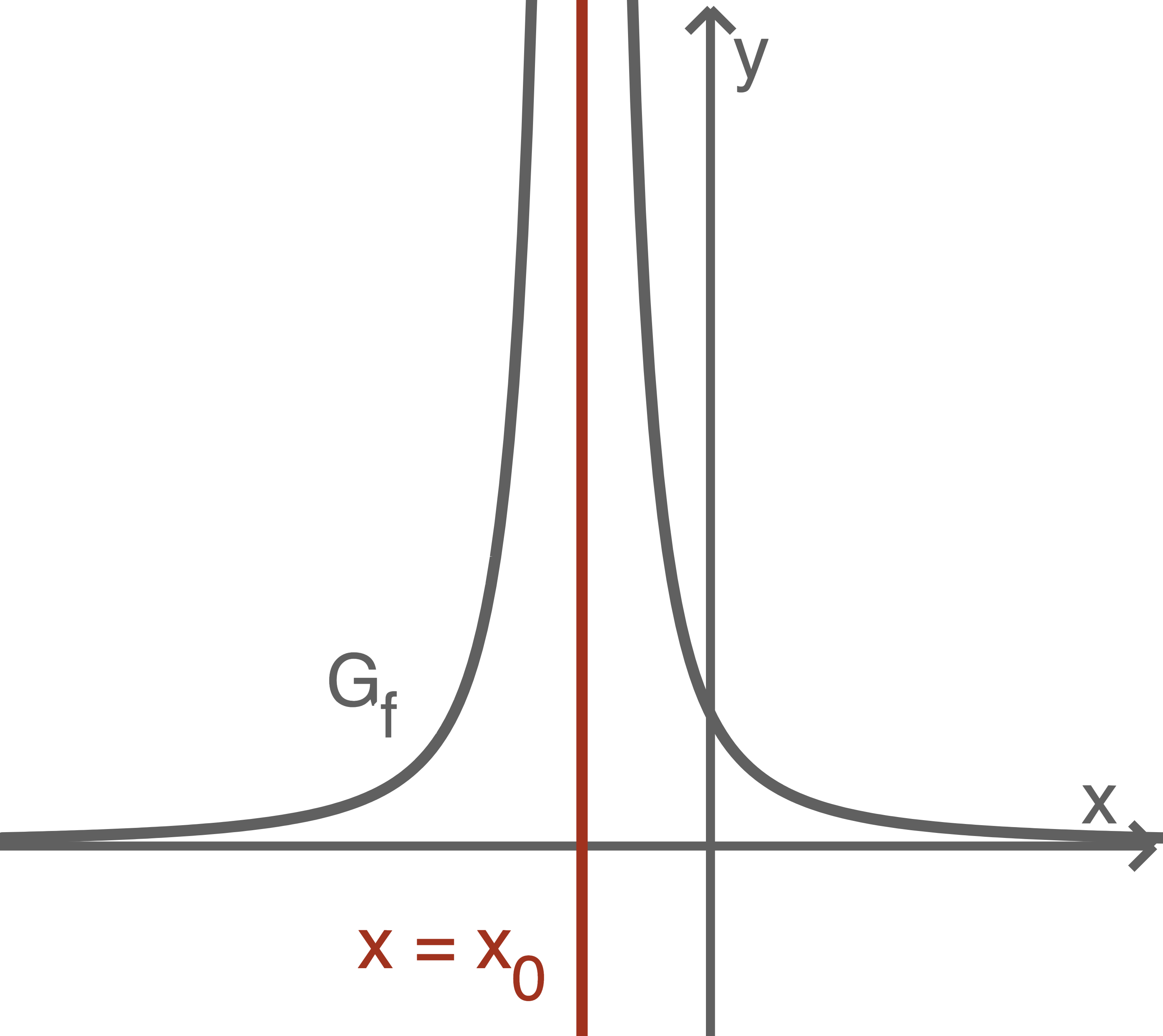
- Liegt im Nenner des Funktionsterms eine Nullstelle ungerader Ordnung vor, so handelt es sich um eine Polstelle mit Vorzeichenwechsel. Die Funktion divergiert dann links und rechts von der Definitionslücke entgegengesetzt.
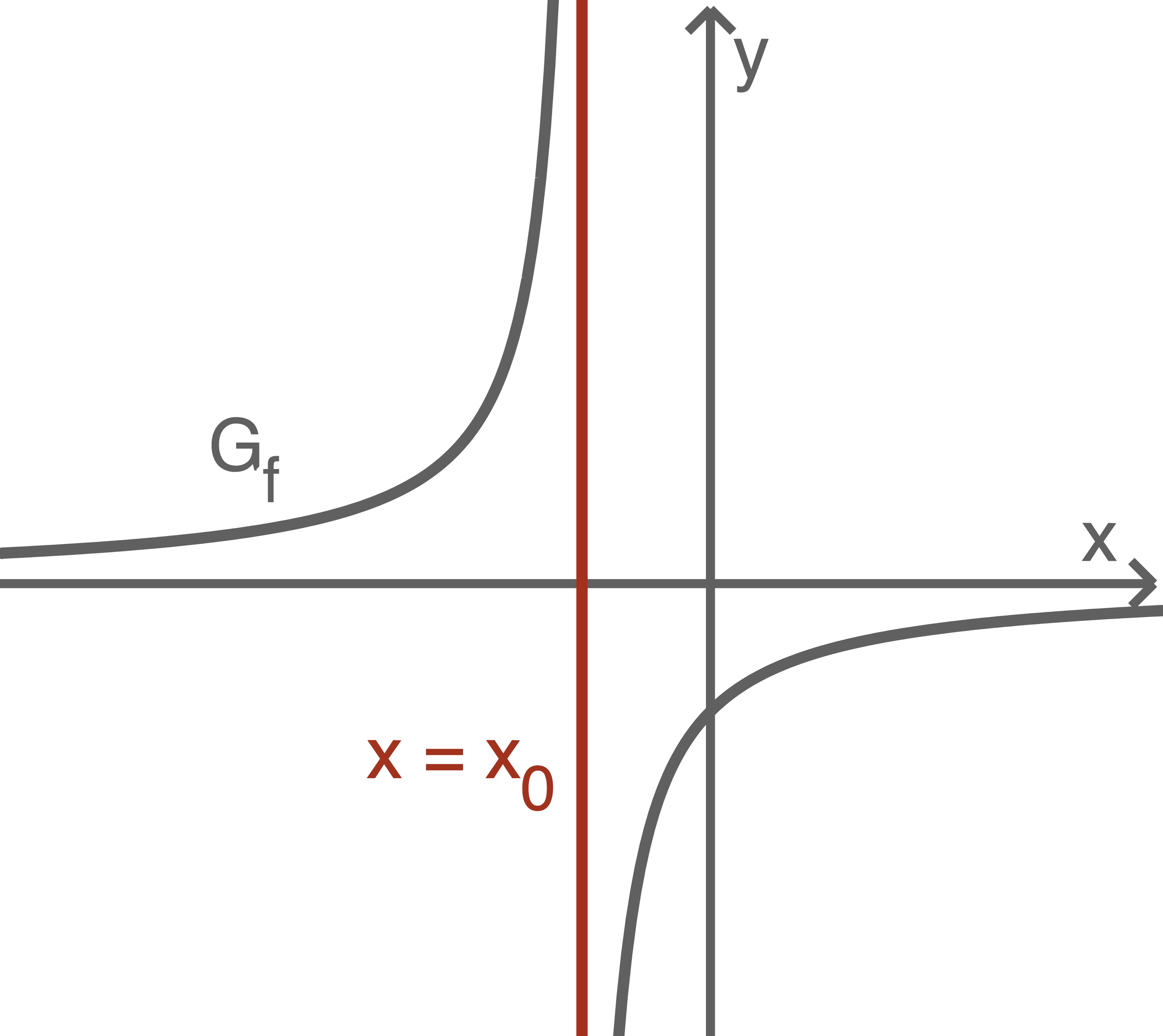
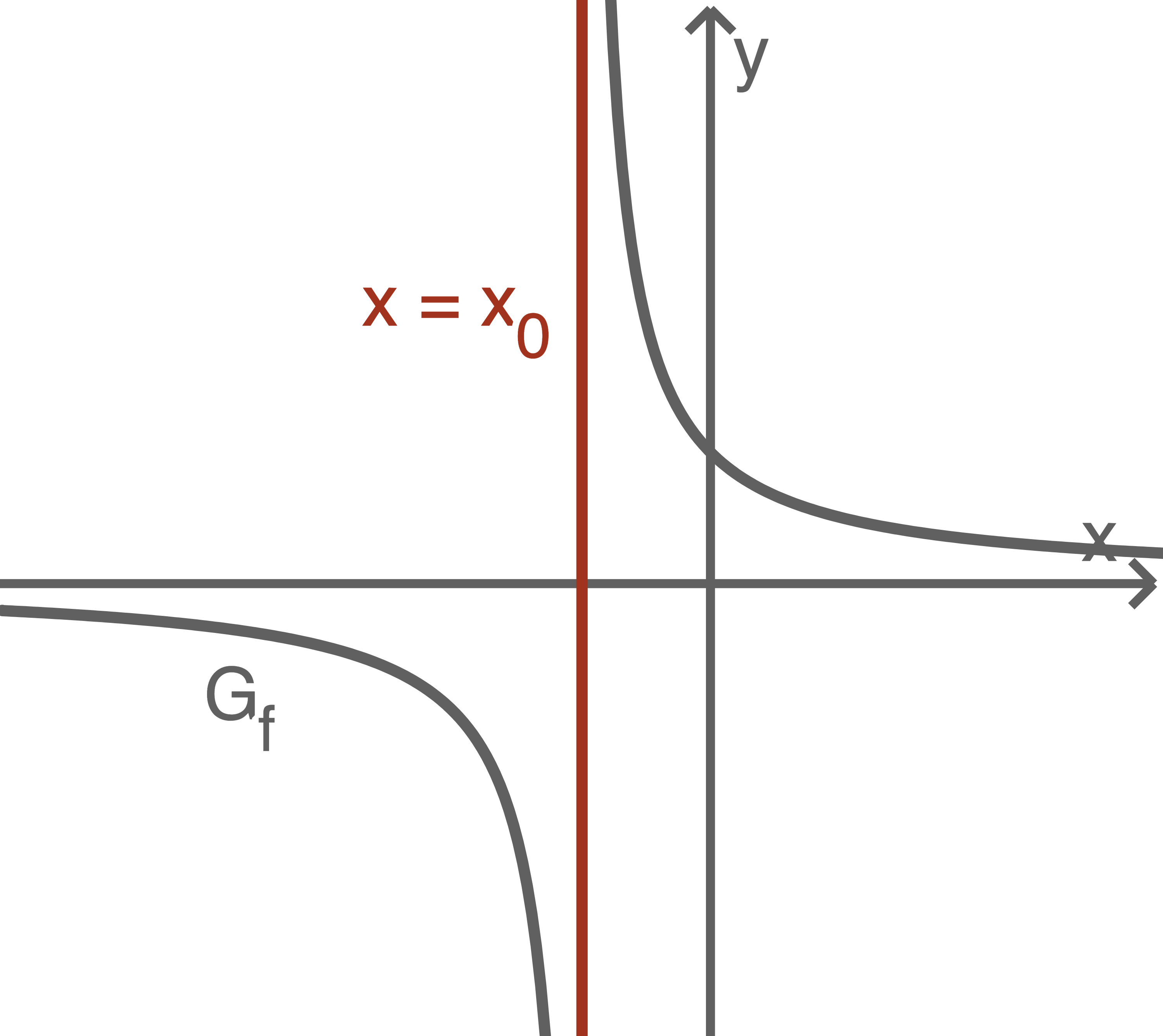
1
Gib alle Polstellen der Funktion  sowie ihre Art an.
sowie ihre Art an.






a)
b)
c)
d)
e)
f)
2
Gib eine gebrochen-rationale Funktion mit den angegebenen Eigenschaften an.
a)
Die Funktion  hat die Polstelle
hat die Polstelle  und es gilt
und es gilt  und
und 
b)
Die Funktion  hat die Polstelle
hat die Polstelle  ohne Vorzeichenwechsel und es gilt
ohne Vorzeichenwechsel und es gilt 
c)
Die Funktion  hat die Nullstelle
hat die Nullstelle  und die Polstellen
und die Polstellen  und
und  mit Vorzeichenwechsel, wobei
mit Vorzeichenwechsel, wobei  gilt.
gilt.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Polstelle  mit Vorzeichenwechsel
mit Vorzeichenwechsel
b)
c)
Polstelle  ohne Vorzeichenwechsel
ohne Vorzeichenwechsel
d)
e)
Polstelle  ohne Vorzeichenwechsel
ohne Vorzeichenwechsel
f)
Polstellen  und
und  mit Vorzeichenwechsel
mit Vorzeichenwechsel
2
a)
b)
c)