Extremstellen, Extremwerte und Extrempunkte
Definition
Der Funktionswert  einer Funktion
einer Funktion  mit maximaler Definitionsmenge
mit maximaler Definitionsmenge  und
und  heißt lokales Maximum von
heißt lokales Maximum von  wenn eine Umgebung
wenn eine Umgebung  existiert, sodass gilt:
existiert, sodass gilt:
 für alle
für alle  mit
mit 
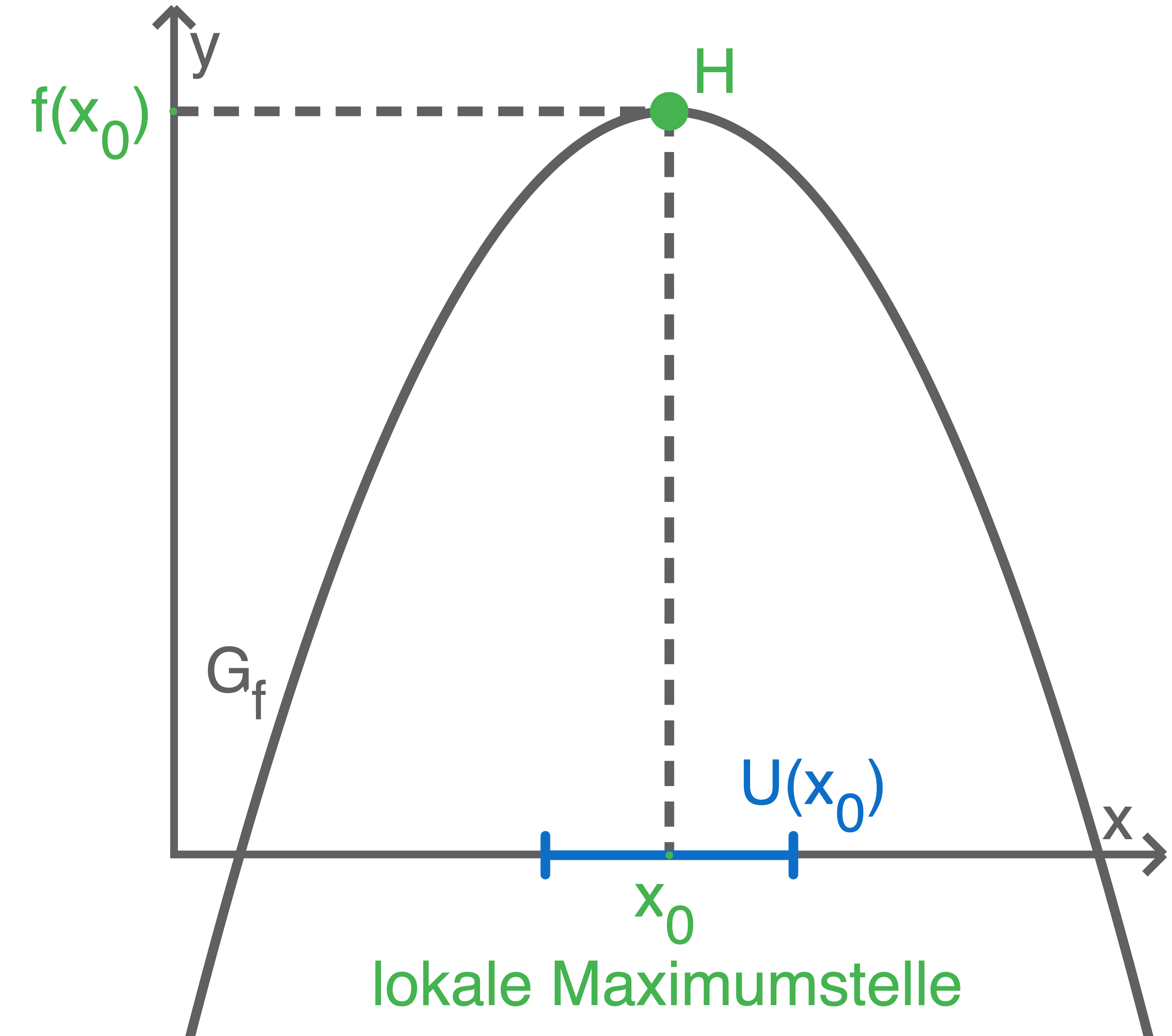 Der Punkt
Der Punkt  heißt Hochpunkt des Graphen von
heißt Hochpunkt des Graphen von 

Der Funktionswert  einer Funktion
einer Funktion  mit maximaler Definitionsmenge
mit maximaler Definitionsmenge  und
und  heißt lokales Minimum von
heißt lokales Minimum von  wenn eine Umgebung
wenn eine Umgebung  existiert, sodass gilt:
existiert, sodass gilt:
 für alle
für alle  mit
mit 
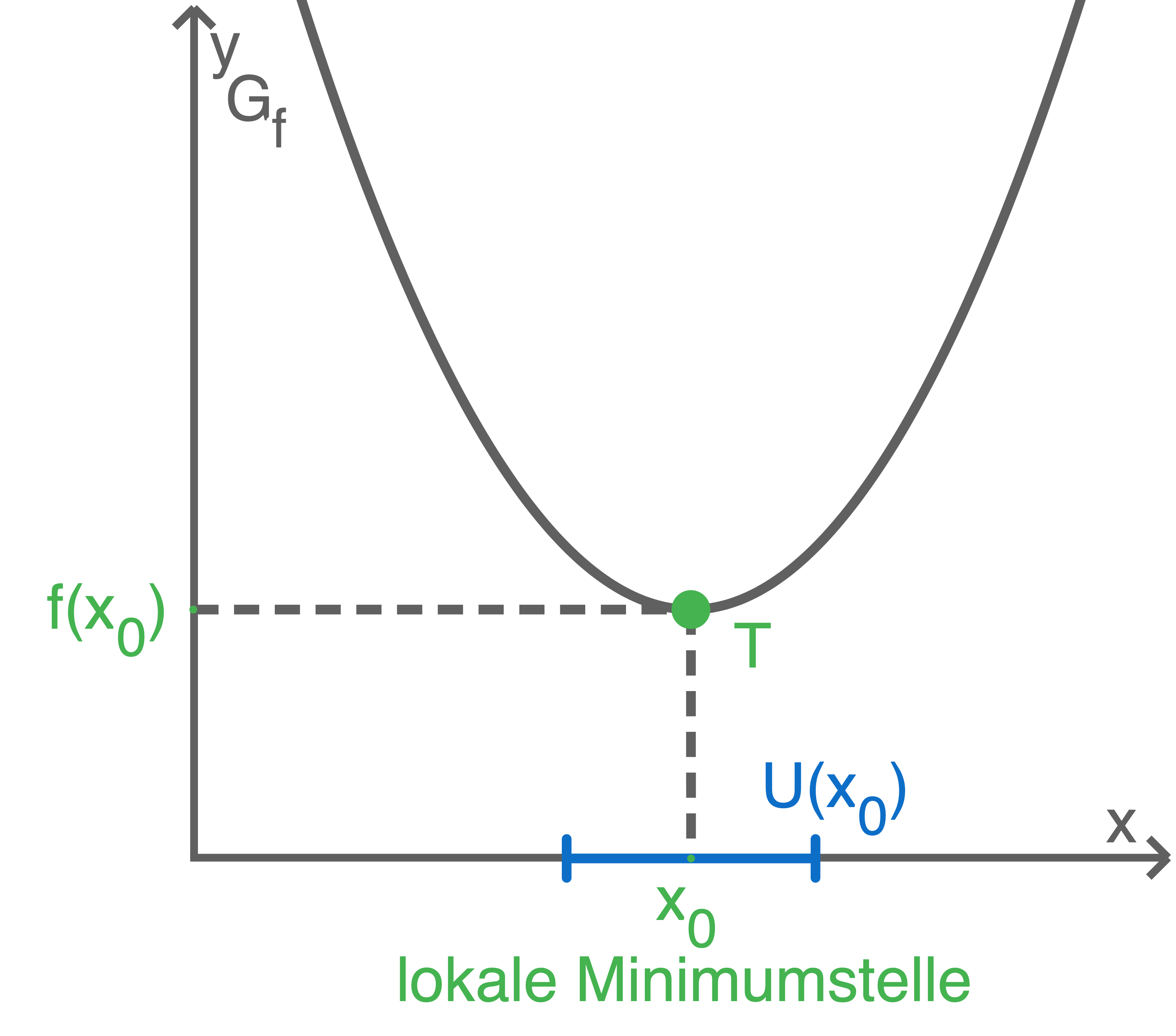 Der Punkt
Der Punkt  heißt Tiefpunkt des Graphen von
heißt Tiefpunkt des Graphen von 
Hoch- und Tiefpunkte werden auch Extrempunkte genannt. Eine Stelle 
Satz
In einem Intervall
1
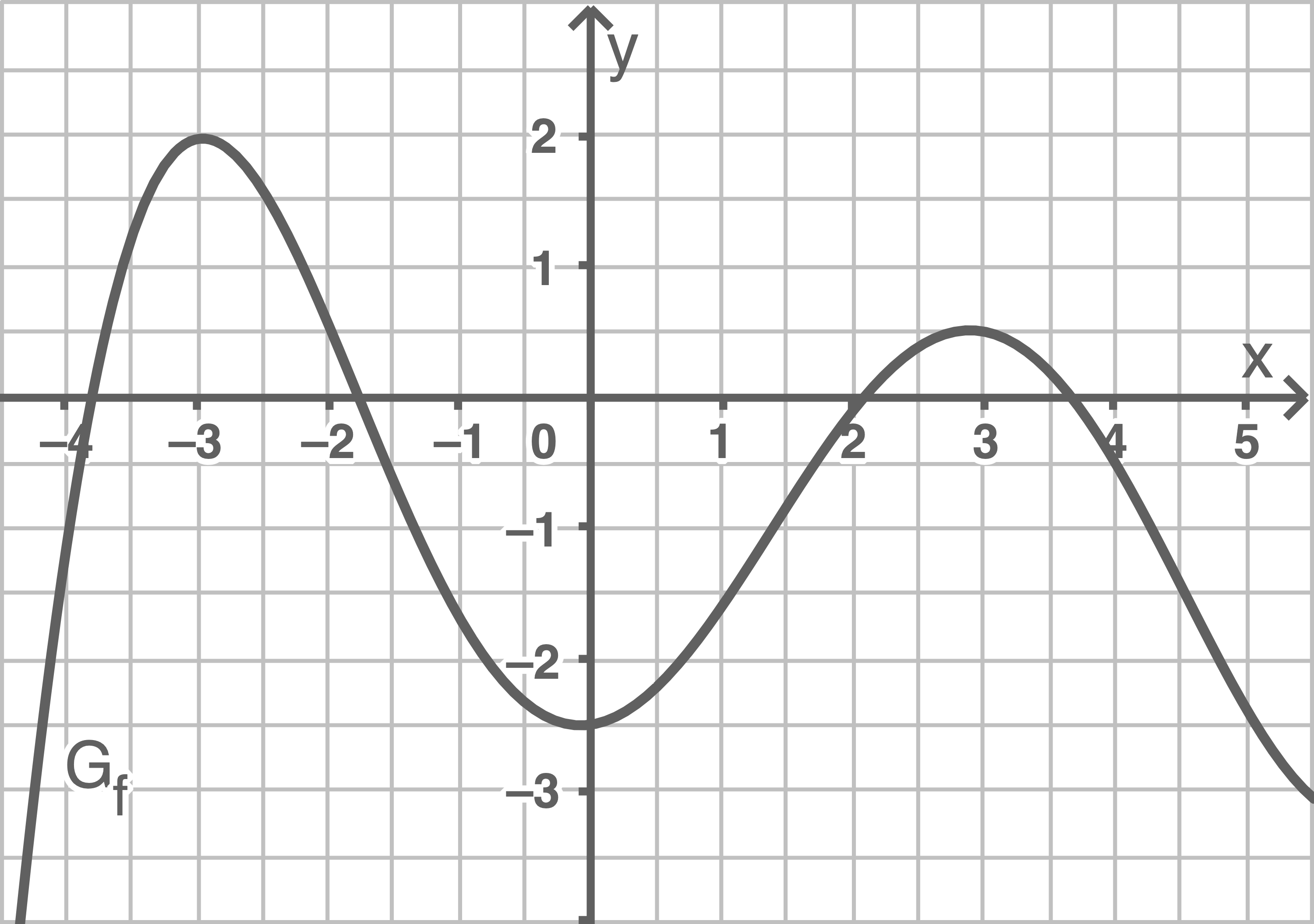
Die Abbildung zeigt den Graphen  der Funktion
der Funktion 
a)
Lies die Koordinaten der Hoch- und Tiefpunkte ab.
b)
Gib an, ob im Intervall ![\(I=[-4;5]\)](https://mathjax.schullv.de/603640661e4c1b11b00137191c7df1fc01f2f9a6c9db90e79554a4f09737762d?color=5a5a5a) jeweils ein lokales oder ein globales Extremum vorliegt.
jeweils ein lokales oder ein globales Extremum vorliegt.
2
Berechne die Stellen der Funktion  an denen ein Extremum vorliegen könnte.
an denen ein Extremum vorliegen könnte.



a)
b)
c)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Hochpunkte:  Tiefpunkt:
Tiefpunkt: 
b)
Im angegebenen Intervall ist  ein globales und
ein globales und  ein lokales Maximum.
Der Tiefpunkt
ein lokales Maximum.
Der Tiefpunkt  ist ein globaler Tiefpunkt, da auch die Werte an den Rändern des Intervalls nicht kleiner als der Extremwert von
ist ein globaler Tiefpunkt, da auch die Werte an den Rändern des Intervalls nicht kleiner als der Extremwert von  sind.
sind.
2
a)
b)
c)