Kriterien für Extremstellen

Vorzeichenwechsel

Die Funktion $f$ sei im Intervall $I=]a;b[$ mit innerer Stelle $x_0$ differenzierbar.

Gilt $\(f$ und hat $\(f$ an der Stelle $x_0$ einen Vorzeichenwechsel von + nach -, so hat $f$ bei $x_0$ ein lokales Maximum.

Gilt $\(f$ und hat $\(f$ an der Stelle $x_0$ einen Vorzeichenwechsel von - nach +, so hat $f$ bei $x_0$ ein lokales Minimum.

Die Bedingung $\(f$ ist eine notwendige Bedingung für das Vorliegen einer Extremstelle. Das bedeutet, dass die Bedingung stets erfüllt ist, wenn eine Extremstelle vorliegt.

Es ist jedoch keine hinreichende Bedingung, die eine Extremstelle garantiert. An einem sogenannten Terassenpunkt oder auch Sattelpunkt gilt $\(f$ aber das Monotonieverhalten der Funktion ändert sich nicht.

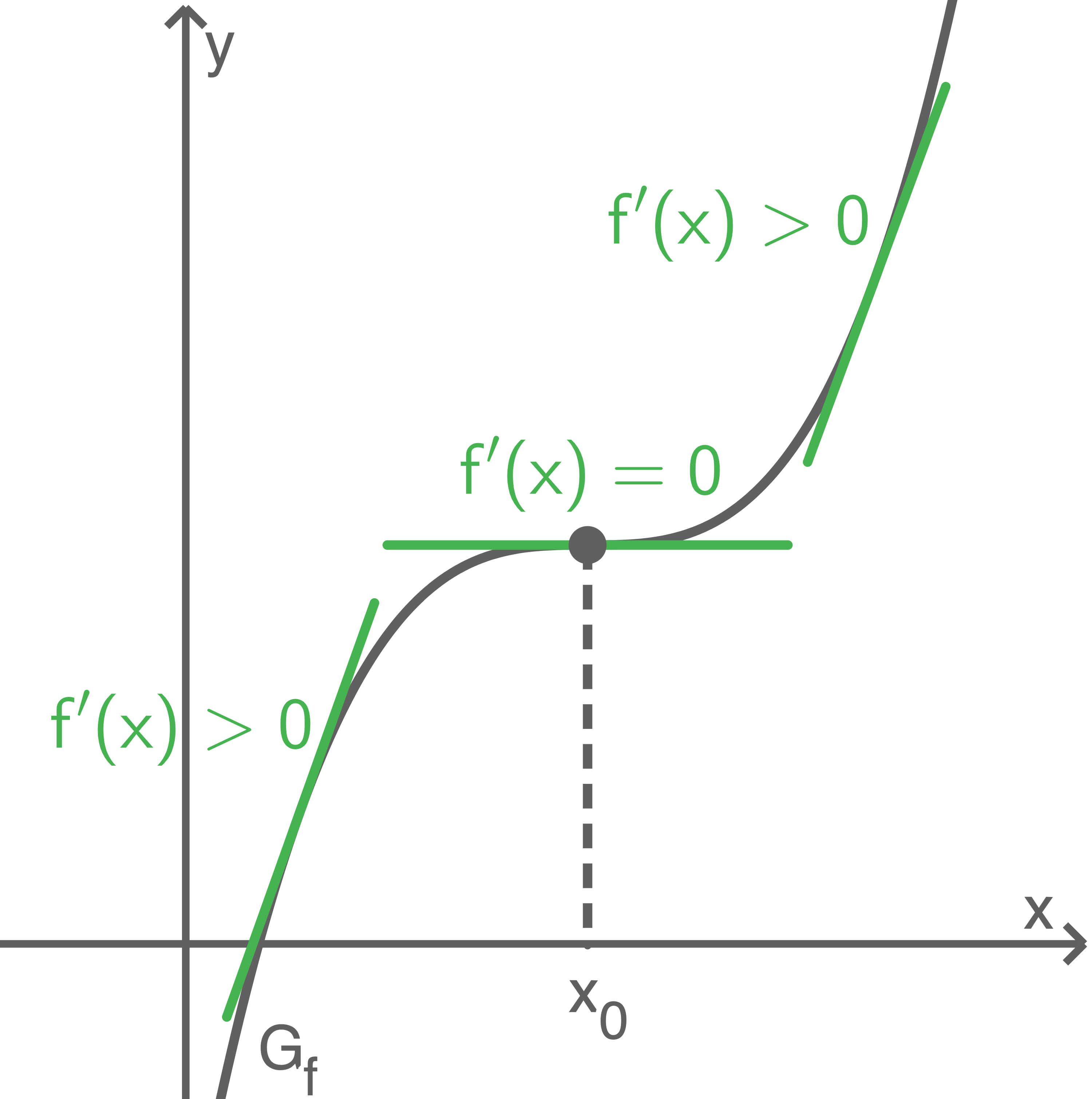
extremstellen, extremwerte, extrempunkte, terassenpunkt, sattelpunkt, notwendiges kriterium, hinreichendes kriterium

Zweite Ableitung

Die Funktion $f$ sei im Intervall $I=]a;b[$ mit innerer Stelle $x_0\in I$ zweimal differenzierbar.

Gilt $\(\boldsymbol{f$ und $\(\boldsymbol{f$ dann hat $f$ an der Stelle $x_0$ ein lokales Maximum.

Gilt $\(\boldsymbol{f$ und $\(\boldsymbol{f$ dann hat $f$ an der Stelle $x_0$ ein lokales Minimum.

Die Bedingung $\(f$ und $\(f$ ist eine hinreichende Bedingung für eine Extremstelle. Sie ist jedoch nicht notwendig. Beispielsweise für die Funktion $f$ mit $f(x)=x^4$ gilt $\(f$ aber $\(f$ hat bei $x=0$ einen Vorzeichenwechsel und somit ein lokales Extremum.

$f(x)=x^2-5x+3$

$\(f$

Notwendiges Kriterium

$\(\begin{array}[t]{rll} f$

Vorzeichenwechsel

Für $x\lt 2,5$ gilt $\(f$

Für $x\gt 2,5$ gilt $\(f$

$f(2,5)=2,5^2-5\cdot 2,5+3=-4,25$

Der Graph von $f$ hat den Tiefpunkt $T(2,5\mid -4,25).$

$f(x)=\dfrac{1}{4}x^3$ in $I=[-2;2]$

$\(f$

Notwendiges Kriterium

$\(\begin{array}[t]{rll} f$

Vorzeichenwechsel

Für $x\lt 0$ gilt $\(f$

Für $x\gt 0$ gilt $\(f$

An der Stelle $x=0$ hat $f$ kein Extremum, sondern einen Sattelpunkt.

Randextrema

Da der Graph von $f$ monoton steigt, sind der höchste und der niedrigste Wert durch die Randextrema gegeben.

$f(-2)=\dfrac{1}{4}\cdot (-2)^3=-2$

$f(2)=\dfrac{1}{4}\cdot 2^3=2$

In den Intervallrändern besitzt $f$ jeweils ein Randextremum:

Für $x=-2$ nimmt $f$ das globale Minimum an.

Für $x=2$ nimmt $f$ das globale Maximum an.

$f(x)=x^3-2x^2+1$

$\(f$

Notwendiges Kriterium

$\(\begin{array}[t]{rll} f$

Vorzeichenwechsel

Für $x\lt 0$ gilt $\(f$

Für $0\lt x\lt \dfrac{4}{3}$ gilt $\(f$

Für $x\gt \dfrac{4}{3}$ gilt $\(f$

$f(0)=0^3-2\cdot 0^2+1=1$

$f\left(\dfrac{4}{3}\right)=\left(\dfrac{4}{3}\right)^3-2\cdot \left(\dfrac{4}{3}\right)^2+1=-\dfrac{5}{27}$

Der Graph von $f$ hat den Hochpunkt $H(0\mid 1)$ und den Tiefpunkt $T\left(\dfrac{4}{3}\,\bigg \vert \,-\dfrac{5}{27}\right).$

$f(x)=-x^3+2x^2+2$

$\(f$

Notwendiges Kriterium

$\(\begin{array}[t]{rll} f$

Hinreichendes Kriterium

$\(f$

Bei $x=0$ liegt ein Tiefpunkt vor.

$\(f$

Bei $x=\dfrac{4}{3}$ liegt ein Hochpunkt vor.

$f(0)=-0^3+2\cdot 0^2+2=2$

Der Hochpunkt hat die Koordinaten $H(0\mid 2).$

$f\left(\dfrac{4}{3}\right)=-\left(\dfrac{4}{3}\right)^3+2\cdot \left(\dfrac{4}{3}\right)^2+2=\dfrac{86}{27}$

Der Tiefpunkt hat die Koordinaten $T\left(\dfrac{4}{3}\,\bigg \vert \, \dfrac{86}{27}\right).$

$f(x)=x^4+2x^3$

$\(f$

Notwendiges Kriterium

$\(\begin{array}[t]{rll} f$

Hinreichendes Kriterium

$\(f$

Mit der zweiten Ableitung kann nicht festgestellt werden, ob ein Hochpunkt oder ein Tiefpunkt vorliegt. Mit dem Vorzeichenwechselkriterium folgt:

Für $-1,5\lt x \lt 0$ gilt $\(f$

Für $x\gt 0$ gilt $\(f$

An der Stelle $x=0$ liegt also kein Extremum, sondern ein Sattelpunkt vor.

$\(f$

Bei $x=-1,5$ liegt ein Tiefpunkt vor.

$f(-1,5)=(-1,5)^4+2\cdot (-1,5)^3\approx -1,7$

Der Tiefpunkt hat die Koordinaten $T(-1,5\mid -1,7).$

$f(x)=\dfrac{1}{3}x^3-x$

$\(f$

Notwendiges Kriterium

$\(\begin{array}[t]{rll} f$

Hinreichendes Kriterium

$\(f$

Bei $x=1$ liegt ein Tiefpunkt vor.

$\(f$

Bei $x=-1$ liegt ein Hochpunkt vor.

$f(1)=\dfrac{1}{3}\cdot 1^3-1=-\dfrac{2}{3}$

Der Tiefpunkt hat die Koordinaten $T\left(1\,\bigg \vert \,-\dfrac{2}{3}\right).$

$f(-1)=\dfrac{1}{3}\cdot (-1)^3-(-1)=\dfrac{2}{3}$

Der Hochpunkt hat die Koordinaten $H\left(-1\,\bigg \vert \,\dfrac{2}{3}\right).$

$f(x)=x^4-3$

$\(f$

Notwendiges Kriterium

$\(\begin{array}[t]{rll} f$

Hinreichendes Kriterium

$\(f$

Mit der zweiten Ableitung kann nicht festgestellt werden, ob ein Hochpunkt oder ein Tiefpunkt vorliegt. Mit dem Vorzeichenwechselkriterium folgt:

Für $x\lt 0$ gilt $\(f$

Für $x\gt 0$ gilt $\(f$

An der Stelle $x=0$ liegt also ein Tiefpunkt vor.

$f(0)=0^4-3=-3$

Der Tiefpunkt hat die Koordinaten $T(0\mid -3).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?