Schnittpunkte von Graphen ermitteln
Um die Koordinaten der Schnittpunkte zweier Funktionsgraphen 
und 
zu bestimmen, folgt man diesem Vorgehen:
und 
berechnen.
1. Funktionsterme gleichsetzen und Gleichung lösen
![\(\begin{array}[t]{rll}
\dfrac{3}{x+4}&=& \dfrac{3}{(x-2)^2} \quad \scriptsize \mid\; \cdot (x+4)\cdot (x-2)^2 \\[5pt]
3(x-2)^2&=& 3(x+4) \quad \scriptsize \mid\; :3 \\[5pt]
(x-2)^2&=& x+4 \\[5pt]
x^2-4x+4&=& x+4 \quad \scriptsize \mid\; -4 \\[5pt]
x^2-4x&=& x \quad \scriptsize \mid\; -x \\[5pt]
x^2-5x&=& 0 \\[5pt]
x(x-5)&=& 0 \\[5pt]
x_1&=& 0 \\[5pt]
x_2&=& 5
\end{array}\)](https://mathjax.schullv.de/4f78faa08c2ce4e4a1bc75031950e6d477ae46c0035c2261c9f89c39d75e6c9d?color=5a5a5a)
2. 
-Werte berechnen
Schnittpunkte von und 
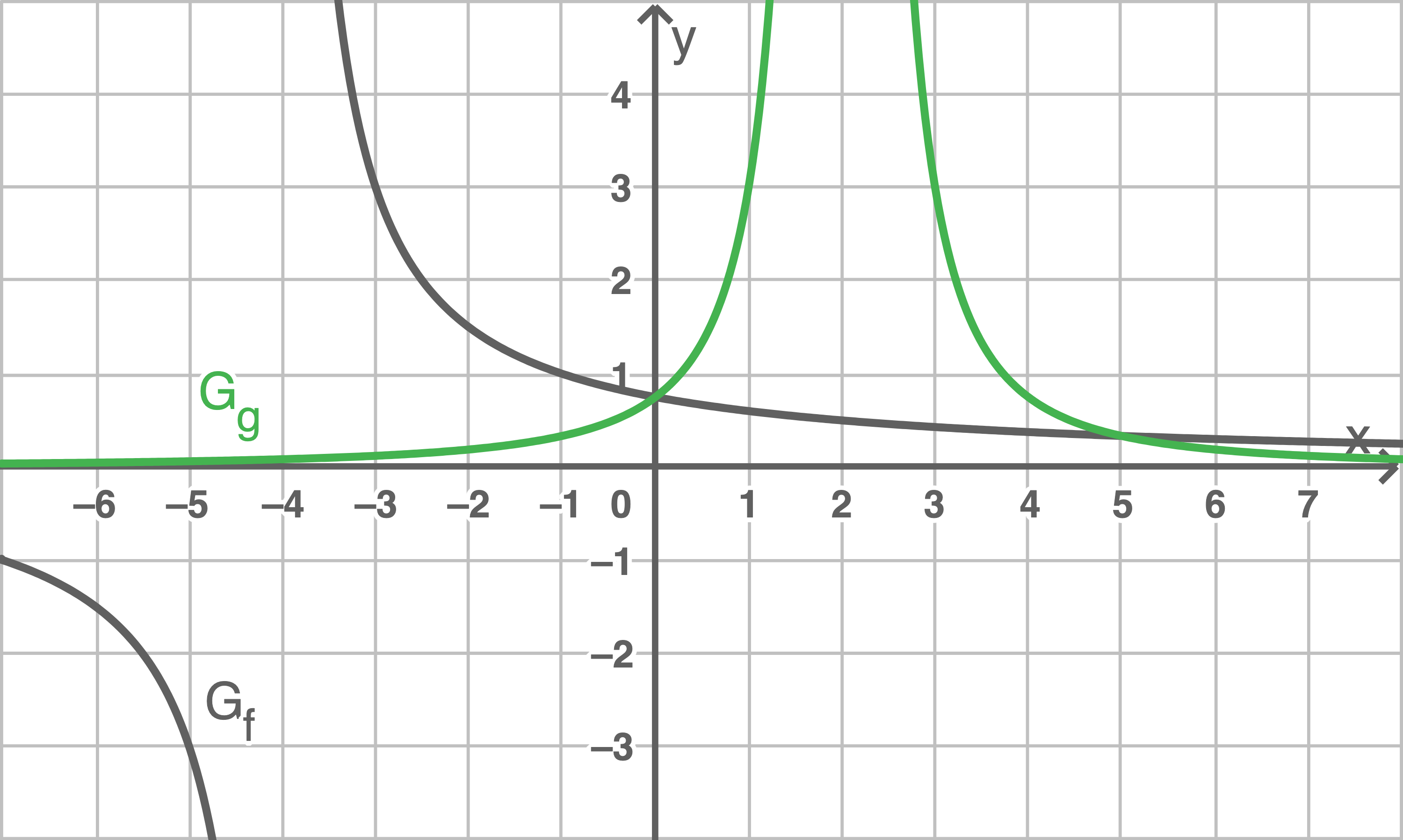
- Funktionsterme gleichsetzen und Gleichung lösen:
-Koordinate berechnen:
-Koordinate eines Schnittpunkts in einen der beiden Funktionsterme einsetzen
Beispiel
Schnittpunkte der Funktionen
1
Löse die Gleichung.
a)
b)
c)
d)
2
Berechne die Koordinaten der Schnittpunkte der Funktionsgraphen und 
a)
b)
c)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
d)
2
a)
1. Funktionsterme gleichsetzen und Gleichung lösen
![\(\begin{array}[t]{rll}
\dfrac{4}{x-2}&=& \dfrac{x}{x+4} \quad \scriptsize \mid\;\cdot (x-2)\cdot (x+4) \\[5pt]
4(x+4)&=& x\cdot (x-2) \\[5pt]
4x+16&=& x^2-2x \quad \scriptsize \mid\; -x^2+2x \\[5pt]
-x^2+6x+16&=& 0
\end{array}\)](https://mathjax.schullv.de/20b43dee34304481d89874c57c9e79b8ebdbd1181649ed7fb8b4c5ffe50e4bc0?color=5a5a5a)
Mit der 
-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1/2}&=& \dfrac{-6\pm\sqrt{6^2-4\cdot (-1)\cdot 16}}{2\cdot (-1)} \\[5pt]
&=& \dfrac{-6\pm\sqrt{100}}{-2} \\[5pt]
x_1&=& -2 \\[5pt]
x_2&=& 8
\end{array}\)](https://mathjax.schullv.de/00eccb5cfed986b80ca59104b10457e14a48130766ebfe619c15d6b84d804a91?color=5a5a5a)
2. -Koordinaten berechnen
Schnittpunkte von und
b)
1. Funktionsterme gleichsetzen und Gleichung lösen
![\(\begin{array}[t]{rll}
\dfrac{1}{x-2}&=& \dfrac{1}{x-3} \quad \scriptsize \mid\;\cdot (x-2)\cdot (x-3) \\[5pt]
x-3&=& x-2 \quad \scriptsize \mid\;-x \\[5pt]
-3&=& -2
\end{array}\)](https://mathjax.schullv.de/6bd77f6a81b69f3e2f48eb0823d2c210a072c56de714cb99251b9083ea4214bd?color=5a5a5a)
Die Aussage ist falsch. Die Graphen haben keinen Schnittpunkt.
c)
1. Funktionsterme gleichsetzen und Gleichung lösen
![\(\begin{array}[t]{rll}
\dfrac{4}{x-2}&=& \dfrac{x-2}{10-x} \quad \scriptsize \mid\; \cdot (x-2)\cdot (10-x) \\[5pt]
4\cdot (10-x)&=& (x-2)(x-2) \\[5pt]
40-4x&=& x^2-4x+4 \quad \scriptsize \mid\; +4x \\[5pt]
40&=& x^2+4 \quad \scriptsize \mid\; -4 \\[5pt]
36&=& x^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
x_1&=& 6 \\[5pt]
x_2&=& -6
\end{array}\)](https://mathjax.schullv.de/b6d900e37750b320245eea68cd72f56c22fab27f8c95d2069aff1ea01f3ba5fc?color=5a5a5a)
2. -Koordinaten berechnen
Schnittpunkte von und
