Stetigkeit
Definition
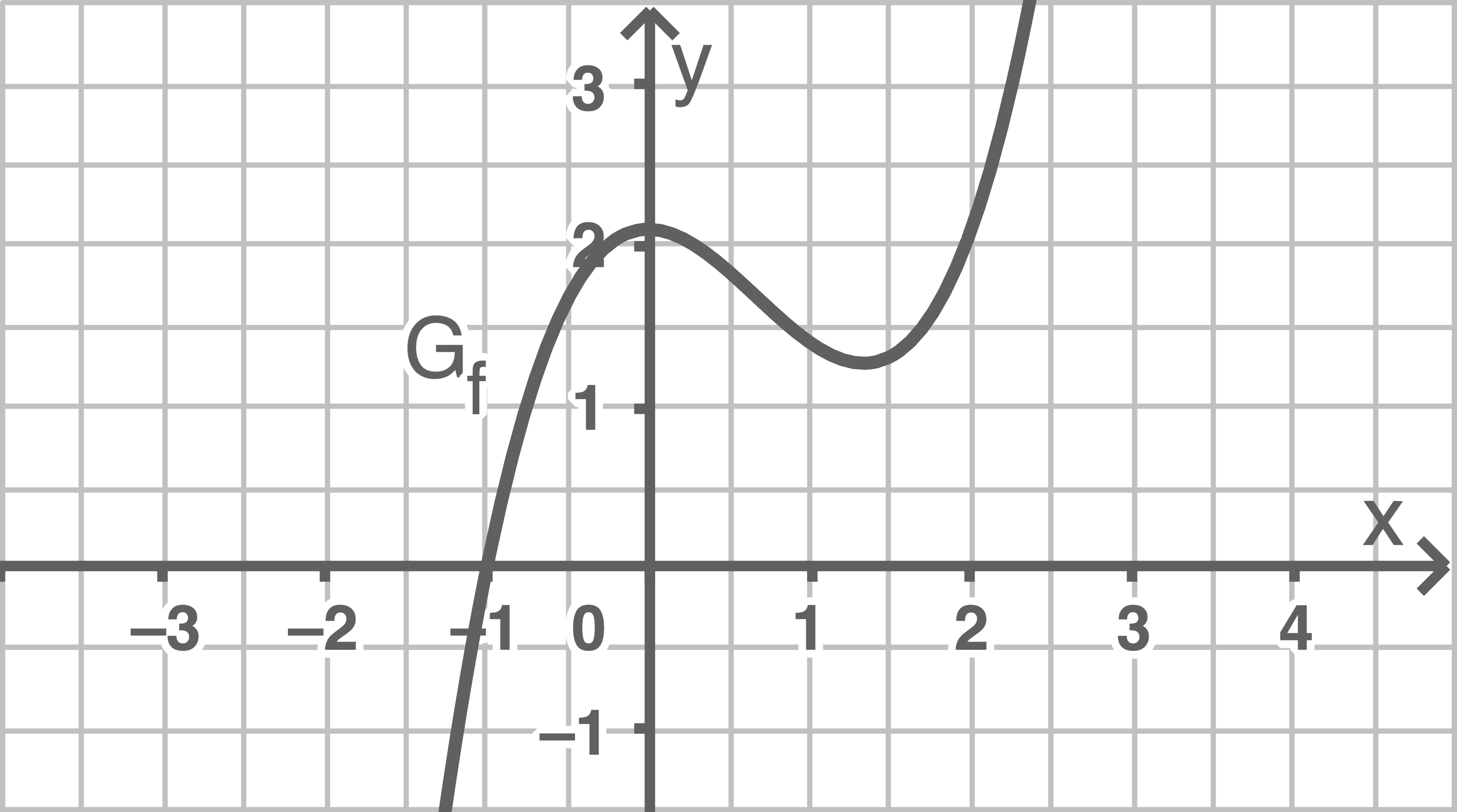
Eine Funktion  heißt auf einem Intervall stetig, wenn sie auf diesem Intervall definiert ist und ihr Graph dort ohne Absetzen gezeichnet werden kann.
heißt auf einem Intervall stetig, wenn sie auf diesem Intervall definiert ist und ihr Graph dort ohne Absetzen gezeichnet werden kann.
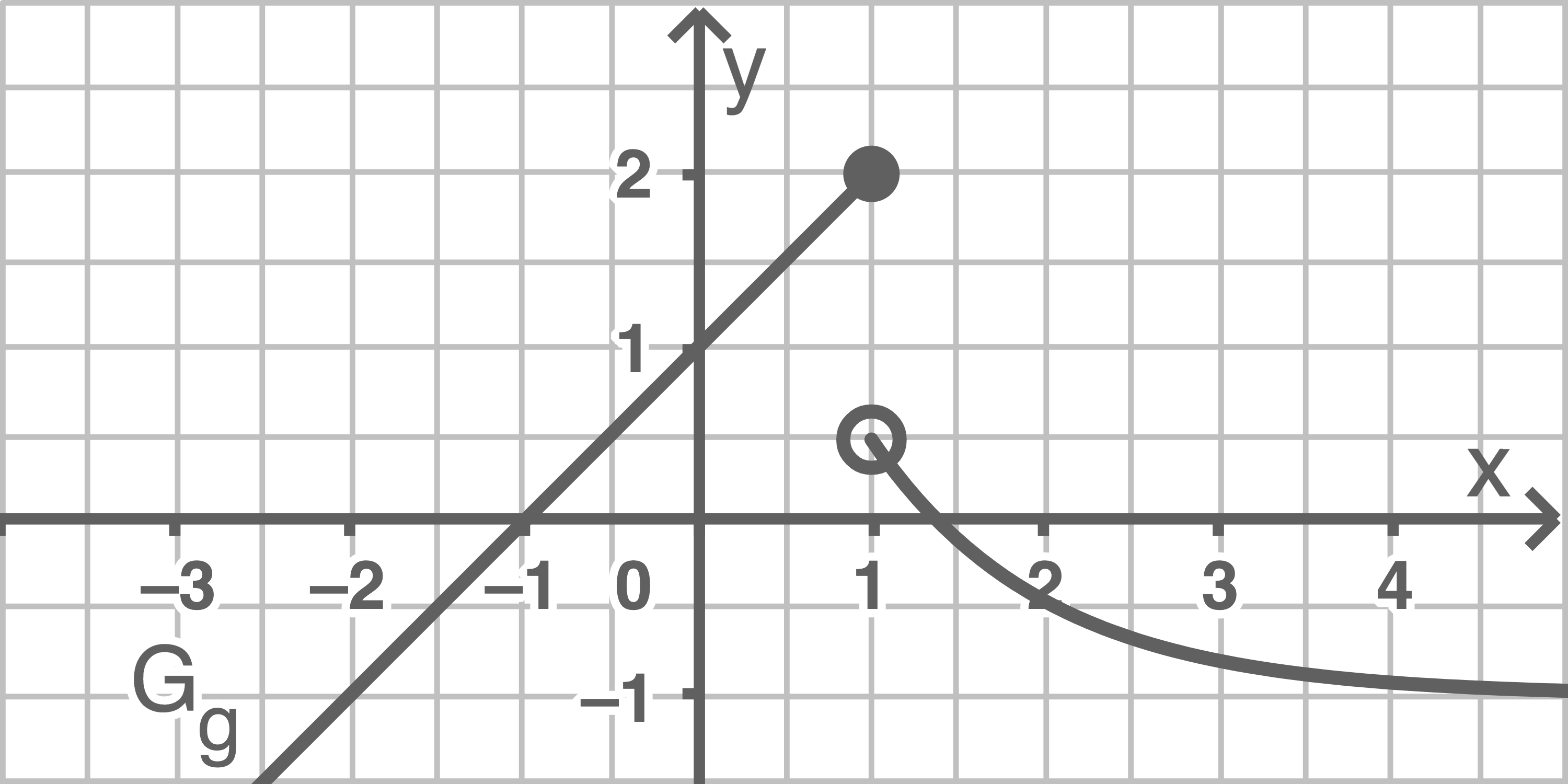
Eine Funktion  heißt an einer Stelle der Definitionsmenge unstetig, wenn ihr Graph an dieser Stelle einen Sprung macht, also eine sogenannte Sprungstelle hat.
heißt an einer Stelle der Definitionsmenge unstetig, wenn ihr Graph an dieser Stelle einen Sprung macht, also eine sogenannte Sprungstelle hat.


Beispiel
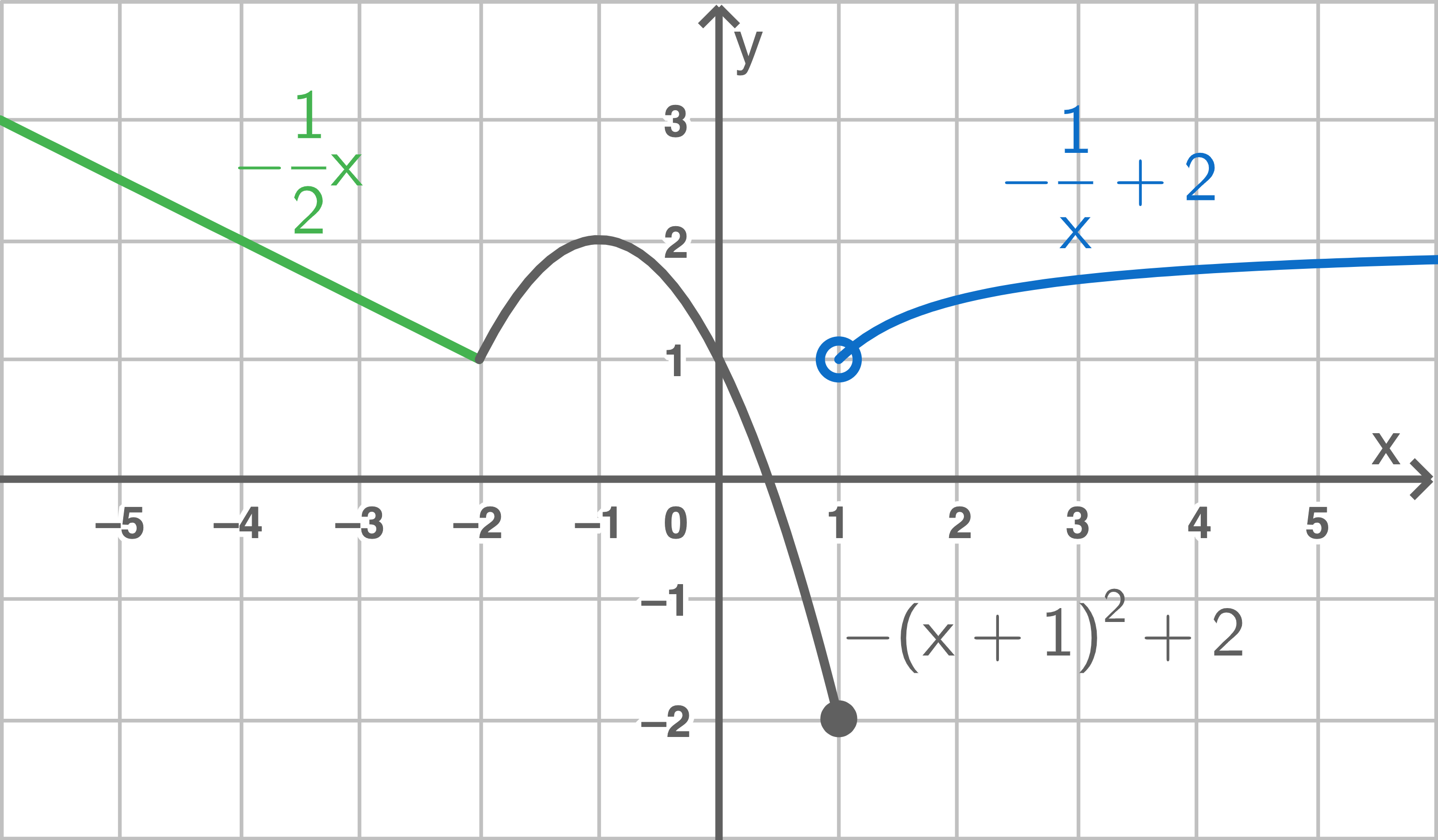
Die Funktion  ist abschnittsweise wie folgt definiert:
ist abschnittsweise wie folgt definiert:

1
Skizziere den Graphen der Funktion und begründe rechnerisch, ob die Funktion an einer Stelle unstetig ist.



a)
b)
c)
2
Gegeben ist die Funktion  mit
mit  Bestimme den Wert
Bestimme den Wert  für den die Funktion stetig ist.
für den die Funktion stetig ist.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
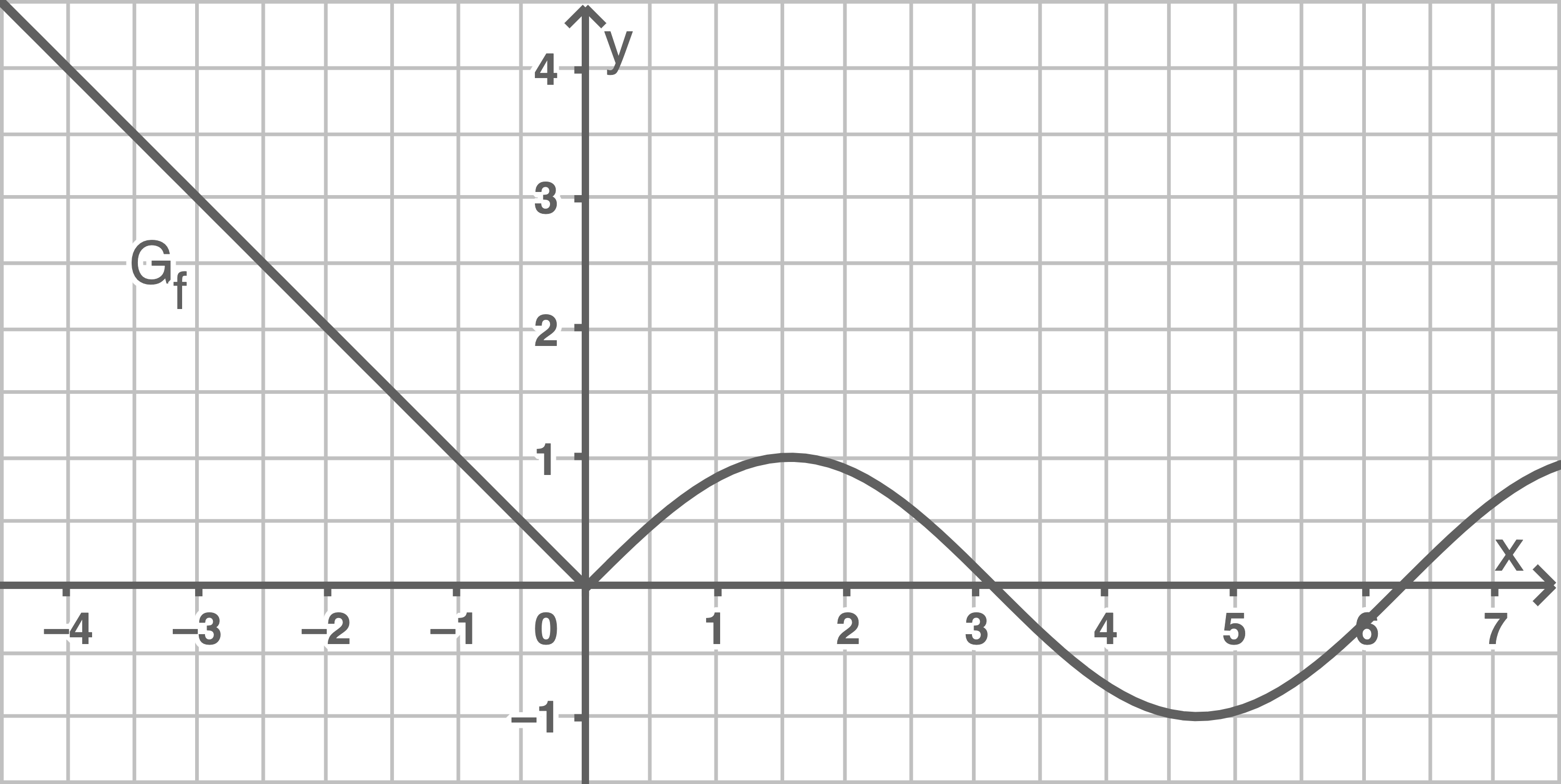
b)
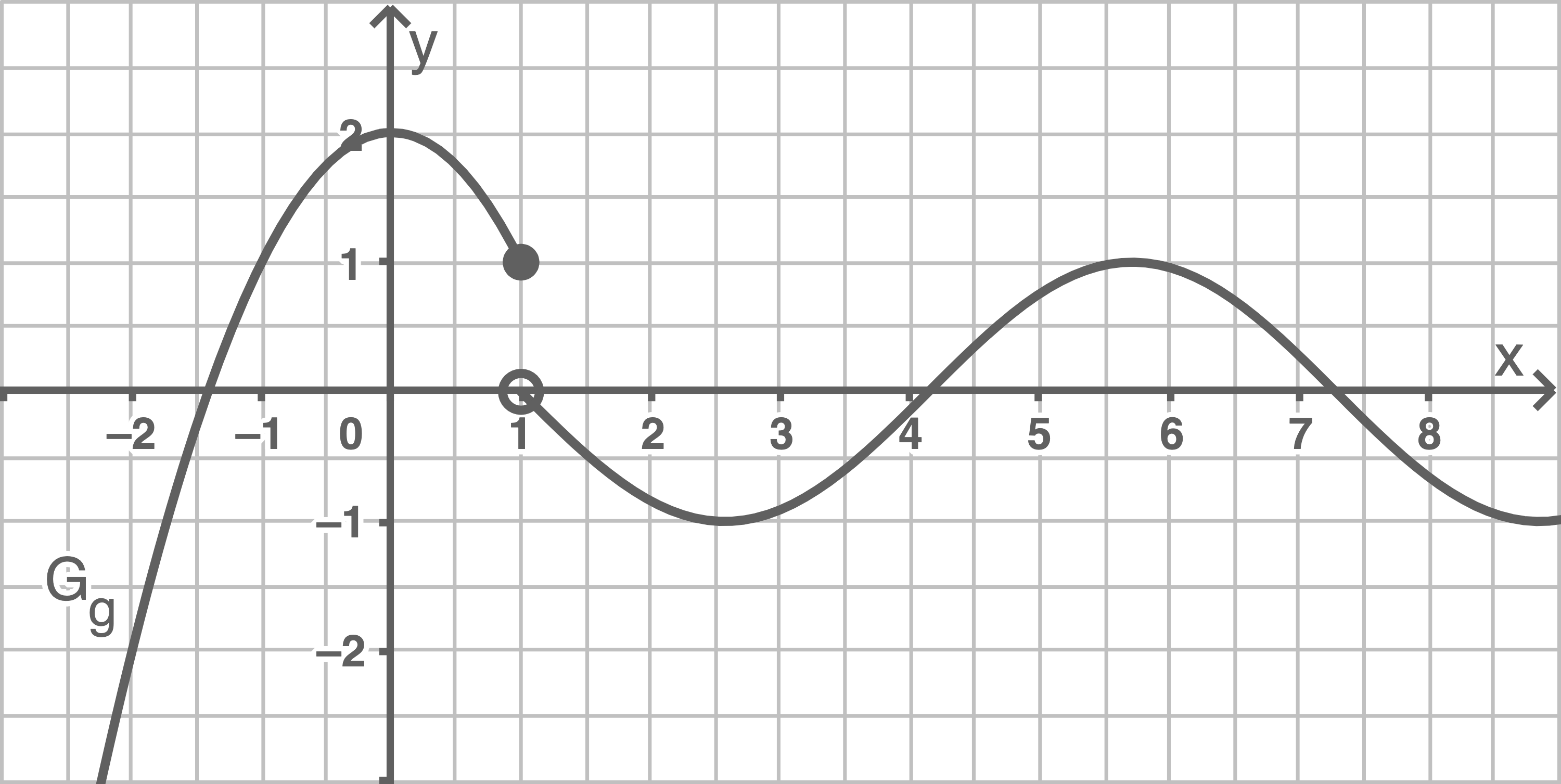
c)
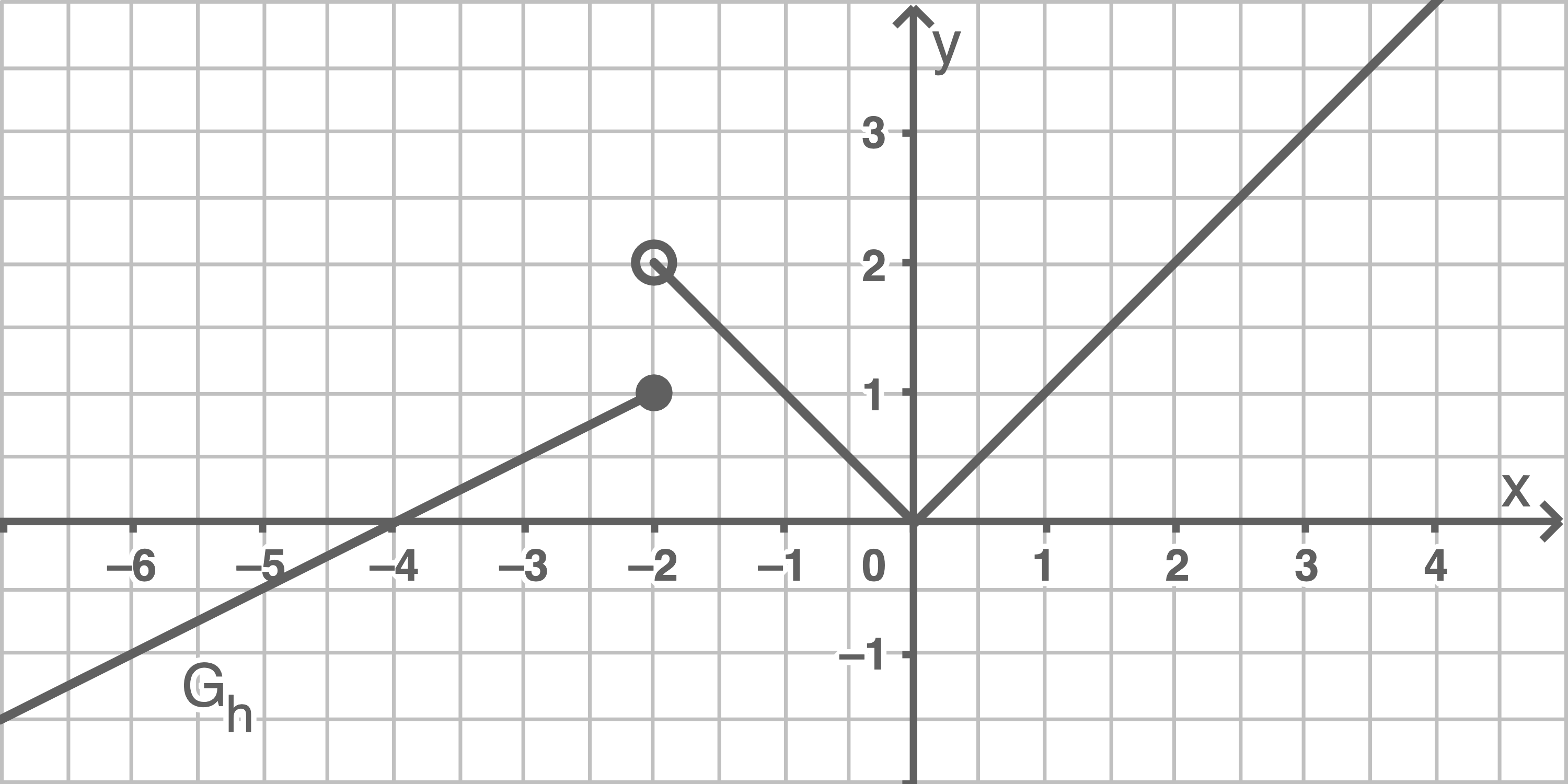
2
Damit die Funktion stetig ist, muss an der Stelle  gelten:
gelten:
![\(\begin{array}[t]{rll}
-\dfrac{3}{2}&=& a\cdot 2^2-a \\[5pt]
-\dfrac{3}{2}&=& 3a \quad \scriptsize \mid\; :3 \\[5pt]
-\dfrac{1}{2}&=& a
\end{array}\)](https://mathjax.schullv.de/11ea4de627fe18623cd34f84f0e8800513a80b4371ca912157d58d2872bec758?color=5a5a5a) Die Funktion ist für
Die Funktion ist für  stetig.
stetig.