Symmetrie von Funktionsgraphen

Definition

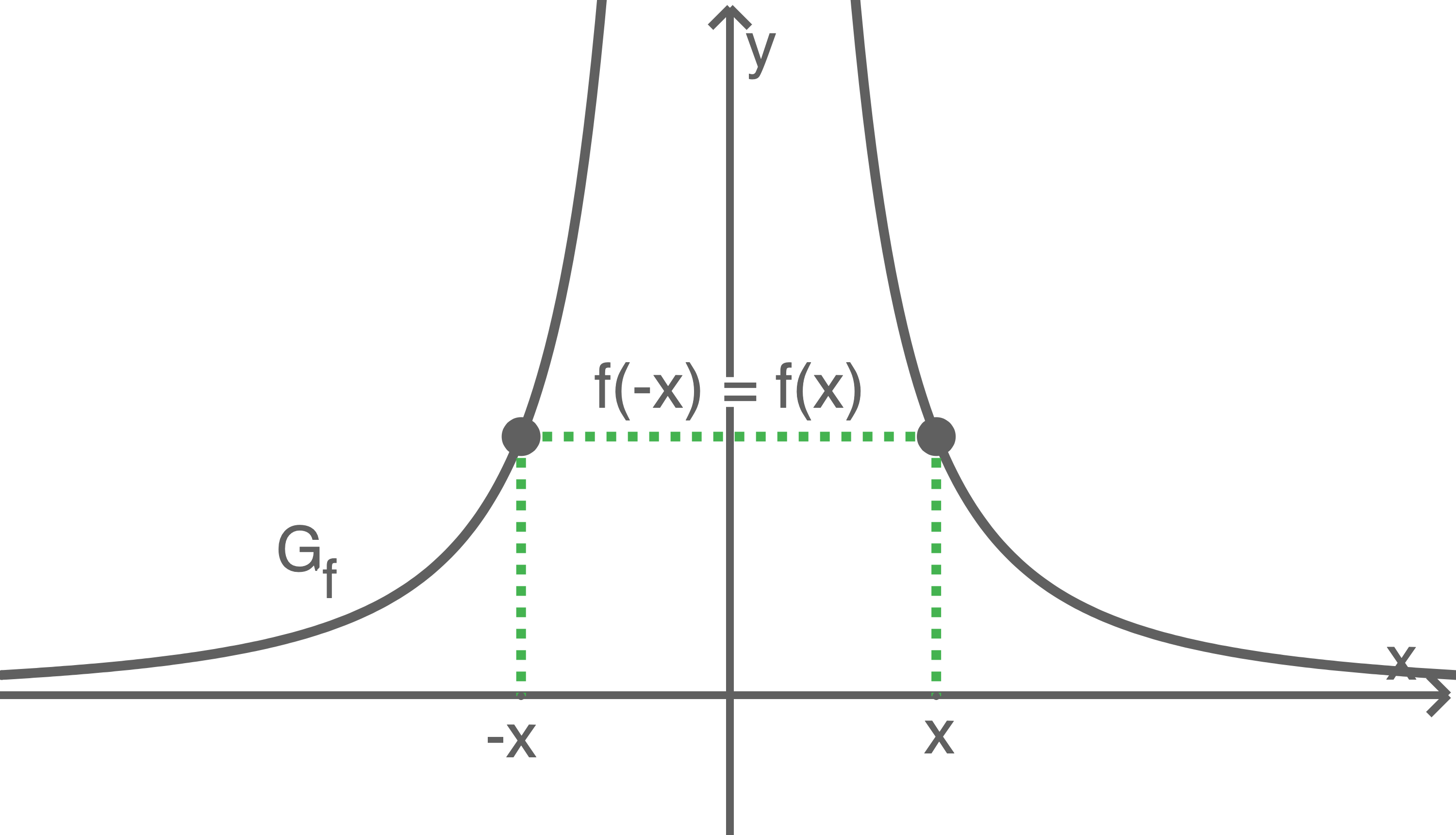
Achsensymmetrie zur $\boldsymbol{y}$ -Achse

Der Graph einer Funktion $f$ ist genau dann achsensymmetrisch zur $y$ -Achse, wenn für alle $x\in D$ gilt:

$\boldsymbol{f(-x)=f(x)}$

symmetrie von funktionsgraphen, achsensymmetrie

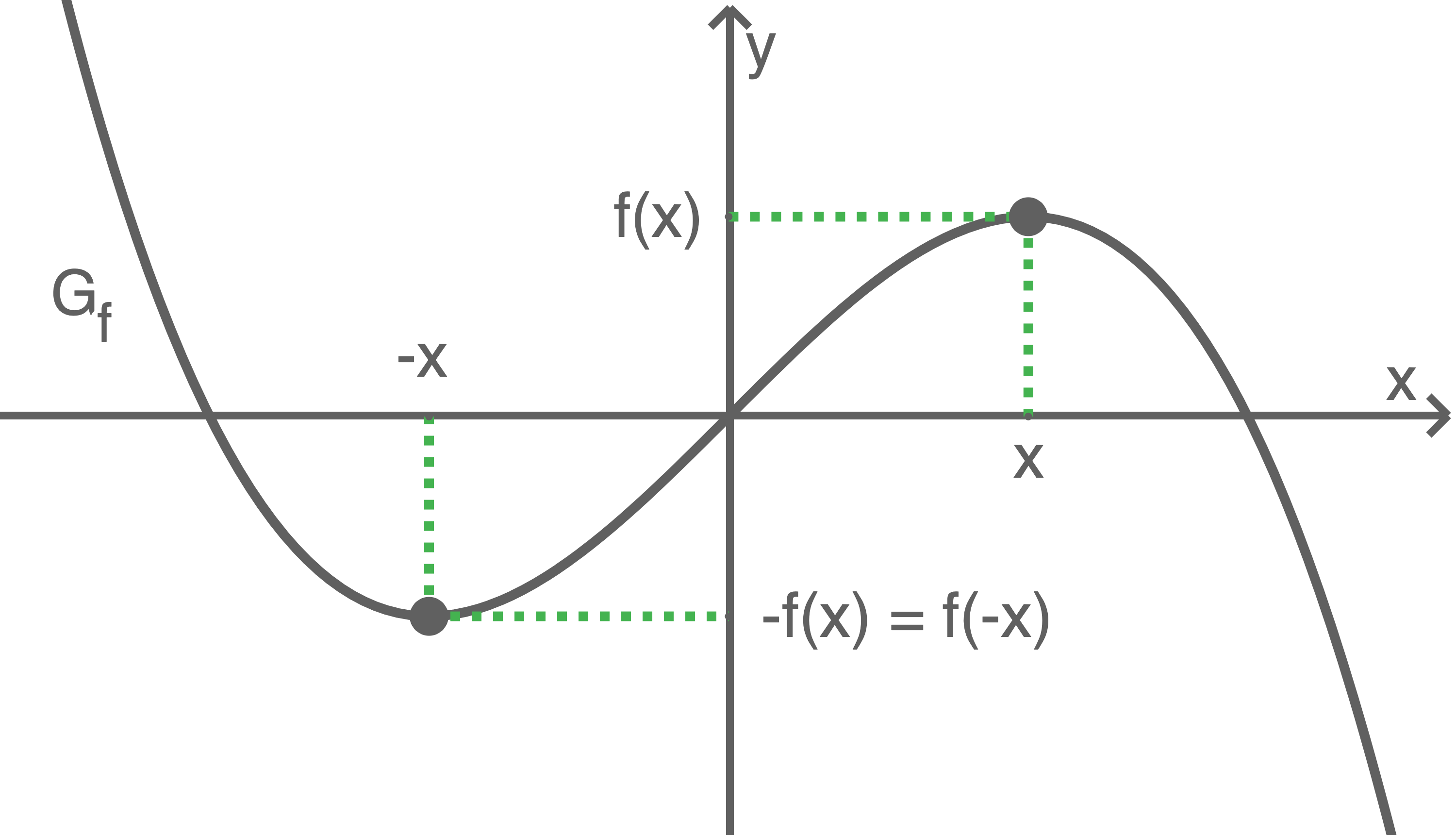
Punktsymmetrie zum Koordinatenursprung

Der Graph einer Funktion $f$ ist genau dann punktsymmetrisch zum Koordinatenursprung, wenn für alle $x\in D$ gilt:

$\boldsymbol{f(-x)=-f(x)}$

symmetrie von funktionsgraphen, punktsymmetrie

Beispiele

Ganzrationale Funktionen: $x\mapsto a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0$

Achsensymmetrisch zur $y$ -Achse, wenn im Funktionsterm nur Potenzen von $x$ mit geraden Exponenten vorkommen.
Punktsymmetrisch zum Ursprung, wenn im Funktionsterm nur Potenzen von $x$ mit ungeraden Exponenten vorkommen.

Gebrochen-rationale Funktionen: $x\mapsto \dfrac{a}{x+b}+c$

Punktsymmetrisch zum Ursprung, wenn $b=c=0$ gilt.

Trigonometrische Funktionen

Die Sinusfunktion mit $x\mapsto \sin(x)$ ist punktsymmetrisch zum Ursprung.
Die Kosinusfunktion mit $x\mapsto \cos(x)$ ist achsensymmetrisch zur $y$ -Achse.

Exponentialfunktion: $x\mapsto b\cdot a^x$

Keine Symmetrie vorhanden.