Grenzwerte von Funktionen
Definition
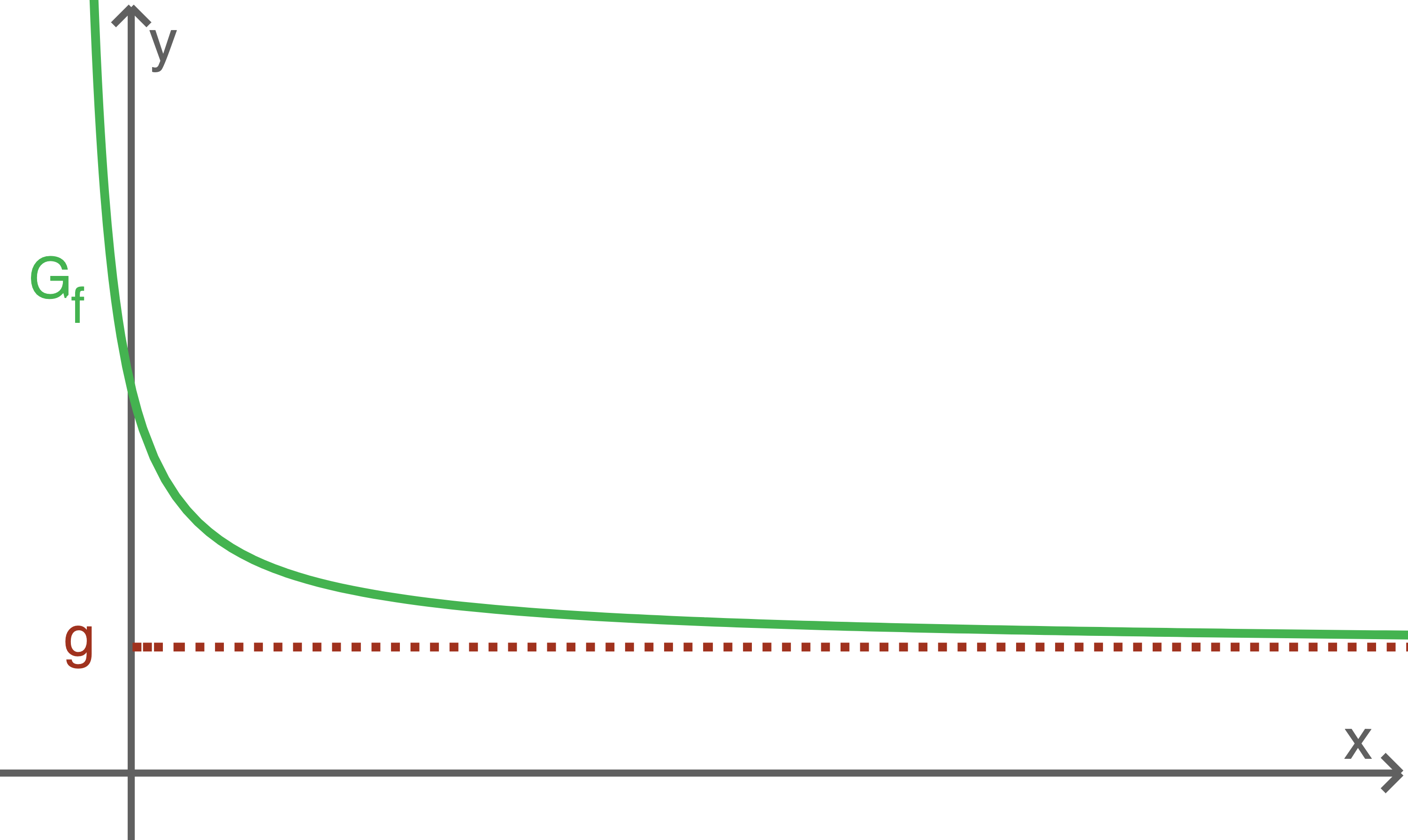
Eine Zahl  heißt Grenzwert einer Funktion
heißt Grenzwert einer Funktion  für
für  wenn sich die Funktionswerte
wenn sich die Funktionswerte  für wachsende Werte von
für wachsende Werte von  der Zahl
der Zahl  beliebig weit annähern. Man schreibt:
beliebig weit annähern. Man schreibt:
 Der Grenzwert für
Der Grenzwert für  ist analog definiert.
Besitzt eine Funktion für
ist analog definiert.
Besitzt eine Funktion für  bzw.
bzw.  einen Grenzwert, so heißt die Funktion konvergent. Funktionen, die keinen solchen Grenzwert besitzen, nennt man divergent.
einen Grenzwert, so heißt die Funktion konvergent. Funktionen, die keinen solchen Grenzwert besitzen, nennt man divergent.
Beispiel
Die Funktion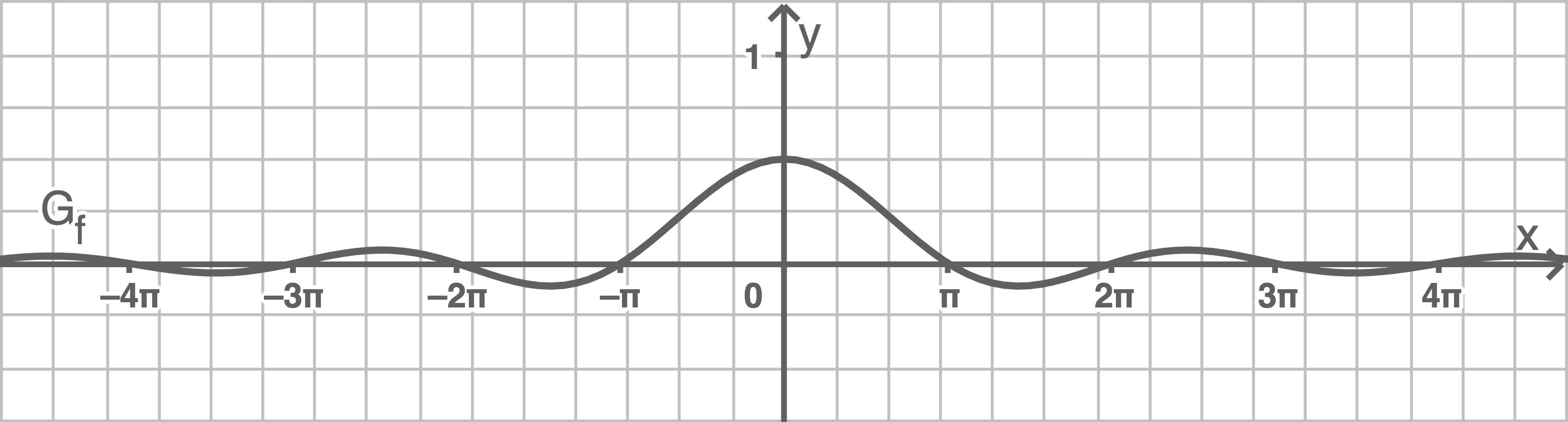
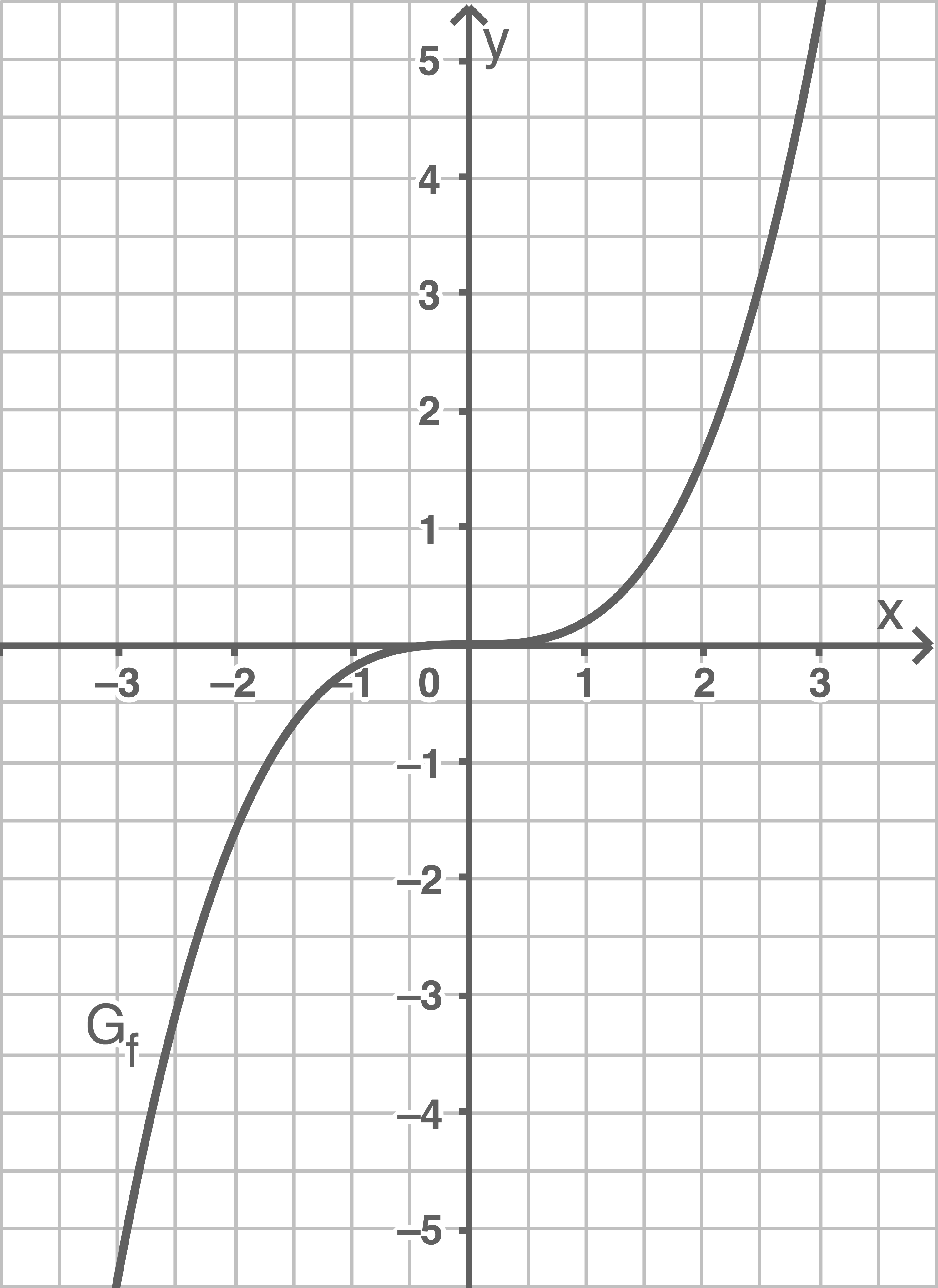
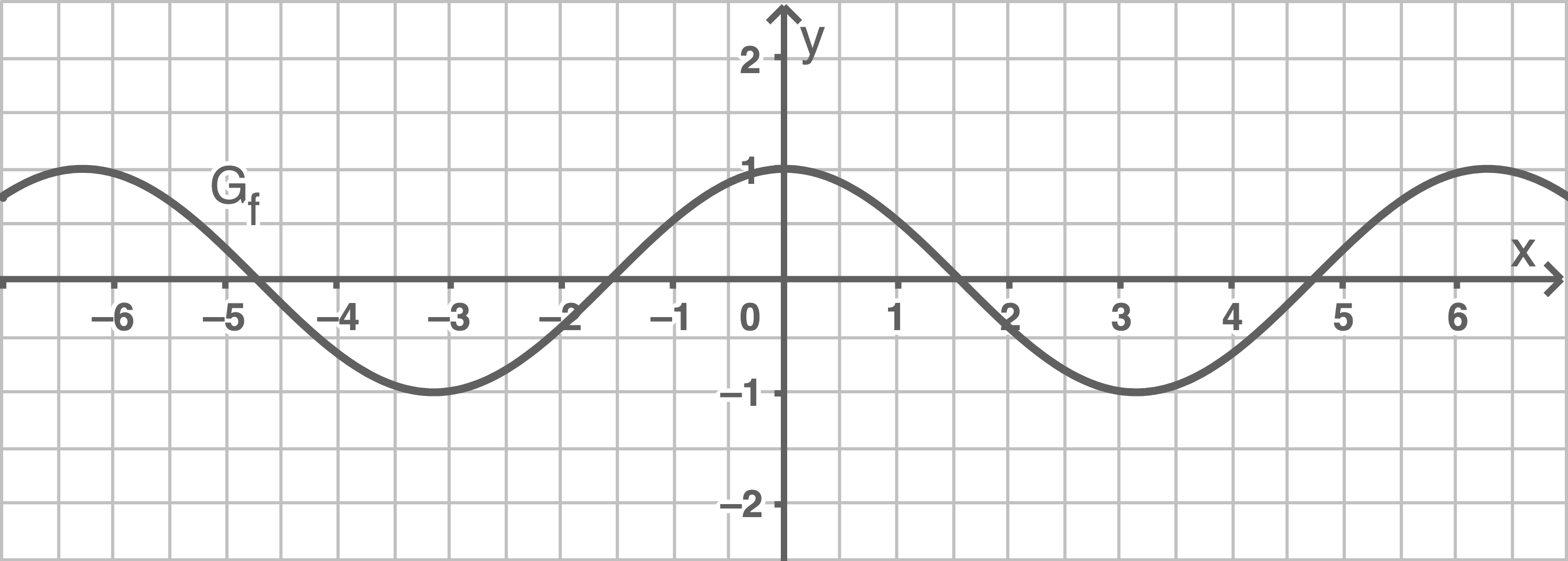
1
Skizziere den Graphen der Funktion und gib, falls möglich,  und
und  an.
an.






a)
b)
c)
d)
e)
f)
2
Gib eine Funktion mit den angegebenen Eigenschaften an.
a)
Die Funktion divergiert für  gegen
gegen  und für
und für  gegen
gegen 
b)
Die Funktion konvergiert für  und
und  gegen 3.
gegen 3.
c)
Die Funktion divergiert für  und
und  nimmt aber nur Werte zwischen
nimmt aber nur Werte zwischen  und
und  an.
an.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
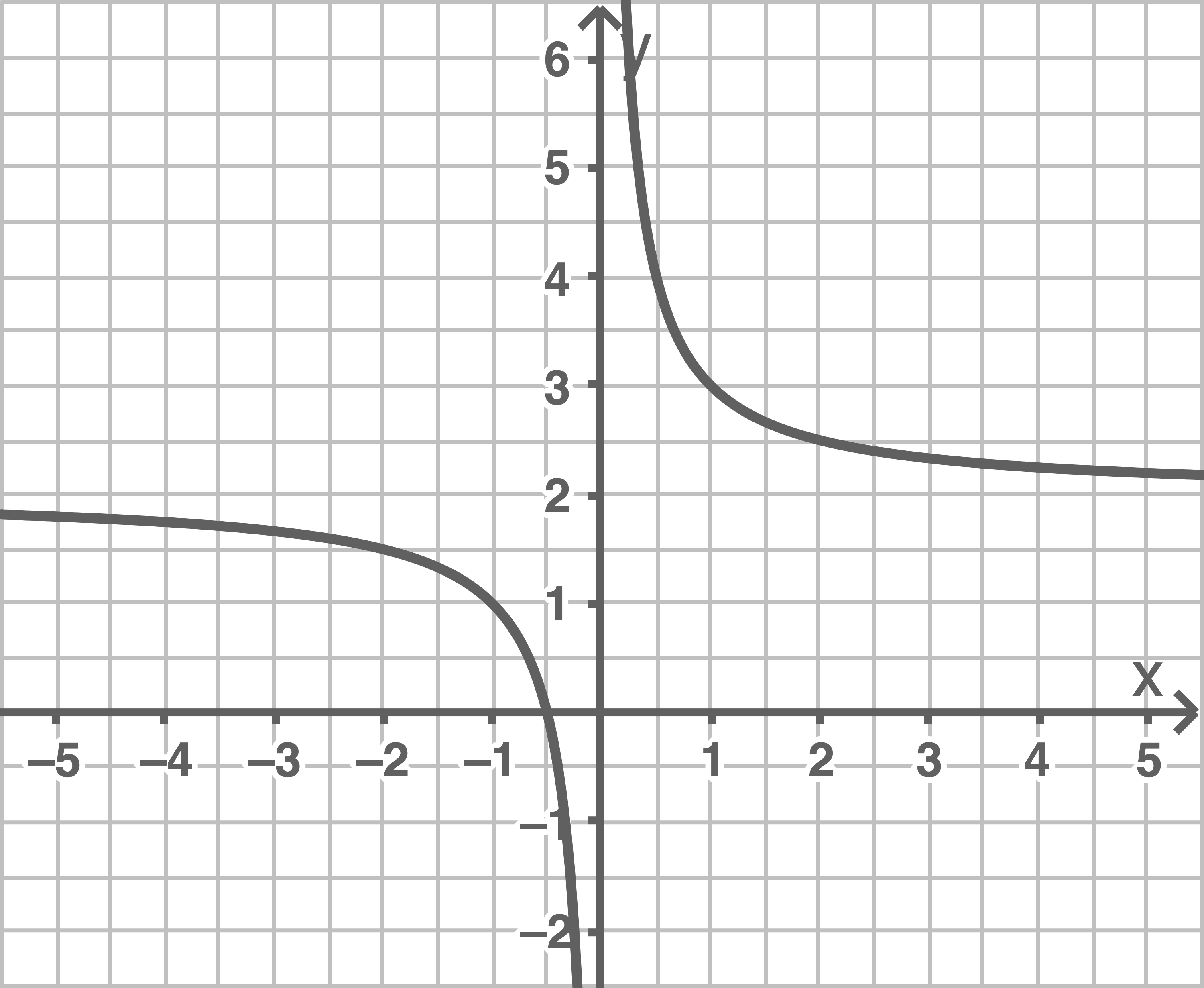
b)
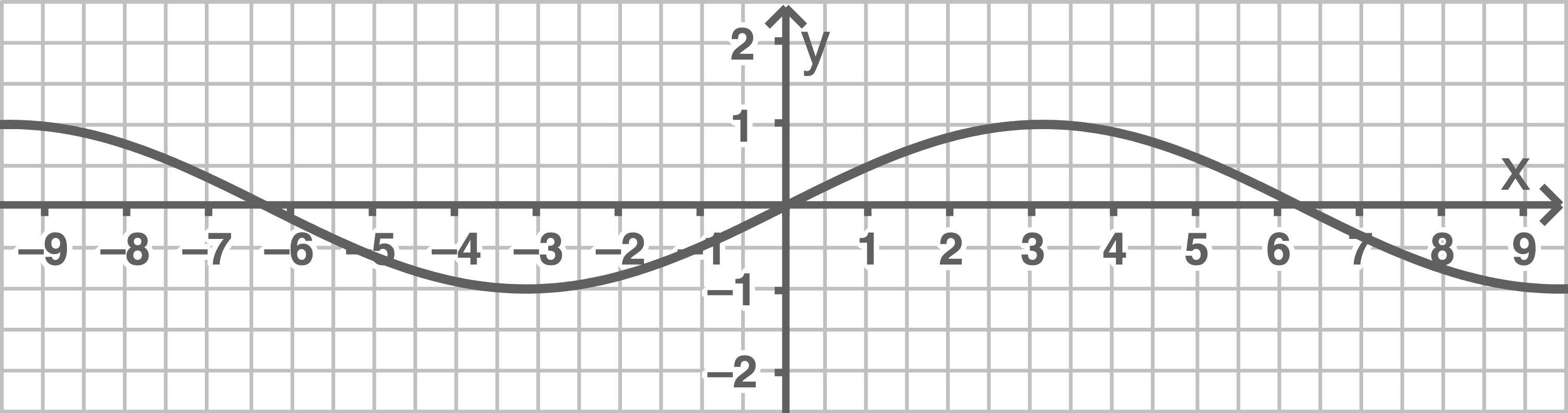
c)
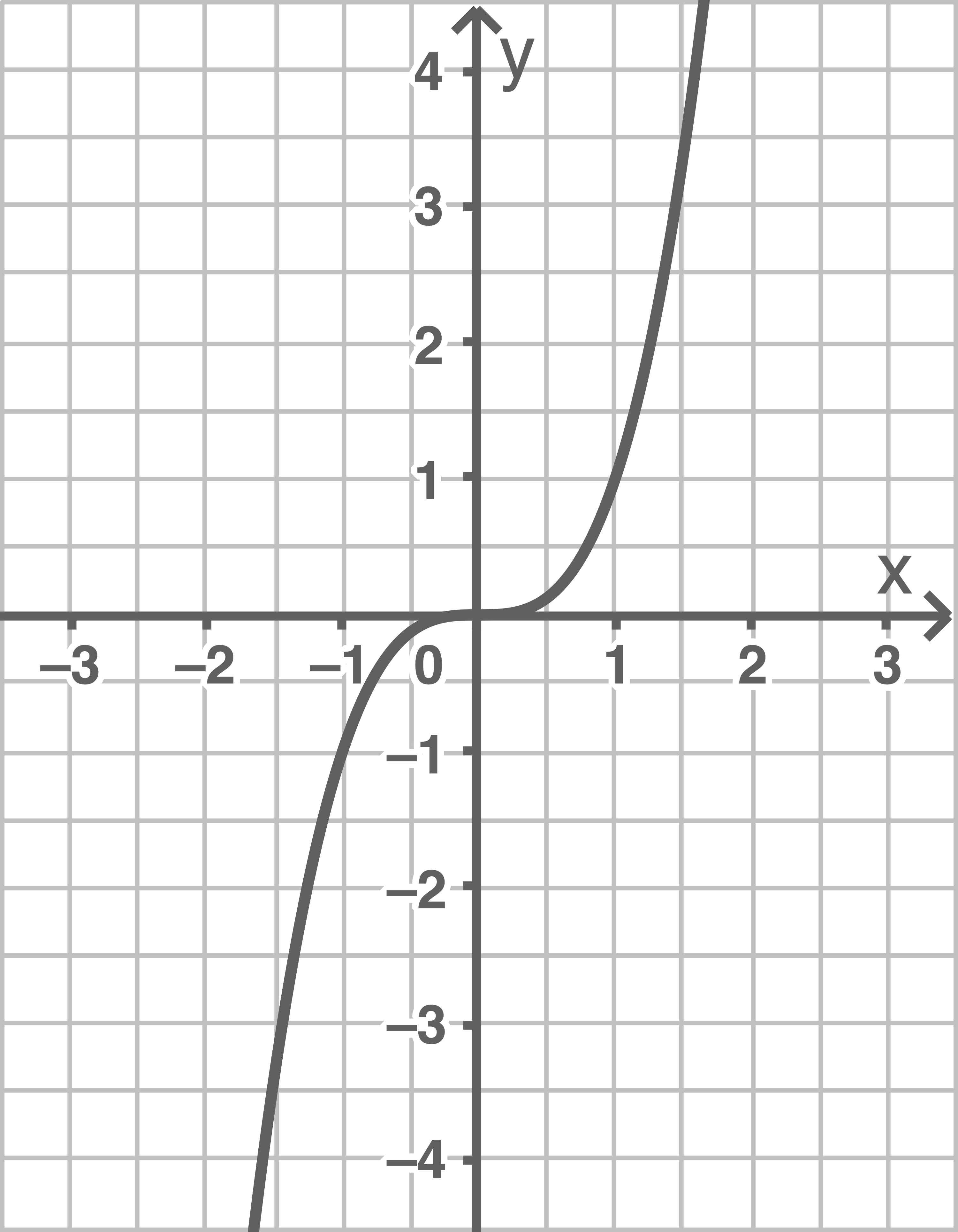
d)
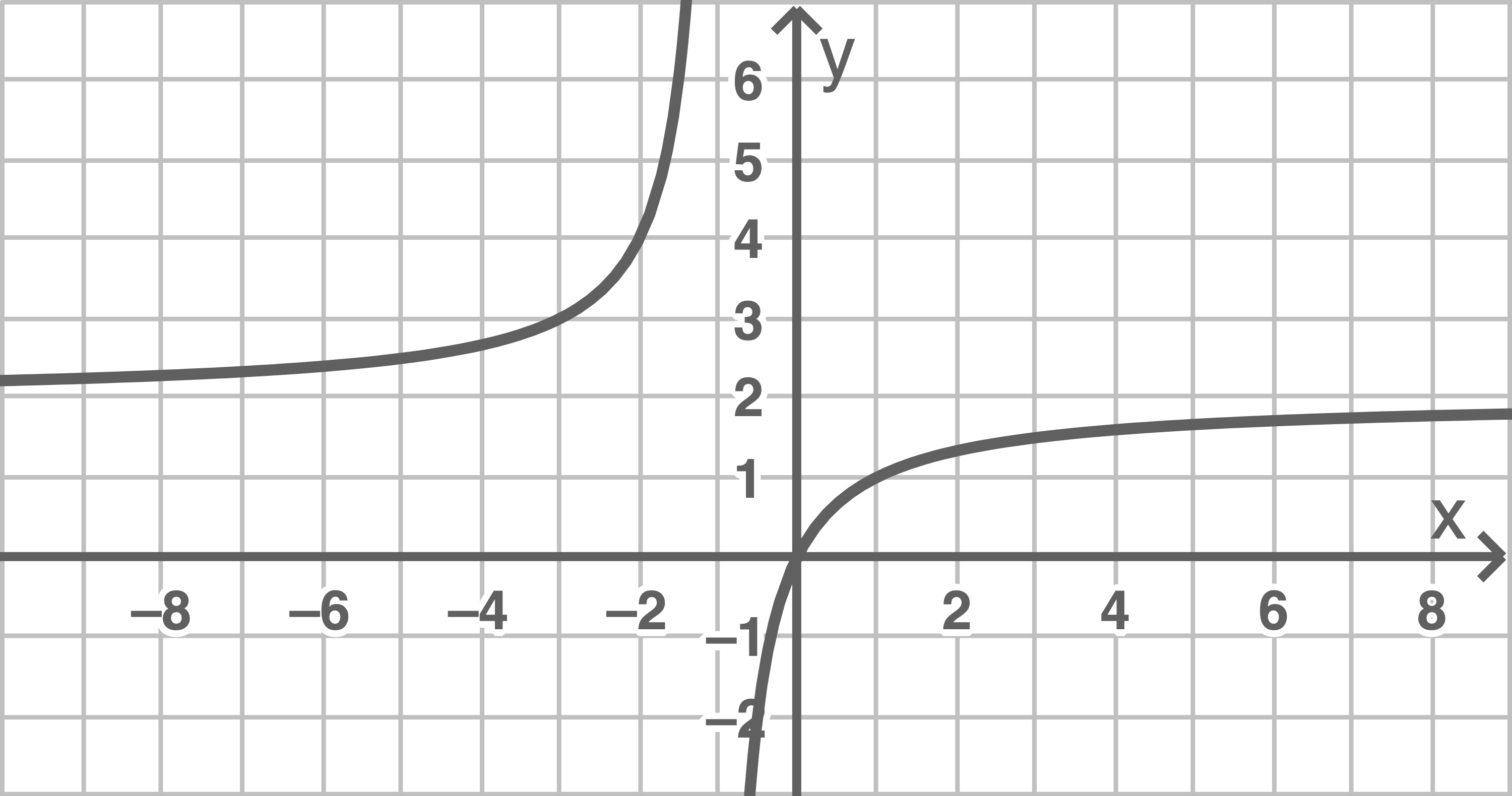
e)
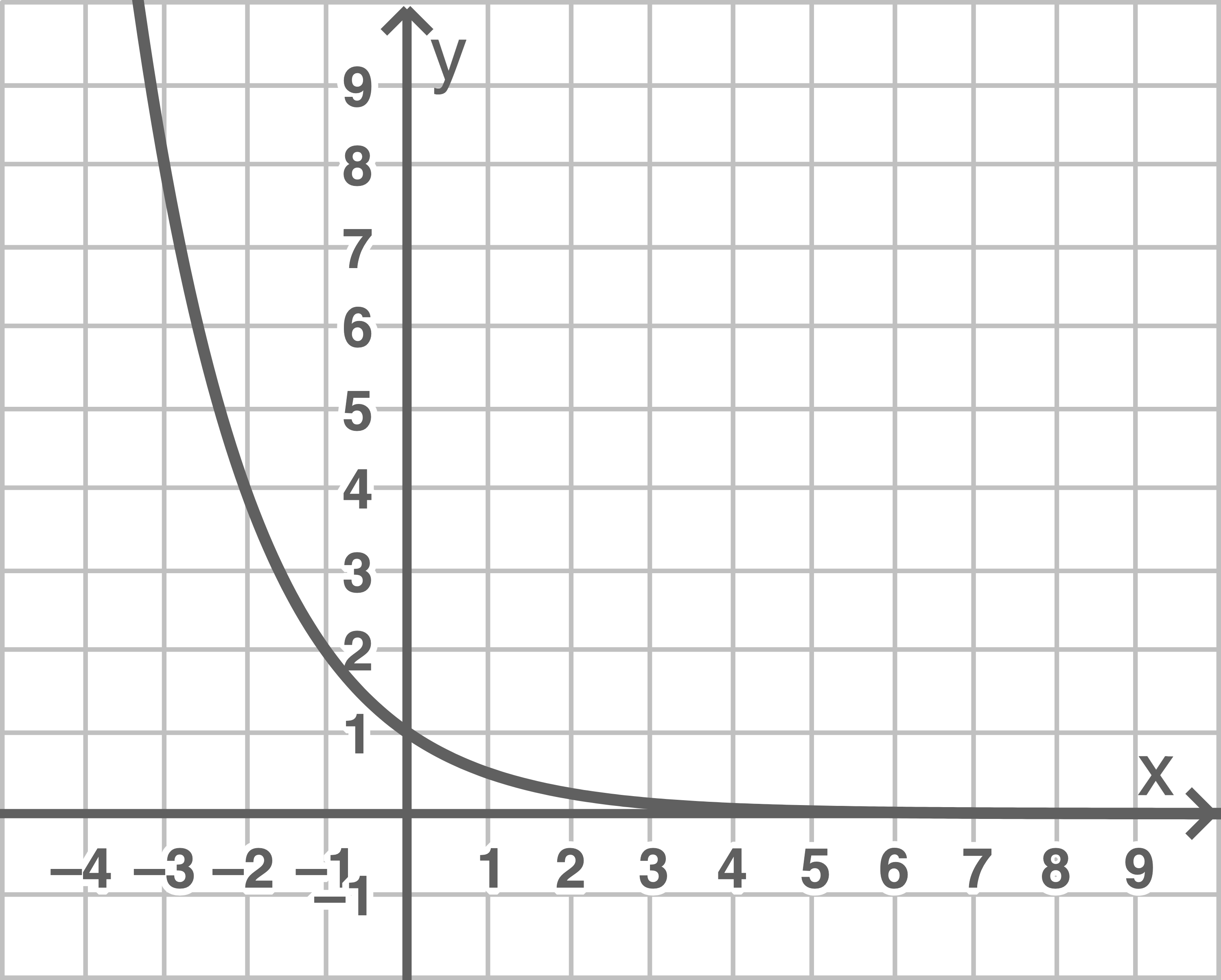
f)
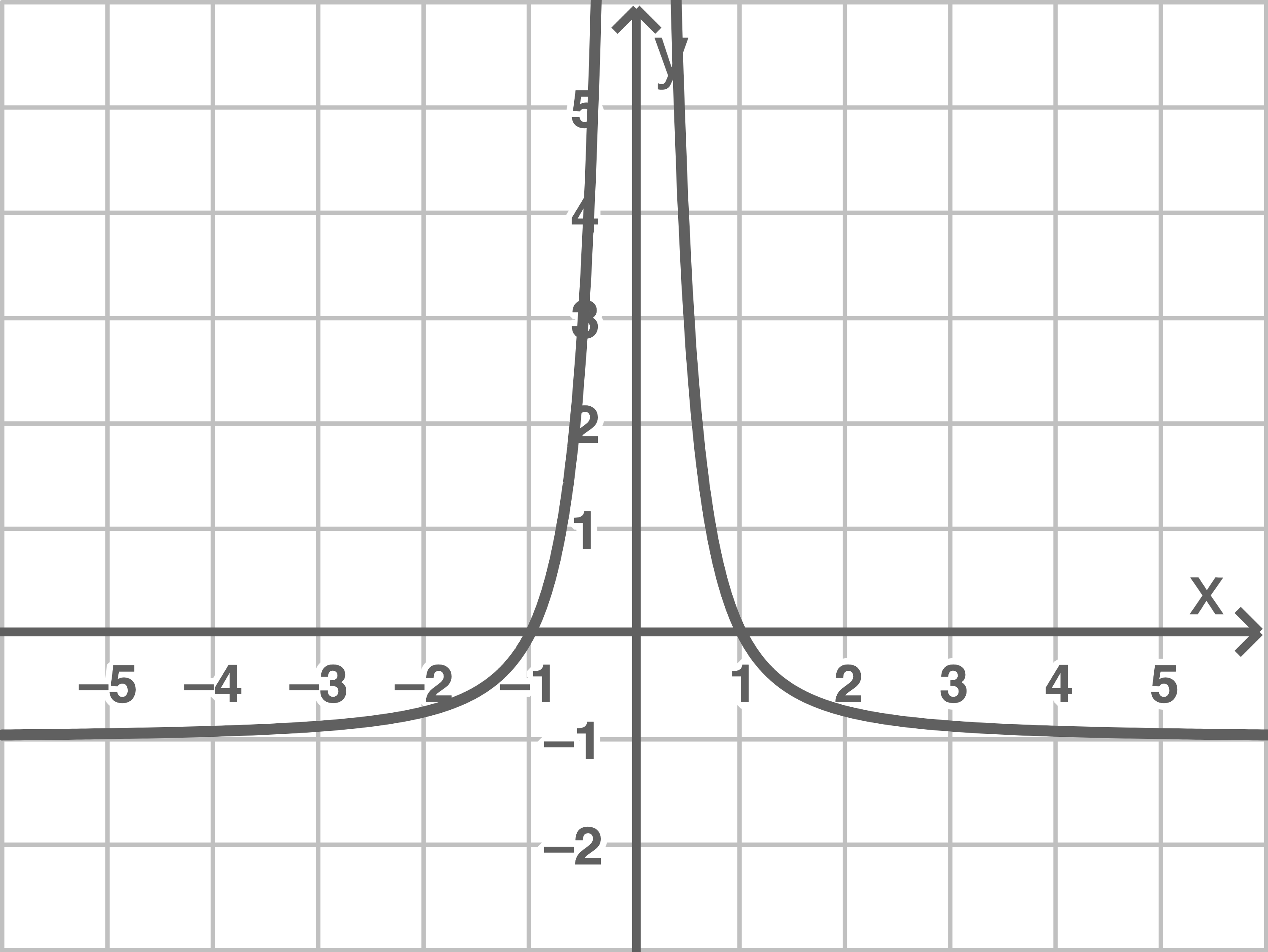
2
a)
b)
c)