Newton-Verfahren
Definition
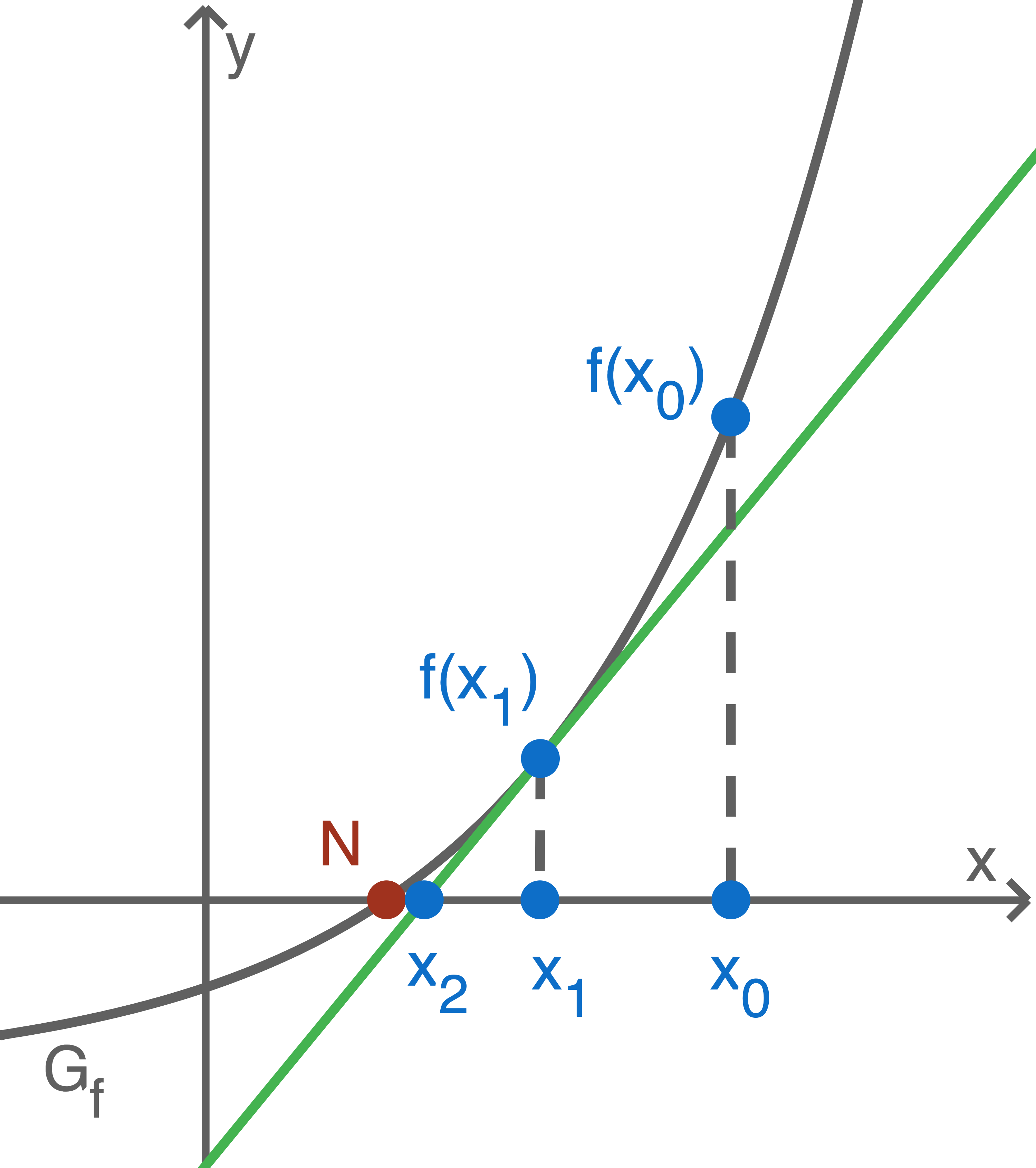
Mit dem Newton-Verfahren kann näherungsweise eine Nullstelle einer differenzierbaren Funktion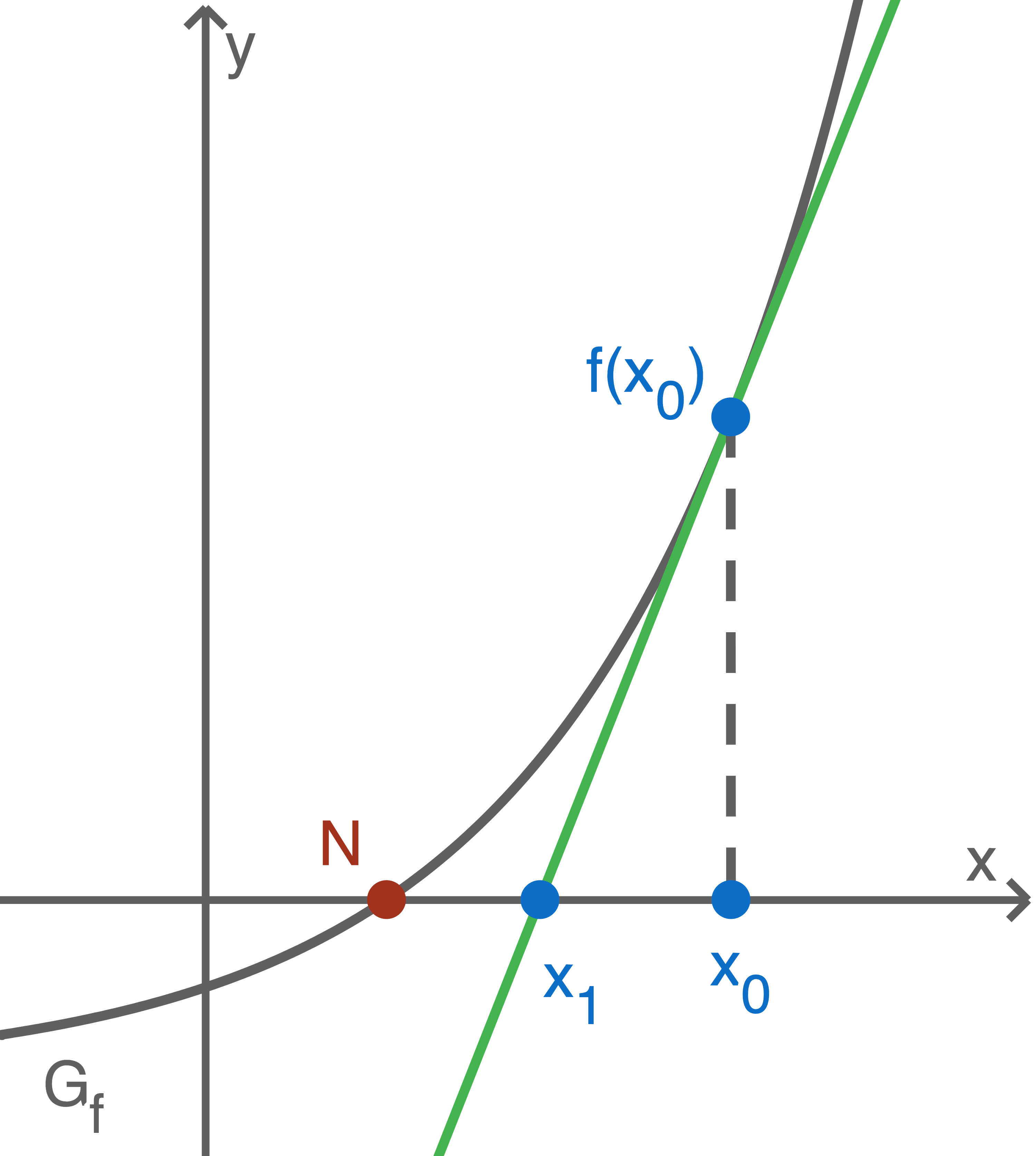
- Ein
-Wert liegt nicht im Definitionsbereich.
- Die
-Werte werden beliebig groß.
- Die
-Werte nähern sich nicht der gesuchten, sondern einer anderen Nullstelle an.
1
Die Funktion  mit
mit  ist in der Abbildung dargestellt.
ist in der Abbildung dargestellt.
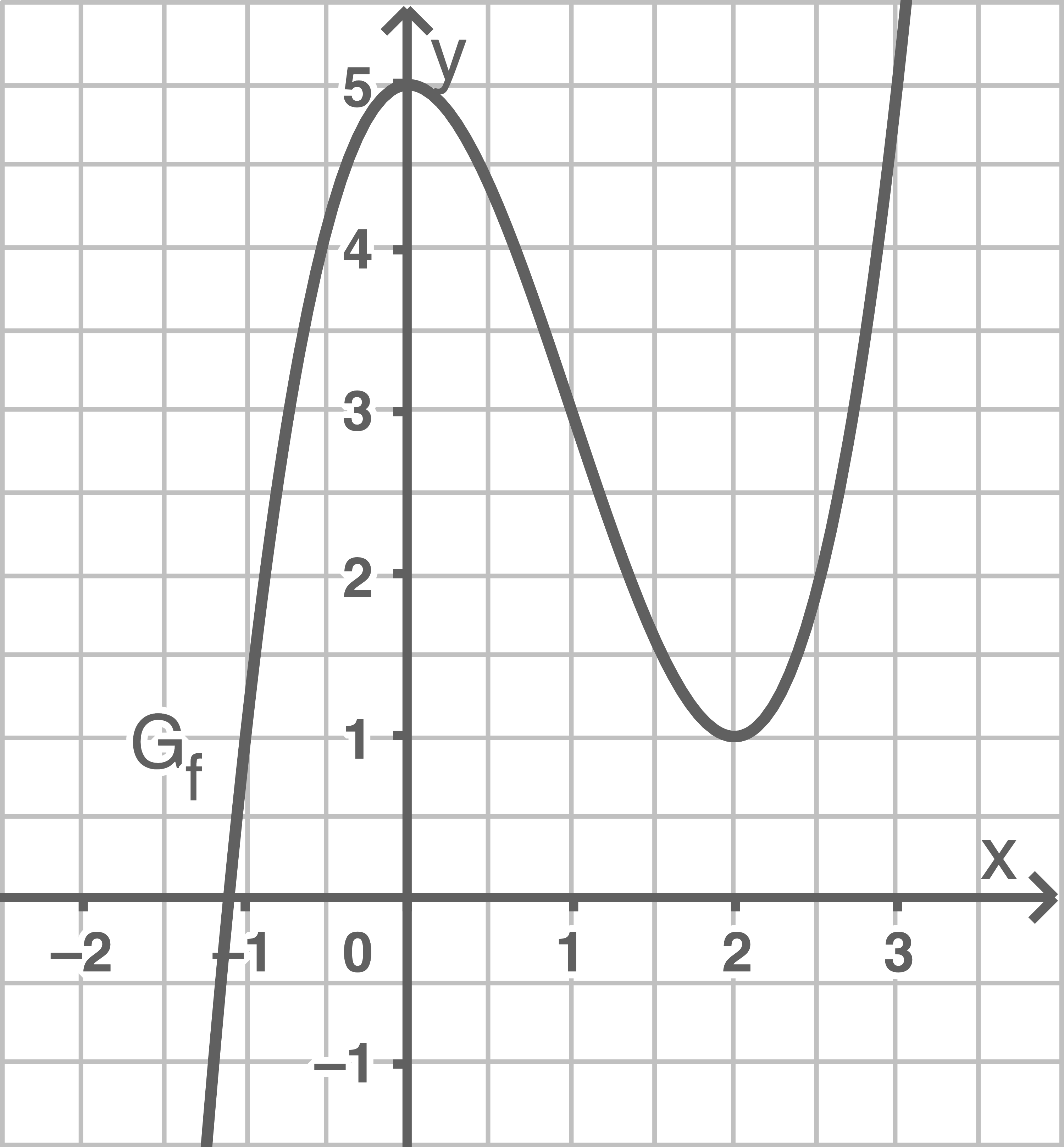
a)
Gib zwei Startwerte an, für die das Newton-Verfahren nicht zielführend ist.
b)
Begründe anhand des Graphen, warum die Wahl der Startwerte zu keinem Ergebnis führt.
c)
Begründe anhand der Iterationsvorschrift, warum die Wahl der Startwerte zu keinem Ergebnis führt.

2
Die Funktion  hat genau eine Nullstelle. Berechne mit zwei Schritten des Newton-Verfahrens einen Näherungswert für die Nullstelle mit dem angegebenen Startwert.
hat genau eine Nullstelle. Berechne mit zwei Schritten des Newton-Verfahrens einen Näherungswert für die Nullstelle mit dem angegebenen Startwert.




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Das Newton-Verfahren führt für die Startwerte  und
und  zu keinem Ergebnis.
zu keinem Ergebnis.
b)
An beiden Stellen verläuft die Tangente an den Graphen von  parallel zur
parallel zur  -Achse. Diese wird also nie geschnitten und es ergibt sich kein Näherungswert
-Achse. Diese wird also nie geschnitten und es ergibt sich kein Näherungswert 
c)
Beide Stellen sind Extremstellen der Funktion  es gilt also
es gilt also  Damit ergibt sich im ersten Schritt des Newton-Verfahrens im Nenner der Wert
Damit ergibt sich im ersten Schritt des Newton-Verfahrens im Nenner der Wert 
2
a)
b)
c)
d)