Definitionsmenge und Nullstellen
Definition
Eine Funktion der FormDefinitionsmenge
Die Definitionsmenge einer gebrochen-rationalen Funktion
Bei einer gebrochen-rationalen Funktion  in der Form
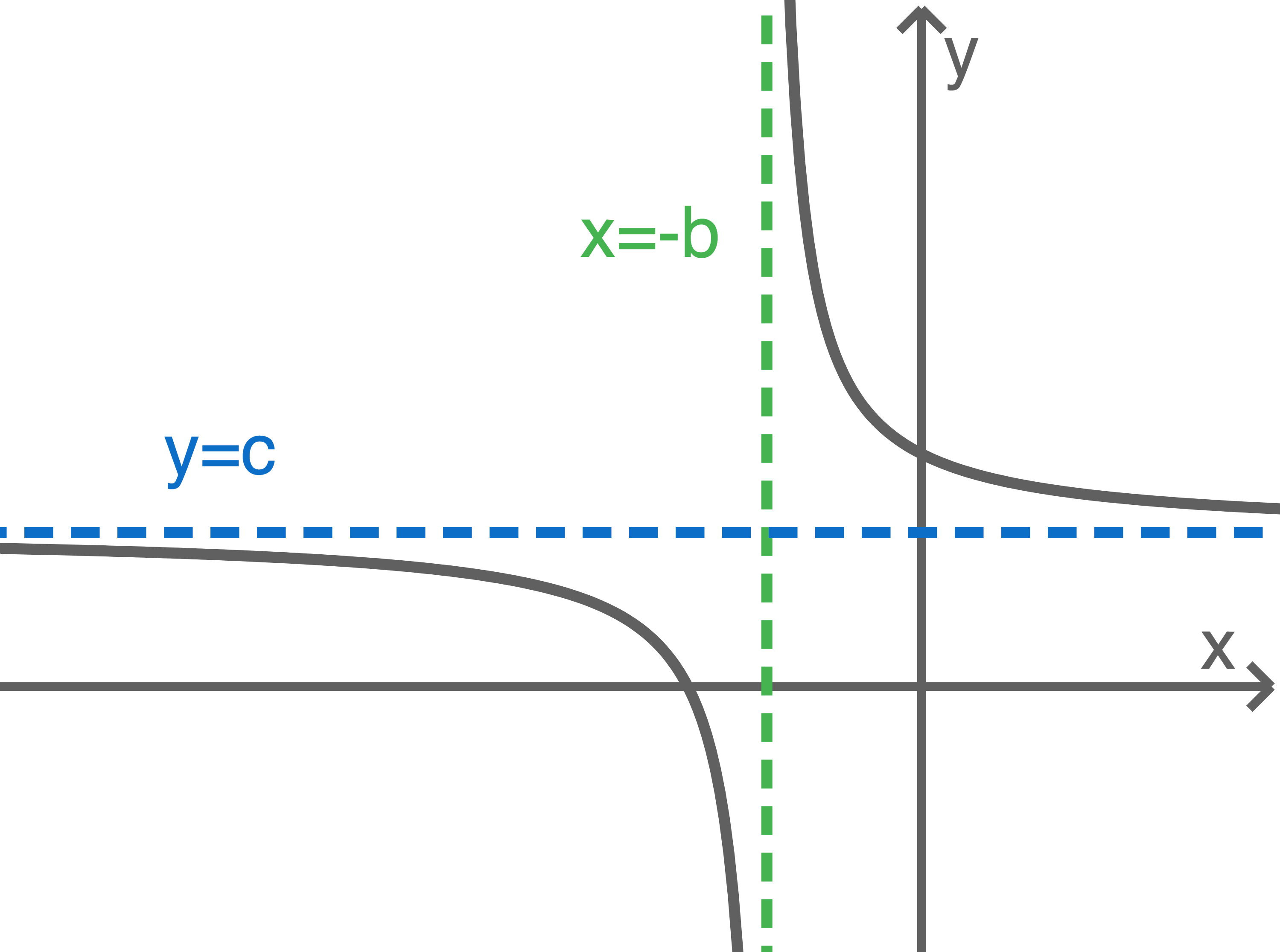
in der Form  können die Definitionsmenge und die Gleichungen der Asymptoten des Funktionsgraphen direkt angegeben werden:
Definitionsbereich:
können die Definitionsmenge und die Gleichungen der Asymptoten des Funktionsgraphen direkt angegeben werden:
Definitionsbereich:  Asymptoten:
Asymptoten: 
Nullstellen
Die Nullstellen einer gebrochen-rationalen Funktion
1
Bestimme die Definitionsmenge der Funktion 




a)
b)
c)
d)
2
Bestimme die Nullstellen der Funktion 




a)
b)
c)
d)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
c)
d)
2
a)
b)
c)
Funktion umformen:
![\(\begin{array}[t]{rll}
\dfrac{1}{x-4}+2&=& \dfrac{1}{x-4}+\dfrac{2(x-4)}{(x-4)} \\[5pt]
&=& \dfrac{1+2(x-4)}{x-4} \\[5pt]
&=& \dfrac{1+2x-8}{x-4} \\[5pt]
&=& \dfrac{2x-7}{x-4}
\end{array}\)](https://mathjax.schullv.de/1999e9e6d733a3f16fbce80215a2a49b0089ec34e0fe96a20855b35d65ad3059?color=5a5a5a) Nullstellen berechnen:
Nullstellen berechnen:
![\(\begin{array}[t]{rll}
2x-7&=& 0 \quad \scriptsize \mid\; +7\\[5pt]
2x&=& 7 \quad \scriptsize \mid\; :2\\[5pt]
x&=& 3,5
\end{array}\)](https://mathjax.schullv.de/99fda0d1e715591a37849bdebf7fc01bde43457a7e302f4990196866c25d370d?color=5a5a5a) Die Funktion
Die Funktion  hat die Nullstelle
hat die Nullstelle 
d)
Funktion umformen:
![\(\begin{array}[t]{rll}
\dfrac{0,4}{x+1}-2&=& \dfrac{0,4}{x+1}-\dfrac{2(x+1)}{(x+1)} \\[5pt]
&=& \dfrac{0,4-2(x+1)}{x+1} \\[5pt]
&=& \dfrac{0,4-2x-2}{x+1} \\[5pt]
&=& \dfrac{-2x-1,6}{x+1}
\end{array}\)](https://mathjax.schullv.de/f6750e94d148523201455b87324f65823df09163f6c9dd3821333bd901a34e42?color=5a5a5a) Nullstellen berechnen:
Nullstellen berechnen:
![\(\begin{array}[t]{rll}
-2x-1,6&=& 0 \quad \scriptsize \mid\; +1,6\\[5pt]
-2x&=& 1,6 \quad \scriptsize \mid\; :(-2) \\[5pt]
x&=& -0,8
\end{array}\)](https://mathjax.schullv.de/624282a8b4cc4eb9b1734dfa3443f7025adb9fcdf85d67afddae75a81b5f46f8?color=5a5a5a) Die Funktion
Die Funktion  hat die Nullstelle
hat die Nullstelle 