Differenzierbarkeit
Definition
Wenn für eine Funktion  an der Stelle
an der Stelle  der Differentialquotient
der Differentialquotient  existiert, dann heißt
existiert, dann heißt  an der Stelle
an der Stelle  differenzierbar.
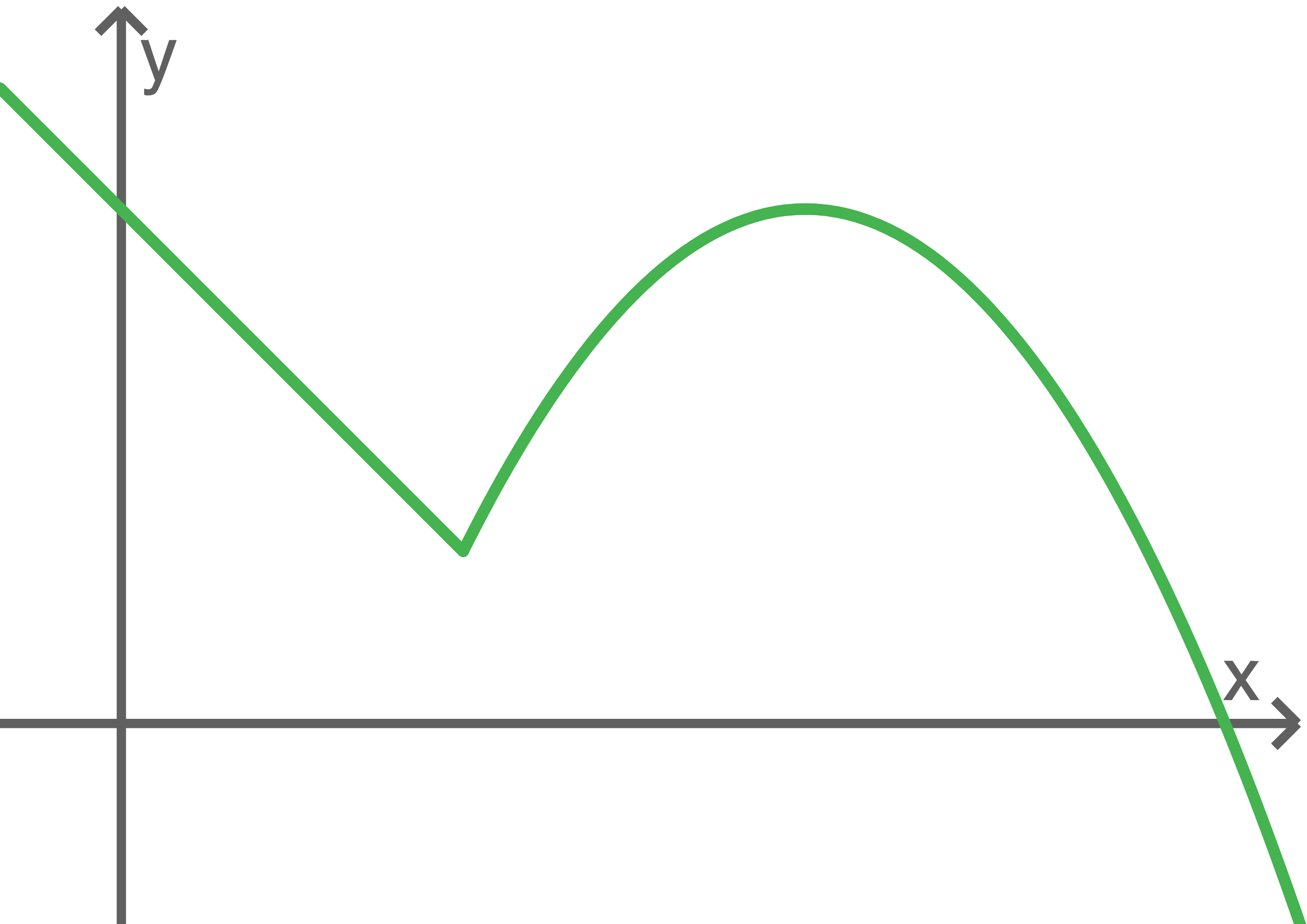
Hat der Graph einer Funktion einen „Knick“ wie in der Abbildung, so existiert an dieser Stelle keine Tangente und somit auch keine Ableitung.
differenzierbar.
Hat der Graph einer Funktion einen „Knick“ wie in der Abbildung, so existiert an dieser Stelle keine Tangente und somit auch keine Ableitung.
Zusammenhang zwischen Differenzierbarkeit und Stetigkeit
Ist eine Funktion an der Stelle- differenzierbar, so ist sie an der Stelle
stetig.
- nicht stetig, so ist sie an der Stelle
nicht differenzierbar.
- stetig, so folgt daraus nicht, dass sie an der Stelle
differenzierbar ist.
Beispiel
Die Betragsfunktion
1
a)
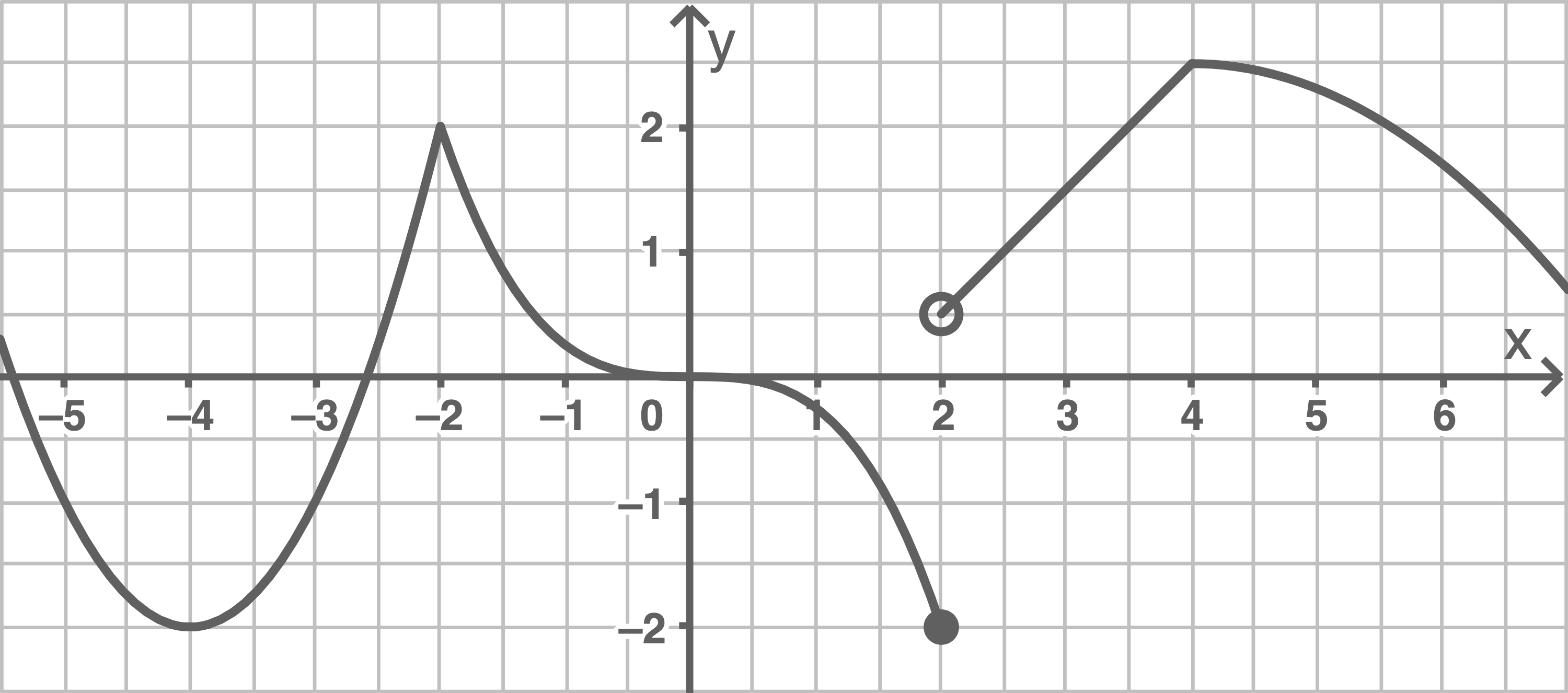
Dargestellt ist der Graph einer Funktion  Gib die Stellen an, an denen die Funktion
Gib die Stellen an, an denen die Funktion  nicht differenzierbar ist und begründe.
nicht differenzierbar ist und begründe.

b)
Skizziere den Graphen einer Funktion, die an der Stelle
nicht stetig ist,
stetig, aber nicht differenzierbar ist,
stetig und differenzierbar ist.
2
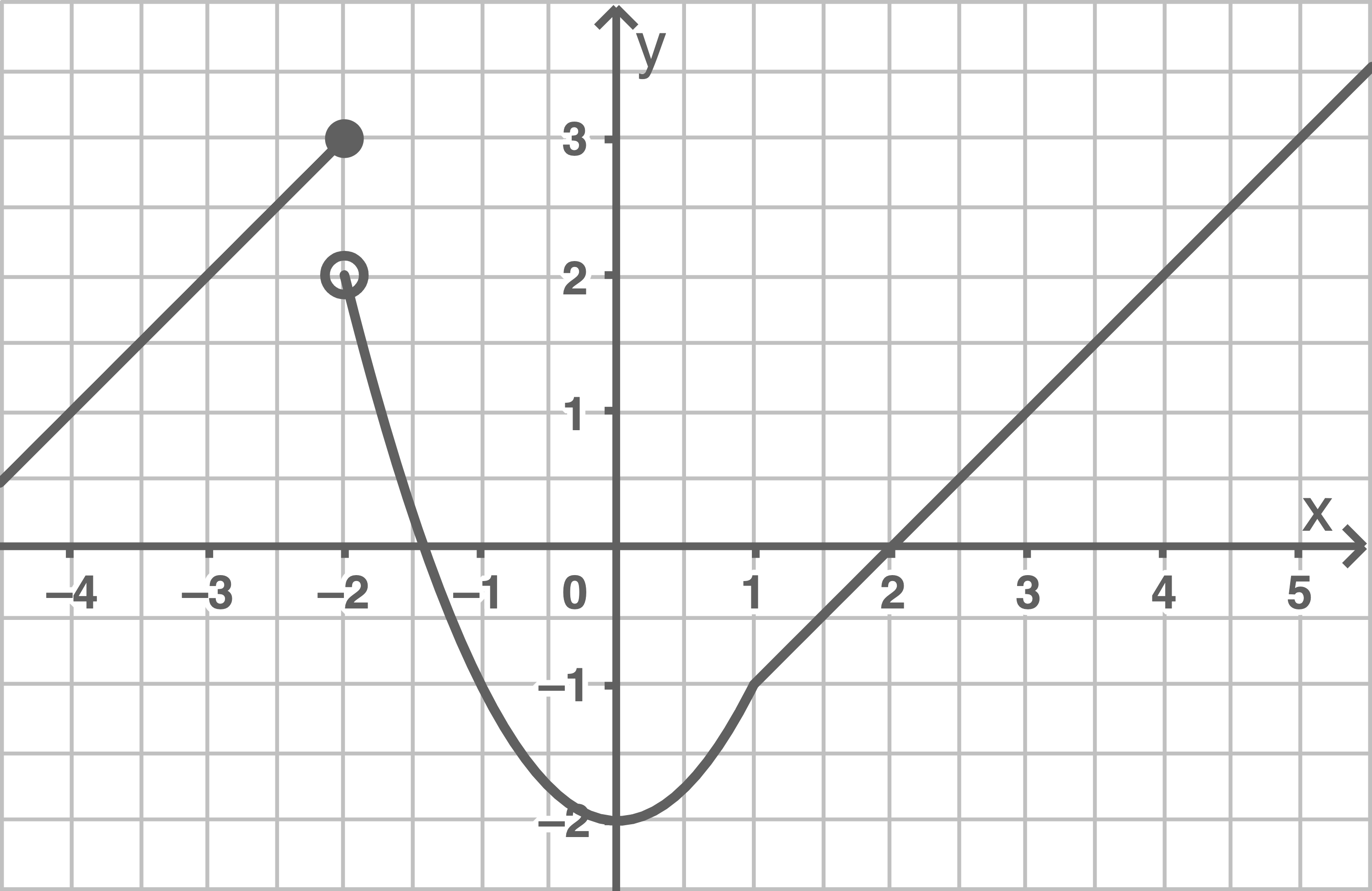
Gegeben ist der Graph einer Funktion  mit
mit 
a)
Schreibe den Funktionsterm ohne Betrag als abschnittsweise definierte Funktion.
b)
Untersuche die Funktion  rechnerisch auf Differenzierbarkeit an den Stellen
rechnerisch auf Differenzierbarkeit an den Stellen  und
und 
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
An den Stellen  und
und  hat der Graph der Funktion einen Knick und ist daher dort nicht differenzierbar.
An der Stelle
hat der Graph der Funktion einen Knick und ist daher dort nicht differenzierbar.
An der Stelle  macht der Graph einen Sprung. An dieser Stelle ist die Funktion daher nicht stetig und somit auch nicht differenzierbar.
macht der Graph einen Sprung. An dieser Stelle ist die Funktion daher nicht stetig und somit auch nicht differenzierbar.
b)
2
a)
b)
Untersuchung auf Differenzierbarkeit an der Stelle 
 an der Stelle
an der Stelle  nicht differenzierbar.
Untersuchung auf Differenzierbarkeit an der Stelle
nicht differenzierbar.
Untersuchung auf Differenzierbarkeit an der Stelle 
 an der Stelle
an der Stelle  nicht differenzierbar.
nicht differenzierbar.
Linksseitiger Grenzwert:
![\(\begin{array}[t]{rll}
&\lim\limits_{h\to 0\\h\lt 0}\dfrac{f(-2+h)-f(-2)}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0}\dfrac{\dfrac{1}{2}(-2+h)^2-2-0}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0}\dfrac{\dfrac{1}{2}(4-4h+h^2)-2}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0}\dfrac{2-2h+\dfrac{h^2}{2}-2}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0}\dfrac{h\left(-2+\dfrac{h}{2}\right)}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0} -2+\dfrac{h}{2} \\[5pt]
=& -2
\end{array}\)](https://mathjax.schullv.de/996d553df8cfdf8c71a8ab76e5ec3bdd15638adf1f556add7657900639751043?color=5a5a5a)
Rechtsseitiger Grenzwert:
![\(\begin{array}[t]{rll}
&\lim\limits_{h\to 0\\h\gt 0}\dfrac{f(-2+h)-f(-2)}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0}\dfrac{-\dfrac{1}{2}(-2+h)^2+2-0}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0}\dfrac{-\dfrac{1}{2}(4-4h+h^2)+2}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0}\dfrac{-2+2h-\dfrac{h^2}{2}+2}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0}\dfrac{h\left(2-\dfrac{h}{2}\right)}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0} 2-\dfrac{h}{2} \\[5pt]
=& 2
\end{array}\)](https://mathjax.schullv.de/b511048497dbe91fb3118c88f3fc06b53d52a9d44ea0ffcaeeae3097218a0a25?color=5a5a5a)
Der rechts- und der linksseitige Grenzwert stimmen nicht überein. Daher ist die Funktion
Linksseitiger Grenzwert:
![\(\begin{array}[t]{rll}
&\lim\limits_{h\to 0\\h\lt 0}\dfrac{f(2+h)-f(2)}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0}\dfrac{-\dfrac{1}{2}(2+h)^2+2-0}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0}\dfrac{-\dfrac{1}{2}(4+4h+h^2)+2}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0}\dfrac{-2-2h-\dfrac{h^2}{2}+2}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0}\dfrac{h\left(-2-\dfrac{h}{2}\right)}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\lt 0} -2-\dfrac{h}{2} \\[5pt]
=& -2
\end{array}\)](https://mathjax.schullv.de/ffe0b06618e17ef02995eacb7377eb842b9ad24dfd43ff4c15309749908c33e2?color=5a5a5a)
Rechtsseitiger Grenzwert:
![\(\begin{array}[t]{rll}
&\lim\limits_{h\to 0\\h\gt 0}\dfrac{f(2+h)-f(2)}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0}\dfrac{\dfrac{1}{2}(2+h)^2-2-0}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0}\dfrac{\dfrac{1}{2}(4+4h+h^2)-2}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0}\dfrac{2+2h+\dfrac{h^2}{2}-2}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0}\dfrac{h\left(2+\dfrac{h}{2}\right)}{h} \\[5pt]
=& \lim\limits_{h\to 0\\h\gt 0} 2+\dfrac{h}{2} \\[5pt]
=& 2
\end{array}\)](https://mathjax.schullv.de/b28cc71be674f0c280ea467bffc81ac302e95f886c9bd60b043e3a2b5376a6f8?color=5a5a5a)
Der rechts- und der linksseitige Grenzwert stimmen nicht überein. Daher ist die Funktion