SchulLV Logo
Lerninhalte in Mathe
Digitales Schulbuch
Inhaltsverzeichnis

Verhalten für x → +∞ und x → -∞

Satz

Ist \(f: x\mapsto \dfrac{p(x)}{q(x)}\) eine gebrochen-rationale Funktion, wobei \(p(x)\) ein Polynom vom Grad \(z\) (Zählergrad) und \(q(x)\) ein Polynom vom Grad \(n\) (Nennergrad) ist, dann gilt für
  • \(\boldsymbol{z\lt n}:\) \(f\) konvergiert für \(x\rightarrow \infty\) und \(x\rightarrow -\infty\) gegen \(0\) und \(G_f\) hat die waagrechte Asymptote \(y=0.\)
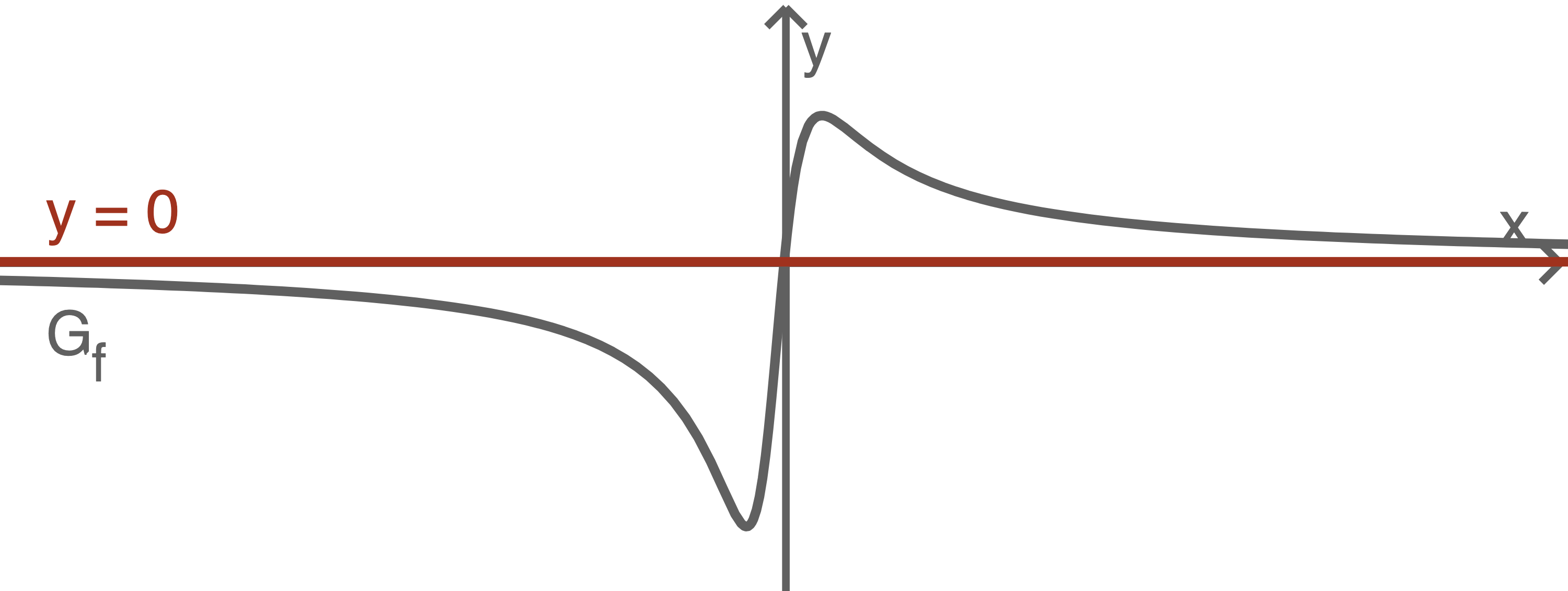
    gebrochen rationale funktionen, asymptote
  • \(\boldsymbol{z= n}:\) \(f\) konvergiert für \(x\rightarrow \infty\) und \(x\rightarrow -\infty\) gegen einen Wert \(c\in \mathbb R\backslash \{0\}\) und \(G_f\) hat die waagrechte Asymptote \(y=c.\)
    \(c\) lässt sich als Quotient der Leitkoeffizienten von \(p\) und \(q\) berechnen.
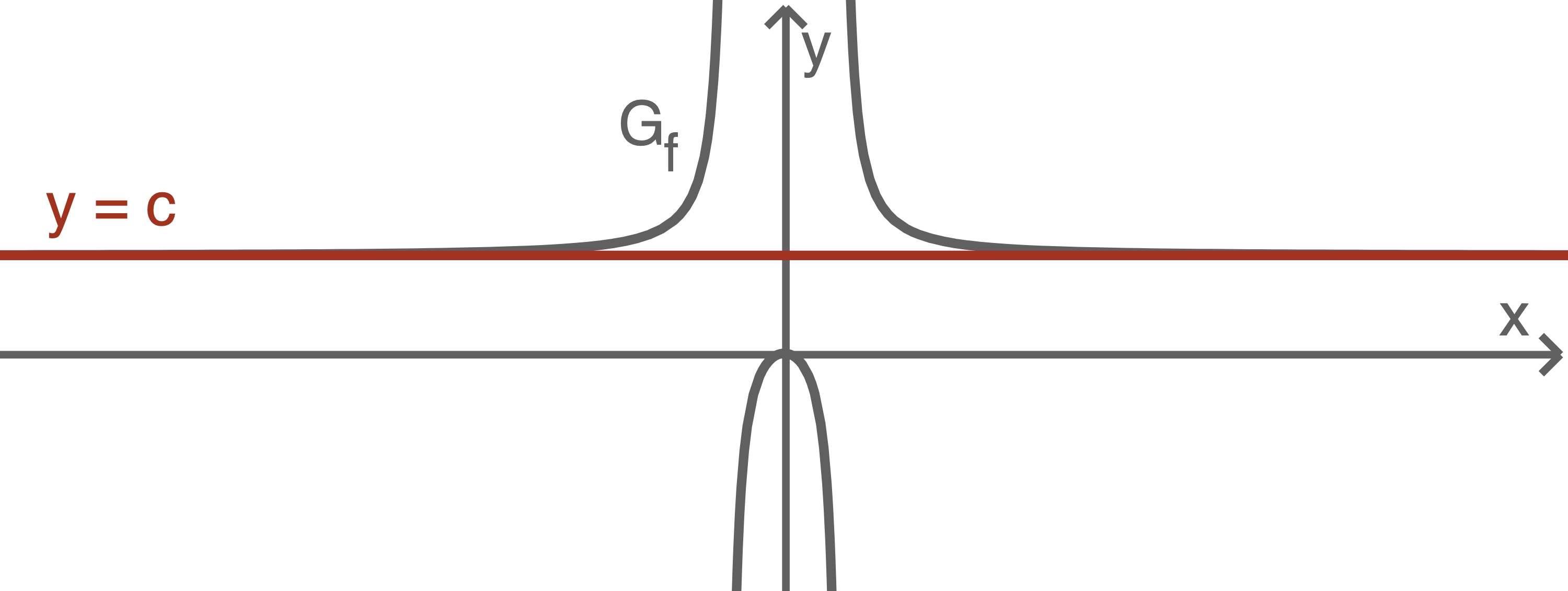
    gebrochen rationale funktionen, asymptote
  • \(\boldsymbol{z= n+1}:\) \(f\) divergiert für \(x\rightarrow \infty\) und \(x\rightarrow -\infty\) und \(G_f\) hat eine schräge Asymptote \(y=mx+c.\)
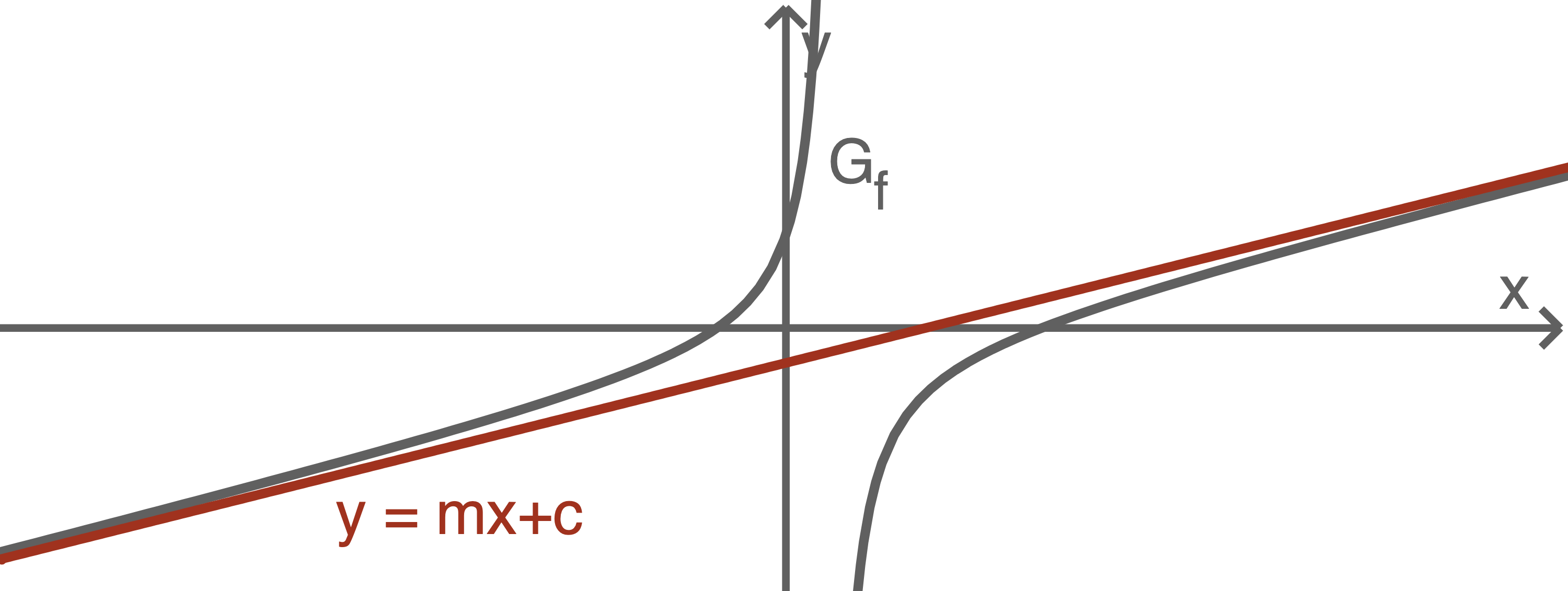
    gebrochen rationale funktionen, asymptote