Analytische Geometrie 3 - Körper

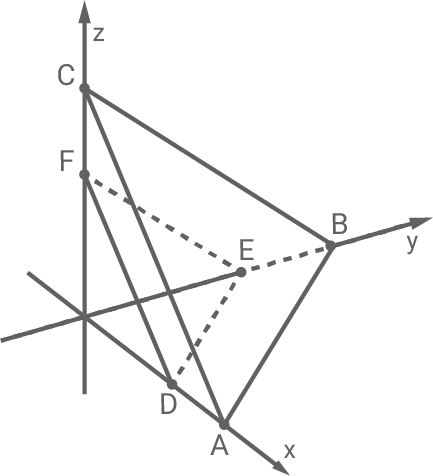
Die Abbildung zeigt den Körper $ABCDEF.$ Die Eckpunkte $A(4\mid0\mid 0),$ $B(0\mid4\mid 0)$ und $C(0\mid0\mid 4)$ liegen in der Ebene $L_1: x+y+z$ $=4,$ die Eckpunkte $D, E$ und $F$ jeweils auf einer Koordinatenachse und in der Ebene $L_2: 2x+2 y+2 z$ $=5.$

Prüfe, ob das Dreieck $ABC$ gleichseitig ist.
Bestimme die Koordinaten des Punkts $G$ auf der Seite $\overline{AC},$ für den $\vert\overline{AG}\vert:|\overline{GC}|$ $=1: 3$ gilt.

(4 BE)

Begründe, dass $L_1$ und $L_2$ keine gemeinsamen Punkte haben.

(2 BE)

Entscheide, ob der Abstand von $B$ und $E$ kleiner als der Abstand von $L_1$ und $L_2$ , größer als der Abstand von $L_1$ und $L_2$ oder genauso groß wie der Abstand von $L_1$ und $L_2$ ist. Begründe deine Entscheidung.

(3 BE)

Der Punkt $M(2\mid 2\mid 0)$ ist der Mittelpunkt der Strecke $\overline{AB}.$ Die Gerade durch den Punkt $P(0\mid 0\mid 2)$ und $M$ schneidet die Ebene $L_2$ in dem Punkt $Q.$
Ermittle die Koordinaten von $Q.$

(3 BE)

Bestimme die Größe des Winkels, den $L_2$ mit der $xy$ -Ebene einschließt.

(3 BE)

Die Oberfläche des Körpers $ABCDEF$ besteht aus zwei Dreiecken und drei Trapezen.
Begründe, dass der Punkt $T(1\mid 1\mid 1)$ im Inneren des Körpers $ABCDEF$ liegt.

(3 BE)

Ausgehend vom Ansatz $\frac{1}{3}$ $\cdot \frac{1}{2}$ $\cdot 4^2$ $\cdot 4$ $-\frac{1}{3}$ $\cdot \frac{1}{2}$ $\cdot k^2$ $\cdot k$ kann für einen Wert von $k \in \mathbb{R}$ das Volumen des Körpers $ABCDEF$ berechnet werden. Erläutere diesen Ansatz und bestimme den passenden Wert von $k.$

(4 BE)

Die folgenden Rechnungen liefern die Lösung einer Aufgabe im Zusammenhang mit dem Körper $ABCDEF:$

$\text{I}:$

$g: \vec{x}=\pmatrix{2,5\\0\\0}+t \cdot\pmatrix{1\\1\\0};\;t \in \mathbb{R}$

$\text{II}:$

$2,5+t+t=4 \Rightarrow t=0,75$ $\Rightarrow R(3,25\mid 0,75\mid 0)$

$\text{III}:$

$\sqrt{(2,5-3,25)^2+0,75^2} \approx 1,06$

Erläutere die einzelnen Schritte dieser Rechnung und gib an, welche geometrische Bedeutung das Ergebnis dieser Berechnung hat.

(4 BE)

Der Körper $ABCDEF$ wird so um seine Kante $\overline{AB}$ gedreht, dass der mit $C$ bezeichnete Eckpunkt des Körpers nach der Drehung in der $xy$ -Ebene liegt und dabei eine positive $x$ -Koordinate hat.
Berechne die Koordinaten dieses Eckpunkts nach der Drehung.

(4 BE)

(30 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\left\vert\overrightarrow{AB}\right\vert$ $= \left\vert\pmatrix{0\\4\\0}-\pmatrix{4\\0\\0}\right\vert$ $= \left\vert\pmatrix{-4\\4\\0}\right\vert$ $= \sqrt{32}$

$\left\vert\overrightarrow{BC}\right\vert$ $= \left\vert\pmatrix{0\\0\\4}-\pmatrix{0\\4\\0}\right\vert$ $= \left\vert\pmatrix{0\\-4\\4}\right\vert$ $= \sqrt{32}$

$\left\vert\overrightarrow{CA}\right\vert$ $= \left\vert\pmatrix{4\\0\\0}-\pmatrix{0\\0\\4}\right\vert$ $= \left\vert\pmatrix{4\\0\\-4}\right\vert$ $= \sqrt{32}$

Somit ist das Dreieck $ABC$ gleichseitig. Für den Punkt $G$ folgt:

$\overrightarrow{OG}$ $=\overrightarrow{OA}$ $+\dfrac{1}{4}\cdot \overrightarrow{AC}$ $=\pmatrix{3\\0\\1}$

Die Koordinaten des Punktes $G$ sind somit gegeben durch $G(3\mid0\mid1).$

$\overrightarrow{n}$ $= \pmatrix{1\\1\\1}$ ist ein Normalenvektor beider Ebenen. Die Abbildung zeigt, dass $L_1$ und $L_2$ nicht übereinstimmen, somit können sie keinen gemeinsamen Punkt haben.

Der Punkt $B$ liegt in $L_1$ und der Punkt $E$ liegt in $L_2.$ Da der Spurpunkt auf der $y$ -Achse liegt, folgt für die $y$ -Koordinate von $E:$

Rechenweg anzeigen

$y = \dfrac{5}{2}$

Somit hat $E$ die Koordinaten $E\left(0\mid\dfrac{5}{2}\mid0 \right).$ Da beide Ebenen denselben Normalenvektor besitzen, kann der Abstand der beiden Punkte somit nicht kleiner als der der beiden Ebenen sein. Die Punkte $B$ und $E$ liegen beide auf der Geraden mit Richtungsvektor $\pmatrix{0\\1\\0}.$

Dieser Vektor ist nicht kollinear zu $\overrightarrow{n},$ somit ist der Abstand der beiden Punkte größer als der der Ebenen.

1. Schritt: Geradengleichung aufstellen

$\overrightarrow{PM}$ $= \pmatrix{2\\2\\-2}$

$g:\overrightarrow{x}$ $=\pmatrix{0\\0\\2}+t\cdot\pmatrix{2\\2\\-2};\;t\in\mathbb{R}$

2. Schritt: Schnittpunkt berechnen

Einsetzen eines allgemeinen Punktes der Gerade $g$ in $L_2$ liefert:

$2\cdot2t$ $+2\cdot2t$ $+2\cdot(2-2t)$ $= 5$

Mit Hilfe des solve-Befehls des CAS folgt:

$t = \dfrac{1}{4}$

Einsetzen in die Geradengleichung liefert:

$\overrightarrow{OG}$ $= \pmatrix{0\\0\\2} + \dfrac{1}{4}\cdot \pmatrix{2\\2\\-2}$ $= \pmatrix{\frac{1}{2}\\\frac{1}{2}\\\frac{3}{2}}$

Die Koordinaten des Punktes $Q$ sind somit gegeben durch $Q\left(\frac{1}{2}\mid \frac{1}{2}\mid \frac{3}{2}\right).$

Aus der Winkelbeziehung zwischen zwei Ebenen folgt:

$\begin{array}[t]{rll} \cos(\alpha)&=&\dfrac{\vert\overrightarrow{n}\circ\overrightarrow{n_{xy}}\vert}{\vert\overrightarrow{n}\vert\cdot\vert\overrightarrow{n_{xy}}\vert} \\[5pt] \cos(\alpha)&=&\dfrac{\left\vert\pmatrix{1\\1\\1}\circ\pmatrix{0\\0\\1}\right\vert}{\left\vert\pmatrix{1\\1\\1}\right\vert\cdot\left\vert\pmatrix{0\\0\\1}\right\vert} \\[5pt] \end{array}$

Eingabe in den CAS liefert:

$\begin{array}[t]{rll} \alpha&\approx&55^\circ \end{array}$

Für eine Ebene $L_T,$ die parallel zu $L_1$ und $L_2$ liegt und den Punkt $T$ enthält, folgt mit Hilfe des gleichen Normalenvektors wie einem der anderen beiden Ebenen:

$L_T: x+y+z=d$

Einsetzen der Koordinaten von $T$ liefert:

$d$ $= 1+1+1$ $= 3$

Die Ebene kann somit durch $L_T: x+y+z=3$ beschrieben werden, das heißt $L_T$ verläuft oberhalb von $L_2: x+y+z=2,5$ und unterhalb von $L_1:x+y+z=4$ .

Weil $T$ auch nicht in einer der drei Koordinatenebenen liegt, muss $T$ damit im Inneren des Körpers liegen.

Der erste Summand gibt das Volumen der Pyramide $OABC$ an, der zweite das Volumen der Pyramide $ODEF$ .
Der Wert von $k$ stimmt mit der $x$ -Koordinate des Schnittpunkts von $L_2$ mit der $x$ -Achse überein. Einsetzen eines allgemeinen Punktes auf der $x$ -Achse in die Ebenengleichung von $L_2$ liefert:

Rechenweg anzeigen

$k=2,5$

Rechenschritte erläutern

$\text{I}:$

Die Gerade $g: \overrightarrow{x}=\pmatrix{2,5\\0\\0}+s \cdot\pmatrix{1\\1\\0}$ geht durch den Punkt $D,$ verläuft in der $xy$ -Ebene und schneidet die Strecke $\overline{AB}$ im rechten Winkel.

$\text{II}:$

Der Schnittpunkt $g$ mit der Ebene $L_1$ ist der Punkt $R$ mit den Koordinaten $R(3,25\mid0,75\mid0).$

$\text{III}:$

Der Abstand von $D$ zu $R$ beträgt ca. $1,06\;[\text{LE}].$

Geometrische Bedeutung angeben

Der ermittelte Wert $1,06\;[\text{LE}]$ gibt die Höhe des Trapezes $ABED$ an.

Die Strecke $\overline{MC}$ steht senkrecht auf der Strecke $\overline{AB}.$ Nach der Drehung liegt sie auf der Winkelhalbierenden der $xy$ -Ebene. Mit dem Mittelpunkt $M(2\mid 2\mid 0)$ von $\overline{AB}$ folgt für den Ortsvektor des Eckpunkts nach der Drehung:

Rechenweg anzeigen

$\( \overrightarrow{OC$

Die Koordinaten des Eckpunktes $C$ nach der Drehung sind somit gegeben durch $\(C$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?