Wahlaufgaben
1.4.1 Analysis
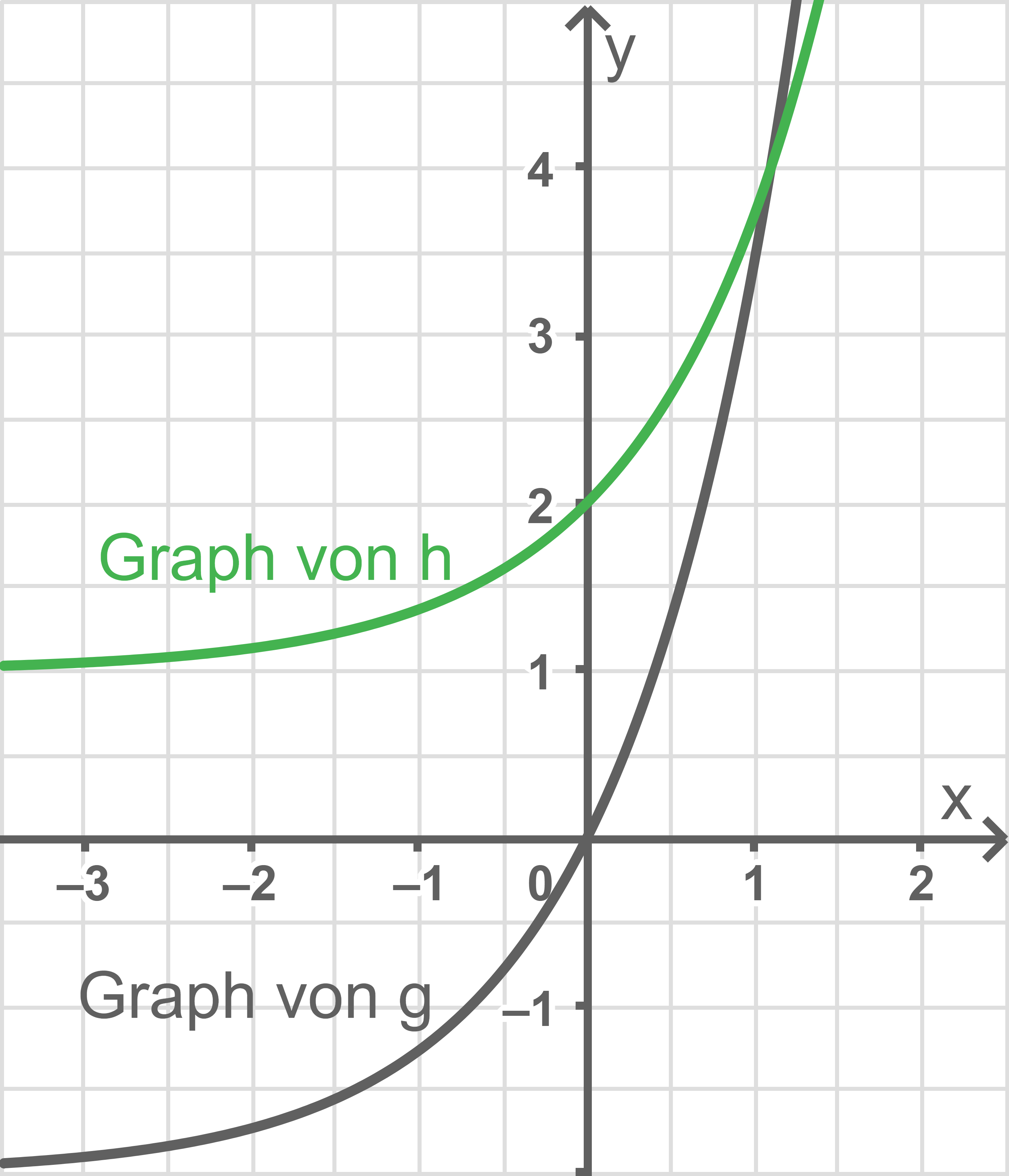
Gegeben sind die in  definierten Funktionen
definierten Funktionen  mit
mit  und
und  mit
mit  Die Abbildung zeigt ihre Graphen.
Die Abbildung zeigt ihre Graphen.

a)
Die erste Ableitungsfunktion von  wird mit
wird mit  bezeichnet.
bezeichnet.
Berechne und veranschauliche in der Abbildung, wie man diesen Wert grafisch ermitteln kann.
und veranschauliche in der Abbildung, wie man diesen Wert grafisch ermitteln kann.
Berechne
(3 BE)
b)
Beurteile die folgende Aussage:

Es gibt eine Verschiebung in  -Richtung, durch die der Graph von
-Richtung, durch die der Graph von  aus dem Graphen von
aus dem Graphen von  erzeugt werden kann.
erzeugt werden kann.
(2 BE)
1.4.2 Analytische Geometrie
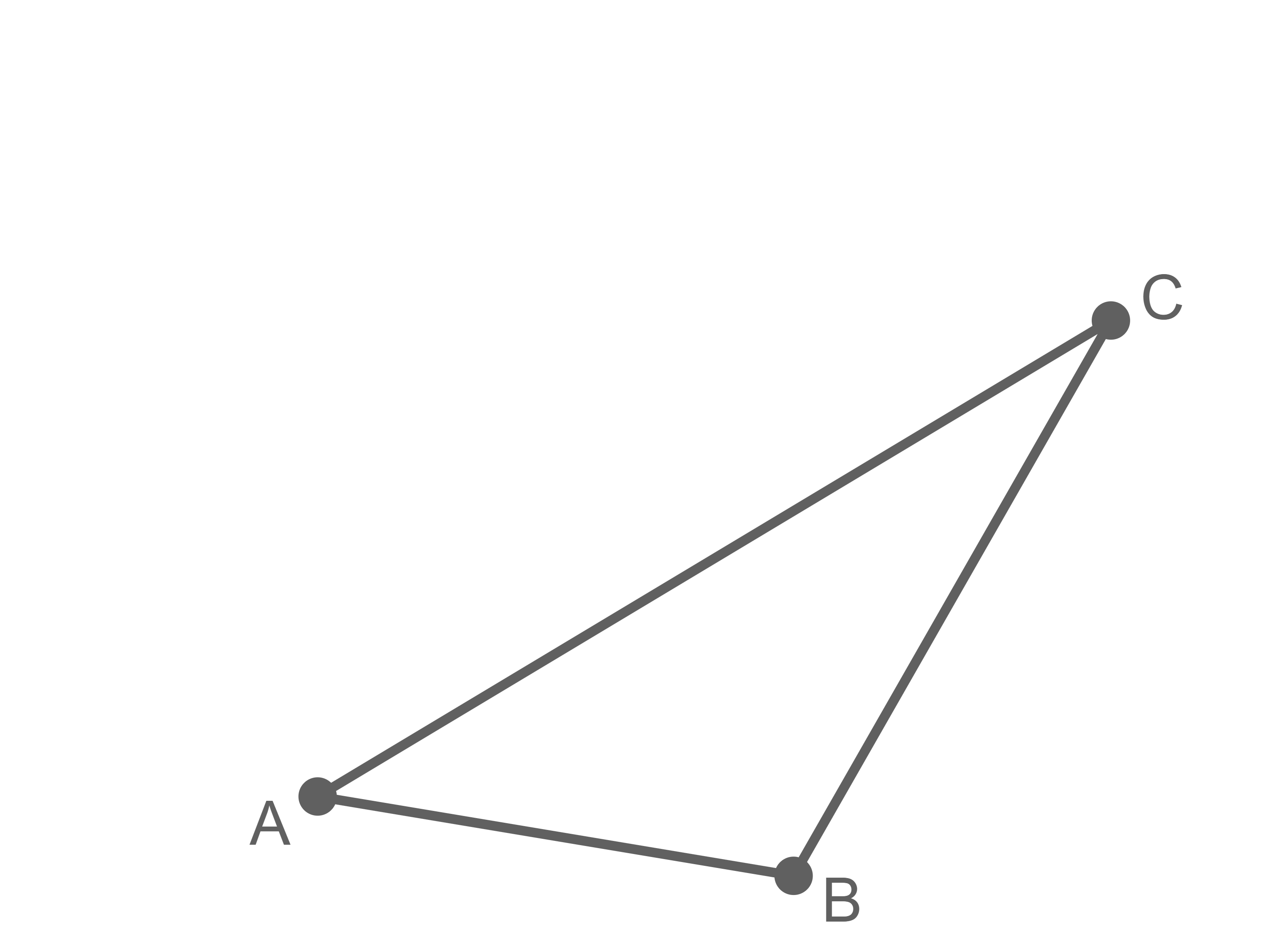
Gegeben ist das Dreieck  mit den Eckpunkten
mit den Eckpunkten  und
und  Für den Punkt
Für den Punkt  gilt
gilt  wobei
wobei  den Koordinatenursprung bezeichnet.
den Koordinatenursprung bezeichnet.
Ermittle das Verhältnis des Inhalts der Fläche des Dreiecks zum Inhalt der Fläche des Trapezes
zum Inhalt der Fläche des Trapezes 
Stelle dein Vorgehen durch eine geeignete Ergänzung der Abbildung dar.
Ermittle das Verhältnis des Inhalts der Fläche des Dreiecks
Stelle dein Vorgehen durch eine geeignete Ergänzung der Abbildung dar.
(5 BE)
1.4.3 Stochastik
In einem Spielwarengeschäft erhält jedes Kind im Rahmen einer Werbeaktion einen kleinen, blickdicht verpackten Ball. Die Wahrscheinlichkeit dafür, dass dieser Ball eine Glitzerfärbung hat, beträgt
a)
Zeige, dass die Wahrscheinlichkeit dafür, dass in einer Gruppe von drei Kindern jedes Kind einen Ball mit Glitzerfärbung erhält, kleiner als  ist.
ist.
(2 BE)
b)
Beschreibe im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term  berechnet werden kann. Gib dieses Ereignis an.
berechnet werden kann. Gib dieses Ereignis an.
(3 BE)
1.5.1 Analysis
Gegeben ist die in
a)
Weise nach, dass  streng monoton steigend verläuft.
streng monoton steigend verläuft.
(2 BE)
b)
Der Graph  wird so entlang der
wird so entlang der  -Achse verschoben, dass er durch den Koordinatenursprung verläuft. Es entsteht der Graph der Funktion
-Achse verschoben, dass er durch den Koordinatenursprung verläuft. Es entsteht der Graph der Funktion 
Ermittle eine Gleichung der Funktion
Ermittle eine Gleichung der Funktion
(3 BE)
1.5.2 Analytische Geometrie
Gegeben sind die Punkte
I.
II.
(5 BE)
1.5.3 Stochastik
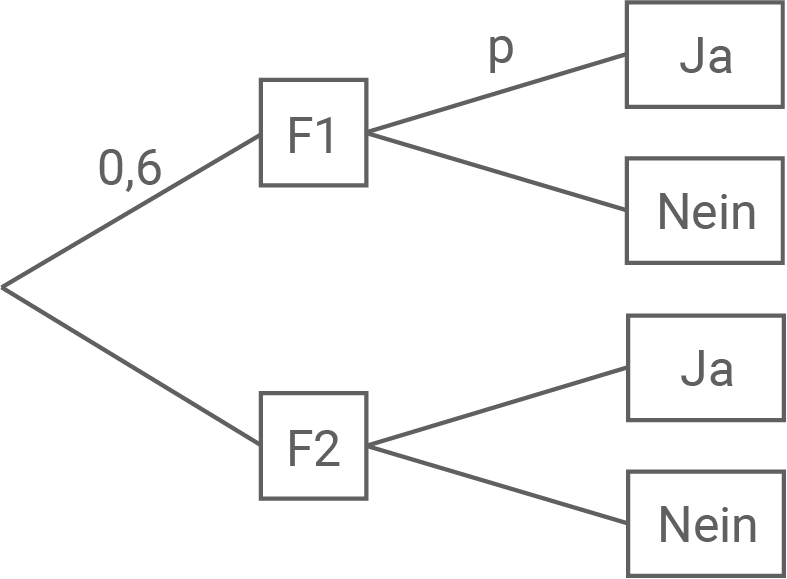
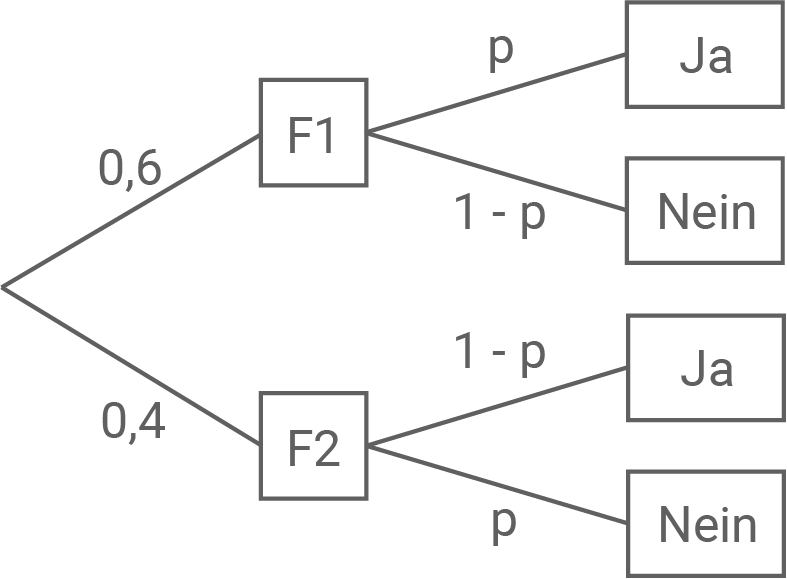
Um Jugendliche bei einer Befragung zum sensiblen Thema „Unentschuldigtes Fernbleiben vom Unterricht“ dazu zu bewegen, die ihnen gestellte Frage wahrheitsgemäß zu beantworten, wird folgendes Verfahren angewandt: Von den an der Befragung teilnehmenden Jugendlichen erhalten
F1:
„Ist es wahr, dass du schon einmal unentschuldigt dem Unterricht ferngeblieben bist?“
F2:
„Ist es wahr, dass du noch nie unentschuldigt dem Unterricht ferngeblieben bist?“
Nur der befragten Person selbst ist bekannt, welche der beiden Fragen sie erhalten hat. Sie beantwortet die Frage wahrheitsgemäß mit „Ja“ bzw. mit „Nein“.
Es kann davon ausgegangen werden, dass der Anteil der Befragten, die schon einmal unentschuldigt dem Unterricht ferngeblieben sind, unter denjenigen, die die Frage F1 erhielten, ebenso groß ist wie unter allen Befragten. Dieser Anteil wird mit
a)
Vervollständige das abgebildete Baumdiagramm, so dass es das beschriebene Verfahren darstellt.
(2 BE)
b)
Es werden 1000 Jugendliche befragt. Von diesen antworten 420 mit „Ja“.
Berechne den Anteil der sich auf Grundlage dieses Ergebnisses ergibt.
der sich auf Grundlage dieses Ergebnisses ergibt.
Berechne den Anteil
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?1.4.1 Analysis
a)
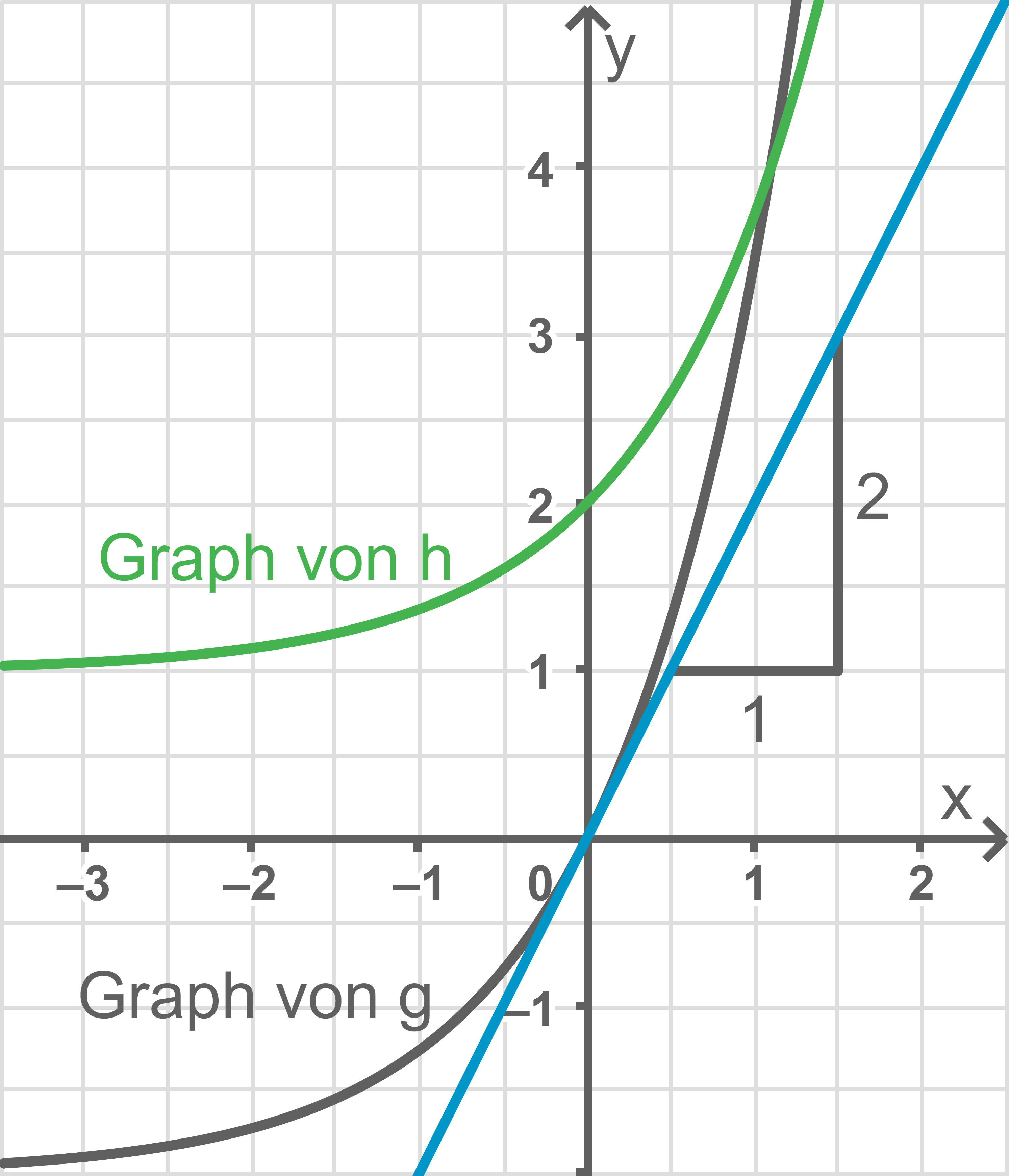
b)
Die Aussage ist falsch, da aus der Abbildung deutlich hervorgeht, dass die Steigung der beiden Graphen an der Stelle  nicht übereinstimmt.
nicht übereinstimmt.
1.4.2 Analytische Geometrie
Verhältnis der Flächeninhalte ermitteln
Der Flächeninhalt des Dreiecks  ergibt ergibt sich zu
ergibt ergibt sich zu  wobei
wobei  die Höhe von
die Höhe von  bezüglich der Seite
bezüglich der Seite  ist.
Da laut Aufgabenstellung
ist.
Da laut Aufgabenstellung  gilt, folgt
gilt, folgt  Für den Flächeninhalt des Trapezes gilt somit:
Für den Flächeninhalt des Trapezes gilt somit:
![\(\begin{array}[t]{rll}
A_{\text{Trapez}}&=&\dfrac{1}{2} \cdot\left(\left\vert\overline{AB}\right\vert+\left\vert\overline{CD}\right\vert\right) \cdot h \\[5pt]
&=&\dfrac{1}{2} \left(\left\vert\overline{AB}\right\vert+2\cdot\left\vert\overline{AB}\right\vert\right) \cdot h \\[5pt]
&=&\dfrac{3}{2} \cdot\left\vert\overline{AB}\right\vert \cdot h
\end{array}\)](https://mathjax.schullv.de/caae68f19a29e39be8efc1cd020a959cc01902d169860ea18a0bafabc9415750?color=5a5a5a) Damit ist das Verhältnis des Flächeninhalts des Dreiecks zu dem des Trapezes
Damit ist das Verhältnis des Flächeninhalts des Dreiecks zu dem des Trapezes  Vorgehen darstellen
Vorgehen darstellen
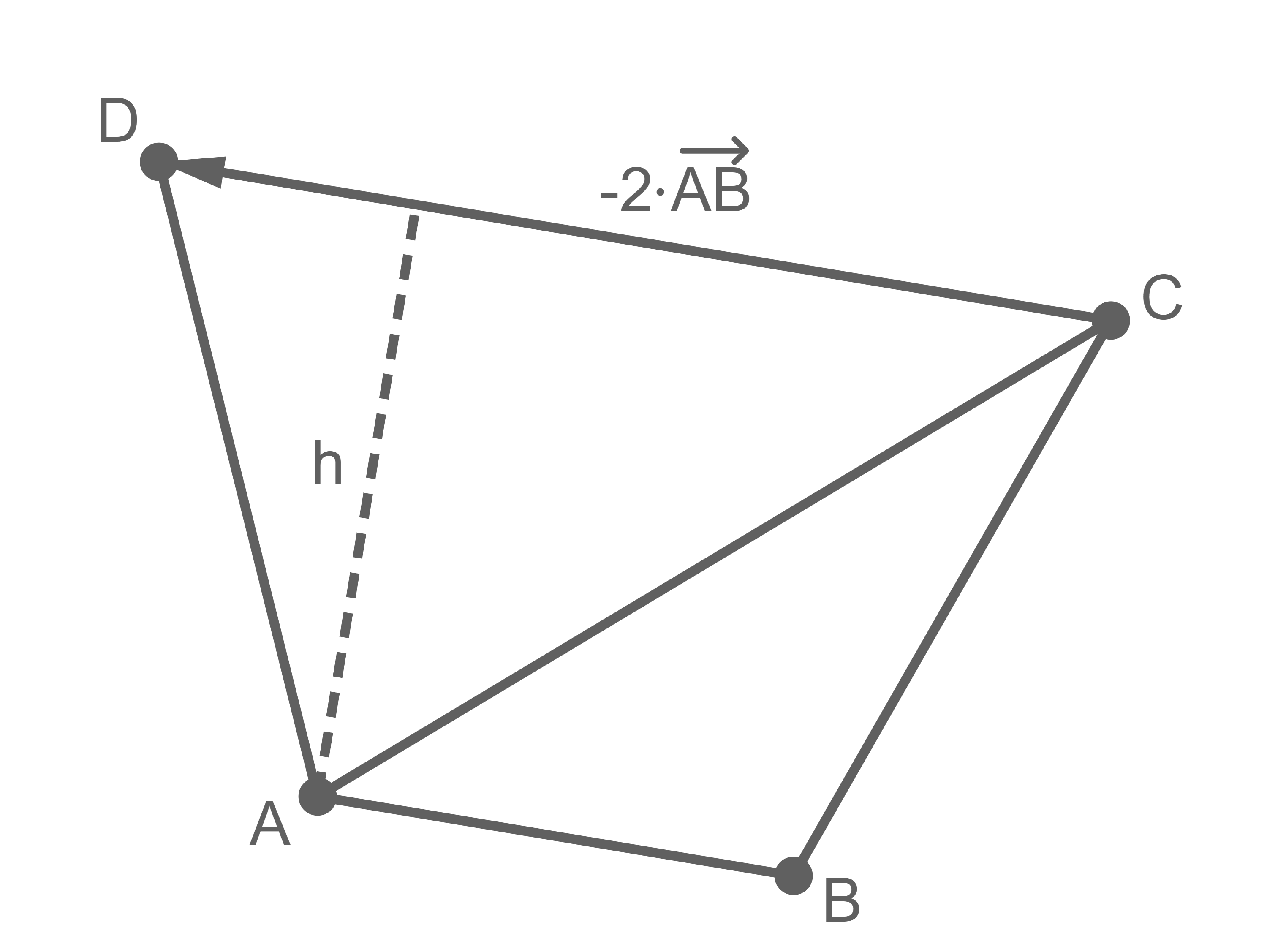

1.4.3 Stochastik
a)
b)
Ein mögliches Zufallsexperiment wäre, dass vier Kinder jeweils einen Ball bekommen. Das Ereignis, dessen Wahrscheinlichkeit durch den Term beschrieben wird, ist, dass mindestens drei von den vier Bällen keine Glitzerfärbung haben.
1.5.1 Analysis
a)
Für die Ableitung von  gilt:
gilt:
 Da stets
Da stets  gilt, folgt
gilt, folgt  und somit, dass
und somit, dass  streng monoton steigend verläuft.
streng monoton steigend verläuft.
b)
1.5.2 Analytische Geometrie
Die erste Bedingung liefert, dass die Punkte  und
und  auf einem Kreis mit Mittelpunkt
auf einem Kreis mit Mittelpunkt  liegen. Die zweite Bedingung wird zum Beispiel durch folgendes Dreieck erfüllt:
liegen. Die zweite Bedingung wird zum Beispiel durch folgendes Dreieck erfüllt:
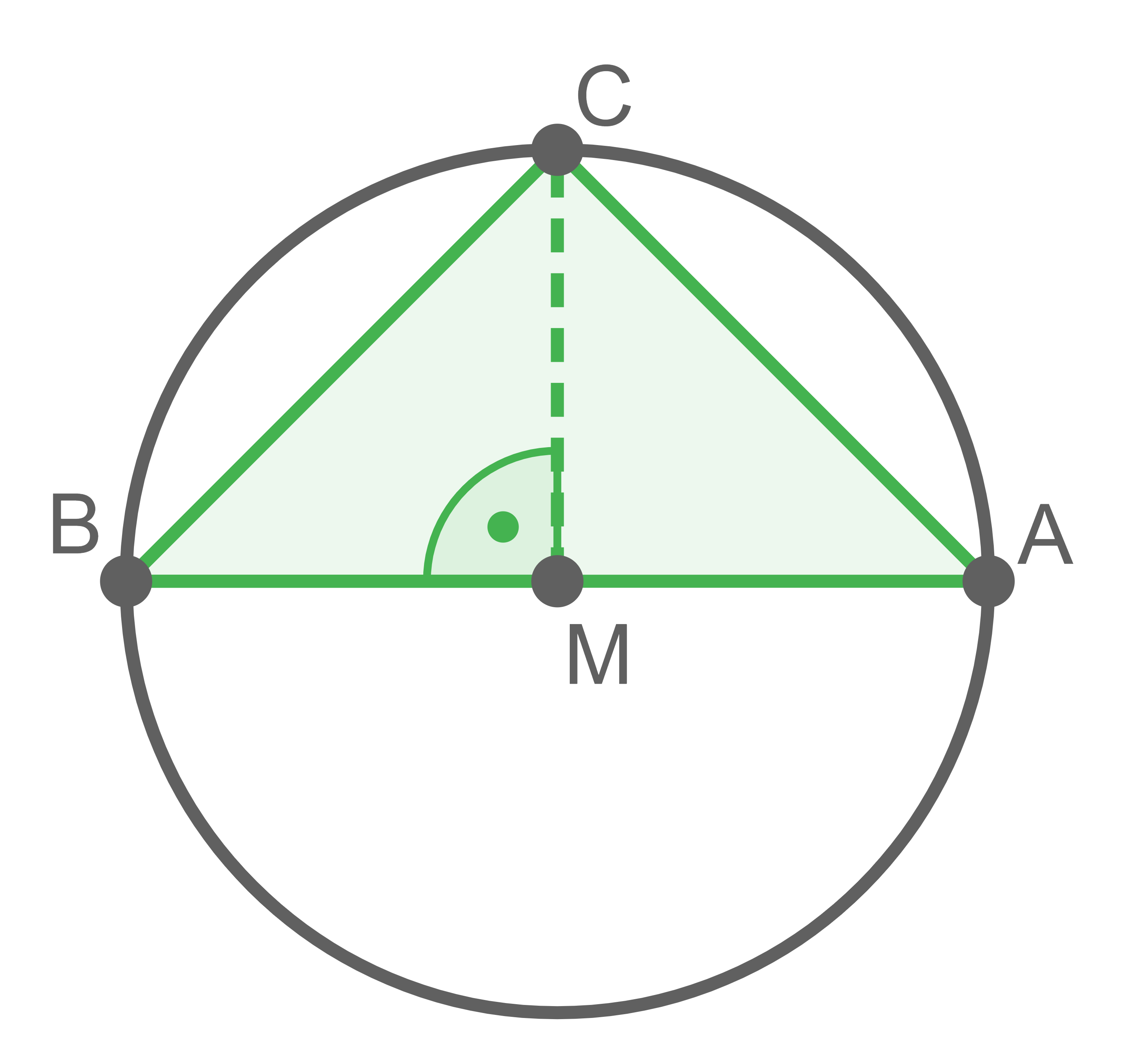 Für den Ortsvektor des Punkts
Für den Ortsvektor des Punkts  folgt somit:
folgt somit:
![\(\begin{array}[t]{rll}
\overrightarrow{OB}&=&\overrightarrow{OA}+2\cdot\overrightarrow{AM} \\[5pt]
&=&\pmatrix{3\\4\\0}+2\cdot\pmatrix{1-3\\2-4\\-1-0} \\[5pt]
&=&\pmatrix{-1\\0\\-2}
\end{array}\)](https://mathjax.schullv.de/ef0f3c39530411c85edbdf683f58fcc1f1821532ec15f22c8db129a3019981f6?color=5a5a5a) Ein Vektor
Ein Vektor  der senkrecht auf
der senkrecht auf  steht, das heißt für den
steht, das heißt für den  gilt, ist zum Beispiel gegeben durch:
gilt, ist zum Beispiel gegeben durch:
 Der Vektor
Der Vektor  muss nun ein Vielfaches dieses Vektors sein und den gleichen Betrag wie
muss nun ein Vielfaches dieses Vektors sein und den gleichen Betrag wie  besitzen. Somit folgt:
Die Koordinaten von zwei möglichen Punkten
besitzen. Somit folgt:
Die Koordinaten von zwei möglichen Punkten  und
und  die die beiden Bedingungen erfüllen, ergeben sich somit als
die die beiden Bedingungen erfüllen, ergeben sich somit als  und
und 

1.5.3 Stochastik
a)
b)