Analysis 2.2 - Bewässerungskanal
1
Gegeben sind die in  definierten Funktionen
definierten Funktionen  mit
mit 
 und
und  mit
mit  Die Graphen von
Die Graphen von  und
und  haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der
haben genau einen gemeinsamen Punkt; dieser Punkt liegt auf der  -Achse. Für die erste Ableitungsfunktion von
-Achse. Für die erste Ableitungsfunktion von  gilt
gilt 

a)
Beschreibe, wie der Graph von  aus dem Graphen von
aus dem Graphen von  erzeugt werden kann. Gib die Wertemenge von
erzeugt werden kann. Gib die Wertemenge von  an.
an.
(2 BE)
b)
Berechne die Größe des Winkels, in dem der Graph von  die Gerade mit der Gleichung
die Gerade mit der Gleichung  schneidet.
schneidet.
(3 BE)
c)
Zeige, dass die Graphen von  und
und  in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und gib eine Gleichung dieser Tangente an.
in ihrem gemeinsamen Punkt eine gemeinsame Tangente haben, und gib eine Gleichung dieser Tangente an.
(3 BE)
d)
Der Graph der Funktion  schließt mit der
schließt mit der  -Achse und der Geraden
-Achse und der Geraden  eine Fläche ein, von der ein Teil unterhalb der
eine Fläche ein, von der ein Teil unterhalb der  -Achse liegt. Berechne den Flächeninhalt.
-Achse liegt. Berechne den Flächeninhalt.
(4 BE)
e)
Gib die geometrische Bedeutung der Gleichung  an und bestimme den Wert von
an und bestimme den Wert von 
(3 BE)
2
Es ist eine in  definierte Funktion
definierte Funktion  mit
mit 

 gegeben.
gegeben.
a)
Berechne den Abstand der beiden Extrempunkte des Graphen von  Bestimme die Art dieser Extrempunkte.
Bestimme die Art dieser Extrempunkte.
(zur Kontrolle:  )
)
(6 BE)
b)
Es gibt genau eine Tangente an den Graphen von  die durch den Ursprung verläuft. Bestimme die Gleichung dieser Tangente und erläutere deine Rechnung.
die durch den Ursprung verläuft. Bestimme die Gleichung dieser Tangente und erläutere deine Rechnung.
(5 BE)
c)
Der Graph von  wird entlang der
wird entlang der  -Achse um
-Achse um  Einheiten so verschoben, dass der Mittelpunkt der Strecke zwischen den beiden Extrempunkten des verschobenen Graphen auf der
Einheiten so verschoben, dass der Mittelpunkt der Strecke zwischen den beiden Extrempunkten des verschobenen Graphen auf der  -Achse liegt.
-Achse liegt.
Bestimme den Wert des Parameters
Bestimme den Wert des Parameters
(4 BE)
3
Ein Bewässerungskanal wird durch Öffnen einer Schleuse in Betrieb genommen. Die in  definierte Funktion
definierte Funktion  mit
mit 

 beschreibt für
beschreibt für  die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle.
Dabei ist
die zeitliche Entwicklung der momentanen Durchflussrate des Wassers an einer Messstelle.
Dabei ist  die seit Beobachtungsbeginn vergangene Zeit in Sekunden und
die seit Beobachtungsbeginn vergangene Zeit in Sekunden und  die momentane Durchflussrate in Kubikmetern pro Sekunde. Die Abbildung zeigt den Graphen von
die momentane Durchflussrate in Kubikmetern pro Sekunde. Die Abbildung zeigt den Graphen von 
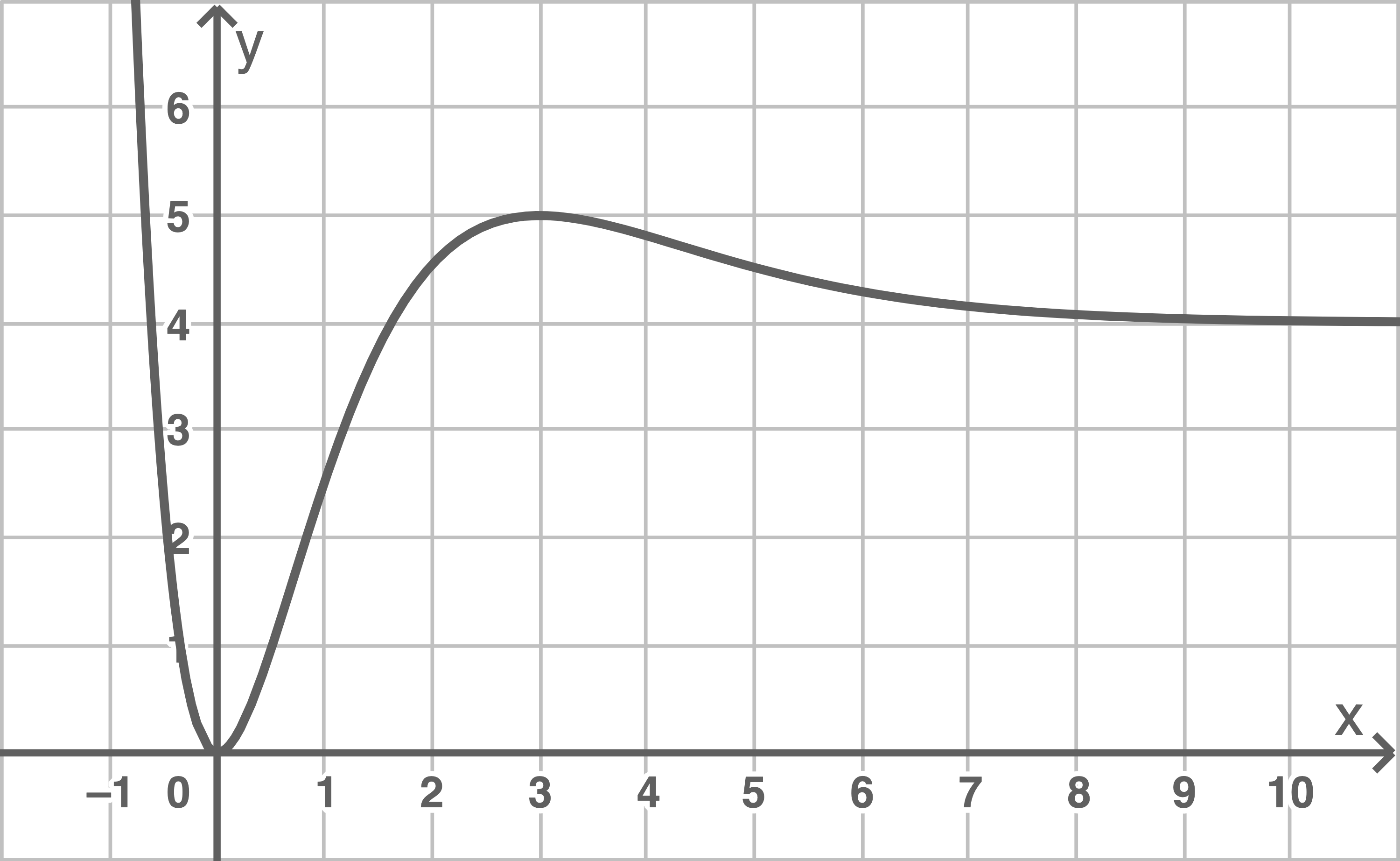
a)
Gib den Wert des Terms  sowie die Bedeutung dieses Werts im Sachzusammenhang an.
sowie die Bedeutung dieses Werts im Sachzusammenhang an.
(2 BE)
b)
Bestimme mithilfe der Abbildung die momentane Durchflussrate für denjenigen Zeitpunkt, zu dem sie am stärksten abnimmt.
(3 BE)
c)
Betrachtet wird der Zeitraum der ersten zehn Sekunden nach Beobachtungsbeginn. Beschreibe unter Verwendung geeigneter Flächen die graphische Bedeutung der folgenden Aussage:
 Für den betrachteten Zeitraum beträgt die mittlere Durchflussrate etwa
Für den betrachteten Zeitraum beträgt die mittlere Durchflussrate etwa 
(3 BE)
d)
Die Tangente an den Graphen von  im Punkt
im Punkt  wird durch die Gleichung
wird durch die Gleichung  dargestellt. Interpretiere die folgende Aussage im Sachzusammenhang:
dargestellt. Interpretiere die folgende Aussage im Sachzusammenhang:
 Für alle Werte von
Für alle Werte von  mit
mit  gilt
gilt 
(3 BE)
e)
An der Messstelle fließen in einem Zeitraum von drei Sekunden dreizehn Kubikmeter Wasser vorbei. Berechne die dafür infrage kommenden Zeiträume.
(4 BE)
(45 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Der Graph von  kann aus dem Graphen von
kann aus dem Graphen von  durch eine Spiegelung an der
durch eine Spiegelung an der  -Achse erzeugt werden.
Die Wertemenge ist somit als
-Achse erzeugt werden.
Die Wertemenge ist somit als ![\(]-\infty;0[\)](https://mathjax.schullv.de/888e03ff92be02be7bf4c1f6727dc815c2cf40ce5c08e62b2ad30aaa630e2f36?color=5a5a5a) gegeben.
gegeben.
b)
Im Schnittpunkt gilt  somit gilt dort also
somit gilt dort also  Mit der Formel für den Steigungswinkel folgt:
Mit der Formel für den Steigungswinkel folgt:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&-4 \\[5pt]
\alpha&\approx&-76^\circ
\end{array}\)](https://mathjax.schullv.de/79a5ae4ebc50eb6b4025fd45017e122c8abd9cc341247b1ad88d53223d4d190c?color=5a5a5a) Die Größe des Schnittwinkels beträgt somit ca.
Die Größe des Schnittwinkels beträgt somit ca. 
c)
1. Schritt: Koordinaten des gemeinsamen Punktes ermitteln
 und
und  gleichsetzen:
gleichsetzen:
 Mit dem CAS ergibt sich
Mit dem CAS ergibt sich  als Lösung der Gleichung, womit die Koordinaten des gemeinsamen Punktes mit
als Lösung der Gleichung, womit die Koordinaten des gemeinsamen Punktes mit  folgen.
2. Schritt: Nachweis der gemeinsamen Tangente
Damit die beiden Graphen an dieser Stelle eine gemeinsame Tangente haben, muss ebenfalls die Steigung übereinstimmen.
Die Ableitungsfunktionen lauten:
folgen.
2. Schritt: Nachweis der gemeinsamen Tangente
Damit die beiden Graphen an dieser Stelle eine gemeinsame Tangente haben, muss ebenfalls die Steigung übereinstimmen.
Die Ableitungsfunktionen lauten:

 Mit
Mit  und
und  liegt in
liegt in  eine gemeinsame Tangente vor.
3. Schritt: Gleichung der gemeinsamen Tangente angeben
Für die Steigung der Tangente gilt
eine gemeinsame Tangente vor.
3. Schritt: Gleichung der gemeinsamen Tangente angeben
Für die Steigung der Tangente gilt  Da
Da  auf der
auf der  -Achse liegt, folgt
-Achse liegt, folgt  Die Gleichung der Tangente lautet somit mit
Die Gleichung der Tangente lautet somit mit 
d)
1. Schritt: Nullstellen von  berechnen
berechnen
 wird mit dem CAS gelöst:
wird mit dem CAS gelöst:
![\(\begin{array}[t]{rll}
x_1&=&\dfrac{-1+\sqrt{5}}{2} \\[5pt]
x_2&=&\dfrac{-1-\sqrt{5}}{2}
\end{array}\)](https://mathjax.schullv.de/2ad899b1e6d72a6e7a213863f0bee397fce903a34b49d6229e4e2a207e4fc162?color=5a5a5a) 2. Schritt: Inhalt des Flächenstücks berechnen
Beim Graphen von
2. Schritt: Inhalt des Flächenstücks berechnen
Beim Graphen von  handelt es sich um eine Parabel, deren Tiefpunkt unterhalb der
handelt es sich um eine Parabel, deren Tiefpunkt unterhalb der  -Achse liegt.
Somit ergibt sich der gesuchte Flächeninhalt mittels CAS:
-Achse liegt.
Somit ergibt sich der gesuchte Flächeninhalt mittels CAS:



![\( = \dfrac{1}{4}\cdot(5\sqrt{5}-3)\;[\text{FE}]\)](https://mathjax.schullv.de/2222f1061188676ff98011d50b85446d2d459969b56abe1bb35e85ef4b0434d7?color=5a5a5a)
e)
Geometrische Bedeutung angeben
Die Fläche, die die Graphen von  und
und  und die Gerade mit der Gleichung
und die Gerade mit der Gleichung  einschließen, hat den Inhalt
einschließen, hat den Inhalt  Wert von
Wert von  bestimmen
bestimmen




 Mit Hilfe des solve-Befehls des CAS folgt:
Mit Hilfe des solve-Befehls des CAS folgt:

2
a)
Zweimaliges Ableiten von  im CAS liefert:
im CAS liefert:





 Abstand der Extrempunkte berechnen
Notwendige Bedingung für Extremstellen anwenden:
Abstand der Extrempunkte berechnen
Notwendige Bedingung für Extremstellen anwenden:
 Mit Hilfe des solve-Befehls des CAS ergeben sich
Mit Hilfe des solve-Befehls des CAS ergeben sich  und
und  (Auf die Anwendung der hinreichenden Bedingung für Extremstellen wird verzichtet, da die Aufgabenstellung fordert, dass es sich um Extrempunkte handelt.)
Einsetzen in
(Auf die Anwendung der hinreichenden Bedingung für Extremstellen wird verzichtet, da die Aufgabenstellung fordert, dass es sich um Extrempunkte handelt.)
Einsetzen in  liefert die
liefert die  -Koordinaten der Extrempunkte:
-Koordinaten der Extrempunkte:
![\(\begin{array}[t]{rll}
v(0)&=&4\cdot(0^2-0-1)\cdot \mathrm e^{-0} \\[5pt]
&=&-4
\end{array}\)](https://mathjax.schullv.de/cf797752ac04a006f4a4534be577c4d59d201a0fa12ee836831fd2d7a1b6b6a3?color=5a5a5a)
![\(\begin{array}[t]{rll}
v(3)&=&4\cdot(3^2-3-1)\cdot \mathrm e^{-3} \\[5pt]
&=&20\cdot\mathrm e^{-3}
\end{array}\)](https://mathjax.schullv.de/d8f92eae6972e350e9843a2110483a355701f852b5c1ea480e43e2e5d35ae703?color=5a5a5a) Für den Abstand beider Extrempunkte folgt somit:
Für den Abstand beider Extrempunkte folgt somit:


![\( \approx 5,83\;[\text{LE}] \)](https://mathjax.schullv.de/b8bb5c5e993ad55cf9086706cea0f6a418ae7337800020552754f695bf6e8213?color=5a5a5a) Art der Extrempunkte bestimmen
Art der Extrempunkte bestimmen
![\(\begin{array}[t]{rll}
v](https://mathjax.schullv.de/b4f10655011864e711a77f13b9e0eeb7497132cbfee6a8a4d5064e0cdbe8cda5?color=5a5a5a)
![\(\begin{array}[t]{rll}
v](https://mathjax.schullv.de/6ea2fc6c1d5c2a78f1f9bd81ec6cc97ea14af28edd681e3fd2169543621bafdb?color=5a5a5a) Der Graph der Funktion
Der Graph der Funktion  hat somit einen Tiefpunkt mit den Koordinaten
hat somit einen Tiefpunkt mit den Koordinaten  und einen Hochpunkt mit den Koordinaten
und einen Hochpunkt mit den Koordinaten 
b)
Die Tangente soll  erfüllen, somit folgt die Tangentengleichung mit
erfüllen, somit folgt die Tangentengleichung mit  Für die Steigung gilt:
Für die Steigung gilt: 

 Im Berührpunkt der Tangente an den Graphen von
Im Berührpunkt der Tangente an den Graphen von  gilt
gilt  das heißt:
das heißt:



 Mit Hilfe des solve-Befehls des CAS folgt:
Mit Hilfe des solve-Befehls des CAS folgt:  Einsetzen in
Einsetzen in 

 ergibt:
ergibt:



 Die Gleichung der gesuchten Tangente ist somit durch
Die Gleichung der gesuchten Tangente ist somit durch  gegeben.
gegeben.
c)
3
a)
Ablesen aus Abbildung 2: Es ist  Im Sachzusammenhang bedeutet dies, dass sich die momentane Durchflussrate langfristig einem Wert von
Im Sachzusammenhang bedeutet dies, dass sich die momentane Durchflussrate langfristig einem Wert von  annähert.
annähert.
b)
Die stärkste Abnahme liegt an derjenigen Wendestelle  des Graphen von
des Graphen von  vor, für die
vor, für die  gilt.
Der Wendepunkt im betrachteten Zeitraum, wird aus der Abbildung abgelsen und hat circa die Koordinaten
gilt.
Der Wendepunkt im betrachteten Zeitraum, wird aus der Abbildung abgelsen und hat circa die Koordinaten  Damit beträgt die momentane Durchflussrate zum betrachteten Zeitpunkt etwa
Damit beträgt die momentane Durchflussrate zum betrachteten Zeitpunkt etwa  .
.
c)
Das Flächenstück, das der Graph von  zwischen
zwischen  mit der
mit der  -Achse einschließt, hat etwa den gleichen Inhalt wie das Flächenstück, welches die Gerade mit der Gleichung
-Achse einschließt, hat etwa den gleichen Inhalt wie das Flächenstück, welches die Gerade mit der Gleichung  und die
und die  -Achse für
-Achse für  einschließen.
einschließen.
d)
Für den angegebenen Zeitraum beschreibt die Tangente die zeitliche Entwicklung der momentanen Durchflussrate mit einer relativen Abweichung von weniger als 
e)