Analysis 2.1 - Schrankknauf

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=(x-2) \cdot \mathrm e^{-\frac{1}{2} x+3}.$ Der Graph von $f$ wird mit $G_f$ bezeichnet.

Die Funktion $f$ hat genau eine Nullstelle. Gib diese an.
Ermittle die Koordinaten des Schnittpunktes des Graphen $G_f$ mit der $y$ -Achse.

(2 BE)

Der Graph $G_f$ hat genau einen Hochpunkt.
Bestimme rechnerisch die Koordinaten des Hochpunkts von $G_f.$

(zur Kontrolle: Hochpunkt $(4 \mid f(4))$ )

(3 BE)

Der Graph $G_f$ hat einen Wendepunkt.
Begründe anhand des Funktionsterms der zweiten Ableitungsfunktion von $f,$ dass $G_f$ genau einen Wendepunkt hat.
Weise nach, dass der Punkt $(6 \mid 4)$ der Wendepunkt von $G_f$ ist.

(3 BE)

Entscheide für jede der Aussagen I und II, ob sie richtig oder falsch ist.
Begründe deine Entscheidung.

Die Gerade durch die Punkte $A(2 \mid 0)$ und $B(6 \mid f(6))$ ist senkrecht zu der Tangente an den Graphen von $f,$ die am stärksten fällt.

Es gibt genau ein rechtwinkliges Dreieck $ADC$ mit den folgenden Eigenschaften.

Die Punkte $A(2 \mid 0), C(3 \mid f(3))$ und $D$ liegen auf dem Graphen $G_f.$
$\overline{AD}$ ist die Hypotenuse des Dreiecks $ADC.$

(6 BE)

Die drei folgenden Rechenschritte liefern die Lösung einer Aufgabe:

$d(x)=\sqrt{(x-2)^2+(f(x)-0)^2}$
$d(x)=20 \Rightarrow x_1 \approx 22 ; x_2 \approx 0,6$ (entfällt)
$f(22) \approx 0,007$

Formuliere eine zugehörige Aufgabenstellung und erläutere den dargestellten Lösungsweg.

(3 BE)

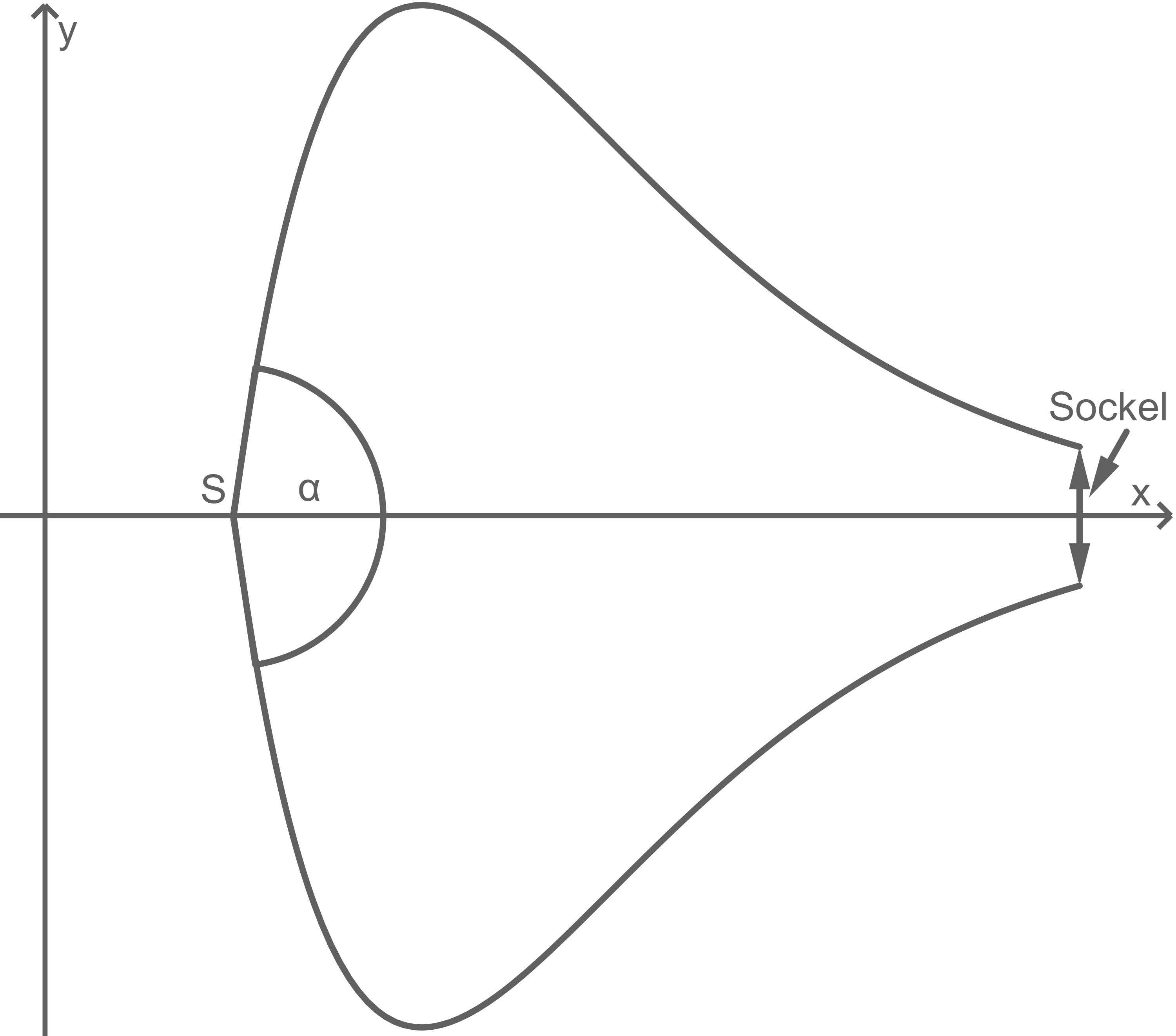
Die Form eines Schrankknaufs kann beschrieben werden als Körper, der durch Rotation von $G_f$ um die $x$ -Achse entsteht. In der Abbildung 1 wird die Querschnittsfläche eines Schrankknaufs dargestellt. Ein Teil der Profillinien des Querschnitts wird für $2 \leq x \leq 11$ modellhaft durch die Graphen der Funktionen $f$ und $g$ beschrieben, wobei der Graph von $g$ durch Spiegelung des Graphen von $f$ an der $x$ -Achse entsteht. Es gilt: $1\;\mathrm{LE}=0,5\;\mathrm{cm}.$

Abb. 1

Gib eine Funktionsgleichung von $g$ an.
Bestimme den Durchmesser des Sockels des Schrankknaufs in $\text{mm}.$

(3 BE)

Der Schrankknauf soll aus einem Holzquader gefertigt werden. Ein Kubikzentimeter der verwendeten Holzart hat eine Masse von $0,86\;\text{g}.$
Gib die Maße an, die dieser Holzquader mindestens haben muss.
Berechne die Masse des Holzquaders.

(4 BE)

Eine Vorgabe für den Schrankknauf ist die Größe des Winkels $\alpha$ an der Spitze $S.$ Er sollte mindestens $160^{\circ}$ betragen.
Prüfe rechnerisch, ob die Vorgabe eingehalten wird.

(3 BE)

Bestimme die Größe der Querschnittsfläche eines Schrankknaufs in $\text{cm}^2.$

(3 BE)

Die obere Profillinie eines weiteren Schrankknaufs soll durch den Graphen einer ganzrationalen Funktion $p$ dritten Grades mit folgenden Eigenschaften beschrieben werden

der Graph von $p$ hat mit der $x$ -Achse nur den Punkt $N(2 \mid 0)$ gemeinsam;
der Anstieg der Tangente an den Graphen von $p$ im Punkt $M(3 \mid p(3))$ ist $2;$
der Punkt $H(5 \mid p(5))$ ist der Extrempunkt des Graphen von $p;$
die Größe der Fläche zwischen dem Graphen von $p$ und der $x$ -Achse im Intervall $[2; 8]$ beträgt $20.$

Gib Gleichungen an, mit deren Hilfe die Funktionsgleichung $p$ ermittelt werden kann.

(5 BE)

(35 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Nullstelle angeben

Da die $\mathrm e$ -Funktion keine Nullstellen besitzt, folgt aus dem Funktionsterm von $f$ die Stelle $x=2$ als Nullstelle von $f.$

Koordinaten ermitteln

$\begin{array}[t]{rll} f(0)&=&(0-2)\cdot\mathrm e^{-\frac{1}{2}\cdot0+3} \\[5pt] &=&-2\mathrm e^{3} \end{array}$

Die Koordinaten des gesuchten Schnittpunkts des Graphen $G_f$ mit der $y$ -Achse ergeben sich somit als $S(0\mid-2\mathrm e^3).$

Ableiten von $f$ im CAS liefert:

$\(f$

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(f$

Mit dem solve-Befehl des CAS folgt:

$x=4$

Da $G_f$ laut Aufgabenstellung genau einen Hochpunkt besitzt, muss die hinreichende Bedingung nicht überprüft werden.

2. Schritt: Koordinaten bestimmen

$f(4)=(4-2) \cdot \mathrm e^{-\frac{1}{2}\cdot4+3}=2\mathrm e$

Die Koordinaten des Hochpunkts von $G_f$ sind somit durch $H(4\mid2\mathrm e)$ gegeben.

Begründen, dass $\boldsymbol{G_f}$ genau einen Wendepunkt hat

Mit dem CAS folgt für $\(f$

$\(f$

Da die $\mathrm e$ -Funktion stets ungleich null ist, gilt $\(f$ nach dem Satz des Nullprodukts genau dann, wenn $\frac{1}{4} x-\frac{3}{2}=0$ gilt. Diese Gleichung hat genau eine Nullstelle, das heißt nach dem notwendigen Kriterium für Wendestellen kann $G_f$ nicht mehr als einen Wendepunkt besitzen und hat somit mit Hilfe der Aufgabenstellung genau einen Wendepunkt.

Notwendige Bedingung für Wendestellen überprüfen

$\(\begin{array}[t]{rll} f$

Der Wendepunkt des Graphen $G_f$ ist somit an der Stelle $x=6.$ Für die $y$ -Koordinate folgt:

$\begin{array}[t]{rll} f(6)&=&(6-2) \cdot \mathrm e^{-\frac{1}{2} \cdot 6+3} \\[5pt] &=&4 \end{array}$

Damit ist der Punkt $(6\mid4)$ der Wendepunkt von $G_f.$

Aussage I

Die Tangente an den Graphen von $f,$ die am stärksten fällt, ist die Tangente im Wendepunkt von $G_f.$ Für die Steigung dieser gilt:

$\(f$

Für die Steigung $m$ der Gerade aus der Aussage folgt:

$m=\dfrac{f(6)-0}{6-2}=\dfrac{4}{4}=1$

Da $\(m\cdot f$ gilt, stehen die beiden Geraden senkrecht aufeinander und die Aussage ist wahr.

Aussage II

Die zweite Eigenschaft besagt, dass der rechte Winkel des Dreiecks im Punkt $C$ liegt.
Darstellung der Geraden durch $A$ und $C$ im CAS und der Geraden, die zu dieser senkrecht und durch den Punkt $C$ verläuft, zeigt, dass letztere den Graphen von $f$ in zwei Punkten schneidet. Somit existieren zwei geeignete Punkte $D$ und damit zwei rechtwinklige Dreiecke $ADC,$ die die Bedingungen erfüllen. Aussage II ist somit falsch.

Aufgabenstellung formulieren

„Berechne die Koordinaten des Punktes auf dem Graphen von $f,$ der zum Punkt mit den Koordinaten $(2 \mid 0)$ einen Abstand von $20\;\text{LE}$ hat und im I. Quadranten liegt.“

Lösungsweg erläutern

Der erste Schritt liefert die Funktion, die den Abstand des Punktes $(x\mid f(x))$ zu dem Punkt mit den Koordinaten $(2\mid0)$ angibt.
Der zweite Schritt liefert die Stellen $x,$ für die der zugehörige Abstand $20\;\text{LE}$ beträgt.
Im letzten Schritt wird durch Einsetzen des Wertes von $x$ in $f(x)$ der zugehörige Funktionswert des Punktes bestimmt.

Funktionsgleichung von $\boldsymbol{g}$ angeben

$g(x)=-f(x)=-(x-2) \cdot \mathrm e^{-\frac{1}{2} x+3}$

Durchmesser bestimmen

$\begin{array}[t]{rll} f(11)&=&(11-2) \cdot \mathrm e^{-\frac{1}{2}\cdot11+3} \\[5pt] &\approx&0,74 \end{array}$

Für den Durchmesser $d$ des Sockels folgt somit $d=2\cdot0,74=1,48\;[\text{LE}].$ Da $1\;\text{LE}=0,5\;\text{cm}=5\;\text{mm}$ gilt, folgt somit, dass der Durchmesser des Sockels $d=1,48\cdot5\approx7\;[\text{mm}]$ beträgt.

Maße des Holzquaders angeben

Nach Aufgabenteil b) ist die $y$ -Koordinate des Hochpunkts von $f$ gegeben durch $y=2\mathrm e.$ Die Tiefe und Höhe des Quaders muss somit jweils $2\mathrm e \cdot 2\cdot 0,5=2\mathrm e\;[\text{cm}]$ betragen.

Da der Querschnitt zwischen $x=2$ und $x=11$ liegt, folgt für die benötigte Breite des Quaders $(11-2)\cdot0,5=4,5\;[\text{cm}].$

Masse des Holzquaders berechnen

Für das Volumen $V$ des Holzquaders folgt:

$V=4,5\cdot2\mathrm e\cdot2\mathrm e\approx133\;[\text{cm}^3]$

Damit folgt für die Masse $m=0,86\cdot V\approx114,38\;[\text{g}].$

Der Winkel $\alpha$ setzt sich aus den beiden gleich großen Schnittwinkeln von $f$ und $g$ mit der $x$ -Achse zusammen. Somit folgt:

$\(\begin{array}[t]{rll} \dfrac{\alpha}{2}&=&\tan^{-1}(f$

Die Vorgabe wird somit eingehalten.

Rechenweg anzeigen

$A \approx 55,5\;[\text{FE}]$

Die Größe der Querschnittsfläche eines Schrankknaufs in $\text{cm}^2$ beträgt somit ca. $55,5\cdot0,5^2\approx13,89\;[\text{cm}^2].$

Für die allgemeine Form von $p$ und der ersten Ableitung folgt:

$p(x)=ax^3+bx^2+cx+d$

$\(p$

Die Eingeschaften aus der Aufgabenstellung liefern somit folgende Gleichungen, mit denen sich durch Einsetzen der allgemeinen Funktionsterme von $p$ und $\(p$ die Werte $a,b,c$ und $d$ ergeben:

$p(2)=0$
$\(p$
$\(p$
$20=\displaystyle\int_{2}^{8}p(x)\;\mathrm dx$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?