Hilfsmittelfreier Teil
1.1 Analysis
Eine Funktion
a)
Berechne die Nullstellen der Funktion  .
.
(2 BE)
b)
Bestimme die Gleichung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  .
.
(3 BE)
1.2 Analysis
Abgebildet ist der Graph einer Funktion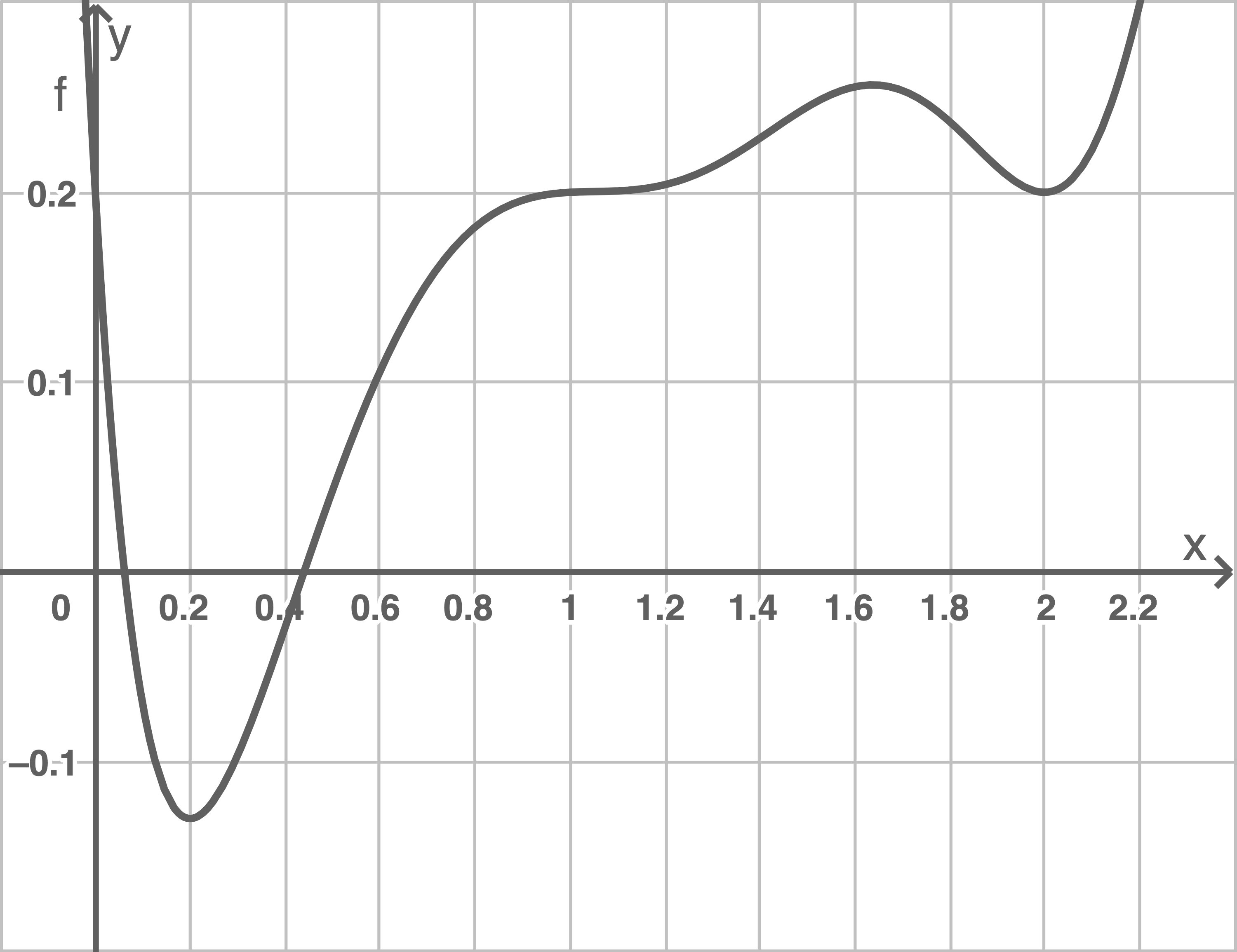
a)
Gib je einen Wert für  und
und  an, so dass gilt:
an, so dass gilt:
(2 BE)
b)
Markiere einen Punkt  auf dem Funktionsgraphen von
auf dem Funktionsgraphen von  , für den gilt:
, für den gilt:
 und
und  .
.
Begründe, warum der von dir gewählte Punkt die beiden Bedingungen erfüllt.
die beiden Bedingungen erfüllt.
Begründe, warum der von dir gewählte Punkt
(3 BE)
1.3 Analysis
Gegeben ist die in
(5 BE)
1.4 Analytische Geometrie
Gegeben ist die Ebene
a)
Prüfe, ob der Punkt  in
in  liegt.
liegt.
(1 BE)
b)
Beschreibe die Lage von  im Koordinatensystem.
im Koordinatensystem.
(2 BE)
c)
Bestimme diejenige reelle Zahl  , für die die Ebene
, für die die Ebene  senkrecht zu
senkrecht zu  steht.
steht.
(2 BE)
1.5 Analytische Geometrie
Gegeben sind die Punkte
a)
Zeige, dass es sich beim Dreieck  um ein gleichschenkliges Dreieck mit der Basis
um ein gleichschenkliges Dreieck mit der Basis  handelt.
handelt.
(2 BE)
b)
Das Dreieck  hat den Flächeninhalt
hat den Flächeninhalt  . Bestimme den Wert von
. Bestimme den Wert von  .
.
(3 BE)
1.4 Stochastik
In der Urne liegen vier rote und zwei grüne Kugeln.
a)
Aus der Urne werden nacheinander drei Kugeln zufällig gezogen, ohne dass die gezogenen Kugeln zurückgelegt werden.
Ermittle die Wahrscheinlichkeit dafür, dass mindestens eine der gezogenen Kugeln grün ist.
Aus der Urne wird eine Kugel entfernt, sie enthält also nur noch fünf Kugeln.
Ermittle die Wahrscheinlichkeit dafür, dass mindestens eine der gezogenen Kugeln grün ist.
(2 BE)
b)
Nun beträgt die Wahrscheinlichkeit, dass beim zufälligen Ziehen von zwei Kugeln ohne Zurücklegen zwei Kugeln mit verschiedenen Farben gezogen werden,  .
.
Entscheide, ob die entfernte Kugel rot oder grün ist. Begründe deine Entscheidung.
Entscheide, ob die entfernte Kugel rot oder grün ist. Begründe deine Entscheidung.
(3 BE)
1.5 Stochastik
a)
Unter denjenigen Kunden, die gerne in die Region A reisen, wird eine Person zufällig ausgewählt. Bestimme die Wahrscheinlichkeit dafür, dass diese Person auch gerne in die Region B reist.
(2 BE)
b)
Berechne den Anteil der Kunden, die entweder in die Region A oder in die Region B gerne reisen.
(3 BE)
(25 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?1.1 Analysis
a)
b)
Folgender Ansatz wird gewählt:  Für die Steigung
Für die Steigung  gilt
gilt  Ableitung bilden:
Ableitung bilden:
 Steigung an der Stelle
Steigung an der Stelle  :
:

 Um
Um  zu bestimmen, werden zusätzlich zu
zu bestimmen, werden zusätzlich zu  auch die Koordinaten von
auch die Koordinaten von  eingesetzt. Es ist
eingesetzt. Es ist 
 Daraus folgt:
Daraus folgt:
![\(\begin{array}[t]{rll}
5&=& (-1) \cdot 1 +c&\quad \scriptsize \mid\;+1 \\[5pt]
6&=& c
\end{array}\)](https://mathjax.schullv.de/94649f4aac54b1f6bf97db807112ee8b48fbaae2fd8c248c0736633457d278a0?color=5a5a5a) Daraus folgt die Gleichung der Tangente mit
Daraus folgt die Gleichung der Tangente mit 
1.2 Analysis
a)
b)
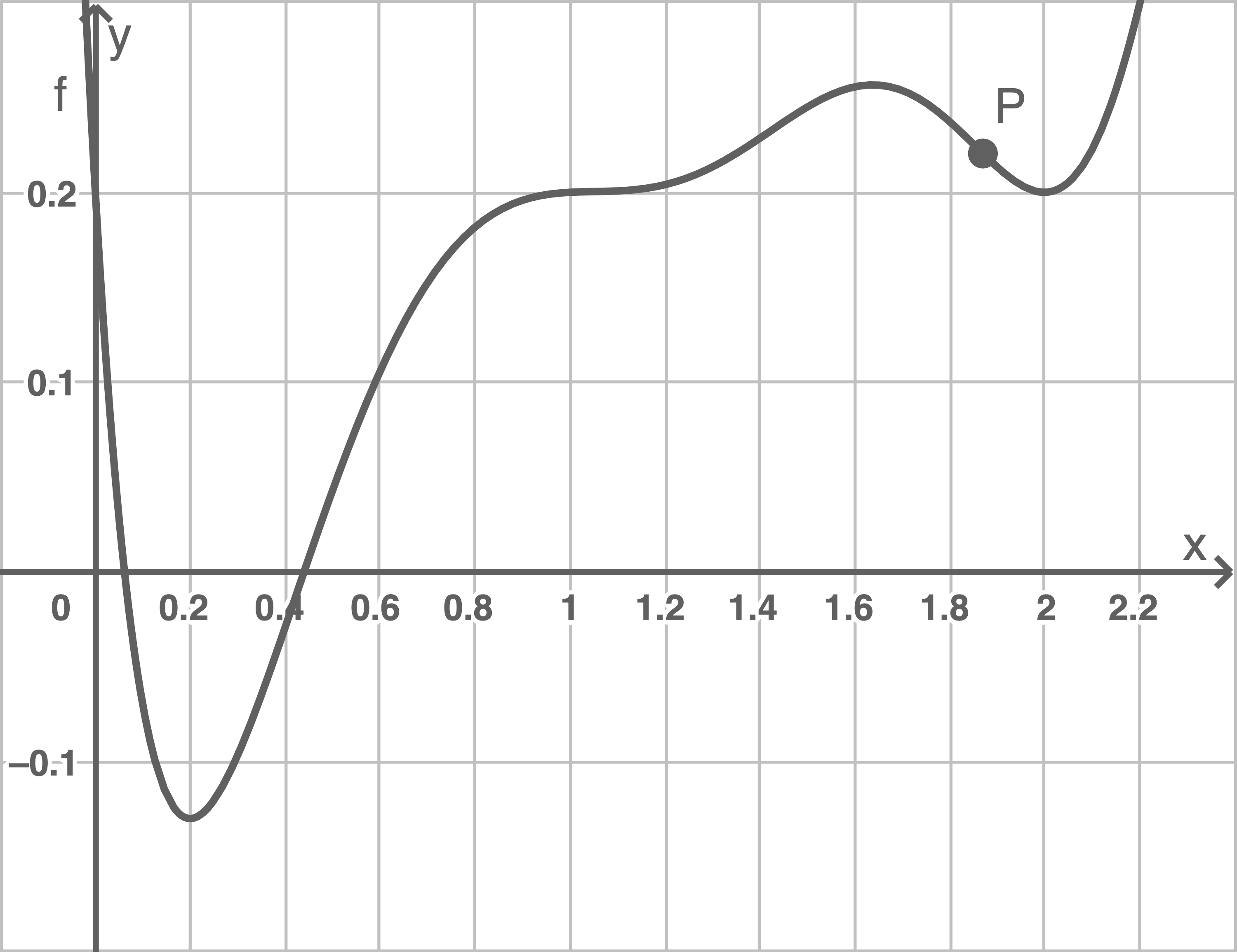
Mit  handelt es sich um einen Wendepunkt oder Sattelpunkt. Wegen
handelt es sich um einen Wendepunkt oder Sattelpunkt. Wegen  muss der Graph von
muss der Graph von  im Punkt
im Punkt  eine negative Steigung aufweisen. Folglich wird ein Punkt
eine negative Steigung aufweisen. Folglich wird ein Punkt  gewählt, der einem Wendepunkt mit negativer Steigung entspricht.
gewählt, der einem Wendepunkt mit negativer Steigung entspricht.
1.3 Analysis
1. Schritt: Schnittpunkte der Funktion1.4 Analytische Geometrie
a)
Punktprobe:
 Also liegt der Punkt in der Ebene
Also liegt der Punkt in der Ebene 
b)
Die Ebene  enthält die
enthält die  -Achse, da keine
-Achse, da keine  -Koordinate in der Koordinatenform vorkommt.
-Koordinate in der Koordinatenform vorkommt.
c)
Normalenvektoren der Ebenen sind  und
und  Die beiden Ebenen sind senkrecht zueinander, wenn ihr Skalarprodukt gleich Null ergibt.
Die beiden Ebenen sind senkrecht zueinander, wenn ihr Skalarprodukt gleich Null ergibt.
 Damit folgt:
Damit folgt:
![\(\begin{array}[t]{rll}
6+2s&=& 0 \quad \scriptsize \mid\; -6 \\[5pt]
2s&=& -6 \quad \scriptsize \mid\; :2\\[5pt]
s&=& -3
\end{array}\)](https://mathjax.schullv.de/73a8127794d3022ad4c196c6bf569ce7f9603ae44461adc533805ef44158e6fe?color=5a5a5a)
1.5 Analytische Geometrie
a)
b)
Der Mittelpunkt von  hat die Koordinaten
hat die Koordinaten 

 Der Flächeninhalt des Dreicks ist somit gegeben durch
Der Flächeninhalt des Dreicks ist somit gegeben durch  Es muss also gelten:
Es muss also gelten:
![\(\begin{array}[t]{rll}
5z&=& 35 &\quad \scriptsize \mid\; :5\\[5pt]
z&=& 7
\end{array}\)](https://mathjax.schullv.de/7ff99efaa2e31b71b723caa60a62a716b2a836fac15fe9f78d0172e77e78f51b?color=5a5a5a)
1.4 Stochastik
a)
b)
Angenommen, die entfernte Kugel wäre rot. Dann gilt:

 Es wurde also eine rote Kugel entfernt.
Es wurde also eine rote Kugel entfernt.
1.5 Stochastik
a)
b)
Der Anteil der Kunden, der gerne in beide Regionen reist, ist jeweils im Anteil der Kunden enthalten, der nur in eine der beiden Regionen gerne reist. Daher lässt sich der gesuchte Anteil wie folgt berechnen:
