Analysis 2.1 - Tank
Die Abbildung zeigt den Graphen der in 
definierten Funktion 
mit 
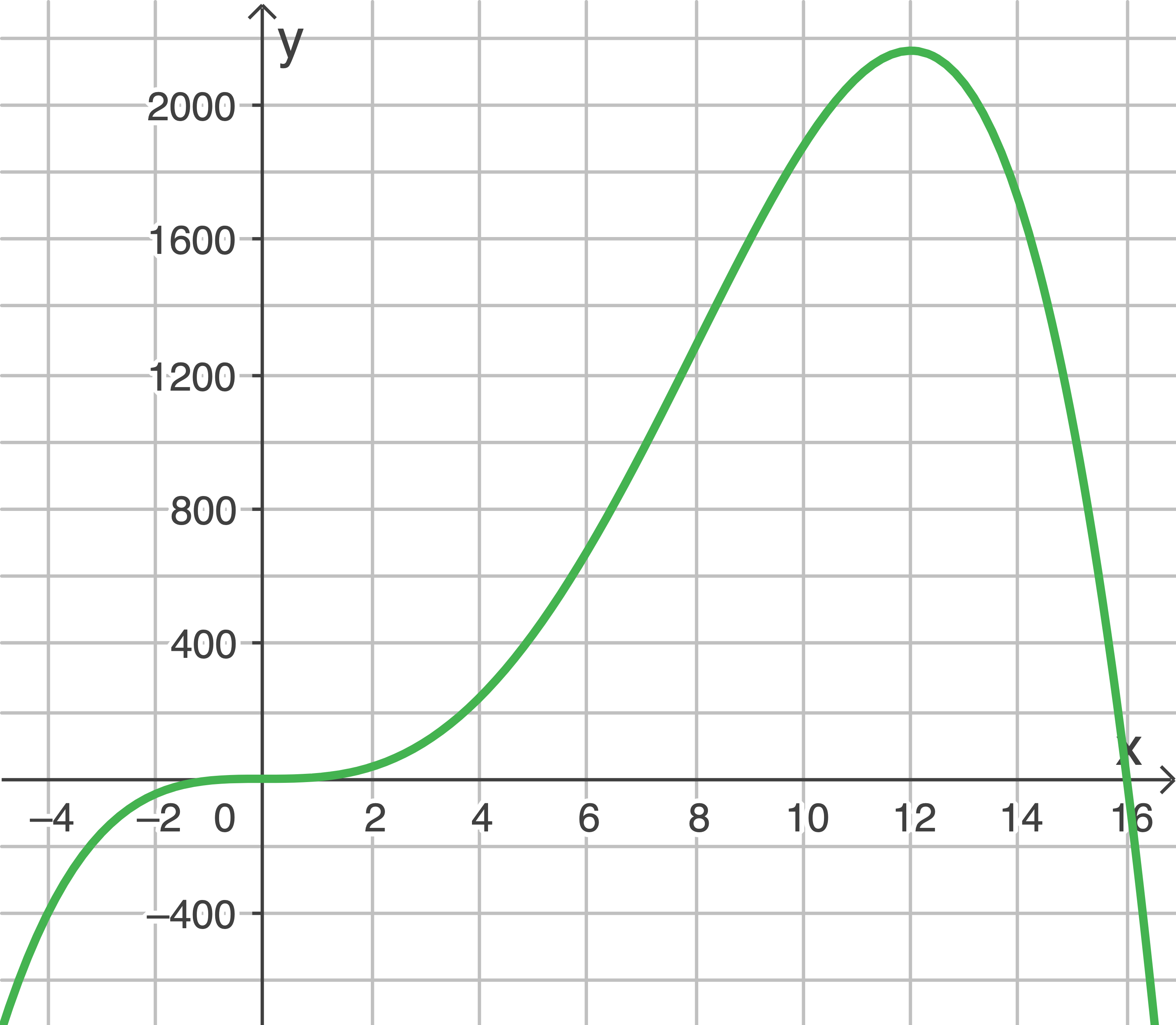
ist eine in definierte Funktion 
mit 
gegeben.
1
a)
Zeige rechnerisch, dass der Punkt 
ein Hochpunkt des Graphen von ist und dass die Tangente an den Graphen von im Punkt 
parallel zur 
-Achse verläuft.
(4 BE)
b)
Bestimme eine Gleichung der Geraden 
die durch die beiden Wendepunkte des Graphen von verläuft.
Zeichne in die Abbildung eine Gerade ein, die parallel zu
ist und für 
mit dem Graphen von genau einen Punkt gemeinsam hat.
(zur Kontrolle: Die Wendestellen sind 
und 
)
Zeichne in die Abbildung eine Gerade ein, die parallel zu
(5 BE)
c)
Beurteile die folgende Aussage:
Der Steigungswinkel des Graphen von im Punkt 
ist größer als der im Punkt 
(4 BE)
d)
Für jeden Wert von 
mit 
sind die Punkte 
und 
Eckpunkte eines Dreiecks
Zeige, dass der Flächeninhalt des Dreiecks mit der Gleichung
berechnet werden kann.
Zeige, dass der Flächeninhalt des Dreiecks mit der Gleichung
(4 BE)
e)
Berechne den maximalen Flächeninhalt des Dreiecks 
Für jede reelle Zahl
(6 BE)
f)
Beschreibe, wie der Graph von für 
aus dem Graphen von für 
erzeugt werden kann.
(2 BE)
g)
Bestimme denjenigen Wert von 
für den der Punkt 
auf dem Graphen von liegt.
(2 BE)
h)
Die Gleichungen I, II, III und IV liefern gemeinsam die Lösung einer Aufgabe.
oder 
Erläutere die Gleichungen und formuliere eine passende Aufgabenstellung.
I
II
III
IV
(5 BE)
i)
Die Gleichung 
für 
hat genau die drei Lösungen 
und 
und es gilt 
Deute dies mit Bezug auf die Graphen von und 
Deute dies mit Bezug auf die Graphen von
(3 BE)
2
Ein Unternehmen lagert Glyzerin in einem Tank. Die momentane Änderungsrate des Tankinhalts kann für 
mithilfe der Funktion aus Aufgabe 1 beschrieben werden. Dabei ist die seit Beobachtungsbeginn vergangene Zeit in Stunden und 
die momentane Änderungsrate in Kilogramm pro Stunde.
Zu Beobachtungsbeginn befinden sich im Tank 1200 kg Glyzerin.
Zu Beobachtungsbeginn befinden sich im Tank 1200 kg Glyzerin.
a)
Der Punkt 
liegt auf dem Graphen von 
Interpretiere die Koordinaten dieses Punkts im Sachzusammenhang.
Interpretiere die Koordinaten dieses Punkts im Sachzusammenhang.
(2 BE)
b)
Beurteile die folgende Aussage:
Zwölf Stunden nach Beobachtungsbeginn ist die größte Menge Glyzerin im Tank enthalten.
(2 BE)
c)
Bestimme grafisch unter Zuhilfenahme der Abbildung die Zunahme des Tankinhalts zwischen den Zeitpunkten acht Stunden und zehn Stunden nach Beobachtungsbeginn.
(3 BE)
d)
Berechne, wie viel Glyzerin 20 Stunden nach Beobachtungsbeginn im Tank enthalten ist.
(3 BE)
(45 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Hochpunkt
Damit ein Hochpunkt des Graphen von ist muss 
und 
erfüllt sein.
Damit sind alle Bedingungen für einen Hochpunkt erfüllt und der Punkt 
ist ein Hochpunkt des Graphen von .
Tangente
Die Tangente im Punkt 
hat die Steigung 
und verläuft somit parallel zur -Achse.
Vollständige Lösung anzeigen
b)
Mit dem notwendigen Kriterium für Wendestellen folgt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/362f447b4d65604b6bc67ec0e91ad31942a499b572c3ae6dd7ccc2c07fdae612?color=5a5a5a)
Mit dem Satz vom Nullprodukt folgt 
Die beiden Wendepunkte liegen also bei 
und 
Mit den zugehörigen Funktionswerten kann dann die Steigung der Geraden bestimmt werden:
und 
Da einer der Wendepunkte im Koordinatenursprung liegt, folgt für 
.
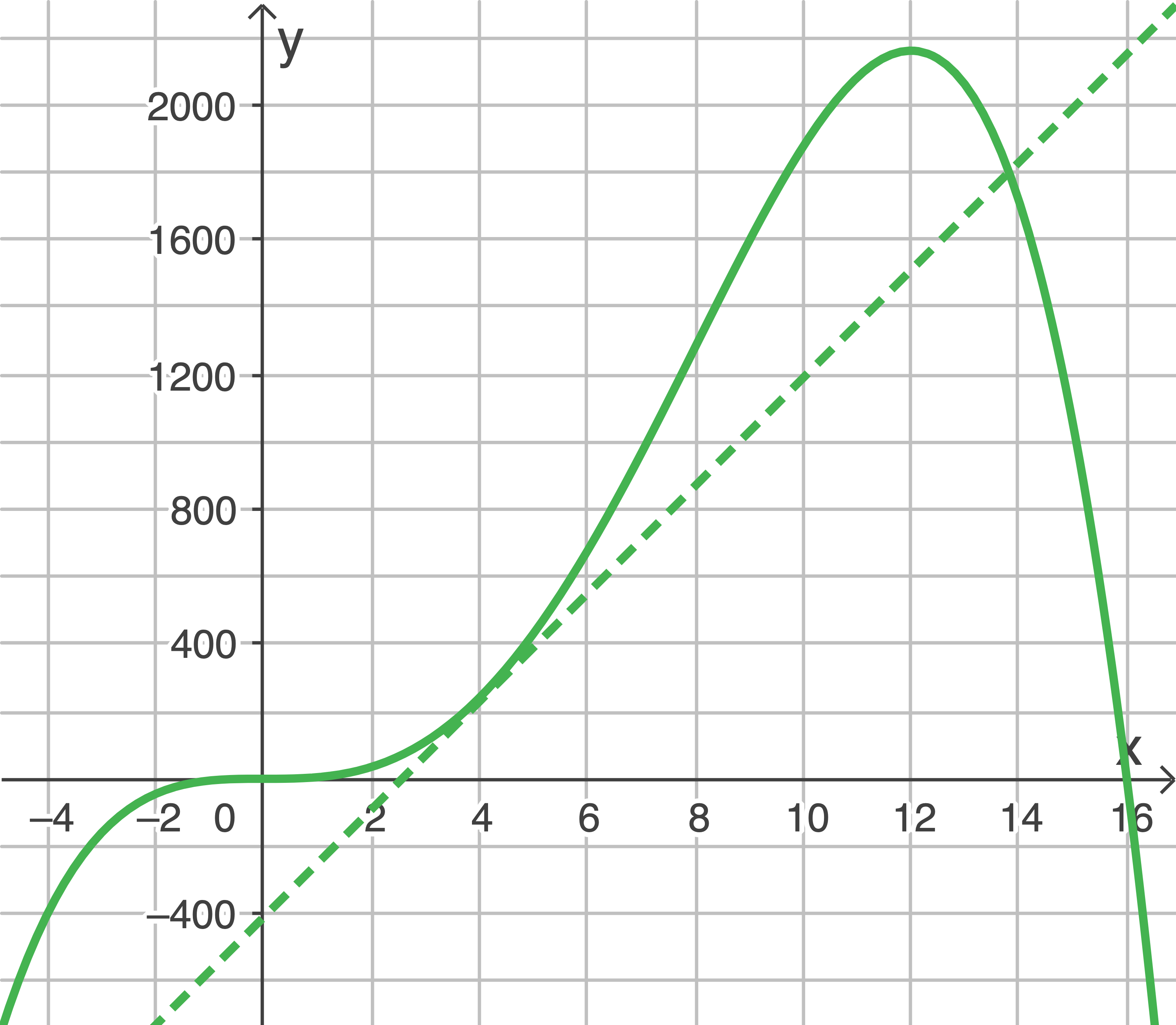
c)
Der Steigungswinkel des Graphen von an der Stelle 
lässt sich wie folgt berechnen:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& f](https://mathjax.schullv.de/bae84221876847ce6a9be3e5a7ab58e20005b83b93733e70364dc3c4abc63912?color=5a5a5a)
Außerdem liefert der Taschenrechner für die Gleichung 
die Lösungen 
und 
Daraus folgt, dass der Steigungswinkel an den Graphen von an der Stelle gleich dem an der Stelle ist.
Die Aussage ist also falsch.
d)
Aus den drei Punkten ergibt sich ein rechtwinkliges Dreieck mit der Höhe 
Die Länge der übrigen Kathete, die auf der -Achse liegt, wird durch den Wert 
bestimmt. Daraus ergibt sich eine Gleichung für den Flächeninhalt des Dreieck abhängig von 
![\(\begin{array}[t]{rll}
A(u)&=&\frac{1}{2}\cdot 4\cdot f(u)\\ &=&\frac{1}{2}\cdot4\cdot \left(-\frac{5}{16}u^4+5\cdot u^3\right)\\&=&-\frac{5}{8}u^4+10u^3
\end{array}\)](https://mathjax.schullv.de/1e103aa7c1a188ba86f41a8dcd8a6893aaf31603cad238d5359c72b560334e93?color=5a5a5a)
e)
Da
f)
Der Faktor kann den Graphen der Funktion in 
-Richtung strecken bzw. stauchen. Um aus dem Graph von für 
den Graphen von für zu erzeugen, muss der Graph um den Faktor 
in -Richtung gestreckt werden.
g)
h)
I: Hier werden die Funktionsterme von und gleichgesetzt.
II: Die Gleichung I wird so umgestellt, dass auf der linken Seite null steht und die rechte Seite ein Produkt ist. Dazu wird 
ausgeklammert.
III: Als nächstes werden alle Nullstellen bestimmt. Der Term wird null, wenn ein Faktor des Produkts null ist, also für und 
. Letzteres folgt aus 
.
IV: Für den Parameter wird der Ausdruck unter der Wurzel (die Diskriminante) und somit die Wurzel gleich null und die Gleichung aus I hat genau zwei Lösungen.
Eine passende Aufgabenstellung könnte zum Beispiel heißen:
Bestimme denjenigen Wert von für den die Graphen von und genau zwei gemeinsame Punkte haben.
i)
Die Graphen von und haben für 
genau drei gemeinsame Punkte bei 
und 
Da das Integral über der Differenz von und gleich null ist, folgt außerdem, dass die beiden Graphen für zwei Flächen mit gleichem Flächeninhalt einschließen. Die beiden Flächen liegen auf unterschiedlichen Seiten des Graphen von 
Lösung 2
a)
b)
Der Abbildung des Graphen von lässt sich entnehmen, dass die momentane Änderungsrate nach zwölf Stunden nach Beobachtungsbeginn zunächst weiter positiv ist. Damit ist die Aussage falsch, da aufgrund der postiviten Änderungsrate weiterhin Glyzerin in den Tank gelangt.
c)
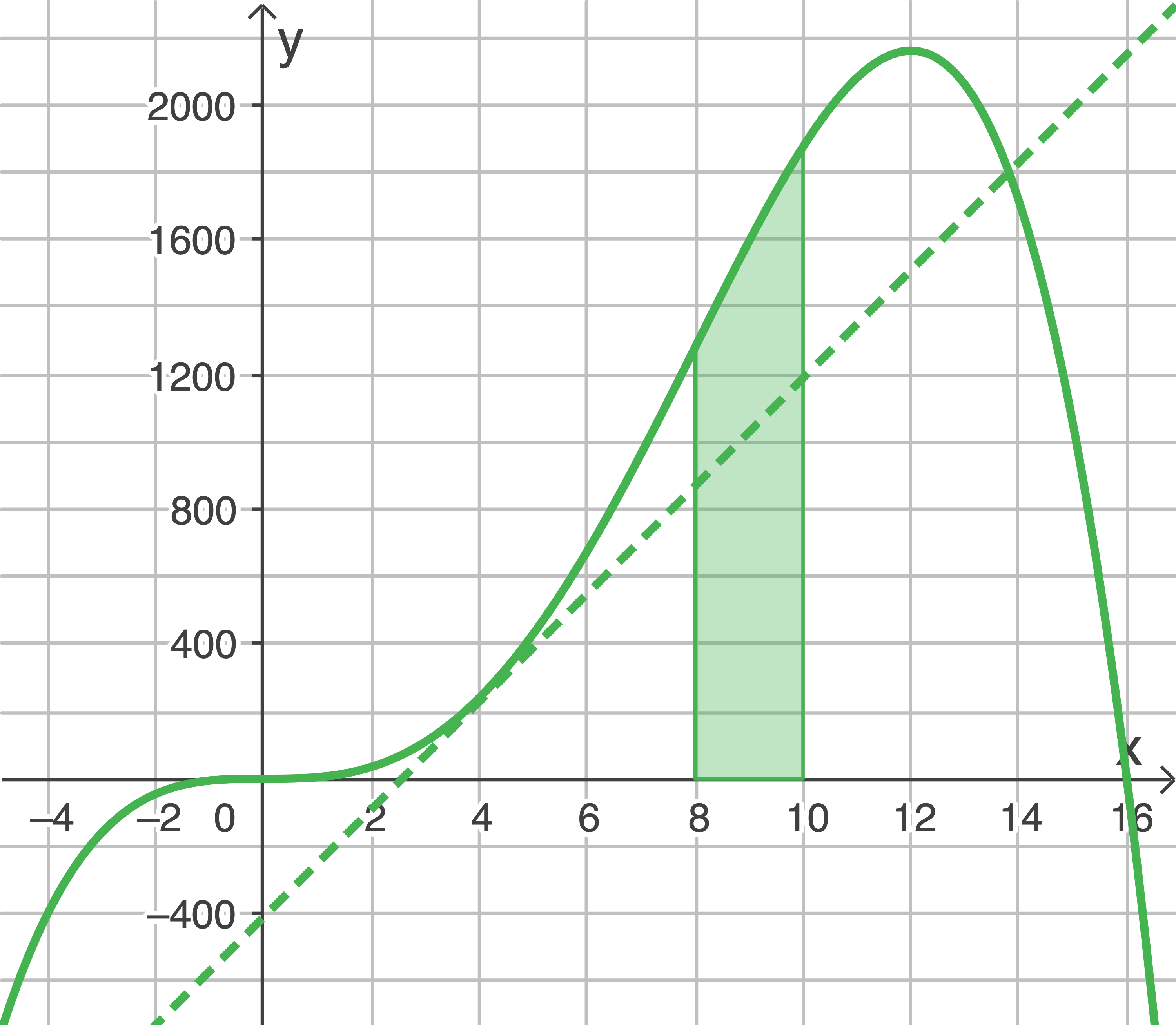
Die Zunahme des Tankinhalts lässt sich durch die eingeschlossene Fläche des Graphen von und der -Achse zwischen zwei Zeitpunkten bestimmen.
Die Fläche hat eine Größe von ca. 8 Kästchen. Ein Kästchen entspricht
Damit beträgt die Zunahme des Tankinhalts zwischen 
und 
Stunden nach Beobachtungsbeginn etwa 
Die Fläche hat eine Größe von ca. 8 Kästchen. Ein Kästchen entspricht
d)
Die Menge an Glyzerin nach 
Stunden kannst du mit dem Integral über der Funktion von berechnen.
Das heißt, dass der Tank Stunden nach Beobachtungsbeginn wieder genau so viel Glyzerin enthält wie zu Beobachtungsbeginn. Es befinden sich also nach Stunden 
Glyzerin im Tank.