Hilfsmittelfreier Teil

1.1 Analysis

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^3-x$ .

Einer der folgenden Graphen I, II und III stellt $f$ dar. Gib die Graphen an, die dafür nicht infrage kommen, und begründe deine Angabe.

Graph einer mathematischen Funktion mit den Achsen x und y.

Graf einer mathematischen Funktion mit x- und y-Achse, zeigt eine grüne Kurve.

Graph einer Funktion mit x- und y-Achse, zeigt eine steigende Kurve.

(2 BE)

Berechne den Inhalt der Fläche, die der Graph von $f$ und die $x$ -Achse einschließen.

(3 BE)

1.2 Analysis

Die Abbildung zeigt den Graphen einer Funktion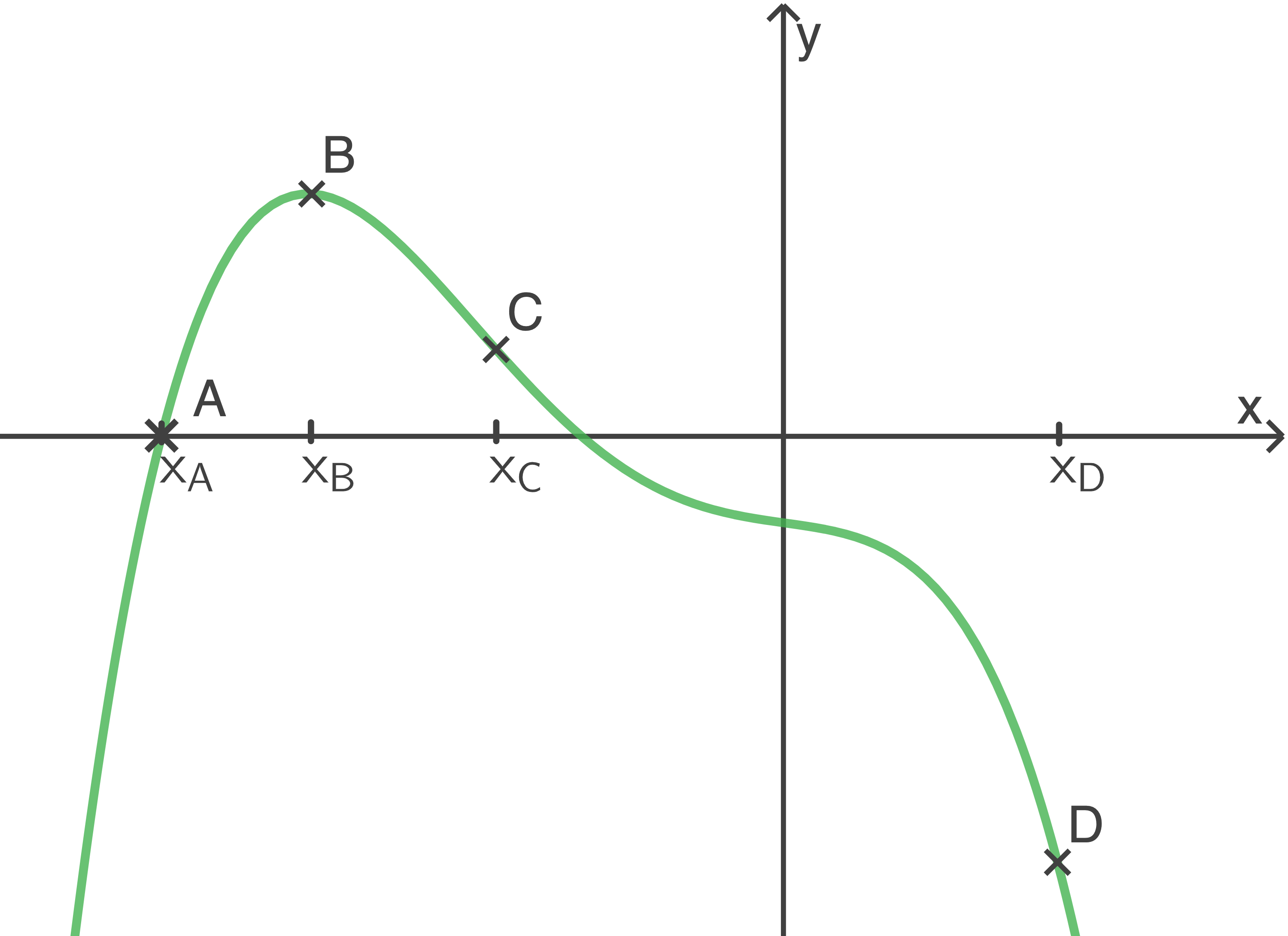 $f.$ Die Punkte $A,$ $B,$ $C$ und $D$ liegen auf dem Graphen von $f.$

Graph einer Funktion mit markierten Punkten A, B, C und D auf den Achsen x und y.

Gib an, ob die Funktionswerte der Ableitungsfunktion $\(f$ an den angegebenen Stellen positiv, negativ oder null sind.

	$\(f$
$x_A$
$x_B$
$x_C$

(3 BE)

Entscheide, ob die folgende Aussage wahr ist:

Für die bestimmten Integrale $I_1=\displaystyle\int_{x_A}^{x_C}f(x)\;\mathrm dx$ und $I_2=\displaystyle\int_{x_C}^{x_D}f(x)\;\mathrm dx$ gilt: $I_1\lt I_2.$

Begründe deine Entscheidung.

(2 BE)

1.3 Analysis

Gegeben ist die Funktion $f$ mit $f(x)=x^3-3x^2+4$ .

Zeige, dass $x_E=2$ eine der beiden Extremstellen der Funktion $f$ ist.

(2 BE)

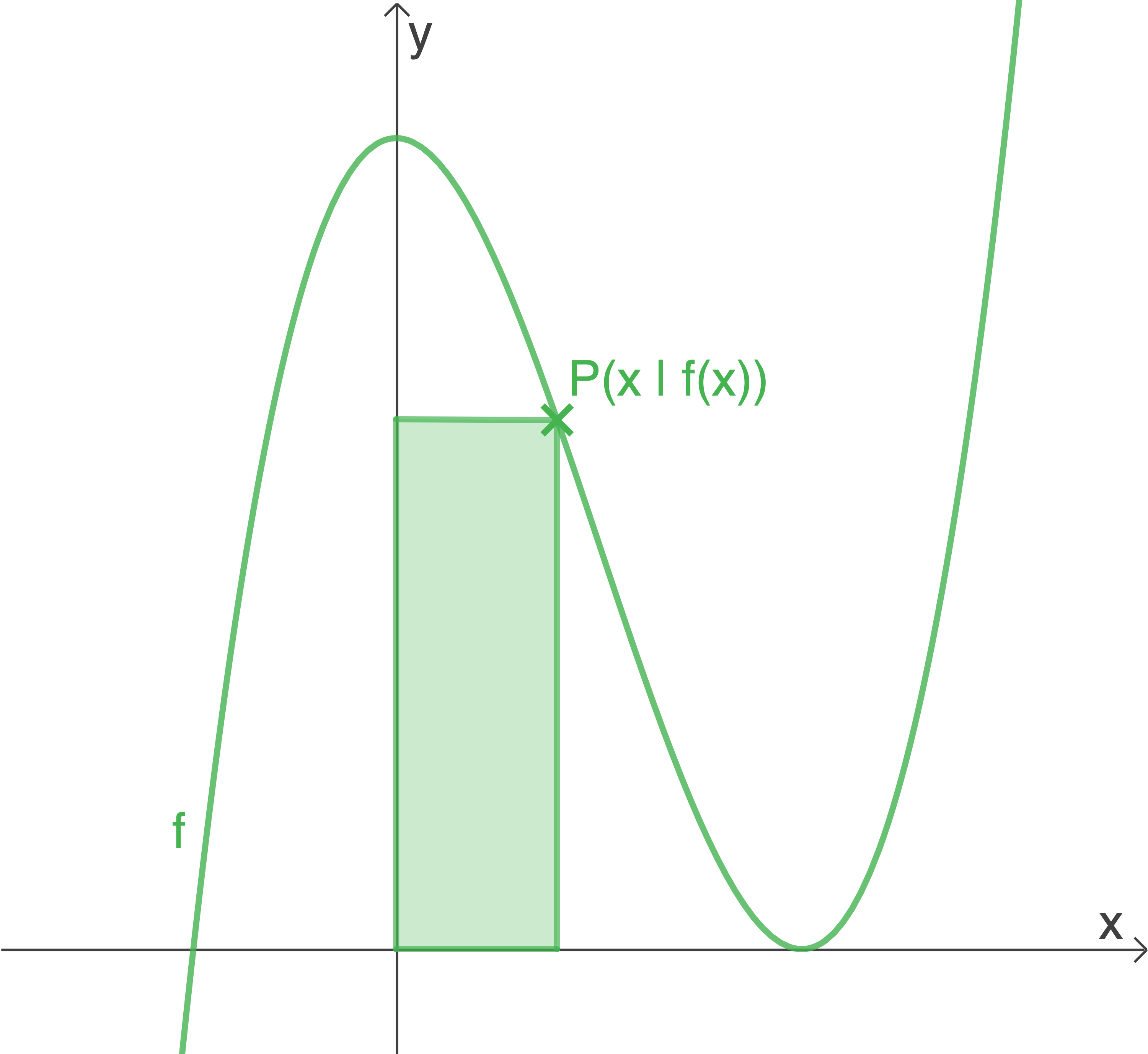
Jeder Punkt $P\left(x\mid f(x)\right)$ mit $0\lt x\lt2$ legt ein achsenparalleles Rechteck fest (siehe Abbildung).
Für genau einen Wert $x_\text{max}$ wird der Flächeninhalt dieses Rechtecks maximal.

Weise nach, dass gilt: $x_\text{max}\neq 1$ .

Grafik einer Funktion mit einem hervorgehobenen Punkt und einem Rechteck im Koordinatensystem.

(3 BE)

1.4 Analytische Geometrie

Zwei sich schneidende Ebenen sind gegeben durch ihre Gleichungen:

$E:\,2x+y+4z=6$ und $F:\,\left[\vec{x}-\pmatrix{1\\-8\\3}\right]\cdot\pmatrix{-5\\2\\8}=0$ .

Gib eine Gleichung der Ebene $F$ in Koordinatenform an.

(1 BE)

Die Gerade $s:\,\vec{x}=\pmatrix{1\\-4\\2}+r\cdot\pmatrix{0\\8\\-2}$ ; $r\in\mathbb{R}$ liegt in der Ebene $F$ .

Weise nach, dass die Gerade $s$ auch in der Ebene $E$ liegt.

(2 BE)

Ermittle eine Gleichung einer Ebene $H$ , die zu den beiden Ebenen $E$ und $F$ senkrecht verläuft.

(2 BE)

1.5 Analytische Geometrie

Gegeben ist der Punkt $P(4\mid6\mid4)$ und die Ebene $E:\,\vec{x}=\pmatrix{1\\2\\3}+t\cdot\pmatrix{0\\2\\1}+s\cdot\pmatrix{3\\0\\-1}$ ; $t,\,s\,\in\mathbb{R}$ .

Weise nach, dass der Punkt $P$ in der Ebene $E$ liegt.

(2 BE)

Die Gerade $g$

liegt in der Ebene $E$ ,
geht durch den Punkt $P$ und
hat keinen Schnittpunkt mit der xy-Ebene.

Gib eine Gleichung der Geraden $g$ an.

(3 BE)

1.4 Stochastik

Bei einem Spiel wird gleichzeitig mit einem roten und einem blauen Laplace-Würfel gewürfelt. Die Seiten beider Würfel sind mit den Augenzahlen von $1$ bis $6$ beschriftet.

Die Wahrscheinlichkeit, dass die Augenzahl des blauen Würfels größer ist als die des roten Würfels, beträgt $\frac{15}{36}$ .

Begründe, dass diese Aussage wahr ist.

(3 BE)

Die Zufallsgröße $X$ ist wie folgt definiert:

$X=0$ , wenn die Augenzahl des roten Würfels kleiner ist als die des blauen Würfels.
$X=1$ , wenn die Augenzahl beider Würfel gleich ist.
$X=2$ , wenn die Augenzahl des roten Würfels größer ist als die des blauen Würfels.

Ermittle den Erwartungswert der Zufallsgröße $X$ .

(2 BE)

1.5 Stochastik

In einer Urne befinden sich $6$ weiße und $4$ schwarze Kugeln.
Bei einem Auswahlverfahren ziehen $10$ Bewerber nacheinander ohne Zurücklegen eine Kugel aus dieser Urne. Jeder Bewerber, der eine weiße Kugel zieht, ist ausgewählt.

Der zweite Bewerber wird ausgewählt.
Zeige, dass die Wahrscheinlichkeit dafür $60\%$ beträgt.

(2 BE)

Entscheide, ob der erste oder der dritte Bewerber die größere Chance hat, ausgewählt zu werden. Begründe deine Entscheidung.

(3 BE)

(25 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1.1 Analysis

Es gilt: $f(0,5) = 0,5^3-0,5\lt 0.$ Damit kommt Graph II nicht infrage, da dieser für $x=0,5$ positiv ist.

Betrachtet man die Ableitung von $f$ für das Intervall $-0,5\leq x \leq 0,5$ , dann fällt auf, dass die Steigung des Graphens von $f$ hier nicht konstant sein kann, da $\(f$ Somit kommt Graph III für die Funktion $f$ ebenfalls nicht infrage.

Der Graph von $f$ schließt mit der $x$ -Achse zwei gleich große Flächen ein. Da Graph $1$ punktsymmetrisch zum Koordinatenursprung ist, reicht es, nur eine der beiden eingeschlossenen Flächen zu berechnen und diese dann zu verdoppeln.

$2\cdot\displaystyle\int_{-1}^{0}f(x)\;\mathrm dx=2\cdot\displaystyle\int_{-1}^{0}\left(x^3-x\right)\;\mathrm dx$ $=2\cdot\left[\frac{1}{4}x^4-\frac{1}{2}x^2\right]_{-1}^0=2\cdot\left(-\frac{1}{4}+\frac{1}{2}\right)$ $=\frac{1}{2}$

Lösung 1.2 Analysis

	$\(f$
$x_A$	positiv
$x_B$	null
$x_C$	negativ

Im Intervall von $x_A$ bis $x_C$ ist $f(x)\geq0$ und damit das Integral $I_1\geq0$ . Im Intervall von $x_C$ bis $x_D$ verläuft der Graph von $f$ größtenteils unterhalb der $x$ -Achse, sodass die eingeschlossene Fläche überwiegend unter der $x$ -Achse liegt. Damit ist der Wert des Integrals $I_2\lt 0$ und die Aussage $I_1\lt I_2$ ist falsch.

Lösung 1.3 Analysis

$\(f$

Das notwendige Kriterium für Extremstellen ist für $x=2$ erfüllt. Somit handelt es sich um eine der beiden Extremstellen von $f.$

Für jeden Punkt $P(x\mid f(x))$ kann der Inhalt des achsenparallelen Rechtecks wie folgt berechnet werden:

$A(x)=x\cdot f(x)$ $=x\cdot\left(x^3-3x^2+4\right)$ $=x^4-3x^3+4x$

$x_\text{max}$ muss das notwendige Kriterium für Extremstellen von $A$ erfüllen.

$\(A$

$x=1$ erfüllt das notwendige Kriterium für Extremstellen von $A$ nicht. Damit wird der Flächeninhalt für $x=1$ nicht maximal und es gilt $x_\text{max}\neq1.$

Lösung 1.4 Analytische Geometrie

Vollständigen Rechenweg anzeigen

$-5x+2y+8z = 3$

Eine Ebene in Koordinatenform der Ebene $F$ lautet $-5x+2y+8z=3.$

Einsetzen der Koordinaten von $s$ in die Ebenengleichung von $E:$

Vollständigen Rechenweg anzeigen

$6=6$

Damit ist die Aussage wahr. Die Gerade $s$ liegt in der Ebene $E$ .

Damit die Ebene $H$ senkrecht zu den beiden Ebenen $E$ und $F$ verläuft, müssen die Normalenvektoren $\overrightarrow{n_E}$ und $\overrightarrow{n_F}$ jeweils senkrecht zu $\overrightarrow{n_H}$ stehen. Ist das Skalarprodukt von zwei Vektoren gleich null, dann stehen sie senkrecht zueinander. Es muss also gelten:

$\overrightarrow{n_H}\cdot\overrightarrow{n_F}=0$ und $\overrightarrow{n_H}\cdot\overrightarrow{n_E}=0$

Daraus folgt:

$\begin{array}[t]{rll}\overrightarrow{n_H}\cdot\overrightarrow{n_F}&=&0\\[5pt] \pmatrix{h_1\\h_2\\h_3}\circ\pmatrix{-5\\2\\8}&=&0\\[5pt] -5h_1+2h_2+8h_3 &=&0\\[5pt] \end{array}$

und

$\begin{array}[t]{rll}\overrightarrow{n_H}\cdot\overrightarrow{n_E}&=&0\\[5pt] \pmatrix{h_1\\h_2\\h_3}\circ\pmatrix{2\\1\\4}&=&0\\[5pt] 2h_1+1h_2+4h_3 &=&0\\[5pt] \end{array}$

Ein Normalenvektor, der beide Gleichungen erfüllt ist beispielsweise $\overrightarrow{n_H} = \pmatrix{0\\8\\-2}.$

Eine mögliche Gleichung für eine Ebene $H$ ist zum Beispiel: $8y-2z=0.$

Lösung 1.5 Analytische Geometrie

Einsetzen des Ortsvektors von $P$ in die Geradengleichung liefert:

Vollständigen Rechenweg anzeigen

$\pmatrix{3\\4\\1} = ...$

Daraus folgt ein Gleichungssystem:

$\begin{array}[t]{rll} 3&=&3s\\ 4&=&2t\\ 1&=&t-s\\\\ \end{array}$

Dies lässt sich zu $s=1$ und $t=2$ lösen. Da das Gleichungssystem lösbar ist, liegt der Punkt $P$ in der Ebene $E$ .

Die Gerade $g$ schneidet die $xy$ -Ebene nicht, wenn alle Punkte auf ihr, die gleiche $z$ -Koordinate haben.

Es wird also ein weiterer Punkt $Q$ benötigt, der in $E$ liegt und die gleiche $z$ -Koordinate wie $P$ hat:

$Q(q_1\mid q_2\mid 4)$

Dazu müssen die Koordinaten des Punktes $Q$ folgendes Gleichungssystem lösen:

$\begin{array}[t]{rll} q_1&=& 1+ 3s\\ q_2&=& 2 +2t\\ 4&=& 3 + t-s\\ \end{array}$

Eine mögliche Lösung für den Punkt $Q$ ist z.B. $Q(1\mid4\mid4).$

Mit den Punkten $Q$ und $P$ folgt dann für eine Geradengleichung von $g:$

$g_{PQ}:\,\vec{x}=\pmatrix{4\\6\\4}+r\cdot\pmatrix{-3\\-2\\0}$ mit $r\in\mathbb{R}$ .

Lösung 1.4 Stochastik

Beim Wurf der zwei Würfel gibt es insgesamt $36$ verschiedene Kombinationen der Augenzahlen. Darunter sind $6$ Kombinationen, bei denen die Augenzahlen jeweils gleich sind. Es bleiben noch $30$ Kombinationen übrig, von denen die Hälfte zum Ereignis $A$ zählen, dass die Augenzahl des blauen Würfels größer ist als die des roten Würfels. Damit ergibt sich die Wahrscheinlichkeit für das Ereignis $A:$

$P(A)=\frac{15}{36}$

Die Aussage ist also wahr.

$E(X)$ $= 0\cdot \frac{15}{36}+1\cdot \frac{6}{36}+2\cdot\frac{15}{36}$ $=\frac{36}{36}$ $=1$

Lösung 1.5 Stochastik

s: Schwarze Kugel wird gezogen
w: Weiße Kugel wird gezogen

	$\frac{6}{10}$						$\frac{4}{10}$
		$w$				$s$
$\frac{5}{9}$			$\frac{4}{9}$	$\quad$	$\frac{6}{9}$			$\frac{3}{9}$
	$w$	$s$				$w$	$s$

Mit den Pfadregeln folgt:

$\frac{6}{10}\cdot\frac{5}{9}+\frac{4}{10}\cdot\frac{6}{9}$ $=\frac{54}{90}$ $=\frac{6}{10}$ $=60\,\%$

Damit beträgt die Wahrscheinlichkeit $60\,\%$ , dass der zweite Bewerber ausgewählt wird.

Die Wahrscheinlichkeit, ausgewählt zu werden, ist für den ersten Bewerber $\frac{6}{10}$ .

Für den dritten Bewerber gibt es insgesamt vier Zugfolgen, bei denen er ausgewählt wird: www, sww, ssw und wsw. Daraus lässt sich die Wahrscheinlichkeit für den dritten Bewerber berechnen:

$\frac{6\cdot5\cdot4}{10\cdot9\cdot8}$ $+\frac{4\cdot6\cdot5}{10\cdot9\cdot8}$ $+\frac{4\cdot3\cdot6}{10\cdot9\cdot8}$ $+\frac{6\cdot4\cdot5}{10\cdot9\cdot8}$ $=\frac{432}{720}$ $=\frac{6}{10}$

Beide Bewerber haben damit die gleiche Chance, ausgewählt zu werden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?