Analytische Geometrie 3 - Pyramide
Abbildung 1 zeigt die Pyramide  mit
mit 


 und
und 
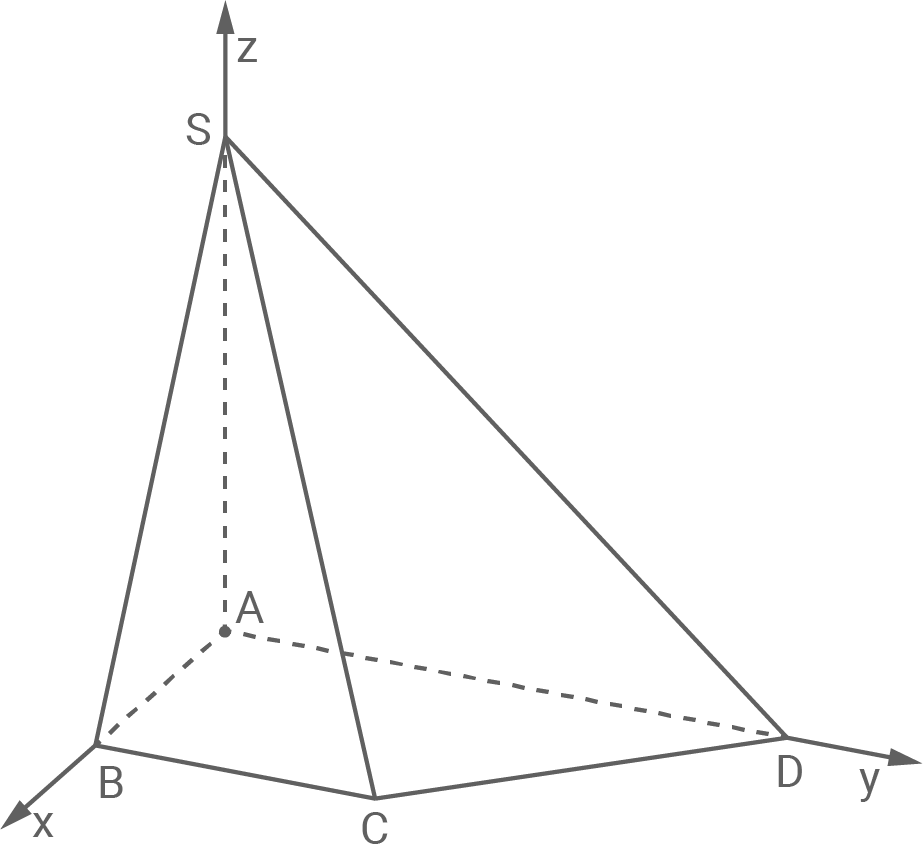

Abb. 1
a)
Begründe, dass die Grundfläche der Pyramide ein Trapez ist.
Berechne das Volumen der Pyramide.
Berechne das Volumen der Pyramide.
(4 BE)
b)
Zeige, dass das Dreieck  rechtwinklig ist.
rechtwinklig ist.
(2 BE)
c)
In Abbildung 2 ist ein Teil eines Netzes der Pyramide  dargestellt.
dargestellt.
Ergänze Abbildung 2 so, dass ein vollständiges Netz der Pyramide dargestellt ist.
dargestellt ist.
Ergänze Abbildung 2 so, dass ein vollständiges Netz der Pyramide
(3 BE)
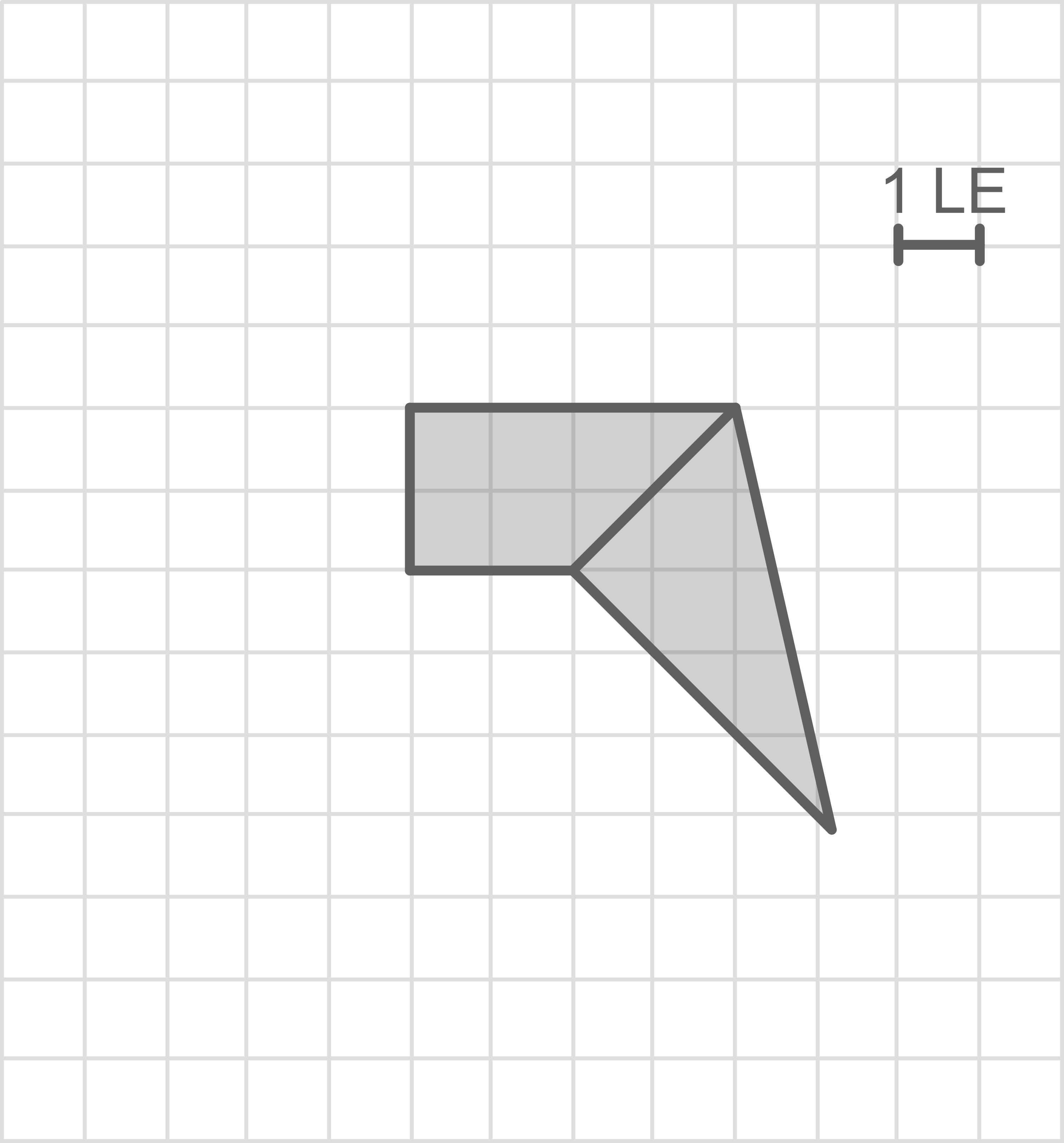
Abb. 2
d)
Bestimme eine Gleichung von  in Koordinatenform.
in Koordinatenform.
(zur Kontrolle:  )
)
(3 BE)
e)
Berechne die Größe des Winkels zwischen der Ebene  und der Ebene
und der Ebene  in der die Seitenfläche
in der die Seitenfläche  der Pyramide liegt.
der Pyramide liegt.
(3 BE)
f)
Betrachtet werden die Würfel, von denen drei Seitenflächen in den drei Koordinatenebenen liegen. Abbildung 3 zeigt einen dieser Würfel. Unter diesen Würfeln gibt es einen, bei dem ein Eckpunkt auf der Kante  der Pyramide liegt.
der Pyramide liegt.
Berechne die Kantenlänge dieses Würfels und begründe, dass kein Punkt dieses Würfels außerhalb der Pyramide liegt.
Berechne die Kantenlänge dieses Würfels und begründe, dass kein Punkt dieses Würfels außerhalb der Pyramide liegt.
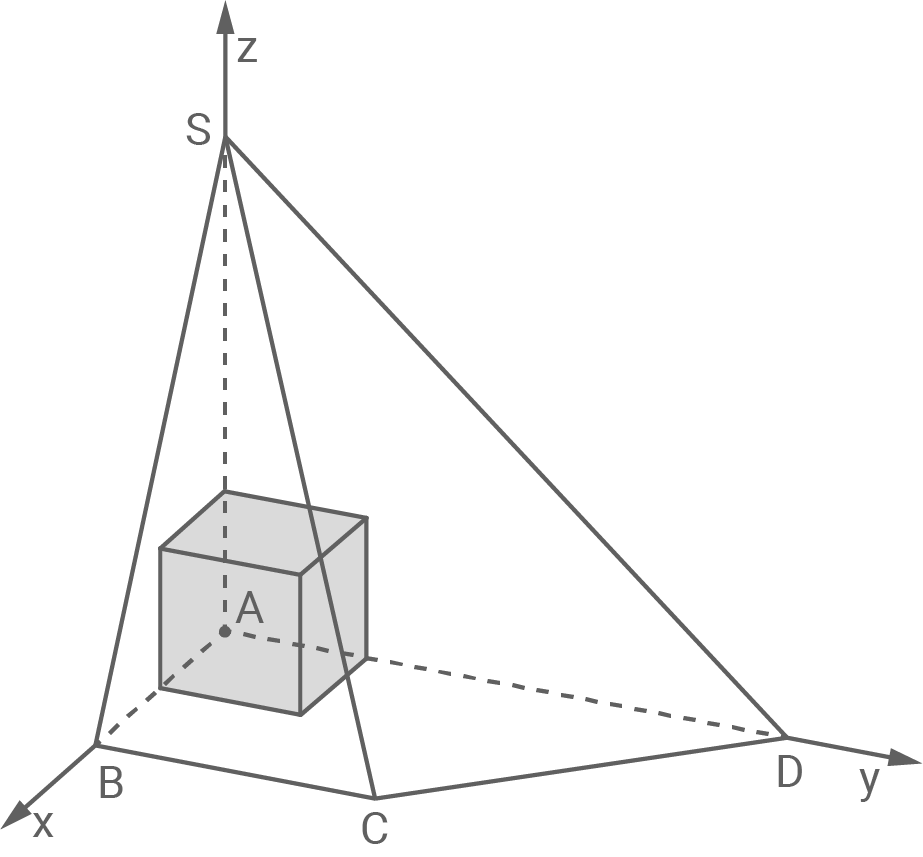
Abb. 3
(5 BE)
(20 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Trapezform der Grundfläche begründen
Die beiden Punktpaare  und
und  bzw.
bzw.  und
und  haben gleiche
haben gleiche  -Koordinaten, womit die beiden Seiten
-Koordinaten, womit die beiden Seiten  und
und  der Grundfläche parallel zueinander sind. Somit ist diese ein Trapez.
Volumen der Pyramide berechnen
Da die Grundfläche in der
der Grundfläche parallel zueinander sind. Somit ist diese ein Trapez.
Volumen der Pyramide berechnen
Da die Grundfläche in der  -Ebene liegt, ist die Höhe
-Ebene liegt, ist die Höhe  der Pyramide durch die
der Pyramide durch die  -Koordinate von
-Koordinate von  gegeben und beträgt somit
gegeben und beträgt somit  Die Länge der Seiten
Die Länge der Seiten  bzw.
bzw.  lassen sich aus den Koordinaten direkt als
lassen sich aus den Koordinaten direkt als  bzw.
bzw.  ablesen. Für die Länge von
ablesen. Für die Länge von  folgt:
folgt:
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{BC}\right\vert&=&\left\vert\pmatrix{2-2\\2-0\\0-0}\right\vert \\[5pt]
&=&\sqrt{0^2+2^2+0^2} \\[5pt]
&=&2\;[\text{LE}]
\end{array}\)](https://mathjax.schullv.de/30c03ea8857e121b7f26352aded986e07e26acf7e5551b65690bc5ebbe502daa?color=5a5a5a) Für das Volumen
Für das Volumen  der Pyramide folgt somit:
der Pyramide folgt somit:
![\(\begin{array}[t]{rll}
V&=& \dfrac{1}{3}\cdot G\cdot h \\[5pt]
&=&\dfrac{1}{3}\cdot\dfrac{(4+2)\cdot2}{2}\cdot3,5 \\[5pt]
&=& 7\;[\text{VE}]
\end{array}\)](https://mathjax.schullv.de/e0c9ea9553bc17dd1ec4006ad8087875df4aa859ca664ce49981122061a91ed6?color=5a5a5a)
b)
c)
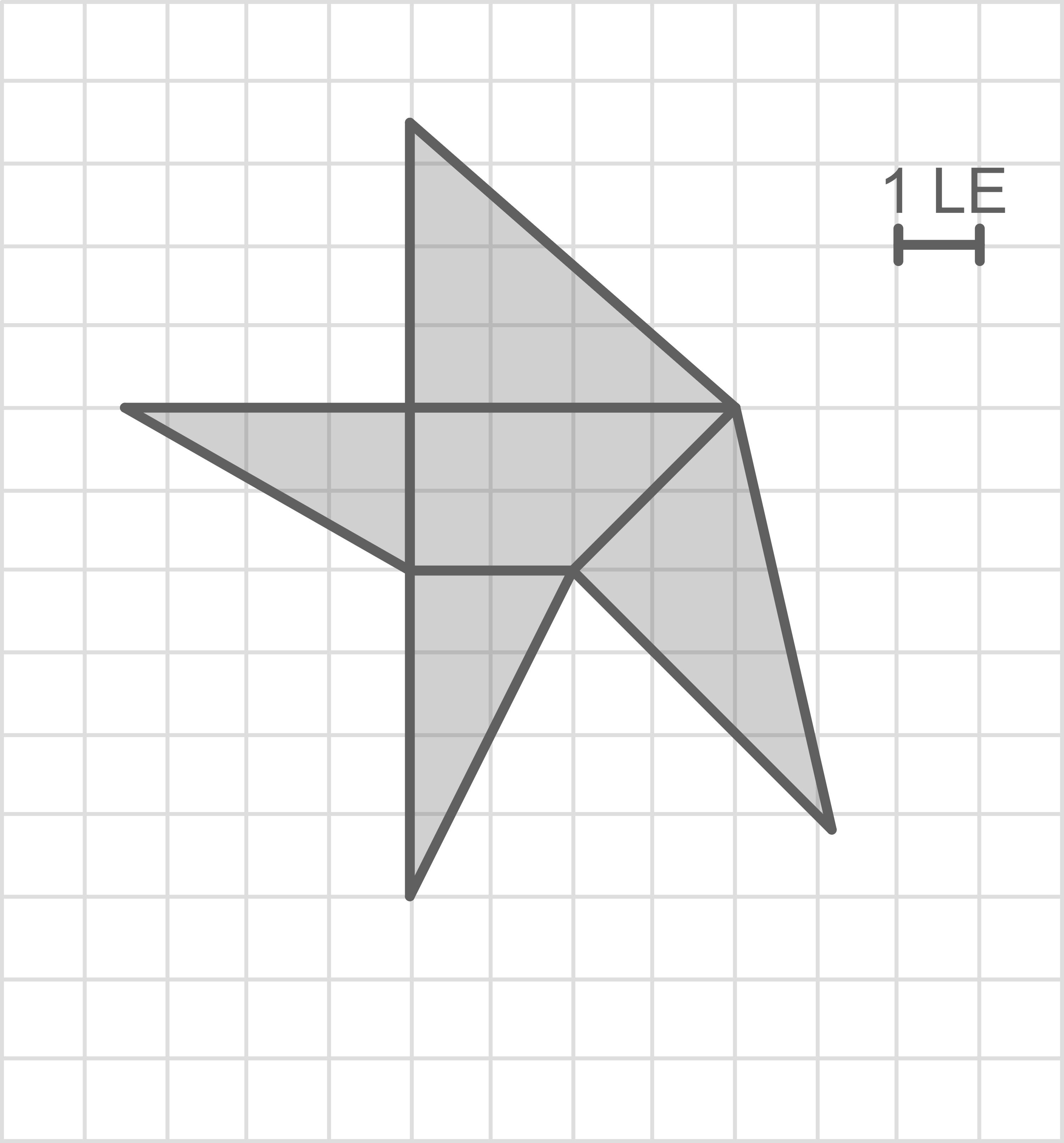
d)
Mit den Vektoren  und
und  aus Aufgabenteil b) folgt als ein Normalenvektor von
aus Aufgabenteil b) folgt als ein Normalenvektor von 
![\(\begin{array}[t]{rll}
\overrightarrow{n}&=&\overrightarrow{CD}\times\overrightarrow{CS} \\[5pt]
&=&\pmatrix{-2\\2\\0}\times\pmatrix{-2\\-2\\3,5} \\[5pt]
&=&\pmatrix{2\cdot3,5-0\\0-((-2)\cdot3,5)\\(-2)\cdot(-2)-(2\cdot (-2))} \\[5pt]
&=&\pmatrix{7\\7\\8}
\end{array}\)](https://mathjax.schullv.de/92443cf009323d3ebfb041e0ded010e0c9ebe70b724783bf7832ba205192d98a?color=5a5a5a) Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  in
in  liefert weiter:
liefert weiter:
![\(\begin{array}[t]{rll}
7\cdot0+7\cdot0+8\cdot3,5&=&c \\[5pt]
28&=&c
\end{array}\)](https://mathjax.schullv.de/347fafc947819b263269ded6c1c6442ad764d0e30e8b281fb805cc564562e041?color=5a5a5a) Somit ergibt sich
Somit ergibt sich  als eine Ebenengleichung von
als eine Ebenengleichung von  in Koordinatenform.
in Koordinatenform.
e)
Die Seitenfläche  liegt in der
liegt in der  -Ebene und besitzt somit den folgenden Normalenvektor:
-Ebene und besitzt somit den folgenden Normalenvektor:
 Mit dem Normalenvektor
Mit dem Normalenvektor  der Ebene
der Ebene  aus Aufgabenteil d) folgt für die Größe des Winkels zwischen den beiden Ebenen
aus Aufgabenteil d) folgt für die Größe des Winkels zwischen den beiden Ebenen  und
und 
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\left\vert\overrightarrow{n}\circ\overrightarrow{n_{yz}}\right\vert}{\left\vert\overrightarrow{n}\right\vert\cdot\left\vert\overrightarrow{n_{yz}}\right\vert} \\[5pt]
\cos(\alpha)&=&\dfrac{\left\vert\pmatrix{7\\7\\8}\circ\pmatrix{1\\0\\0}\right\vert}{\left\vert\pmatrix{7\\7\\8}\right\vert\cdot\left\vert\pmatrix{1\\0\\0}\right\vert} \\[5pt]
\cos(\alpha)&=&\dfrac{7}{\sqrt{162}\cdot\sqrt{1}} \\[5pt]
\alpha&=&\cos^{-1}\left(\dfrac{7}{\sqrt{162}}\right) \\[5pt]
\alpha&\approx&56,6^\circ
\end{array}\)](https://mathjax.schullv.de/c0bcaacab535100838e0410f2816127ea2ec7ffd81a2556583d53d28207a7441?color=5a5a5a)
f)
Kantenlänge des Würfels berechnen
Der Eckpunkt, welcher für einen bestimmten Würfel auf der Kante  liegt, besitzt die allgemeinen Koordinaten
liegt, besitzt die allgemeinen Koordinaten  Gleichsetzen mit der Gleichung der Geraden durch die Punkte
Gleichsetzen mit der Gleichung der Geraden durch die Punkte  und
und  liefert:
liefert:
![\(\begin{array}[t]{rll}
\pmatrix{k\\k\\k}&=&\overrightarrow{OC}+s\cdot\overrightarrow{CS} \\[5pt]
&=&\pmatrix{2\\2\\0}+s\cdot\pmatrix{-2\\-2\\3,5}
\end{array}\)](https://mathjax.schullv.de/37c124b5726c3dad5dc69be3d89f80e800c632da6b545de77405e9bcbb450f54?color=5a5a5a) Daraus ergibt sich folgendes Gleichungssystem:
Daraus ergibt sich folgendes Gleichungssystem:
 Addition von
Addition von  zu Gleichung
zu Gleichung  liefert:
liefert:
![\(\begin{array}[t]{rll}
2,75k&=&2\cdot1,75 &\quad \scriptsize \mid\;:2,75 \\[5pt]
k&=&\dfrac{14}{11}
\end{array}\)](https://mathjax.schullv.de/4799baffb7baf7817cd9061ffde74cf89b14164133705c99b279a865dfc5f42a?color=5a5a5a) Der Eckpunkt besitzt somit die Koordinaten
Der Eckpunkt besitzt somit die Koordinaten  womit die Kantenlänge des Würfels
womit die Kantenlänge des Würfels  beträgt.
Lage der Punkte des Würfels begründen
Die Abbildung zeigt, dass es reicht zu überprüfen, ob der Eckpunkt mit den Koordinaten
beträgt.
Lage der Punkte des Würfels begründen
Die Abbildung zeigt, dass es reicht zu überprüfen, ob der Eckpunkt mit den Koordinaten  außerhalb der Pyramide liegt oder nicht. Gleichsetzen mit der Gleichung der Geraden durch die Punkte
außerhalb der Pyramide liegt oder nicht. Gleichsetzen mit der Gleichung der Geraden durch die Punkte  und
und  liefert:
liefert:
![\(\begin{array}[t]{rll}
\pmatrix{\frac{14}{11}\\0\\\frac{14}{11}}&=&\overrightarrow{OB}+t\cdot\overrightarrow{BS} \\[5pt]
&=&\pmatrix{2\\0\\0}+s\cdot\pmatrix{-2\\0\\3,5}
\end{array}\)](https://mathjax.schullv.de/559d27eff193e292069e5a6a995c8ceb6deab02b9449046f333ff6e0104e5f4c?color=5a5a5a) Es ergibt sich folgendes Gleichungssystem:
Es ergibt sich folgendes Gleichungssystem:
 Aus Gleichung
Aus Gleichung  folgt:
folgt:
![\(\begin{array}[t]{rll}
\dfrac{14}{11}&=&3,5t &\quad \scriptsize \mid\;:3,5 \\[5pt]
\dfrac{4}{11}&=&t
\end{array}\)](https://mathjax.schullv.de/e69393e6beb8581ee1ac146a0a5bfb570a845af13d5fd447cc50a437a7631e02?color=5a5a5a) Einsetzen in Gleichung
Einsetzen in Gleichung  als Probe liefert:
als Probe liefert:
![\(\begin{array}[t]{rll}
\dfrac{14}{11}&=&2-2\cdot\dfrac{4}{11} \\[5pt]
\dfrac{14}{11}&=&\dfrac{22}{11}-\dfrac{8}{11} \\[5pt]
\dfrac{14}{11}&=&\dfrac{14}{11}
\end{array}\)](https://mathjax.schullv.de/425e376b00dc72fd37305b3d73d0efef9cddd6591cadf63b2c9f1e5576a7cfbc?color=5a5a5a) Somit ist
Somit ist  eine Lösung des Gleichungsystems, das heißt der Punkt mit den Koordinaten
eine Lösung des Gleichungsystems, das heißt der Punkt mit den Koordinaten  liegt auf der Kante
liegt auf der Kante  der Pyramide. Damit liegt kein Punkt des Würfels außerhalb der Pyramide.
der Pyramide. Damit liegt kein Punkt des Würfels außerhalb der Pyramide.