Analytische Geometrie 3.1 - Kirchturm

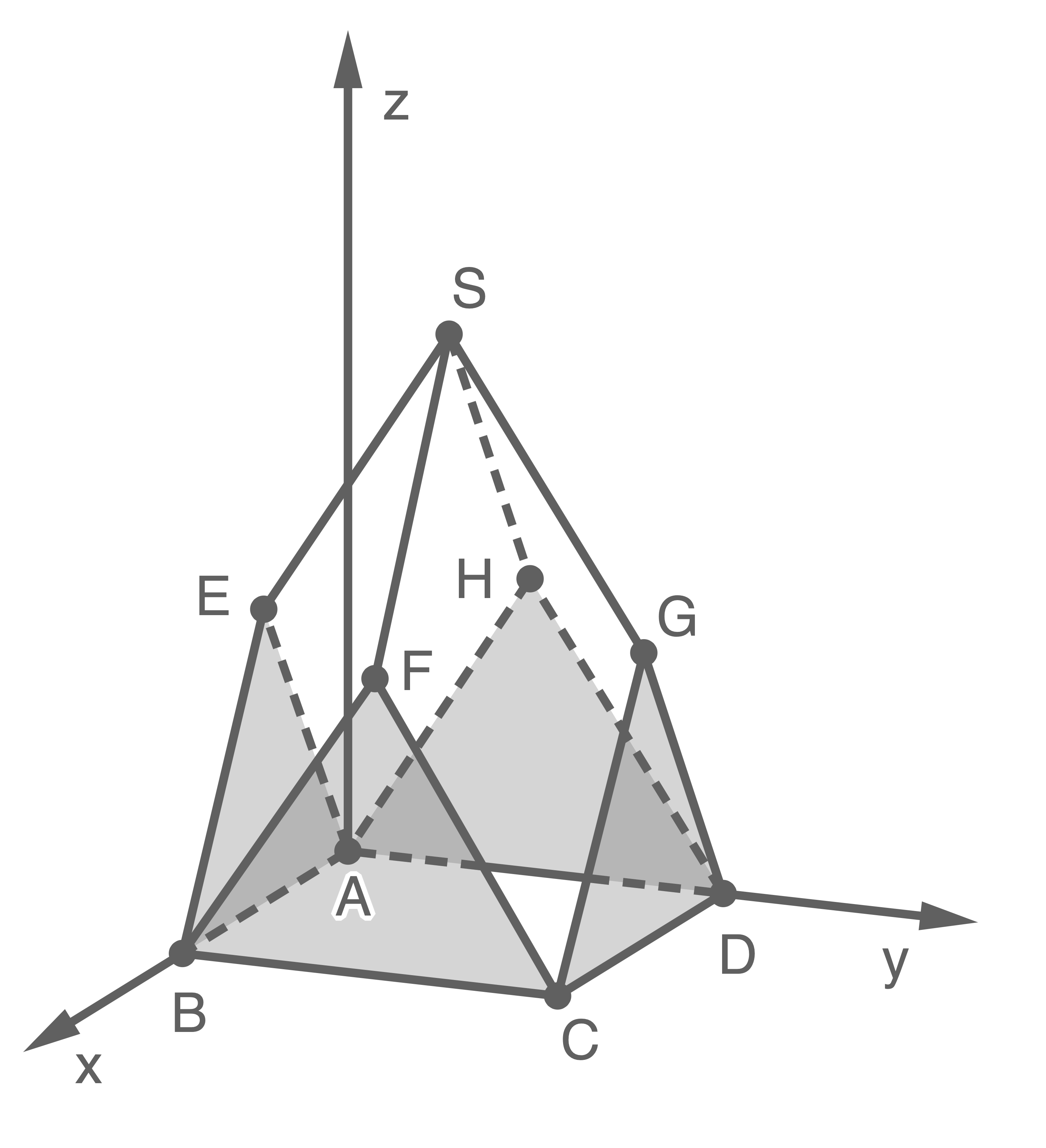
Die Abbildung zeigt modellhaft das Dach eines Kirchturms. Die Eckpunkte der dreieckigen Giebelflächen (markierte Fläche) und der viereckigen Dachflächen werden durch die Punkte $A$ , $B(8\mid 0\mid 0)$ , $C(8\mid 8\mid 0)$ , $D$ , $E(4\mid 0\mid 6)$ , $F(8\mid 4\mid 6)$ , $G(4\mid 8\mid 6)$ , $H$ und $S(4\mid 4\mid 12)$ dargestellt. Die vier Dachflächen haben die gleiche Form und die gleiche Größe.
Im verwendeten Koordinatensystem entspricht eine Längeneinheit einem Meter in der Realität. Die Materialstärken der Bauteile des Dachs sollen im Folgenden vernachlässigt werden.

Zeige, dass der Flächeninhalt des Quadrats $ABCD$ doppelt so groß ist wie der Flächeninhalt des Quadrats $EFGH$ .

(3 BE)

Die Ebene $L$ enthält die Punkte $C$ , $G$ und $F$ . Gib eine Gleichung von $L$ in Parameterform an und zeige, dass auch $S$ in $L$ liegt.

(3 BE)

Die Ebene $N$ verläuft parallel zur Ebene $L$ und geht durch den Punkt $B$ .

Weise nach, dass $\overrightarrow n= \pmatrix{3\\3\\2}$ ein Normalenvektor von $N$ ist und bestimme eine Gleichung von $N$ in Koordinatenform.

(3 BE)

Weise nach, dass das Viereck $CGSF$ eine Raute ist.

(2 BE)

Gegeben sind drei Ebenen mit den folgenden Gleichungen:
$M_1:x=8$ $M_2:x-y=0$ $M_3:z=6$
Eine dieser Ebenen stellt eine Symmetrieebene des Kirchendachs dar. Gib diese Ebene an und beschreibe ihre Lage.

(2 BE)

Berechne die Größe des Innenwinkels des Vierecks $CGSF$ im Punkt $S$ sowie den gesamten Flächeninhalt der Dachflächen.

(5 BE)

Die Gerade $q_1$ verläuft durch $S$ und $F$ , die Gerade $q_2$ durch $S$ und $G$ . Die beiden Geraden schneiden die $xy$ -Ebene in den Punkten $Q_1$ bzw. $Q_2$ .
Gib das Verhältnis des Abstands von $Q_1$ und $Q_2$ zum Abstand von $F$ und $G$ an.
Begründe deine Angabe.

(3 BE)

Begründe, dass das Gesamtvolumen des Kirchendachs mithilfe des Terms $\dfrac{1}{3}\cdot 128\,\text{m}^2\cdot 12\,\text{m} -4\cdot \dfrac{1}{3}\cdot16\,\text{m}^2\cdot \,\text{6m}$ berechnet werden kann.

(4 BE)

Zur Stabilisierung wird zwischen den durch $E$ und $G$ dargestellten Giebelspitzen ein gerader Stahlträger montiert. Vom Mittelpunkt dieses Stahlträgers aus soll eine möglichst kurze Stütze zum durch $\overline{SF}$ dargestellten Balken verlaufen. Der Punkt, in dem die Stütze auf den Balken trifft, wird im Modell mit $R$ bezeichnet, $R$ stimmt weder mit $F$ noch mit $S$ überein.
Berechne die Koordinaten von $R$ .

(5 BE)

(30 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\mid \overrightarrow{\mathrm{AB}}\mid = \mid \overrightarrow{\mathrm{BC}} \mid$ $= \left| \pmatrix{8\\0\\0} \right| =8\; [\mathrm{LE}]$

Daraus folgt der Flächeninhalt des Quadrates $ABCD$ mit $\mathrm{A}_{\mathrm{ABCD}}=64 \; \text{m}^{2}.$

$\mid \overrightarrow{\mathrm{EF}} \mid = \mid \overrightarrow{\mathrm{FG}} \mid$ $=\left| \pmatrix{4\\4\\0} \right| =\sqrt{32}\; [\text{LE}]$

Der Flächeninhalt des Quadrates $EFGH$ ergibt sich mit $\mathrm{A}_{\mathrm{EFGH}}=32=\frac{1}{2} \cdot \mathrm{A}_{\mathrm{ABCD}}.$

1. Schritt: Gleichung in Parameterfom aufstellen

$\overrightarrow{FC} = \pmatrix{0 \\ -4 \\ 6},$ $\overrightarrow{GC}= \pmatrix{-4 \\ 0 \\ 6}$

$L: \vec{x}=\pmatrix{8 \\ 8 \\ 0}+\lambda \cdot \pmatrix{0 \\ -4 \\ 6}+\mu \cdot \pmatrix{-4 \\ 0 \\ 6},$ $\lambda, \mu \in \mathbb{R}$

2. Schritt: Punktprobe

$\begin{array}[t]{rll} \pmatrix{4 \\ 4 \\ 12}&=& \pmatrix{8 \\ 8 \\0} +\pmatrix{ 0 \\ -4 \\ 6 }+\pmatrix{-4 \\ 0 \\ 6 } \\[5pt] &=&\pmatrix{4 \\ 4 \\ 12} \end{array}$

Somit liegt auch $S$ für $\lambda= \mu= 1$ in der Ebene $L.$

Wenn die Ebene $N$ parallel zur Ebene $L$ verläuft, so sind $\vec{n},$ $\overrightarrow{GC}$ und $\overrightarrow{FC}$ orthogonal:

$\pmatrix{3 \\ 3 \\ 2} \circ \pmatrix{0 \\ -4 \\ 6}$ $= 0+(-12)+12=0$

$\pmatrix{3 \\ 3 \\ 2} \circ \pmatrix{-4 \\ 0 \\ 6}$ $= (-12)+0+12=0$

Ebenengleichung aufstellen

$\begin{array}[t]{rll} 3 x+3 y+2 z&=& d &\quad \scriptsize \mid\; \text{B einsetzen} \\[5pt] 24&=&d \end{array}$

$N: 3 x+3 y+2 z=24$

Bei einer Raute sind zwei gegenüberliegende Seiten parallel und gleich lang.

$\overrightarrow{CF}=\pmatrix{0 \\ -4 \\ 6}=\overrightarrow{GS}$

$|\overrightarrow{CG}|=\left| \pmatrix{-4 \\ 0 \\ 6} \right|=|\overrightarrow{CF}|$

$M_{2}$ stellt eine Symmetrieebene dar. $M_{2}$ verläuft durch die Punkte $A, C$ und $S.$

Größe des Innenwinkels

$\cos (\varphi)$ $=\dfrac{ \pmatrix{4 \\ 0 \\ -6} \circ \pmatrix{0 \\ 4 \\ -6}}{\pmatrix{4 \\ 0 \\ -6} \pmatrix{0 \\ 4 \\ -6} }$ $=\dfrac{36}{52}$

Daraus folgt $\varphi= \cos^{-1} \left(\dfrac{36}{52} \right) \approx 46^{\circ}.$

Flächeninhalt der Dachfläche

$4 \cdot \dfrac{1}{2}\cdot |\overrightarrow{FG}| \cdot| \overrightarrow{CS}|$ $=2 \cdot \left| \pmatrix{-4 \\ 4 \\ 0} \right| \cdot \left|\pmatrix{-4 \\ -4 \\ 12} \right|$ $=2 \cdot \sqrt{32} \cdot \sqrt{176} \approx 150$

Der Flächeninhalt beträgt etwa $150 \; \text{m}^{2}$ .

Die Dreiecke $S Q_{1} Q_{2}$ und $SFG$ haben bei $S$ einen gemeinsamen Innenwinkel, die Gerade $Q_{1} Q_{2}$ ist parallel zur Gerade $FG.$

Damit sind die beiden Dreiecke ähnlich. $\overline{SQ_{1}}$ ist doppelt so lang wie $\overline{\mathrm{SF}}$ . Folglich ist der Abstand von $Q_{1}$ und $Q_{2}$ doppelt so groß wie der Abstand von $F$ und $G$ .

Die vier Geraden durch $S$ und die Punkte $E, F, G$ und $H$ bilden mit der $xy$ -Ebene eine Pyramide, deren quadratische Grundfläche eine Kantenlänge von $\sqrt{128} \; \text{m}$ hat. Der Term $\dfrac{1}{3} \cdot 128 \; \text{m}^{2} \cdot 12 \; \text{m}$ gibt das Volumen dieser Pyramide an.

Subtrahiert werden muss davon das Volumen von 4 gleich großen „kleinen“ Pyramiden mit dreieckiger Grundfläche. Jede dieser Pyramiden, z. B. die mit den Eckpunkten $B,$ $Q_{1}, C$ und $F$ hat ein Volumen von $\dfrac{1}{3} \cdot 16 \; \text{m}^{2} \cdot 6 \; \text{m}.$

Die Stütze ist genau dann möglichst kurz, wenn sie orthogonal zu dem durch $\overline{S F}$ dargestellten Balken steht. Zunächst wird also der Mittelpunkt $M$ des Stahlträgers $\overline{E G}$ bestimmt.

Die Koordinaten des Mittelpunkts von $\overline{EG}$ lauten $T (4 \mid 4 \mid 6).$

Da der Punkt $R$ auf dem Balken liegen soll, ergeben sich die Koordinaten zu $\overrightarrow{OR}= \overrightarrow{OS} +\sigma \cdot \overrightarrow{SF}.$

Die Stütze ist orthogonal, wenn $\overline{TR}$ orthogonal zu $\overline{SF}$ ist.

Es gilt also:

$\begin{array}[t]{rll} \overrightarrow{TR} \circ \overrightarrow{SF}&=&0 \\[5pt] (\overrightarrow{OR}-\overrightarrow{OT}) \circ \overrightarrow{SF}&=&0 \\[5pt] (\overrightarrow{OS} +\sigma \cdot \overrightarrow{SF}-\overrightarrow{OT}) \circ \overrightarrow{SF}&=&0 \end{array}$

Mit dem solve-Befehl des CAS ergibt sich $\sigma= \dfrac{9}{13}$ und somit:

$\overrightarrow{OR}$ $= \pmatrix{4\\4\\12} +\dfrac{9}{13} \cdot \pmatrix{4\\0\\-6}$ $=\pmatrix{\frac{88}{13}\\4 \\ \frac{102}{13}}$

Die Koordinaten von $R$ folgen mit $R\left(\frac{88}{13}\mid 4 \mid \frac{102}{13}\right).$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?