Hilfsmittelfreier Teil
1.1 Analysis
Betrachtet wird eine Funktion
a)
Gib eine Gleichung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  an und begründe deine Angabe.
an und begründe deine Angabe.
(2 BE)
b)
Die Tangenten  und
und  schließen mit der
schließen mit der  -Achse ein Dreieck ein. Bestimme den Umfang des Dreiecks.
-Achse ein Dreieck ein. Bestimme den Umfang des Dreiecks.
(3 BE)
1.2 Analysis
Die Abbildung zeigt den Graphen einer in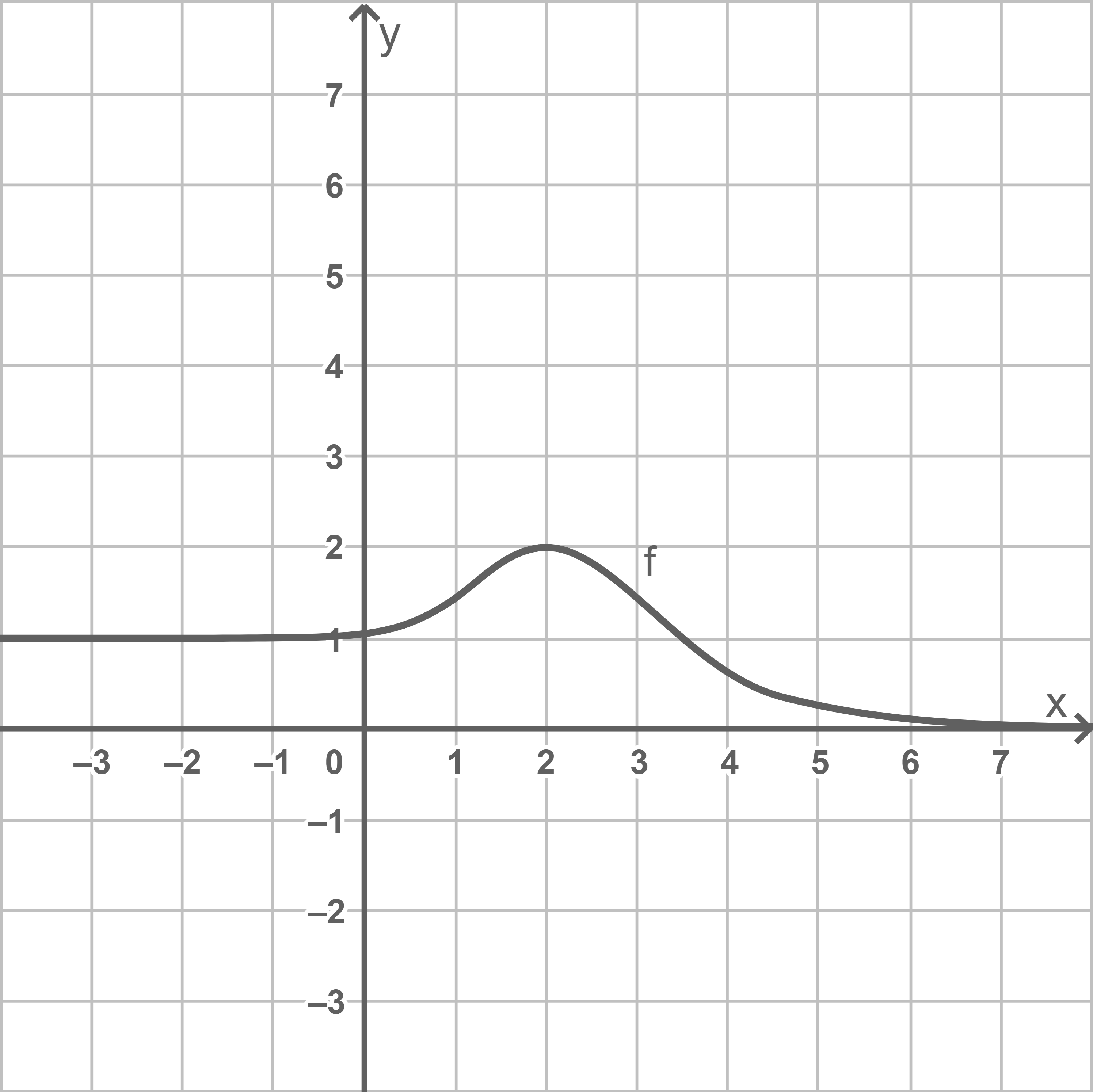
a)
Gib näherungsweise den Wert  an.
an.
(1 BE)
b)
Für eine Stammfunktion  von
von  gilt:
gilt:  Skizziere den Verlauf des Graphen dieser Stammfunktion in der Abbildung.
Skizziere den Verlauf des Graphen dieser Stammfunktion in der Abbildung.
(4 BE)
1.3 Analysis
Gegeben ist die in
a)
Die Funktion  hat genau zwei Extremstellen. Berechne diese.
hat genau zwei Extremstellen. Berechne diese.
(2 BE)
b)
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Begründe, dass die Graphen von
Begründe, dass die Graphen von  und
und  sich in dem Punkt
sich in dem Punkt  berühren.
berühren.
(3 BE)
1.4 Analytische Geometrie
Gegeben sind die Gerade
a)
Begründe, dass  nicht auf
nicht auf  liegt.
liegt.
(1 BE)
b)
Die Geraden  und
und  haben einen gemeinsamen Punkt. Ermittle den Wert von
haben einen gemeinsamen Punkt. Ermittle den Wert von 
(4 BE)
1.5 Analytische Geometrie
Gegeben sind die drei Eckpunkte eines Dreiecks
a)
Weise nach, dass der Abstand von  zu
zu  genauso groß ist wie der Abstand von
genauso groß ist wie der Abstand von  zu
zu 
(2 BE)
b)
Ermittle die Koordinaten eines Punktes  mit
mit  für den gilt:
für den gilt:




(3 BE)
1.4 Stochastik
In einer Urne liegen 5 Kugeln, davon 3 rote und 2 weiße. Die Kugeln unterscheiden sich nur durch ihre Farbe.
a)
Es werden zwei Kugeln mit Zurücklegen gezogen.
Ermittle die Wahrscheinlichkeit dafür, dass zwei gleichfarbige Kugeln gezogen werden.
Ermittle die Wahrscheinlichkeit dafür, dass zwei gleichfarbige Kugeln gezogen werden.
(2 BE)
b)
Bei einem anderen Zufallsexperiment werden aus der Urne nacheinander drei Kugeln ohne Zurücklegen gezogen.
Ermittle die Wahrscheinlichkeit dafür, dass unter den gezogenen Kugeln mehr rote Kugeln als weiße Kugeln sind.
Ermittle die Wahrscheinlichkeit dafür, dass unter den gezogenen Kugeln mehr rote Kugeln als weiße Kugeln sind.
(3 BE)
1.5 Stochastik
a)
Die Abbildung zeigt die Wahrscheinlichkeitsverteilung der binomialverteilten Zufallsgröße 
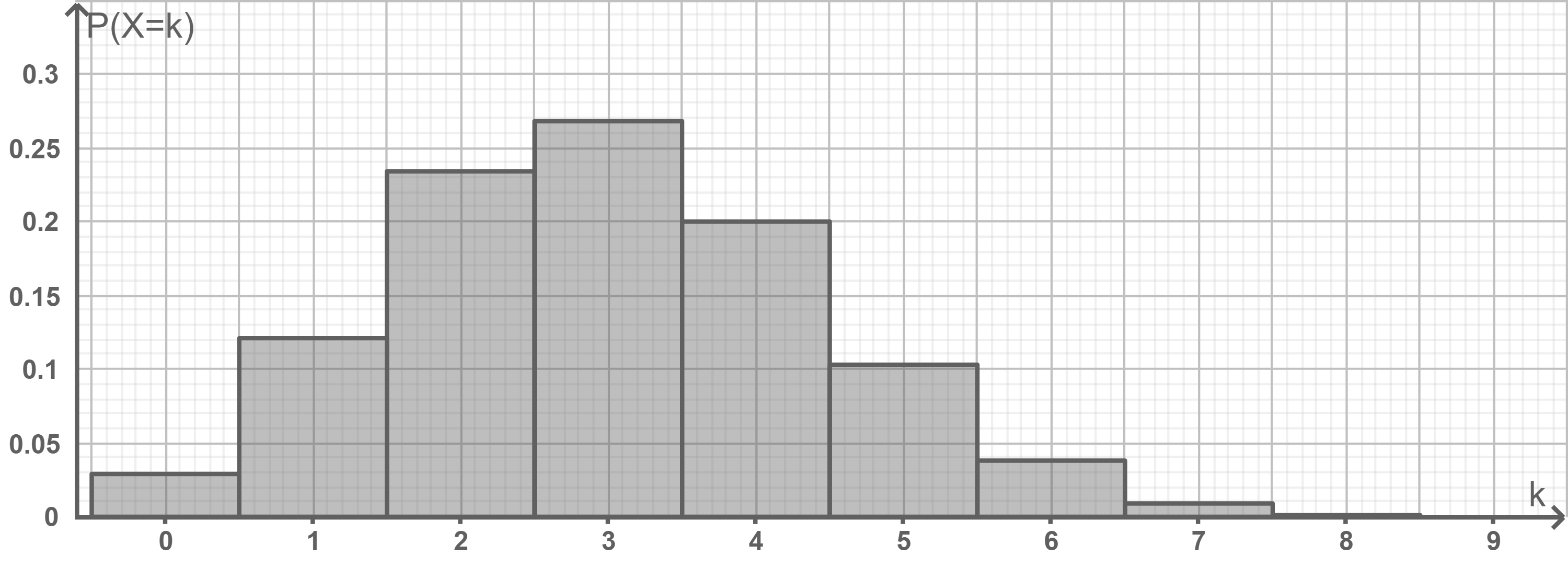 Bestimme näherungsweise
Bestimme näherungsweise 

(2 BE)
b)
Eine andere Zufallsgröße  ist binomialverteilt mit
ist binomialverteilt mit  und
und  Eine der folgenden Abbildungen zeigt die Wahrscheinlichkeitsverteilung der Zufallsgröße
Eine der folgenden Abbildungen zeigt die Wahrscheinlichkeitsverteilung der Zufallsgröße 
Entscheide begründet, welche Abbildung die Verteilung von zeigt.
zeigt.


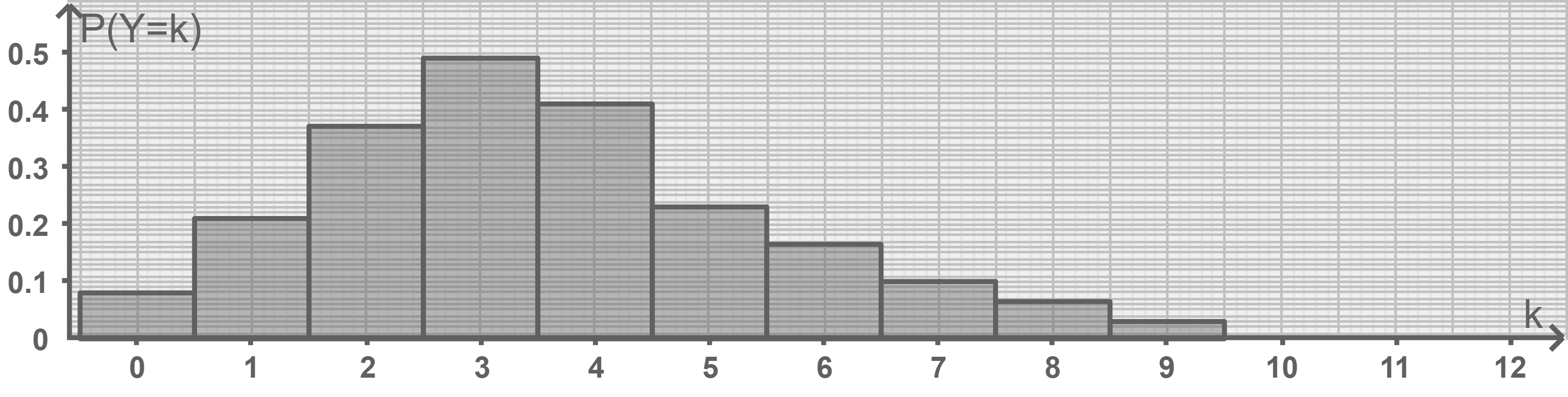
Entscheide begründet, welche Abbildung die Verteilung von



(3 BE)
(25 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?1.1 Analysis
a)
Da der Graph von  symmetrisch zur
symmetrisch zur  -Achse ist, entsteht die Tangente
-Achse ist, entsteht die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  durch Spiegelung der Tangente
durch Spiegelung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  an der
an der  -Achse.
-Achse.

 Eine Gleichung der Tangente an den Graphen von
Eine Gleichung der Tangente an den Graphen von  im Punkt
im Punkt  lautet demnach:
lautet demnach:
 Alternativer Lösungsweg
Da der Graph von
Alternativer Lösungsweg
Da der Graph von  symmetrisch zur
symmetrisch zur  -Achse ist, entsteht die Tangente
-Achse ist, entsteht die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  durch Spiegelung der Tangente
durch Spiegelung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  an der
an der  -Achse.
-Achse.
Für den Anstieg der Tangente an der Stelle gilt demnach:
gilt demnach:
 Da die Anstiege betragsmäßig gleich sind und die Berührstellen symmetrisch zum Koordinatenursprung liegen, schneiden sich beide Tangenten in ihrem Schnittpunkt mit der
Da die Anstiege betragsmäßig gleich sind und die Berührstellen symmetrisch zum Koordinatenursprung liegen, schneiden sich beide Tangenten in ihrem Schnittpunkt mit der  -Achse
-Achse  Für die gesuchte Tangentengleichung erhält man somit:
Für die gesuchte Tangentengleichung erhält man somit:

Für den Anstieg der Tangente an der Stelle
b)
1. Schritt: Schnittstelle von  mit der
mit der  -Achse bestimmen
-Achse bestimmen
![\(\begin{array}[t]{rll}
\dfrac{4}{3} \cdot x+4 &=& 0 &\quad \scriptsize \mid\; -4 \\[5pt]
\dfrac{4}{3} \cdot x &=& -4 &\quad \scriptsize \mid\; \cdot \dfrac{3}{4}\\[5pt]
x &=& -3
\end{array}\)](https://mathjax.schullv.de/883e9e875ff0fb1243aebf71ecc33b4aa6b93981dfab35127385573b64cd3da4?color=5a5a5a) 2. Schritt: Eckpunkte des Dreiecks bestimmen
Aufgrund der Symmetrie schneidet die Tangente
2. Schritt: Eckpunkte des Dreiecks bestimmen
Aufgrund der Symmetrie schneidet die Tangente  die
die  -Achse an der Stelle
-Achse an der Stelle 
Beide Tangenten schneiden die -Achse im Punkt
-Achse im Punkt 
Die Eckpunkte des Dreiecks sind also
 und
und  3. Schritt: Umfang des Dreiecks berechnen
3. Schritt: Umfang des Dreiecks berechnen
![\(\overline{S_1S_2} = 6\,\text{[LE]}\)](https://mathjax.schullv.de/cddfe646721d68099a278135d4318ac2c00ed2958fbddac65b54449823814158?color=5a5a5a)


![\(= \sqrt{25}=5\,\text{[LE]}\)](https://mathjax.schullv.de/ecc49aab344c9014a17a108e22a0474377f0d5e8aa1a04684308077c17eff3bd?color=5a5a5a)

Beide Tangenten schneiden die
Die Eckpunkte des Dreiecks sind also
1.2 Analysis
a)
In der Abbildung ist erkennbar, dass der Graph von  und die
und die  -Achse im Intervall
-Achse im Intervall ![\([0;2]\)](https://mathjax.schullv.de/843d839ab55e0f672f243636b5611ab923c075cc63ed4cbee0bdb8f535440b7a?color=5a5a5a) ungefähr 3 Kästchen einschließen. Daraus folgt:
ungefähr 3 Kästchen einschließen. Daraus folgt:

b)
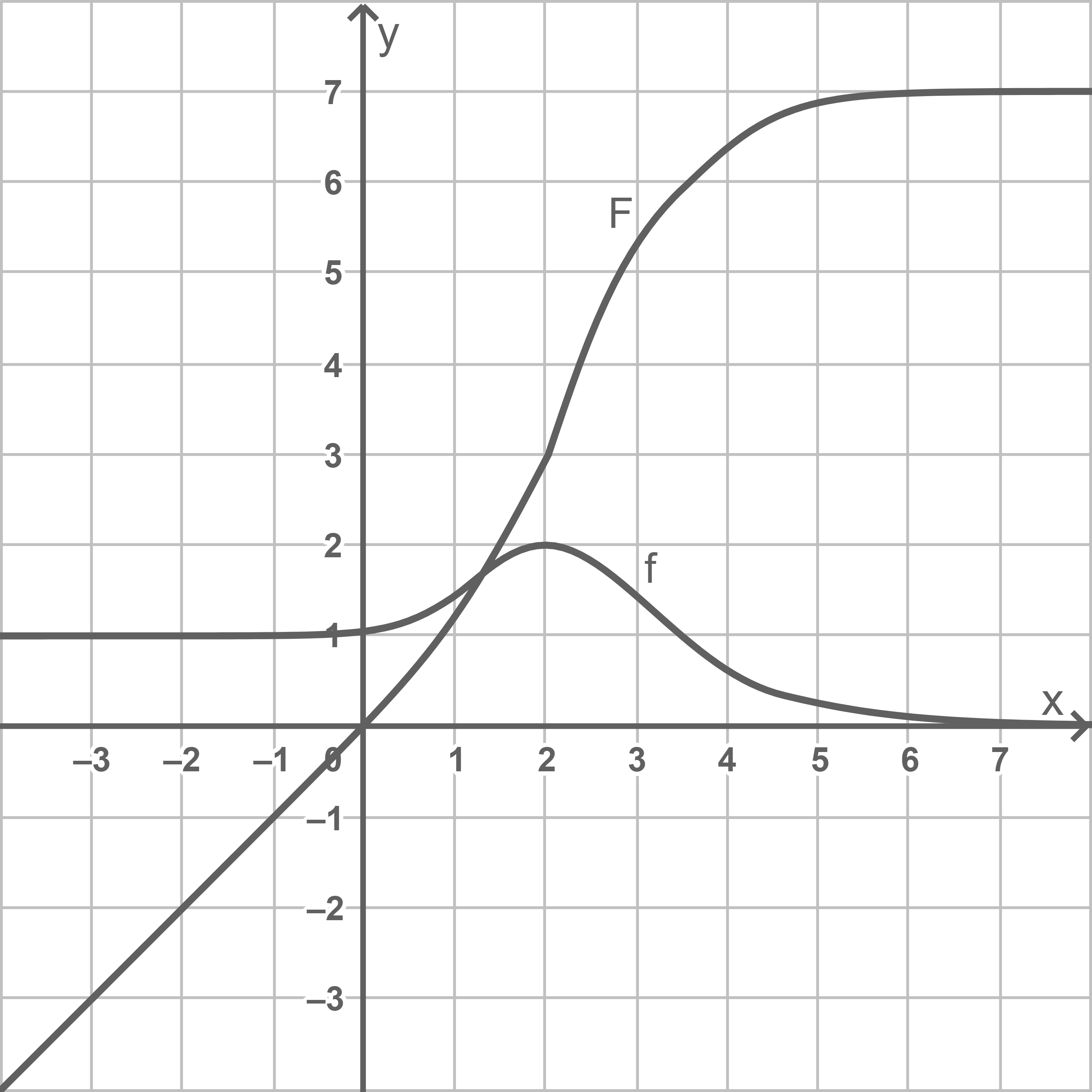
1.3 Analysis
a)
1. Schritt: Ableitung bilden
 2. Schritt: Notwendige Bedingung für Extremstellen anwenden
2. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/aa7a989989053d4c7a04ff2daaf770b3c09b504470a2acf9967fadea54e40281?color=5a5a5a) Mit der
Mit der  -Formel folgt:
-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1;2}&=&-\dfrac{-2}{2}\pm\sqrt{\left(\dfrac{-2}{2}\right)^2-0} \\[5pt]
x_{1;2}&=&1\pm\sqrt{1} \\[5pt]
x_1&=&2 \\[5pt]
x_2&=&0
\end{array}\)](https://mathjax.schullv.de/79360ec4cc368cb0376bd96378f260ece05b6a0b784d6d13534dbf74fdc5a5e7?color=5a5a5a) Laut Aufgabenstellungen existieren genau zwei Extremstellen von
Laut Aufgabenstellungen existieren genau zwei Extremstellen von  somit muss die hinreichende Bedingung nicht überprüft werden.
somit muss die hinreichende Bedingung nicht überprüft werden.
b)
Die Graphen von  und von
und von  berühren sich im Punkt
berühren sich im Punkt  wenn sie an der Stelle
wenn sie an der Stelle  denselben Funktionswert und die gleiche Steigung annehmen.
denselben Funktionswert und die gleiche Steigung annehmen.






 Es ist
Es ist  und somit
und somit  Damit ist der Punkt
Damit ist der Punkt  ein Berührpunkt von
ein Berührpunkt von  und
und 
1.4 Analytische Geometrie
a)
Die  -Koordinate von
-Koordinate von  ist Null, während die
ist Null, während die  -Koordinaten aller Punkte die auf
-Koordinaten aller Punkte die auf  liegen den Wert
liegen den Wert  haben.
haben.
b)
Eine Geradengleichung von  ergibt sich zu
ergibt sich zu 
 und
und  gleichsetzen:
gleichsetzen:
![\(\begin{array}[t]{rll}
\pmatrix{2\\3\\-7}+s\cdot \pmatrix{1\\0\\5}&=& \pmatrix{4\\0\\0}+r\cdot \pmatrix{1\\1\\b}
\end{array}\)](https://mathjax.schullv.de/d06bfcc7215c7b81505b0b7f352ad51c7996b1b09457d6e58f728f3fc98d7f02?color=5a5a5a) Daraus ergibt sich folgendes LGS:
Daraus ergibt sich folgendes LGS:
![\(\begin{vmatrix}
2+s&=& 4+r\\[5pt]
3&=&r \\[5pt]
-7+5s&=& r\cdot b
\end{vmatrix}\)](https://mathjax.schullv.de/f5f2f5c31c0e5f79da163b5811ef6c09b9304daab29aec4577948e3000190768?color=5a5a5a) Aus der ersten Zeile folgt
Aus der ersten Zeile folgt  Einsetzen in die erste Zeile:
Einsetzen in die erste Zeile:
![\(\begin{array}[t]{rll}
2+s&=& 4+3&\quad \scriptsize \mid\;-2 \\[5pt]
s&=&5
\end{array}\)](https://mathjax.schullv.de/bfb4bcde1071591e560fe6a33a88e00ebf88e4b27b75f8c92e75edd200c47e8c?color=5a5a5a)
 und
und  in die letzte Zeile des LGS einsetzen:
in die letzte Zeile des LGS einsetzen:
![\(\begin{array}[t]{rll}
-7+5s&=& r\cdot b \\[5pt]
-7+5\cdot 5&=& 3\cdot b&\quad \scriptsize \mid\;:3 \\[5pt]
6&=& b\\[5pt]
b&=& 6
\end{array}\)](https://mathjax.schullv.de/d2f4662600f9d9eeacacaa02e6460009551fed9b17fb254c00ec495779266f8d?color=5a5a5a)
1.5 Analytische Geometrie
a)
b)
Eine Möglichkeit einen solchen Punkt  zu ermitteln, besteht darin, den Punkt
zu ermitteln, besteht darin, den Punkt  am Mittelpunkt der Strecke
am Mittelpunkt der Strecke  zu spiegeln.
zu spiegeln.







 Der Punkt
Der Punkt  hat somit die Koordinaten
hat somit die Koordinaten 
1.4 Stochastik
a)
b)
Addition der Wahrscheinlichkeiten für drei rote Kugeln und zwei rote Kugeln liefert:







1.5 Stochastik
a)
b)
Die gesuchte Darstellung zeigt die höchste Wahrscheinlichkeit beim Erwartungswert.
Der Erwartungswert ist hierbei 


 Die Abbildung 1 besitzt die größte Wahrscheinlichkeit für
Die Abbildung 1 besitzt die größte Wahrscheinlichkeit für  kann es also nicht sein.
Abbildung 2 und Abbildung 3 erfüllen die Vorgabe, allerdings gilt bei Abbildung 3 in etwa:
kann es also nicht sein.
Abbildung 2 und Abbildung 3 erfüllen die Vorgabe, allerdings gilt bei Abbildung 3 in etwa:


 Somit zeigt Abbildung 2 die Verteilung von
Somit zeigt Abbildung 2 die Verteilung von 