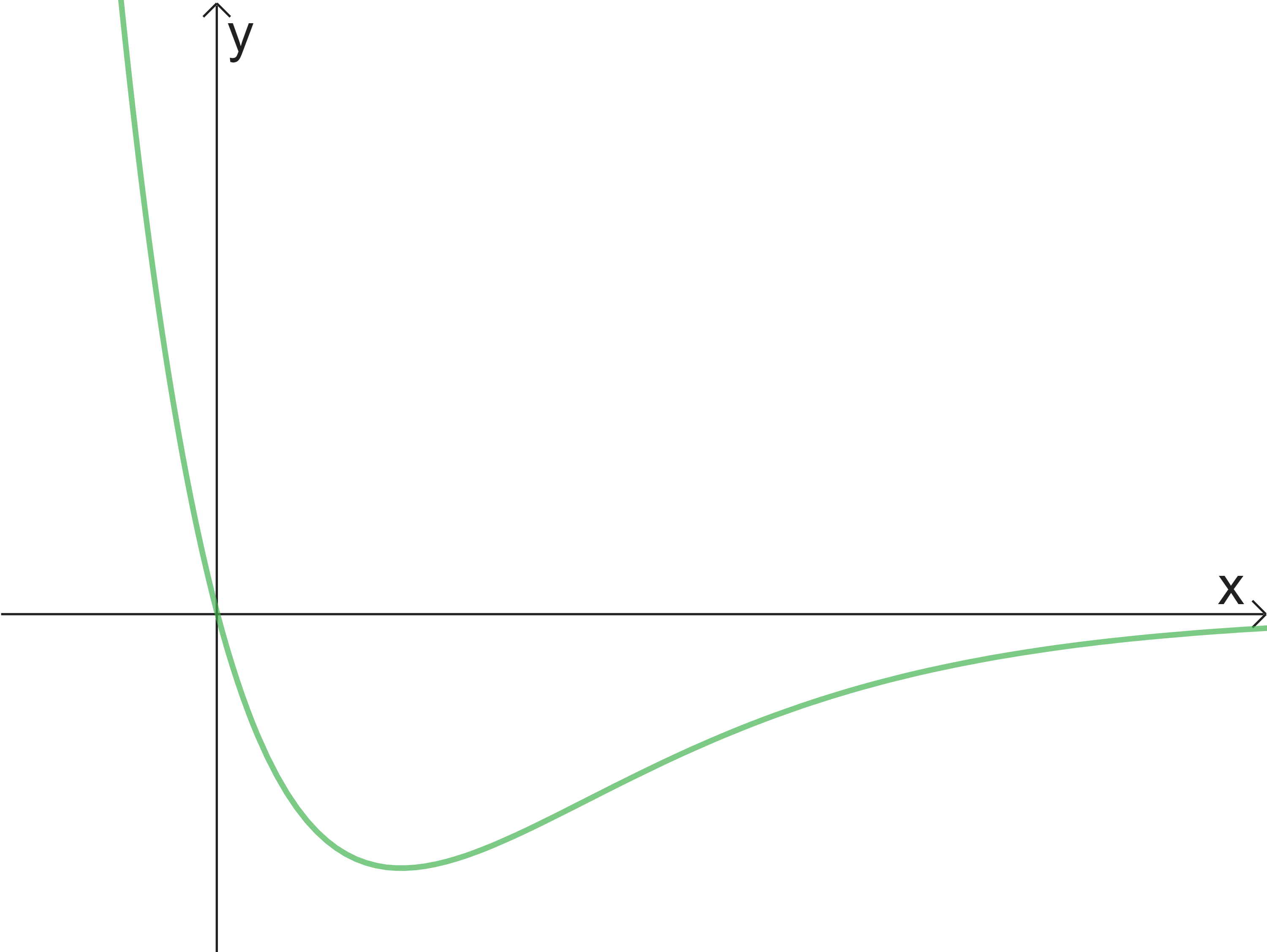
Analysis 2.2 - Flugzeugflügel

Gegeben sind die in $\mathbb{R}$ definierten Funktionen $f$ mit $f(x)= \left(-\frac{1}{10}x^2+2x\right)\cdot \mathrm e^{-0,1x}$ und $h$ mit $h(x ) = -\frac{3}{4}x\cdot \mathrm e^{-0,1x}.$
Der Graph von $f$ wird mit $G$ bezeichnet und der Graph von $h$ mit $H.$

Berechne die Koordinaten der Schnittpunkte von $G$ mit den Koordinatenachsen.

(4 BE)

Gib das Verhalten der Funktionswerte von $f$ für $x \rightarrow +\infty$ und $x \rightarrow -\infty$ an.

(2 BE)

Zeige, dass die Graphen $G$ und $H$ den gemeinsamen Punkt $S_1(0\mid 0)$ haben.

(1 BE)

Bestimme die Koordinaten und die Art der lokalen Extrempunkte von $G .$
Ohne Nachweis darfst du verwenden: $\(f$

(6 BE)

Die Funktion $h$ besitzt folgende Eigenschaften:

$\lim\limits_{x\to +\infty}h(x)=0;$ $\lim\limits_{x\to -\infty}h(x)= +\infty$
$\(h$

Begründe mithilfe einer Skizze, dass der Graph $H$ einen Wendepunkt besitzt.

(3 BE)

An den Graphen $H$ wird im Schnittpunkt mit der $x$ -Achse eine Tangente $t$ gelegt.
Die Tangente $t$ schließt mit der $x$ -Achse und der senkrechten Geraden $x =b$ mit $b \in \mathbb{R},$ $b\gt 0$ eine Fläche von $A= \frac{75}{2}\,\text{FE}$ ein.
Bestimme $b.$

(5 BE)

Die Konstrukteure einer kleinen Firma haben einen neuartigen Flugzeugflügel entworfen. Dabei werden die Graphen der Funktionen $f$ und $h$ zwischen ihren Schnittpunkten $S_1$ und $S_2$ zur Modellierung des Querschnitts dieses Flugzeugflügels verwendet (vgl. Abbildung 1).
Es gilt: $1\,\text{LE} = 1\,\text{dm}.$

Diagramm zur Darstellung der Länge von Flugzeugflügeln mit Verbindungslinien zwischen Punkten.

Abb. 1

Die Länge des Flugzeugflügels ist der horizontale Abstand zwischen $S_1$ und $S_2 .$
Zeige, dass diese Länge $27,5\,\text{dm}$ beträgt.

(4 BE)

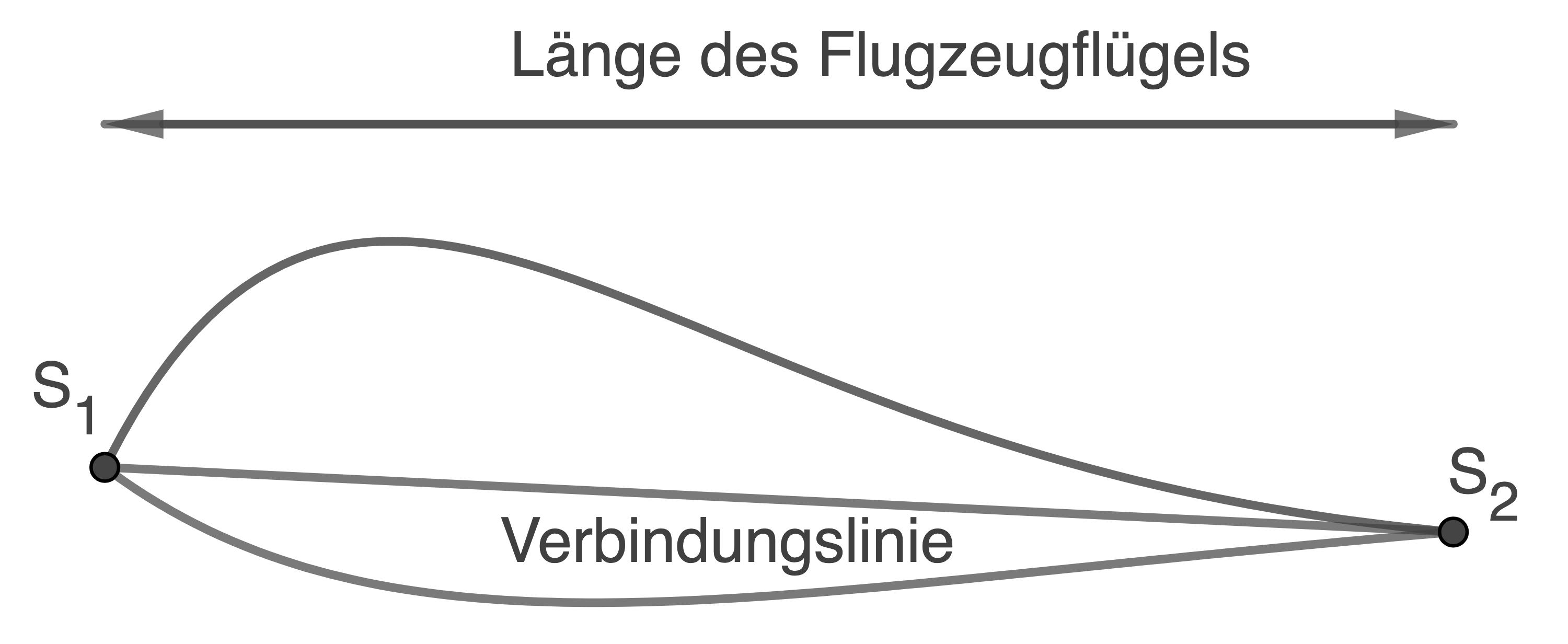
Begründe unter Zuhilfenahme der Abbildung 2 ohne Rechnung, dass die Länge des Flugzeugflügels kürzer als die Verbindungslinie zwischen $S_1$ und $S_2$ ist.

Diagramm mit zwei Punkten S1 und S2 auf einer Linie, die durch eine Verbindungslinie dargestellt werden.

Abb. 2

(2 BE)

An einer Stelle hat der Flugzeugflügel eine maximale vertikale Höhe. Diese Stelle kann mithilfe der Differenzfunktion $d$ mit $d(x) = f(x) - h(x)$ bestimmt werden. Die maximale vertikale Höhe darf $7,15\,\text{dm}$ nicht überschreiten.
Untersuche, ob die Konstrukteure dies beachtet haben.

(7 BE)

Bestimme die Querschnittsfläche des Flugzeugflügels mithilfe der Differenzfunktion $d.$
Ohne Nachweis darfst du verwenden, dass $D$ mit $D(x) = \left(x^2 -\frac{15}{2}x -75 \right)\cdot \mathrm e^{-0,1x}$ eine Stammfunktion von $d$ ist.

(2 BE)

Die Konstrukteure des Flügels benötigen den Neigungswinkel zwischen der Verbindungslinie $\overline{S_1S_2}$ und der Horizontalen und führen hierzu folgende Berechnungen durch:

(1)

$f(27,5) \approx 1,32$

(2)

$\sin \alpha = \frac{1,32}{\sqrt{27,5^2 -1,32^2}} \Leftrightarrow \alpha \approx 2,75 ^{\circ}$

Beurteile jeweils die einzelnen Teilschritte und beschreibe gegebenenfalls, wie fehlerhafte Schritte bei diesem Vorgehen berichtigt werden müssen.

(3 BE)

Die Richtung, aus der während einer bestimmten Phase des Fluges die Luft anströmt, kann modellhaft durch eine Gerade zwischen $S_1$ und einem Punkt $R(x_R \mid f(x_R))$ mit $x_R \lt 20$ angenommen werden. Im Punkt $R$ ändert der Graph von $f$ seine Krümmungsart.
Weise nach, dass die Größe des Winkels $\delta = \sphericalangle S_2S_1R$ nicht mehr als $18^{\circ}$ beträgt.

(zur Kontrolle: $R(12,68 \mid 2,61)$ )

(6 BE)

(45 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\begin{array}[t]{rll} f(x)&=&0\\ \left(-\frac{1}{10}x^2+2x\right)\cdot e^{-0,1x}&=&0\\ -\frac{1}{10}x^2+2x&=&0\\ x\cdot\left(-\frac{1}{10}x+2\right)&=&0\\ \end{array}$

Mit dem Satz vom Nullprodukt folgt $x_1=0$ und $x_2=20.$ Damit sind die Schnittpunkte mit der $x$ -Achse $N_1\left(0\mid0\right)$ und $N_2\left(20\mid0\right)$ . Im Punkt $N_1$ schneidet $G$ außerdem die $y$ -Achse.

$\lim\limits_{x\to+\infty} f(x)=0$

$\lim\limits_{x\to-\infty} f(x)=-\infty$

Aus Aufgabenteil a) ist $f(0)=0$ bekannt.

$h(0)=-\frac{3}{4}\cdot 0\cdot e^0=0$

Es gilt also $h(0)=0=f(0).$ Damit ist $S_1\left(0\mid0\right)$ ein gemeinsamer Punkt von $G$ und $H.$

Für das notwendige Kriterium für Extremstellen wird die erste Ableitung benötigt. Mit der Produktregel folgt:

Vollständigen Rechenweg anzeigen

$\( f$

Gleichsetzen:

Vollständigen Rechenweg anzeigen

$\(\begin{array}[t]{rll} f$

$f$ besitzt also zwei mögliche Extremstellen bei $x_1\approx5,86$ und $x_2\approx34,14.$

Mit dem hinreichenden Kriterium für Extremstellen lässt sich die Art der Extrema bestimmen:

$\(f$

Der Graph von $f$ hat einen Tiefpunkt $T\left(34,14\mid-1,59\right)$ und einen Hochpunkt $H\left(5,86\mid4,61\right).$

Graph einer mathematischen Funktion mit Achsenbeschriftungen x und y.

Für $x \lt 0$ verläuft der Graph $H$ im II. Quadranten. Er schneidet die $x$ -Achse im Koordinatenursprung und hat einen Tiefpunkt, der im IV. Quadranten liegt. Wegen $\lim\limits_{x\to+\infty}h(x) =0$ muss der Graph $H$ einen Wendepunkt haben.

1. Tangentengleichung aufstellen

Aus c) ist bekannt, dass $H$ die $x$ -Achse im Koordinatenursprung schneidet.

Mit der Produktregel folgt für die erste Ableitung von $h:$

Vollständigen Rechenweg anzeigen

$\( h$

Für die Steigung der Tangente an $H$ in diesem Punkt folgt:

$\(m = h$

Da die Tangente durch den Koordinatenursprung verläuft folgt:

$t(x)=-\frac{3}{4}x$

2. $b$ bestimmen

Die Tangete $t$ und die Gerade $x=b$ bilden mit der $x$ -Achse ein rechtwinkliges Dreieck.

$\begin{array}[t]{rll} A&=&\mid \frac{1}{2}\cdot x\cdot t(x)\mid\\ \frac{75}{2}&=&\mid \frac{1}{2}\cdot b\cdot \left(-\frac{3}{4}b\right)\mid\\ \frac{75}{2}&=&\mid-\frac{3}{8}\cdot b^2\mid\\ \frac{75}{2}&=& \frac{3}{8}\cdot b^2 & \quad \scriptsize \mid \;\cdot \frac{8}{3} \\ 100 &=& \frac{3}{8}\cdot b^2 \\ \pm 10 &=& b \end{array}$

Da $b\gt 0$ vorgegeben ist, ist $b=10.$

$S_1$ und $S_2$ sind die Schnittpunkte von $G$ und $H.$

Vollständigen Rechenweg anzeigen

$\begin{array}[t]{rll} f(x)&=& h(x)\\[5pt] ...& & \\[5pt] x\cdot \left(x-\frac{55}{2}\right) &=& 0 \\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt folgt $x_1= 0$ und $x_2= \frac{55}{2} = 27,5.$

Die Länge des Flugzeugflügels beträgt also $27,5\text{ LE}.$

Die Verbindungslinie zwischen $S_1$ und $S_2$ entspricht der Hypotenuse des rechtwinkligen Dreiecks in der Abbildung. Da die Hypotenuse in einem rechtwinkligen Dreieck immer die längste Seite ist, ist die Verbindungslinie länger als die Länge des Flugzeugflügels, der hier einer der Katheten entspricht.

1. Funktion und Ableitung bestimmen

Mit der Produktregel folgt für die erste Ableitung von $d:$

Vollständigen Rechenweg anzeigen

$\(\begin{array}[t]{rll} d(x) &=& f(x) -h(x) \\[5pt] &=& \left(-\frac{1}{10}x^2+\frac{11}{4}x\right)\cdot e^{-0,1x} \\[5pt] d$

2. Notwendiges Kriterium für Extremstellen

Vollständigen Rechenweg anzeigen

$\(\begin{array}[t]{rll} d$

Mit der pq-Formel folgt $x_1\approx6,75$ und $x_2\approx40,75.$ Dabei entfällt die zweite Lösung $x_2.$

3. Maximale vertikale Höhe

$d(x_1)\approx d(6,75)$ $=\left(-\frac{1}{10}\cdot(6,75)^2+\frac{11}{4}\cdot6,75\right)\cdot e^{-0,1\cdot6,75}$ $\approx7,13\lt7,15$

Die maximale Höhe beträgt $7,13\text{ dm}$ . Die Konstrukteure haben die maximale Höhe beachtet.

$\begin{array}[t]{rll} A&=&\displaystyle\int_{0}^{27,5}d(x)\;\mathrm dx\\ &=&\left[D(x)\right]_0^{27,5}\\ &=&D(27,5)-D(0)\\ &\approx&105,37\text{ FE}=105,37\text{ dm}^2 \end{array}$

Die Querschnittsfläche des Flugzeugflügels beträgt ca. $105,37\text{ dm}^2$ .

Die Konstrukteure berechnen den Neigungswinkel aus der Verbindungslinie $\overline{S_1S_2}$ und der Horizontalen $f(27,5)$ mithilfe des Sinus.

Im ersten Teilschritt wurde der Wert für $f(27,5)$ falsch berechnet bzw. das Vorzeichen ist falsch: $f(27,5)=-1,32$

Hier wurde die Hypotenuse $\overline{S_1S_2}$ falsch berechnet, da $\overline{S_1S_2}=\sqrt{27,5^2+1,32^2}$ . Die richtige Rechnung muss lauten:
$\sin(\alpha)$ $=\frac{\text{Gegenkathete}}{\text{Hypotenuse}}$ $=\frac{1,32}{\sqrt{27,5^2+1,32^2}}$

1. Punkt $R$ bestimmen

Da im Punkt $R$ der Graph seine Krümmungsart ändert, ist $R$ ein Wendepunkt des Graphen von $f.$ Es gilt also:

$\(\begin{array}[t]{rll} f$

Mit der pq-Formel folgt $x_1\approx12,68$ und $x_2\approx47,32.$ Die zweite Lösung $x_2$ entfällt.

Mit $f(12,68) \approx 2,61$ ist $R(12,68\mid 2,61).$

2. Winkel $\beta$ berechnen

Der Winkel $\beta$ spannt sich zwischen der $x$ -Achse und der Strecke vom Ursprung zum Punkt $R.$ $\beta$ lässt sich mithilfe des Tangens berechnen:

$\tan(\beta)=\frac{\Delta y}{\Delta x}=\frac{2,61}{12,68}$

$\beta = \tan^{-1}\left(\frac{2,61}{12,68}\right) \approx 11,63\,^\circ$

3. Winkel $\delta$ berechnen

Der Winkel $\delta=\measuredangle S_2S_1R$ berechnet sich aus dem Winkel $\alpha$ (siehe Aufgabenteil k) und dem Winkel $\beta$ des Punkts $R.$

$\delta$ $=\alpha+\beta$ $=2,75\,^\circ+11,63\,^\circ$ $=14,38\,^\circ$ $\leq18\,^\circ$

Damit beträgt der Winkel $\delta=14,38\,^\circ$ und ist kleiner als $18\,^\circ$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?