Analysis 2.1 - Tauchroboter
1
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  . Für die erste Ableitungsfunktion von
. Für die erste Ableitungsfunktion von  gilt
gilt  .
.
a)
Gib die Koordinaten der Schnittpunkte des Graphen von  mit den Koordinatenachsen an. Begründe, dass der Graph von
mit den Koordinatenachsen an. Begründe, dass der Graph von  einen Hochpunkt hat, und gib die Koordinaten dieses Hochpunkts an.
einen Hochpunkt hat, und gib die Koordinaten dieses Hochpunkts an.
(5 BE)
b)
Gib den Grenzwert von  für
für  an und beschreibe den Verlauf des Graphen von
an und beschreibe den Verlauf des Graphen von  für
für  .
.
(2 BE)
c)
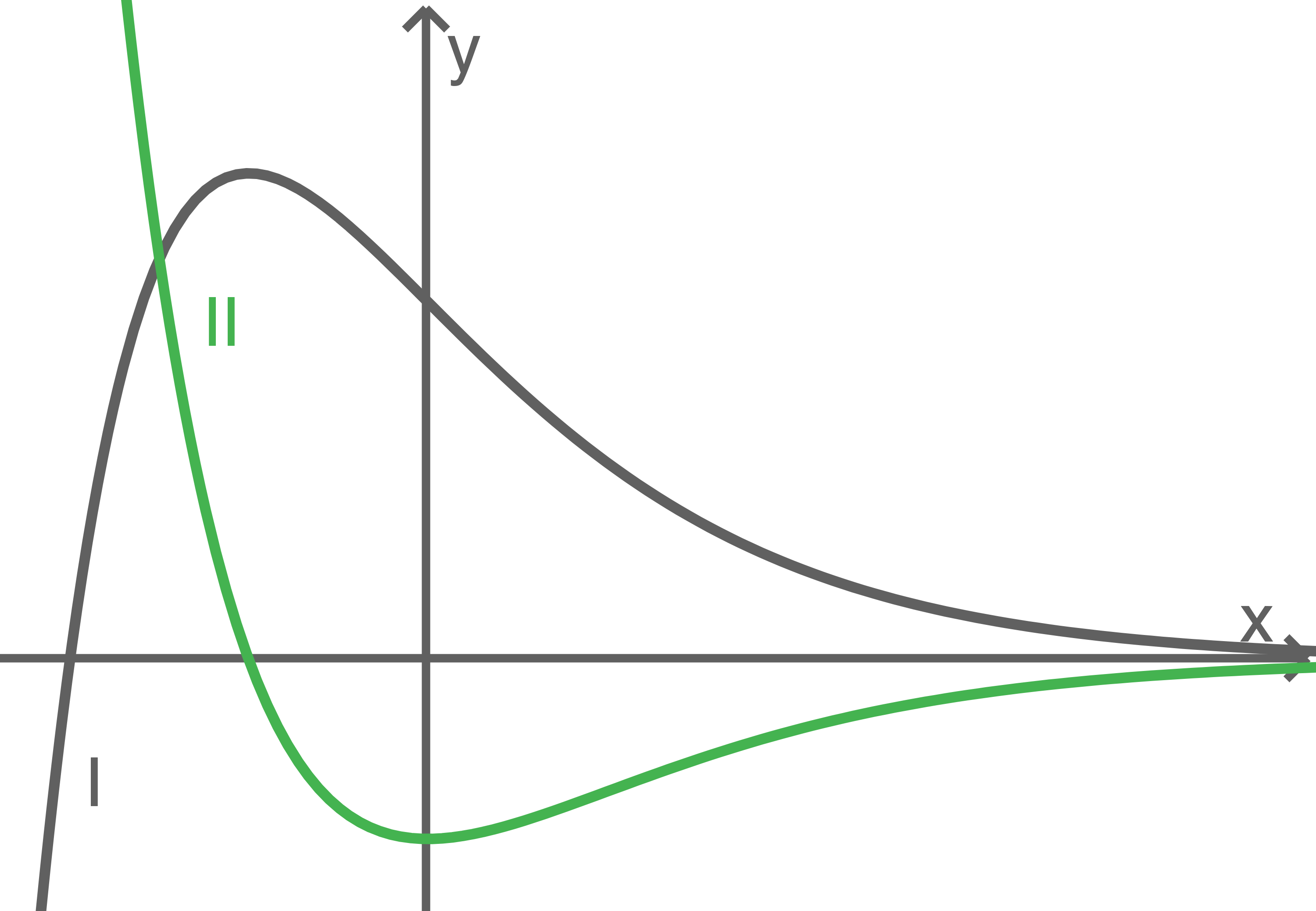
Die Abbildung zeigt die Graphen der Funktion  und der zugehörigen Ableitungsfunktion
und der zugehörigen Ableitungsfunktion  . Entscheide, welcher der Graphen I und II die Ableitungsfunktion
. Entscheide, welcher der Graphen I und II die Ableitungsfunktion  darstellt. Begründe deine Entscheidung.
darstellt. Begründe deine Entscheidung.

(2 BE)
d)
Weise nach, dass der Schnittpunkt der Graphen von  und
und  bei
bei  liegt.
liegt.
(2 BE)
e)
Ermittle den Winkel, unter dem sich die Graphen von  und
und  schneiden.
schneiden.
(4 BE)
f)
Begründe ohne Rechnung, dass gilt  .
.
(3 BE)
g)
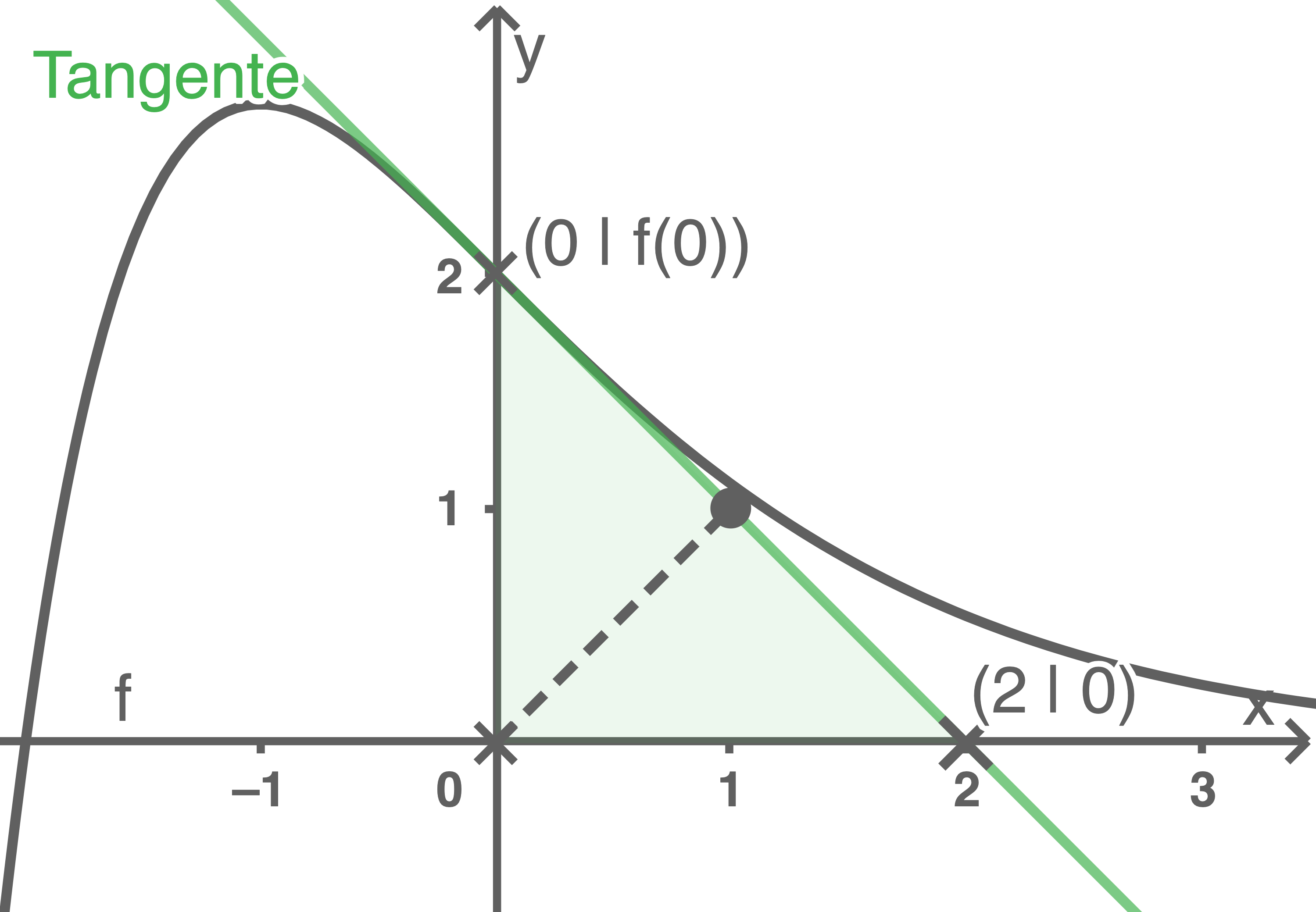
Die Tangente an den Graphen von  im Punkt
im Punkt  schließt mit den Koordinatenachsen ein Dreieck ein. Berechne den Umfang dieses Dreiecks und gib die Koordinaten des Punkts an, der von allen Eckpunkten des Dreiecks den gleichen Abstand hat.
schließt mit den Koordinatenachsen ein Dreieck ein. Berechne den Umfang dieses Dreiecks und gib die Koordinaten des Punkts an, der von allen Eckpunkten des Dreiecks den gleichen Abstand hat.
(5 BE)
h)
Der Koordinatenursprung und ein auf dem Graphen von  liegender Punkt
liegender Punkt  mit
mit  sind gegenüberliegende Eckpunkte eines achsenparallelen Rechtecks. Für genau einen Wert
sind gegenüberliegende Eckpunkte eines achsenparallelen Rechtecks. Für genau einen Wert  hat das Rechteck eine maximale Fläche. Ermittle für diesen Fall die Koordinaten des Punkts
hat das Rechteck eine maximale Fläche. Ermittle für diesen Fall die Koordinaten des Punkts  .
.
 Zur Kontrolle:
Zur Kontrolle: 

(5 BE)
i)
Im 4. Quadranten schließen der Graph von  , die beiden Koordinatenachsen und die Gerade
, die beiden Koordinatenachsen und die Gerade  eine Fläche
eine Fläche  ein.
ein.
Begründe, dass es einen Wert für gibt, so dass der Flächeninhalt der Fläche
gibt, so dass der Flächeninhalt der Fläche  genau
genau  beträgt.
beträgt.
Begründe, dass es einen Wert für
(4 BE)
2
Ein Tauchroboter bewegt sich in vertikaler Richtung. Diese Bewegung lässt sich für  modellhaft mithilfe der in
modellhaft mithilfe der in  definierten Funktion
definierten Funktion
 beschreiben. Dabei ist
beschreiben. Dabei ist  die seit Beobachtungsbeginn vergangene Zeit in Minuten und
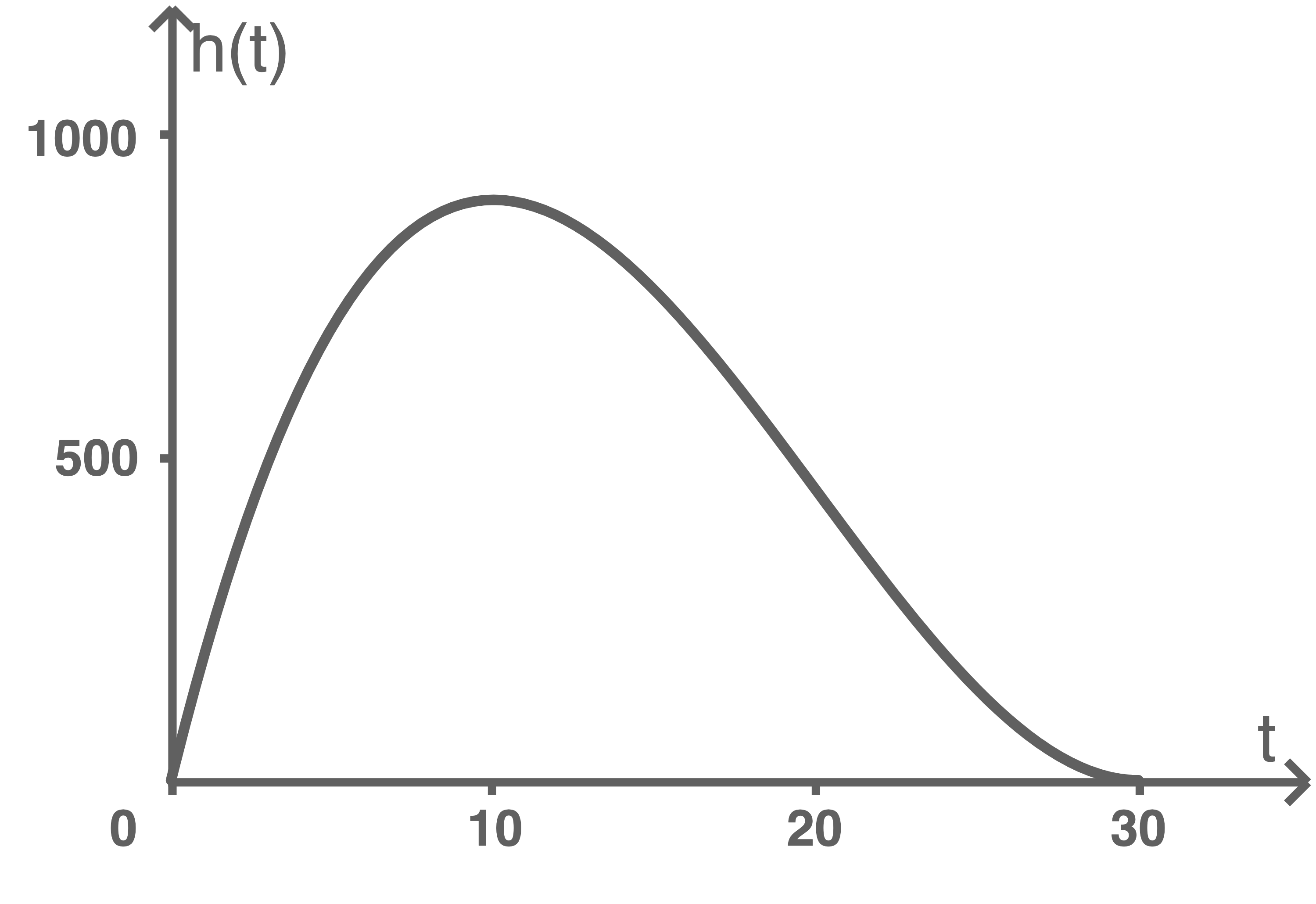
die seit Beobachtungsbeginn vergangene Zeit in Minuten und  der Abstand des Roboters von der Wasseroberfläche in Metern. Die Abbildung stellt die Bewegung des Roboters dar.
der Abstand des Roboters von der Wasseroberfläche in Metern. Die Abbildung stellt die Bewegung des Roboters dar.
a)
Weise nach, dass der Roboter zum Zeitpunkt 10 Minuten nach Beobachtungsbeginn den größten Abstand zur Wasseroberfläche hat und dass dieser Abstand 900 Meter beträgt.
(3 BE)
b)
Berechne, wie viele Meter der Roboter innerhalb der ersten 15 Minuten nach Beobachtungsbeginn zurücklegt.
(3 BE)
c)
Beschreibe die Bedeutung des Wendepunkts des Graphen von  im Hinblick auf die Bewegung des Roboters.
im Hinblick auf die Bewegung des Roboters.
(2 BE)
d)
Betrachtet wird die Phase, in der der Roboter seinen Abstand zur Wasseroberfläche vergrößert. Berechne den Zeitraum innerhalb dieser Phase, in dem die Geschwindigkeit des Roboters mindestens 29,7 Meter pro Minute ist.
(5 BE)
(45 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Koordinaten der Schnittpunkte des Graphen von  mit den Koordinatenachsen
mit den Koordinatenachsen
![\(\begin{array}[t]{rll}
f(x)&=& 0 \\[5pt]
(x+2) \cdot \mathrm e^{-x}&=& 0
\end{array}\)](https://mathjax.schullv.de/f31ead0d87093eac19c630c44cd20db20b97e27cd9c741d45de56153ac837d54?color=5a5a5a) Anwenden des Satzes vom Nullprodukt:
Anwenden des Satzes vom Nullprodukt:
Für ergibt sich
ergibt sich  Für
Für  gibt es keine Lösung. Somit ergeben sich die Koordinaten des Schnittpunkts mit der
gibt es keine Lösung. Somit ergeben sich die Koordinaten des Schnittpunkts mit der  -Achse mit
-Achse mit 
![\(\begin{array}[t]{rll}
f(0)&=&(0+2)+\mathrm e^{0} \\[5pt]
&=& 2
\end{array}\)](https://mathjax.schullv.de/fc04c8a6722986fe78be3d8d7751990d168e2b40aab6980080ff14c83b0014ff?color=5a5a5a) Die Koordinaten des Schnittpunkts mit der
Die Koordinaten des Schnittpunkts mit der  -Achse ergeben sich mit
-Achse ergeben sich mit  Koordinaten des Hochpunkts bestimmen
Es gilt:
Koordinaten des Hochpunkts bestimmen
Es gilt:  Anwendung der Produkt- und Kettenregel:
Anwendung der Produkt- und Kettenregel:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/2d80a929f2962117e3712bdc1870e7ca47507eab0a4e7c09bd27417d7e99de6b?color=5a5a5a) 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/c68f42207d3ee45ae7d0be251520606829c1ec883fa941572adc715165e09390?color=5a5a5a) Anwenden des Satzes vom Nullprodukt: Für
Anwenden des Satzes vom Nullprodukt: Für  ergibt sich
ergibt sich  Für
Für  gibt es keine Lösung.
2. Schritt: Hinreichende Bedingung für Extremstellen
gibt es keine Lösung.
2. Schritt: Hinreichende Bedingung für Extremstellen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/c5380f49cedabb3e06c7e7ca9b72fb4c8e8dc8c54bd38b9fde330e86d856888f?color=5a5a5a) Somit ist gezeigt, dass sich an der Stelle
Somit ist gezeigt, dass sich an der Stelle  ein Hochpunkt befindet.
ein Hochpunkt befindet.

 Die Koordinaten des Hochpunktes ergeben sich somit mit
Die Koordinaten des Hochpunktes ergeben sich somit mit 
Für
b)
c)
Graph II stellt den Graphen der Ableitungsfunktion dar.
Begründung: Der Graph II schneidet die  -Achse im Punkt
-Achse im Punkt  Der Extrempunkt des Graphen I hat die Koordinaten
Der Extrempunkt des Graphen I hat die Koordinaten  Es gilt
Es gilt  somit stellt Graph II die Ableitungsfunktion dar.
somit stellt Graph II die Ableitungsfunktion dar.
d)
e)
Es gilt: 






 Der Schnittwinkel, unter dem sich die Graphen von
Der Schnittwinkel, unter dem sich die Graphen von  und
und  schneiden ergibt sich mit:
schneiden ergibt sich mit:

f)
Die Funktion  ist im Intervall
ist im Intervall ![\([-3;- 2]\)](https://mathjax.schullv.de/73747e53f0d3c665b2354e17856f8ab5e225608172081bc9d0ee7605e2ed3335?color=5a5a5a) monoton steigend, d.h.
monoton steigend, d.h.  Also ist
Also ist  Der Graph der ersten Ableitungsfunktion
Der Graph der ersten Ableitungsfunktion  verläuft im Intervall
verläuft im Intervall ![\([-1; 0]\)](https://mathjax.schullv.de/2a23d9bb4360dfcc8b6f6be9c468f47e0bfae23900fc83f86d7d786b051cf01a?color=5a5a5a) unterhalb der
unterhalb der  -Achse, da die Funktion
-Achse, da die Funktion  in diesem Intervall monoton fallend ist.
Es gilt
in diesem Intervall monoton fallend ist.
Es gilt  Damit gilt
Damit gilt 
g)
Es ist  d.h. die Tangente schneidet die
d.h. die Tangente schneidet die  -Achse im Punkt
-Achse im Punkt  Damit beträgt der gesuchte Umfang
Damit beträgt der gesuchte Umfang  Koordinaten des gesuchten Punktes:
Koordinaten des gesuchten Punktes: 
h)
Für den Flächeninhalt des eingeschlossenen Rechtecks gilt:
![\(\begin{array}[t]{rll}
A(u) &=& u \cdot f(u) \\[5pt]
&=& u \cdot (u+2)\cdot \mathrm e^{-u} \\[5pt]
&=& (u^2+2u) \cdot \mathrm e^{-u}
\end{array}\)](https://mathjax.schullv.de/9e46d3fefed227aa1c0bf4a6b721f6daceb53aa89f7a9e34964f6d709534834c?color=5a5a5a) Um den maximalen Flächeninhalt des Rechtecks zu bestimmen, wird
Um den maximalen Flächeninhalt des Rechtecks zu bestimmen, wird  auf Maximalstellen überprüft. Anwendung der Ketten- und Produktregel ergibt:
auf Maximalstellen überprüft. Anwendung der Ketten- und Produktregel ergibt:



 Notwendige Bedingung für Extremstellen anwenden
Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
A](https://mathjax.schullv.de/d97eaecb09d562ddb5bb0a0a9fb3d518e75e4bd6cc09f3d8e5ab6d059a61862c?color=5a5a5a) Anwenden des Satzes vom Nullprodukt: Für
Anwenden des Satzes vom Nullprodukt: Für  ergibt sich
ergibt sich  da
da  Für
Für  gibt es keine Lösung.
Hinreichende Bedingung für Extremstellen anwenden
gibt es keine Lösung.
Hinreichende Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
A](https://mathjax.schullv.de/236df2d35c8dfdf7fa5ed0ca731a9feb6eca7b6435658cfaee75d1a229036f11?color=5a5a5a) Es handelt sich somit um eine Maximalstelle.
Es handelt sich somit um eine Maximalstelle.
 Daraus folgen die Koordinaten mit
Daraus folgen die Koordinaten mit 
i)
2
a)
Es muss überprüft werden, ob an der Stelle  eine Maximalstelle vorliegt.
eine Maximalstelle vorliegt.


 In Verbindung mit der Abbildung ergibt sich, dass
In Verbindung mit der Abbildung ergibt sich, dass  für
für  bei 10 sein Maximum annimmt.
bei 10 sein Maximum annimmt.

b)
Der Roboter legt in den ersten 10 Minuten eine Strecke von  zurück.
Diese gleiche Strecke müsste der Roboter wieder zurücklegen um zum Zeitpunkt
zurück.
Diese gleiche Strecke müsste der Roboter wieder zurücklegen um zum Zeitpunkt  wieder an der Wasseroberfläche zu sein.
Zum Zeitpunkt
wieder an der Wasseroberfläche zu sein.
Zum Zeitpunkt  hat der Roboter einen Abstand von
hat der Roboter einen Abstand von  Metern zur Wasseroberfläche. das heißt er legt in
Metern zur Wasseroberfläche. das heißt er legt in ![\([10; 15]\)](https://mathjax.schullv.de/84ef120b76aacc07dc3d75ac77dfaa9c82f227987b3b42df20fc385c872dfe9a?color=5a5a5a) eine Strecke von
eine Strecke von  zurück.
zurück.
 d. h. der Roboter legt etwa 1041 Meter zurück.
d. h. der Roboter legt etwa 1041 Meter zurück.
c)
Die  -Koordinate des Wendepunkts gibt den Zeitpunkt an, zu dem der Roboter während des Aufsteigens die größte Geschwindigkeit hat.
-Koordinate des Wendepunkts gibt den Zeitpunkt an, zu dem der Roboter während des Aufsteigens die größte Geschwindigkeit hat.
d)