Analysis 2.1 - Beistelltisch
Gegeben ist die in 
definierte Funktion 
mit 
Der Graph der Funktion wird mit 
bezeichnet.
Für die erste Ableitungsfunktion
von gilt 
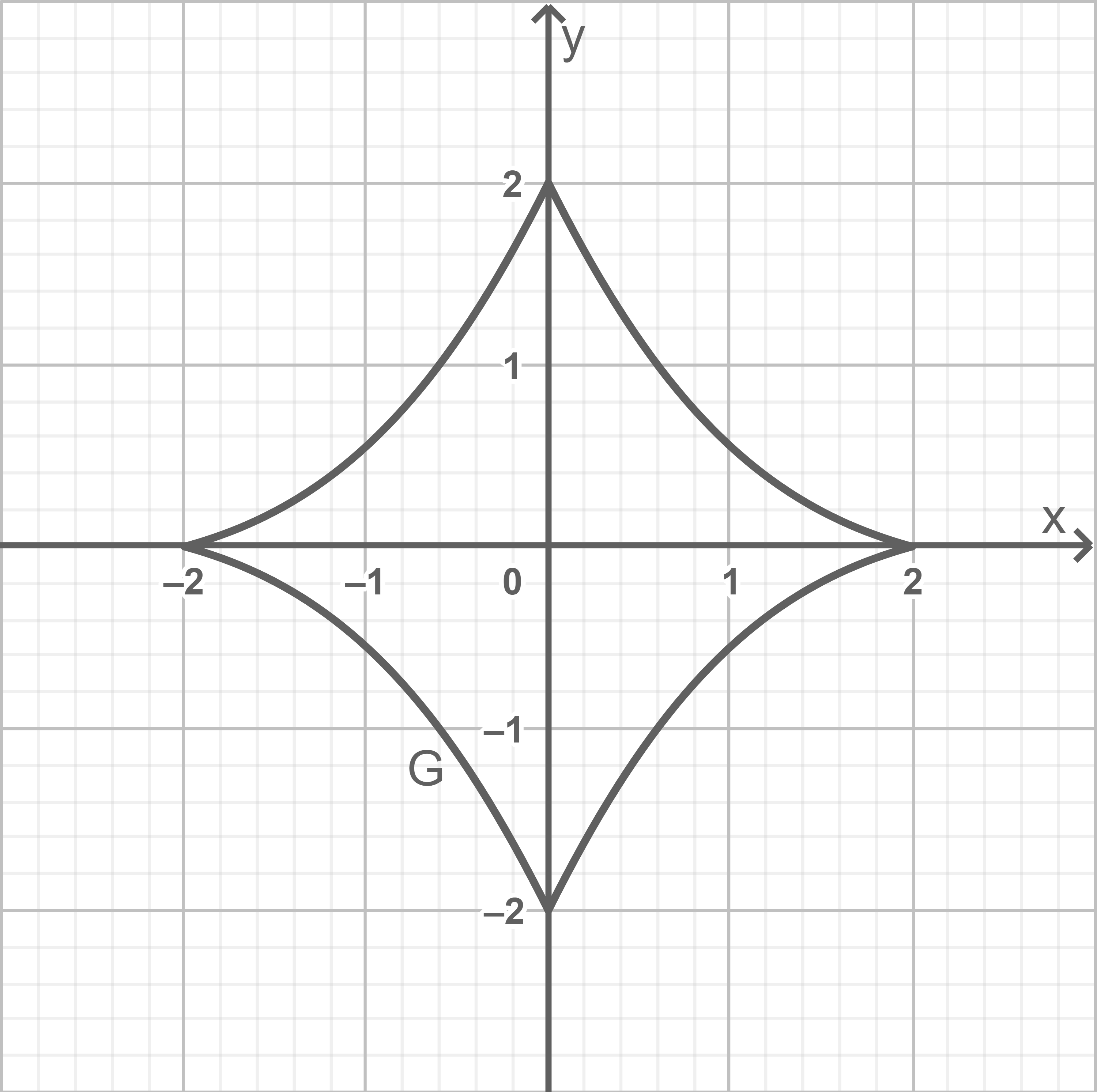
Der Graph der Funktion
Für die erste Ableitungsfunktion
a)
Gib das Verhalten der Funktionswerte von für 
und 
an.
(2 BE)
b)
Bestimme die Koordinaten der Schnittpunkte von mit den beiden Koordinatenachsen. Ein Punkt 
und die drei Schnittpunkte sind die Eckpunkte einer Raute. Gib die Koordinaten des Punktes an.
(5 BE)
c)
Zeige, dass der Graph an der Stelle 
eine waagerechte Tangente besitzt. Berechne den Funktionswert an dieser Stelle.
(2 BE)
d)
Der Graph hat genau zwei lokale Extrempunkte, von denen einer im II. und einer im IV. Quadranten liegt. Der Punkt 
ist der Tiefpunkte von 
Entscheide ohne weitere Rechnung, ob die folgenden Aussagen wahr sind.
Begründe deine Entscheidung.
ist kleiner als die 
-Koordinate des Tiefpunktes.
ist größer als null.
Begründe deine Entscheidung.
(4 BE)
e)
Gib das Monotonieverhalten von für 
an.
(2 BE)
f)
Der Graph besitzt zwei Wendepunkte. Berechne die Koordinaten beider Wendepunkte auf zwei Nachkommastellen gerundet.
(5 BE)
g)
Die Abbildung 1 zeigt einen Teil des Graphen Die Tangente an im Wendepunkt 
begrenzt mit den Koordinatenachsen ein Dreieck. Die zu dieser Tangente senkrechte Gerade durch den Punkt begrenzt mit den Koordinatenachsen ein weiteres Dreieck.
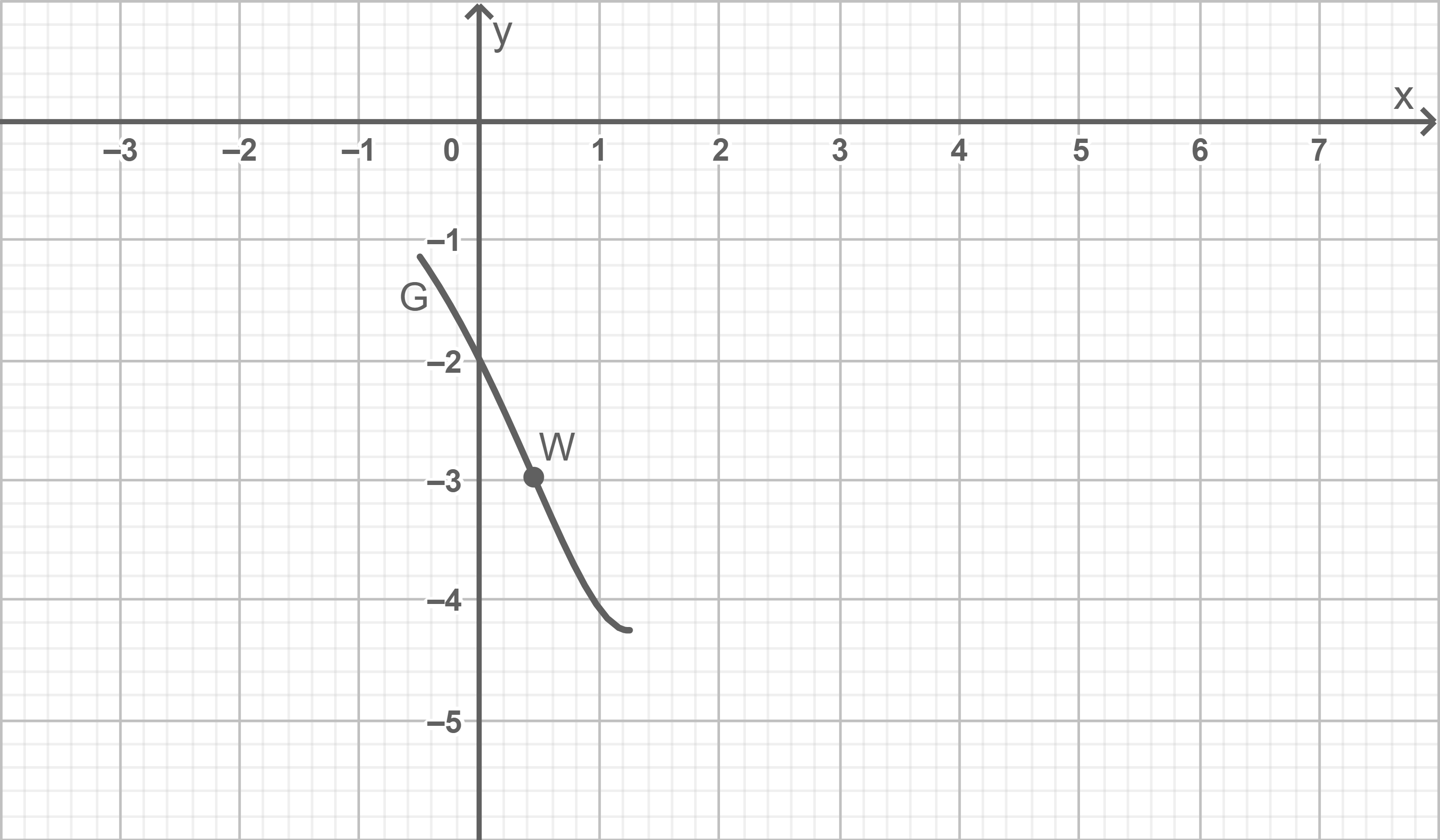Zeichne in die Abbildung 1 beide Dreiecke ein. Begründe mithilfe der Zeichnung, dass das eine Dreieck eine maßstäbliche Vergrößerung des anderen Dreiecks ist.
Abb. 1
(5 BE)
h)
Es gibt 
für die gilt: 
. Erläutere die geometrische Bedeutung dieser Gleichung.
(2 BE)
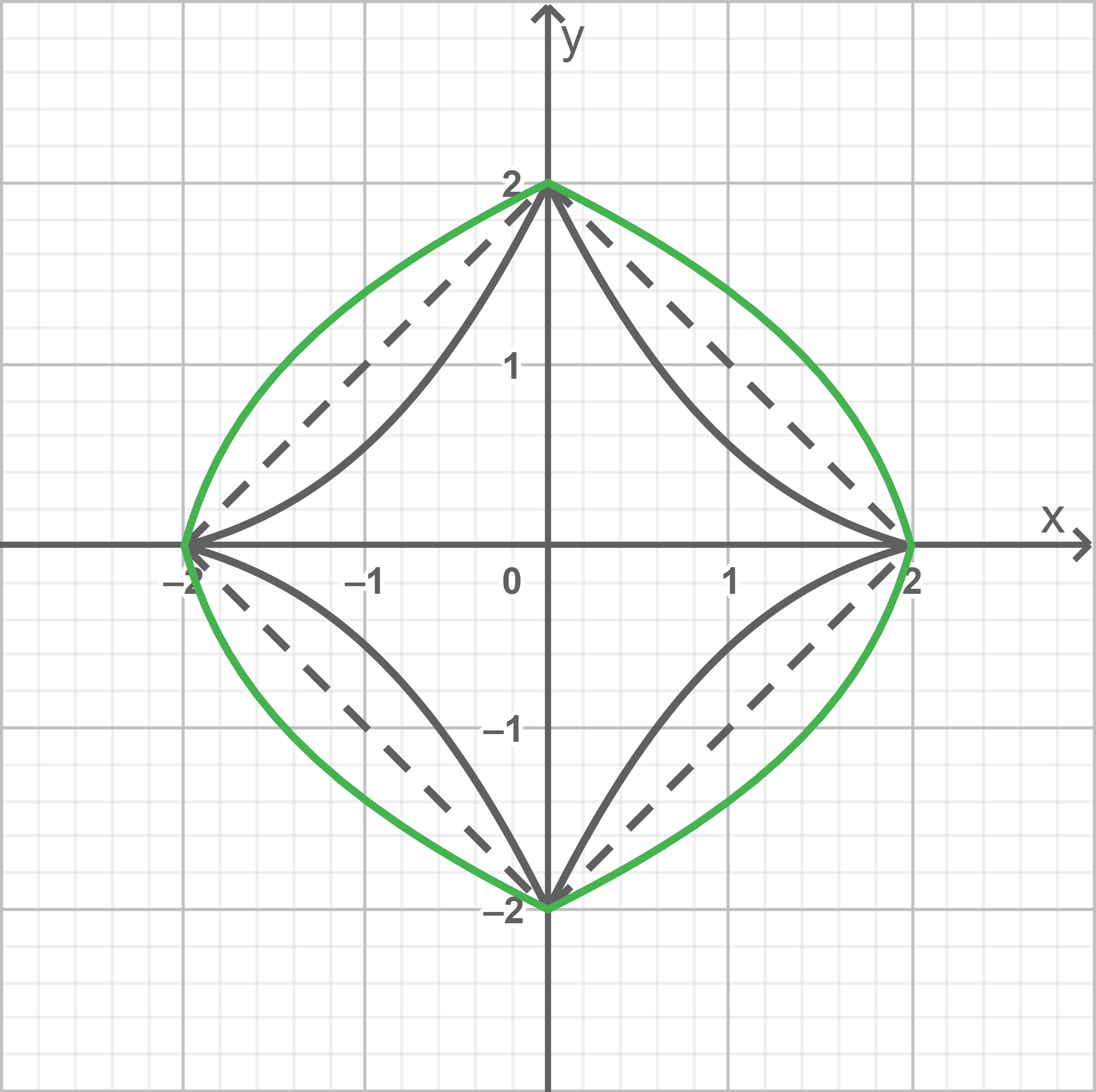
Ein Möbeldesigner hat sich auf die Herstellung kleiner Beistelltische spezialisiert. Die Abbildung 2 zeigt modellhaft die Draufsicht einer symmetrischen Tischplatte.
Zur Modellierung einer der vier Randlinien der Tischplatte wurde der im III. Quadranten verlaufende Teil des Graphen der Funktion verwendet. Es gilt 
Zur Modellierung einer der vier Randlinien der Tischplatte wurde der im III. Quadranten verlaufende Teil des Graphen der Funktion
Abb. 2
i)
Im I., II. und IV. Quadranten werden die Randlinien der Tischplatte durch Teile der Graphen der Funktion 
und 
beschrieben.
Gib die Funktionsgleichungen von zwei dieser Funktionen an.
Gib die Funktionsgleichungen von zwei dieser Funktionen an.
(2 BE)
j)
Berechne die Größe des Winkels, den die zwei Randlinien der Tischplatte im Punkt 
einschließen.
(3 BE)
k)
Der Beistelltisch hat eine Höhe von 
Metern und soll in einem quaderförmigen Karton mit quadratischer Grundfläche ausgeliefert werden.
Bestimme das Mindestvolumen des Kartons in Litern.
Bestimme das Mindestvolumen des Kartons in Litern.
(4 BE)
l)
Es gilt: 
Ermittle mithilfe dieser Gleichung eine Stammfunktion von.
Berechne den Flächeninhalt der Tischplatte und gib diesen in Quadratzentimetern an.
Für einen neuen Beistelltisch wird die bisherige Form der Tischplatte als Grundlage genutzt. Für die neue Tischplatte wird jede der vier Randlinien der ursprünglichen Tischplatte an der jeweiligen Geraden gespiegelt, die durch die Achsenschnittpunkte im entsprechenden Quadranten verläuft.
Ermittle mithilfe dieser Gleichung eine Stammfunktion von
Berechne den Flächeninhalt der Tischplatte und gib diesen in Quadratzentimetern an.
(5 BE)
m)
Skizziere in die Abbildung 2 die Randlinien der neuen Tischplatte. Der Flächeninhalt der neuen Tischplatte ist größer als der Flächeninhalt der ursprünglichen Tischplatte.
Beschreibe einen Lösungsweg, um diesen Größenunterschied zu ermitteln.
Beschreibe einen Lösungsweg, um diesen Größenunterschied zu ermitteln.
(4 BE)
(45 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Da 
schneller steigt bzw. fällt als der lineare Term in der Klammer, folgt:
b)
1. Schritt: Koordinaten der Schnittpunkte von G mit Koordinatenachsen
![\(\begin{array}[t]{rll}
f(x)&=&0 \\[5pt]
0,5\cdot(x^2-4)\cdot \mathrm e^x&=&0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/60547c232987a10495574936e9e571193d227c8ca6a348c4738c31c43e6c22ea?color=5a5a5a)
Da stets 
folgt mit dem Satz des Nullprodukts:
![\(\begin{array}[t]{rll}
0,5\cdot(x^2-4)&=&0 &\quad \scriptsize \mid\;:0,5 \\[5pt]
x^2-4&=&0 &\quad \scriptsize \mid\;+4 \\[5pt]
x^2&=&4 &\quad \scriptsize \mid\;\sqrt{\;} \\[5pt]
x_1&=& 2 \\[5pt]
x_2&=& -2
\end{array}\)](https://mathjax.schullv.de/1da17143d0d8c9d4f80dbe3a6db52fd18769937dd3479621b8e576c464a812f2?color=5a5a5a)
Die Koordinaten der Schnittpunkte von mit den Achsen sind also durch 
und 
gegeben.
2. Schritt: Koordinaten von angeben
Aus den Koordinaten der anderen drei Punkte kann abgelesen werden, dass der vierte Eckpunt der Raute die Koordinaten 
haben muss.
c)
Einsetzen von 
in 
liefert:
Somit ist die Tangente an den Graphen im Punkt 
waagerecht. Durch Einsetzen in 
folgt weiter:
d)
Laut Aufgabenstellung hat der Graph für nur den Extrempunkt 
Der gegebene 
-Wert 
ist größer als 
Es folgt:
Die Aussage ist falsch, da rechts vom Tiefpunkt alle -Koordinaten der Punkte des Graphen größer als die des Tiefpunktes sind.
Die Aussage ist wahr, weil der Graph rechts vom Tiefpunkt steigend verläuft.
e)
Mit Hilfe von Aufgabenteil d) folgt:
ist monoton fallend für 
und monoton wachsend für 
f)
1. Schritt: Zweite Ableitung berechnen
Mit der Produktregel folgt:
2. Schritt: Notwendige Bedingung
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/e26df054feb686e1508d189de223fb8a22684eb0ebec578acddc69930df15996?color=5a5a5a)
Da stets folgt mit dem Satz des Nullprodukts:
![\(\begin{array}[t]{rll}
0,5 x^2+2x-1&=&0 &\quad \scriptsize \mid\;:0,5 \\[5pt]
x^2+4x-2&=&0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/76ecdc3c7de3152659117be38ca9346b0084ec5efbbad6e68a69f60b11b33cea?color=5a5a5a)
Anwendung der 
-Formel liefert:
![\(\begin{array}[t]{rll}
x_{1;2}&=&-\dfrac{4}{2}\pm\sqrt{\left(\dfrac{4}{2}\right)^2+2} \\[5pt]
x_{1;2}&=&-2\pm\sqrt{6} \\[5pt]
x_1&\approx&0,45 \\[5pt]
x_2&\approx&-4,45
\end{array}\)](https://mathjax.schullv.de/7560bee1a569d4b305c2fd1ef0db70aebffa20f1ac04f4fce14b237d77777029?color=5a5a5a)
Da laut Aufgabenstellung zwei Wendestellen existieren, muss die hinreichende Bedingung nicht überprüft werden. Einsetzen von 
und 
in liefert:
Die Koordinaten der beiden Wendestellen sind somit ungefähr 
und 
g)
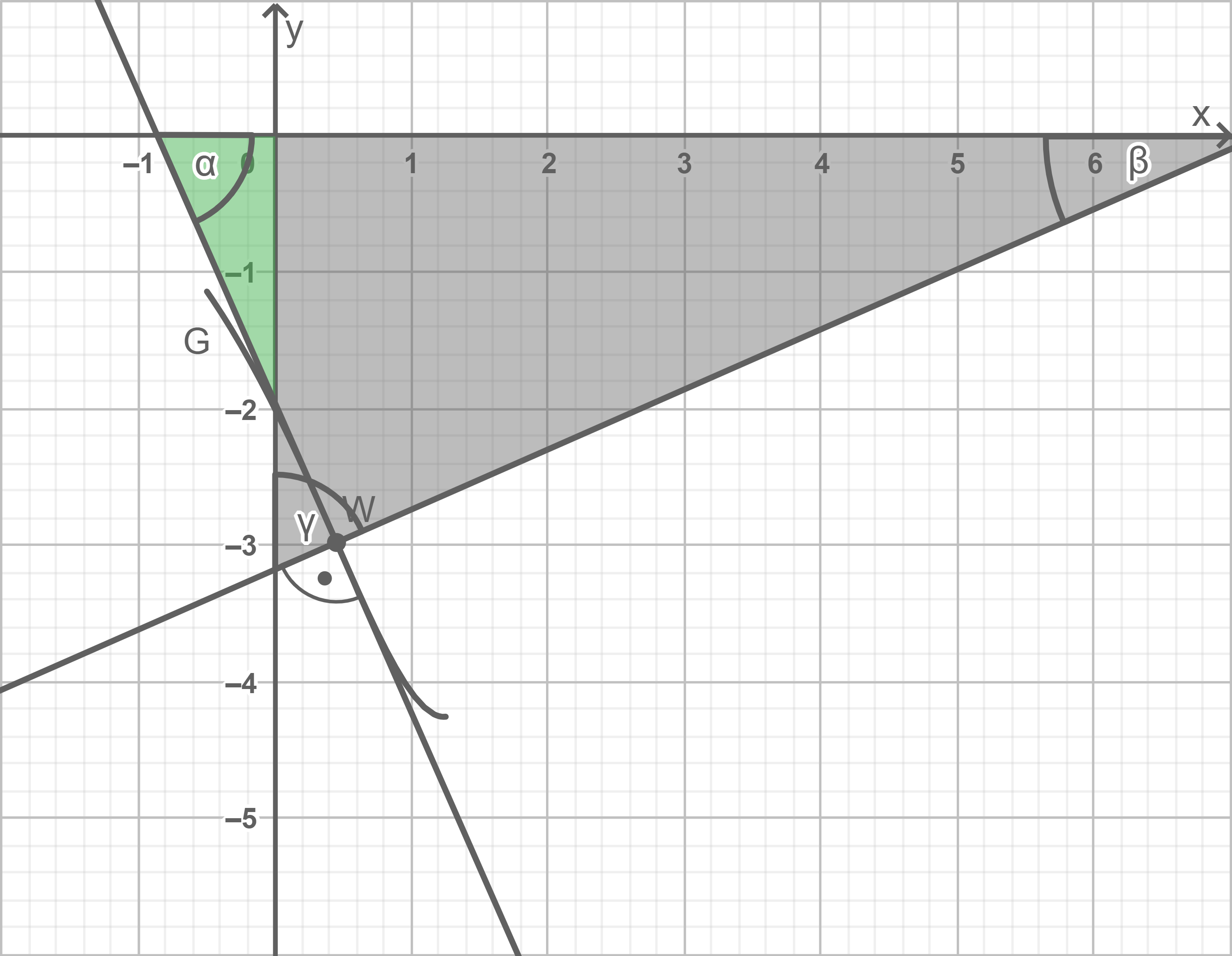
h)
Die Graphen der Funktionen und verlaufen senkrecht in den Punkten, für die diese Gleichung gilt.
i)
j)
Der halbe Winkel ergibt sich durch den Winkel 
zwischen dem Graphen von und der -Achse:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&f](https://mathjax.schullv.de/6f99792f002c576ff813884182b6c9531959b7056fbd2fda75c9a9f70d05c488?color=5a5a5a)
Die Größe des Winkels, den die beiden Randlinien im Punkt mit den Koordinaten 
einschließen beträgt damit ca. 
k)
Durch die auf den Koordinatenachsen liegenden Eckpunkten folgt für die Seitenlänge der quadratischen Grundläche:
![\( = \sqrt{8}\;[\text{LE}]\)](https://mathjax.schullv.de/ec4ebbae95cbe0202d3d6188354f00681386892670d1bc40b2a7c34273b9f643?color=5a5a5a)
Da eine Längeneinheit 15 Zentimetern entspricht, folgt für das Volumen des Quaders:
![\( = 90000\;[\text{cm}^3]\)](https://mathjax.schullv.de/14f6181870b500538b0417b079c84deed824d1f7946d0fd69b2bcad2b4f34a78?color=5a5a5a)
Da ![\(1000\;[\text{cm}^3]=1\;\ell\)](https://mathjax.schullv.de/784bdf7c6ac203191a23ec50c09f0778962337abc40f98abbc89bb6405ab3cec?color=5a5a5a)
gilt, folgt, dass der Quader ein Mindestvolumen von 
haben muss.
l)
Stammfunktion von ermitteln
Ausmultiplizieren der Funktionsgleichung von liefert 
Mit der Gleichung aus der Aufgabenstellung folgt:
Eine mögliche Stammfunktion von ist somit 
Flächeninhalt der Tischplatte berechnen
Somit hat die Tischplatte einen Flächeninhalt von ca. 
![\( = 1260\;[\text{cm}^2].\)](https://mathjax.schullv.de/4516051c304333fe62333053c2cc8d4834497ef1c6db2b410b0461f2f40d889d?color=5a5a5a)
m)
Vom Flächeninhalt der quadratischen Grundfläche aus Aufgabenteil k) kann der Flächeninhalt der ursprünglichen Tischplatte aus Aufgabenteil l) subtrahiert werden. Verdoppeln dieses berechneten Flächeninhaltes liefert den gesuchten Größenunterschied.
