Wahlaufgaben
Wahlaufgabe 1
a)
In einer Tüte befinden sich 3 rote, 5 grüne und 4 weiße Gummibärchen.
Es werden zwei Gummibärchen nacheinander, blind und ohne Zurücklegen gezogen.
Es werden zwei Gummibärchen nacheinander, blind und ohne Zurücklegen gezogen.
- Zeichne ein vollständiges Baumdiagramm.
- Berechne die Wahrscheinlichkeit, zwei weiße Gummibärchen zu ziehen.
- Berechne die Wahrscheinlichkeit, mindestens ein rotes Gummibärchen zu ziehen.
(2 Pkt.)
b)
Im Jahr 2016 wurden bei einer Zählung in Afrika noch  Elefanten gezählt. In den Jahren zuvor hatte die Zahl der Elefanten um durchschnittlich
Elefanten gezählt. In den Jahren zuvor hatte die Zahl der Elefanten um durchschnittlich  pro Jahr abgenommen.
pro Jahr abgenommen.
 Elefanten, in Simbabwe
Elefanten, in Simbabwe  Elefanten und in Kenia
Elefanten und in Kenia  Elefanten. Der Rest lebte verstreut über 15 weitere afrikanische Staaten.
Elefanten. Der Rest lebte verstreut über 15 weitere afrikanische Staaten.
- Berechne die Anzahl der voraussichtlich noch lebenden Elefanten in Afrika im Jahr 2025 bei gleichbleibendem jährlichem prozentualem Rückgang von
- Erstelle zu dieser Aussage ein Kreisdiagramm.
(2 Pkt.)
c)
Auf diesem Bild gleicht der Höcker eines Dromedars annähernd einer mathematischen Parabel.
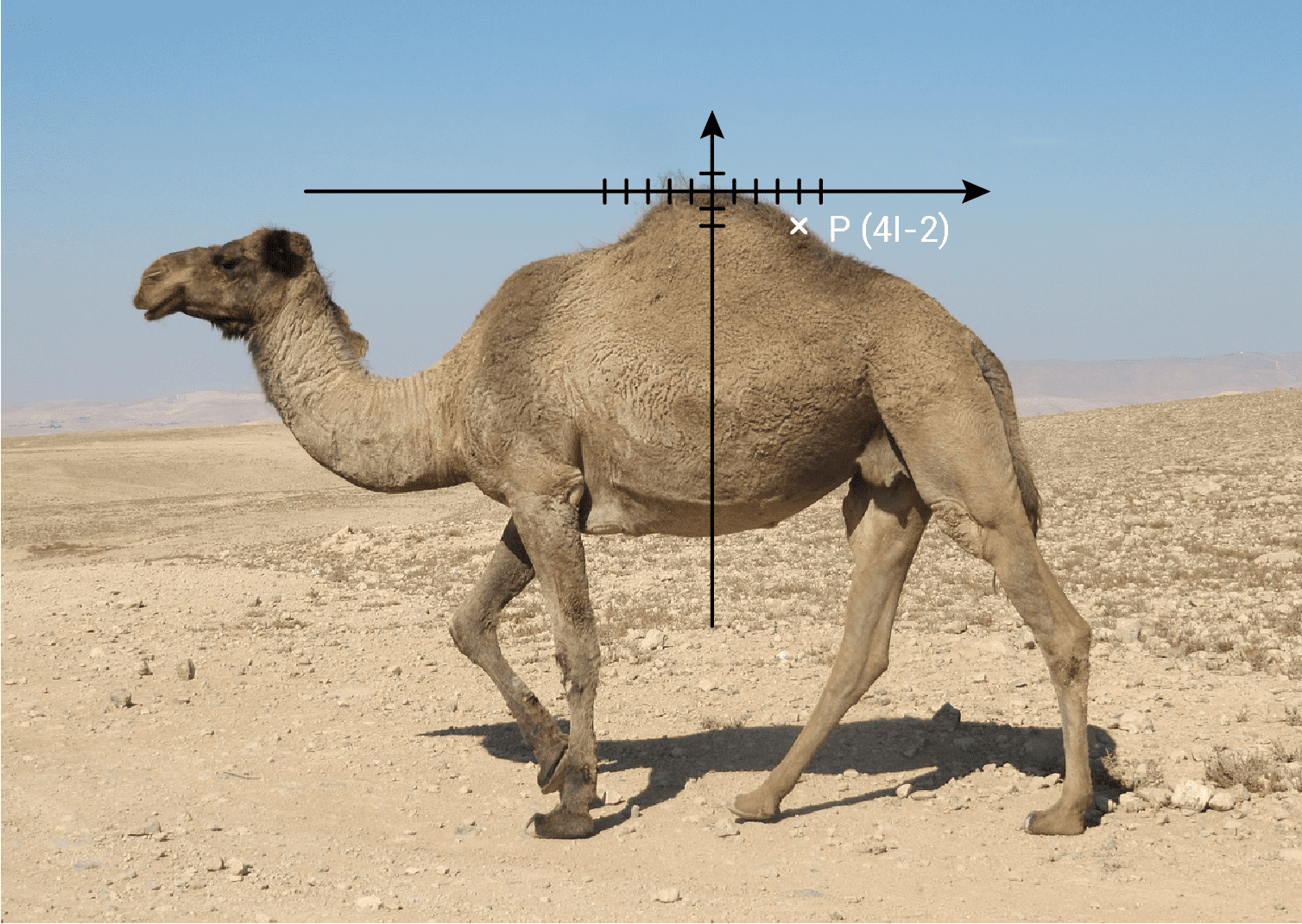
 wird um
wird um  Einheiten nach rechts und
Einheiten nach rechts und  Einheiten nach unten verschoben.
Einheiten nach unten verschoben.
Zudem wird sie um den Faktor gestreckt (Parabel wird steiler bzw. enger).
gestreckt (Parabel wird steiler bzw. enger).

- Bestimme die Gleichung der Parabel mit Hilfe des Punktes
Zudem wird sie um den Faktor
- Bestimme die Gleichung dieser Parabel.
(2 Pkt.)
Wahlaufgabe 2
a)
Verkaufszahlen eines Smartphoneherstellers
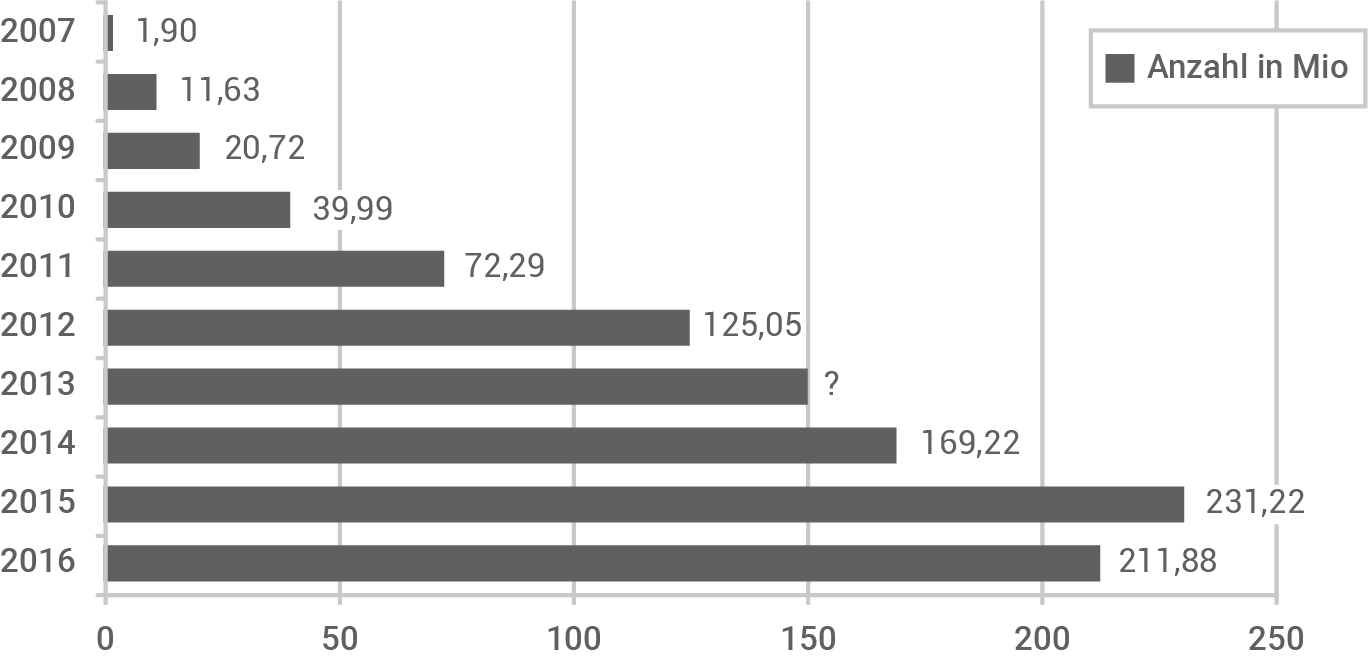 Im Jahr 2013 steigerten sich die Verkaufszahlen zum Vorjahr um
Im Jahr 2013 steigerten sich die Verkaufszahlen zum Vorjahr um 

- Berechne die Verkaufszahl für das Jahr 2013.
- Entnimm dem Schaubild die größte absolute Steigerung zwischen zwei Folgejahren.
- Zwischen welchen beiden Folgejahren war die prozentuale Steigerung am größten?
- Gib das prozentuale negative Wachstum im Vergleich zum Vorjahr an.
(2 Pkt.)
b)
Ein Flugzeug fliegt in einer konstanten Flughöhe von  über dem Meer.
über dem Meer.
Die Erdkrümmung wird vernachlässigt.
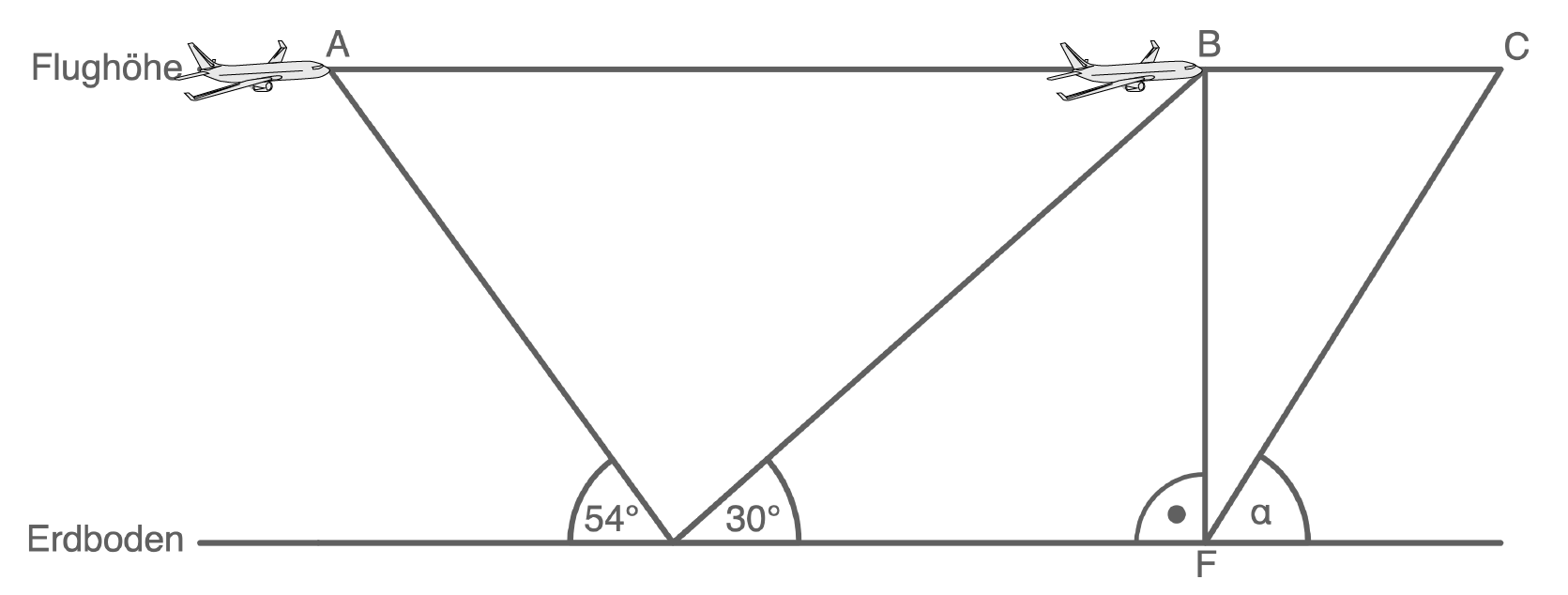
 von
von  nach
nach  Nach einer Minute hat das Flugzeug Punkt
Nach einer Minute hat das Flugzeug Punkt  erreicht.
erreicht.
Die Erdkrümmung wird vernachlässigt.

(Skizze nicht maßstabsgetreu)
- Berechne die Flugstrecke zwischen den Punkten
und
- Berechne die Strecke
- Berechne den Winkel
(2 Pkt.)
c)
Ein quadratischer Schulhof wurde vergrößert. Dazu wurde der Schulhof um  verlängert und um
verlängert und um  verbreitert. Der Schulhof hat nun eine Fläche von
verbreitert. Der Schulhof hat nun eine Fläche von 
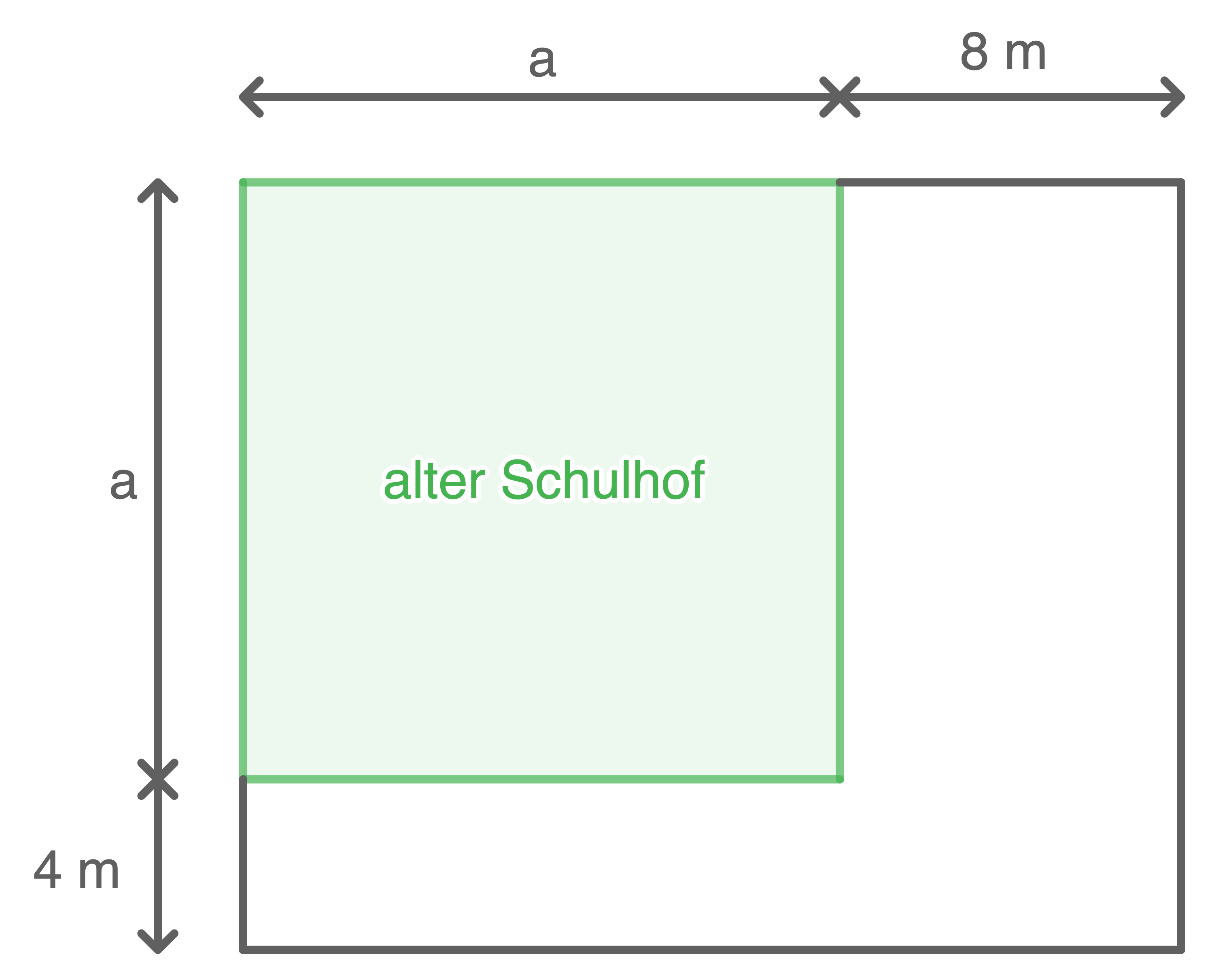

(Skizze nicht maßstabsgetreu)
- Stelle die Gleichung zur Flächenberechnung des gesamten, vergrößerten Schulhofs auf.
- Berechne die Länge und Breite des neuen Schulhofs.
(2 Pkt.)
Wahlaufgabe 3
a)
Das abgebildete Zahlenschloss (5 Einstellräder mit den Ziffern 0 bis 9) kann man nur mit einer 5-stelligen Ziffernfolge öffnen.


- Wie viele Möglichkeiten gibt es?
- Wie viele Möglichkeiten gibt es, bei denen eine Ziffer genau einmal vorkommt?
(2 Pkt.)
b)
Ein Tablet kostet  Der Händler bietet folgende Finanzierung an:
Anzahlung:
Der Händler bietet folgende Finanzierung an:
Anzahlung: 
Monatsrate:
Zinssatz: p.a.
p.a.
Monatsrate:
Zinssatz:
- Vervollständige diese Tabelle für die Finanzierung bis zur endgültigen Bezahlung.
- Wie viel Euro müssen für das Tablet insgesamt bezahlt werden?
(2 Pkt.)
c)
Das Kunstwerk (Hohlzylinder) hat einen Durchmesser von  Die Tiefe und Breite betragen jeweils
Die Tiefe und Breite betragen jeweils 


(Skizze nicht maßstabsgetreu)
- Bestimme das Volumen des Kunstwerks.
- Bestimme das Volumen und die Oberfläche (ohne die kreisförmige Grundfläche) der Halbkugel.
(2 Pkt.)
Wahlaufgabe 4
a)
Am 31.12.2005 hatte die Aktie A einen Wert von  In den folgenden 7 Jahren sank ihr Wert um jährlich durchschnittlich
In den folgenden 7 Jahren sank ihr Wert um jährlich durchschnittlich 
Danach stieg der Wert der Aktie bis zum 31.12.2018 pro Jahr im Durchschnitt um
 .
.
Am 31.12.2018 wurde diese Aktie für verkauft.
verkauft.
Danach stieg der Wert der Aktie bis zum 31.12.2018 pro Jahr im Durchschnitt um
- Berechne den Wert der Aktie am 31.12.2018.
Am 31.12.2018 wurde diese Aktie für
- Berechne das durchschnittliche jährliche Wachstum der Aktie.
(2 Pkt.)
b)
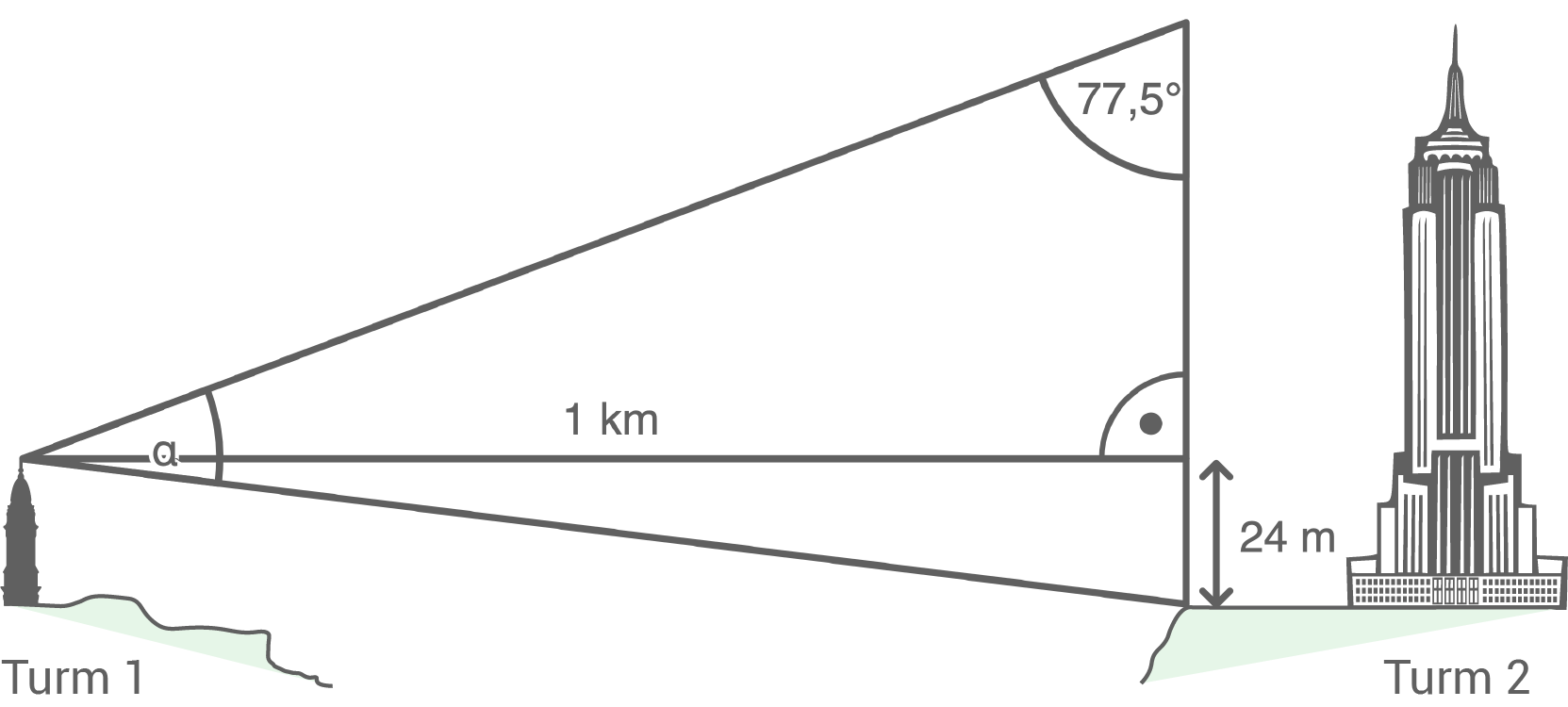
(Abbildung nicht maßstabsgetreu)
- Berechne die Höhe von Turm 2.
- Berechne den Winkel
(2 Pkt.)
c)
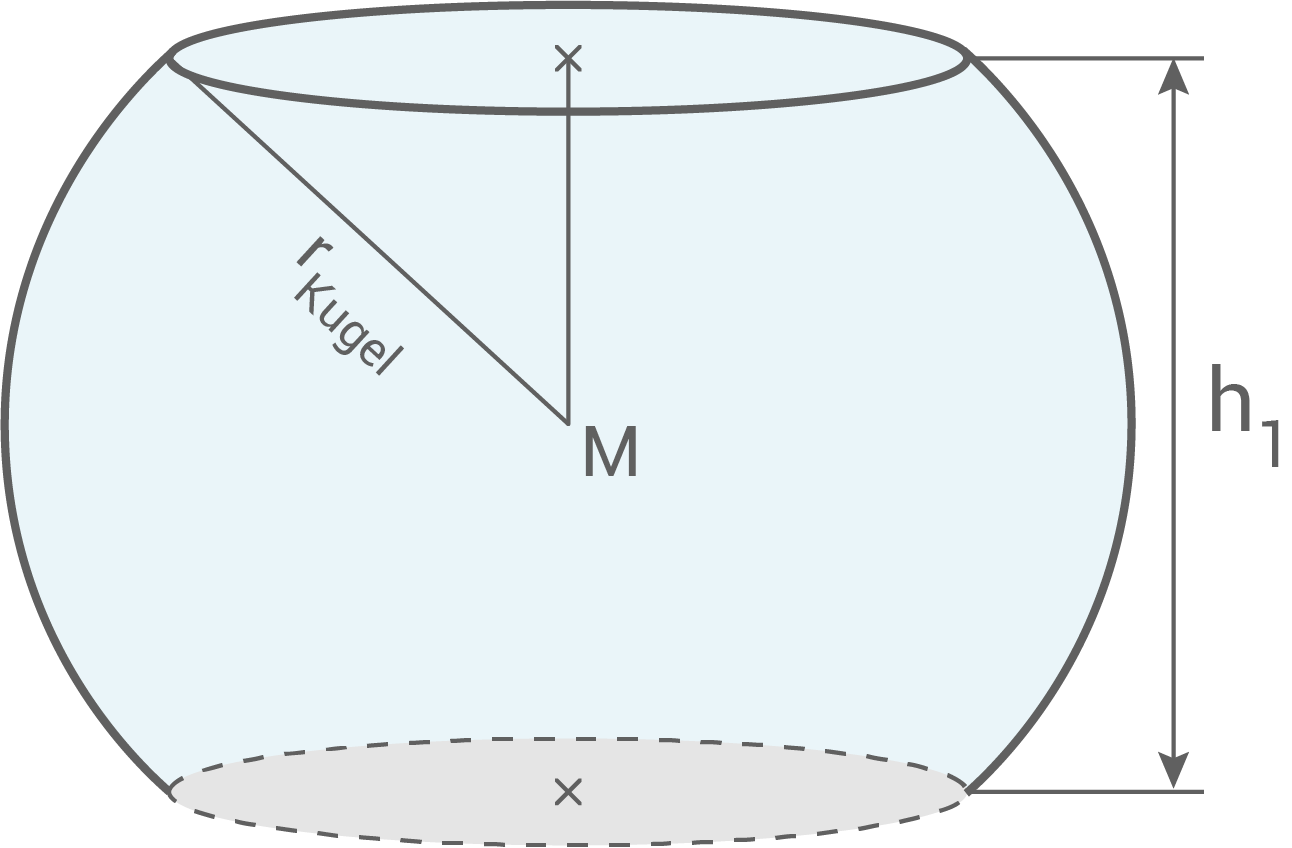
Von einer Kugel mit einem Volumen von  wurde oben und unten ein Stück weggeschnitten. Die dadurch entstandenen Kreisflächen haben je einen Flächeninhalt von
wurde oben und unten ein Stück weggeschnitten. Die dadurch entstandenen Kreisflächen haben je einen Flächeninhalt von 
Aus einem anderen Körper wird ein Kegel herausgefräst (Abb. 2).
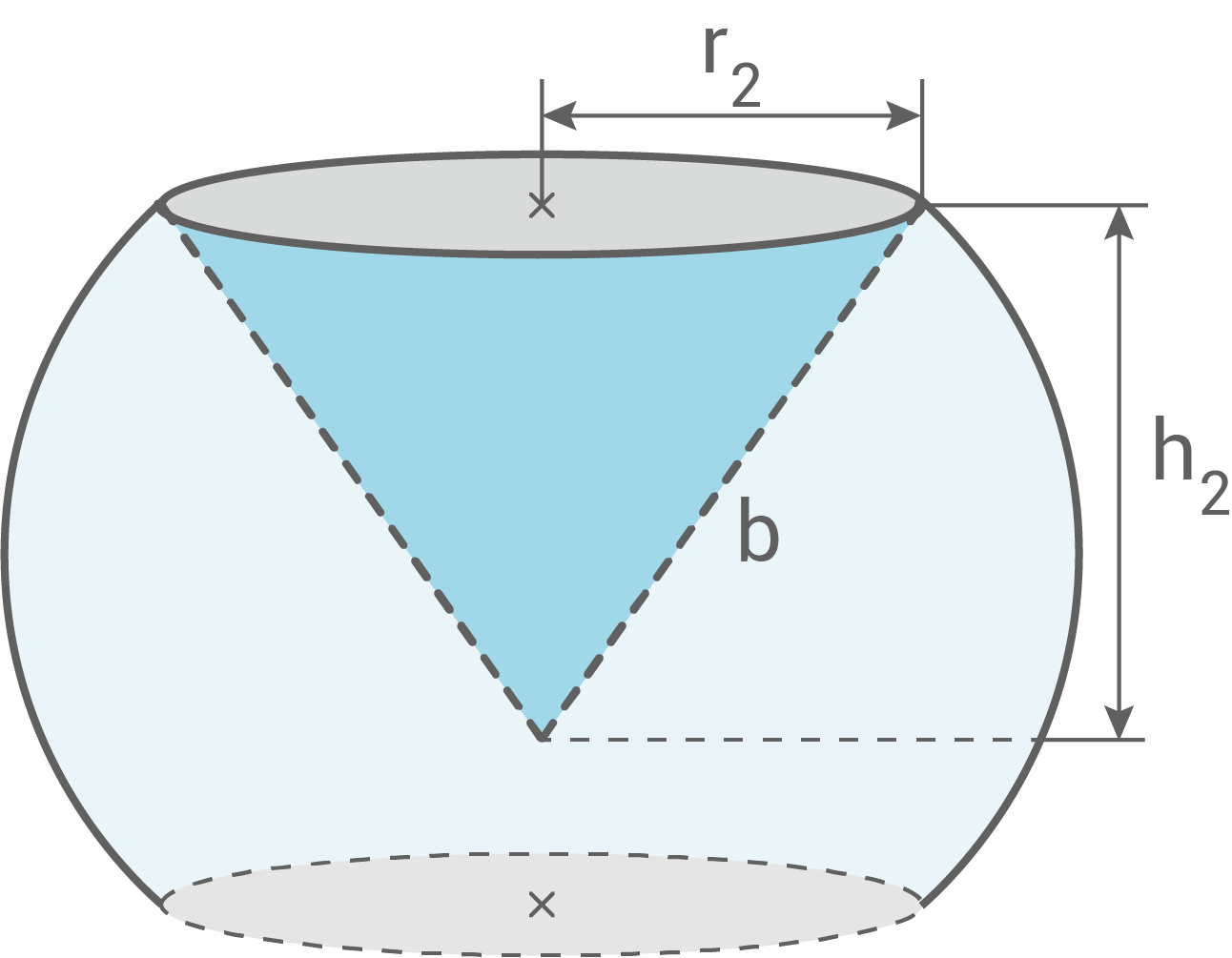


- Berechne den Radius der ursprünglichen Kugel und die Höhe
des entstandenen Körpers (Abb. 1).

Abb. 1
(Skizze nicht maßstabsgetreu)
(Skizze nicht maßstabsgetreu)

Abb. 2
(Skizze nicht maßstabsgetreu)
(Skizze nicht maßstabsgetreu)
- Berechne die Höhe
.
(2 Pkt.)
Lösung 1
a)
Baumdiagramm zeichnen
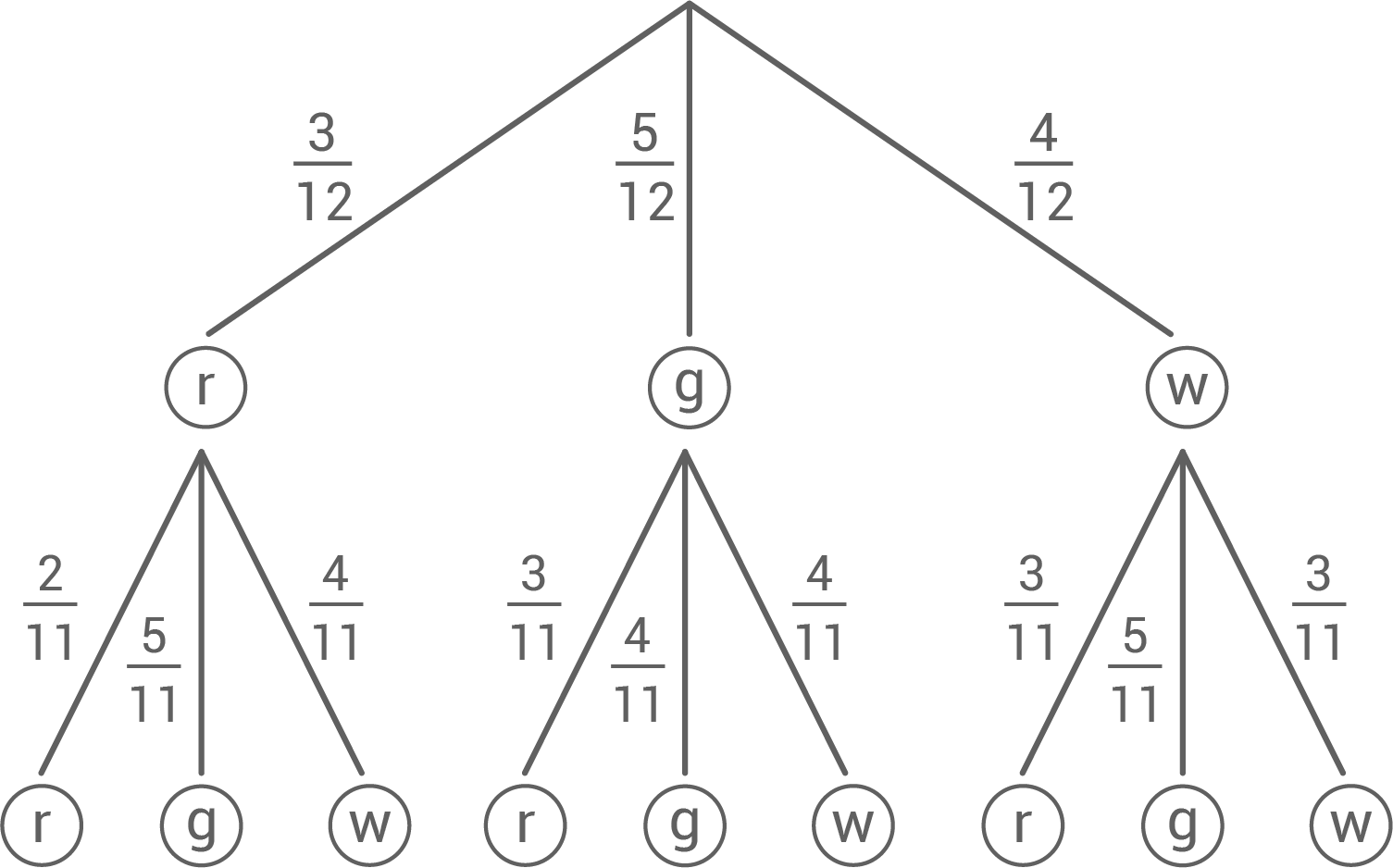 Wahrscheinlichkeit berechnen, zwei weiße Gummibärchen zu ziehen
Wahrscheinlichkeit berechnen, zwei weiße Gummibärchen zu ziehen
![\(\begin{array}[t]{rll}
P(\text{2x weiß})&=&\dfrac{4}{12}\cdot\dfrac{3}{11} \\[5pt]
&=&\boldsymbol{\dfrac{1}{11}} \\[5pt]
&\approx&0,0909 \\[5pt]
&=&\boldsymbol{9,09\,\%} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/6679c2d3fe1fa6b85eb9a407ede781289a06dc8daa47d317f78591418ed2ba1b?color=5a5a5a) Wahrscheinlichkeit berechnen, mindestens ein rotes Gummibärchen zu ziehen
Wahrscheinlichkeit berechnen, mindestens ein rotes Gummibärchen zu ziehen

b)
Anzahl der Elefanten im Jahr 2025 berechnen
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=& W_0\cdot \left(1-\dfrac{p}{100}\right)^n \\[5pt]
W_9&=& 352\,271\cdot \left(1-\dfrac{8}{100}\right)^9\\[5pt]
W_9&\approx& \boldsymbol{166\,329}
\end{array}\)](https://mathjax.schullv.de/5a1e0f6943f8626d01d003ed2dbe1c1c41c5d91e41c3218e4b91a5e64f74ab26?color=5a5a5a) Im Jahr 2025 werden voraussichtlich noch
Im Jahr 2025 werden voraussichtlich noch  Elefanten in Afrika leben.
Kreisdiagramm erstellen
Um das Kreisdiagramm zu erstellen, werden zuerst die Mittelpunktswinkel der Segmente berechnet:
Mittelpunktswinkel für das Segment „Botswana“
Elefanten in Afrika leben.
Kreisdiagramm erstellen
Um das Kreisdiagramm zu erstellen, werden zuerst die Mittelpunktswinkel der Segmente berechnet:
Mittelpunktswinkel für das Segment „Botswana“
 Mittelpunktswinkel für das Segment „Simbabwe“
Mittelpunktswinkel für das Segment „Simbabwe“
 Mittelpunktswinkel für das Segment „Kenia“
Mittelpunktswinkel für das Segment „Kenia“
 Mittelpunktswinkel für das Segment „15 weitere afrikanische Staaten“
Mittelpunktswinkel für das Segment „15 weitere afrikanische Staaten“
 Damit lässt sich nun das Kreisdiagramm zeichnen:
Damit lässt sich nun das Kreisdiagramm zeichnen:


c)
Gleichung der Parabel bestimmen
Die allgemeine Funktionsgleichung einer Parabel lautet  mit dem Scheitelpunkt
mit dem Scheitelpunkt  Bei dieser Parabel liegt der Scheitelpunkt bei
Bei dieser Parabel liegt der Scheitelpunkt bei  Der Scheitelpunkt in die allgemeine Funktionsgleichung eingesetzt, ergibt:
Der Scheitelpunkt in die allgemeine Funktionsgleichung eingesetzt, ergibt:
![\(\begin{array}[t]{rll}
y&=& a(x-d)^2+e \\[5pt]
y&=& a(x-0)^2+0 \\[5pt]
y&=& ax^2
\end{array}\)](https://mathjax.schullv.de/24edc24fd65f3b5c5750c2df146f96e2243868322524ac1a02abb64fe6f54d41?color=5a5a5a) Die gesuchte Parabelgleichung hat also die Form
Die gesuchte Parabelgleichung hat also die Form  Der Punkt
Der Punkt  in die Parabelgleichung eingesetzt, ergibt:
in die Parabelgleichung eingesetzt, ergibt:
![\(\begin{array}[t]{rll}
y&=& ax^2\\[5pt]
-2&=& a\cdot 4^2\\[5pt]
-2&=& a\cdot 16&\quad \scriptsize \mid\;:16 \\[5pt]
\dfrac{-2}{16}&=& a& \\[5pt]
a&=&-\dfrac{1}{8}
\end{array}\)](https://mathjax.schullv.de/185813231917334515161760f66cf41927f6a02b55b894b978def22034d72e14?color=5a5a5a) Somit hat die Parabel die Gleichung
Somit hat die Parabel die Gleichung  Gleichung einer neuen Parabel bestimmen
Die allgemeine Funktionsgleichung einer Parabel lautet
Gleichung einer neuen Parabel bestimmen
Die allgemeine Funktionsgleichung einer Parabel lautet  mit dem Scheitelpunkt
mit dem Scheitelpunkt  Scheitelpunkt
Scheitelpunkt  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
y&=& a(x-d)^2+e \\[5pt]
y&=& a(x-1)^2+0 \\[5pt]
y&=& a(x-1)^2
\end{array}\)](https://mathjax.schullv.de/7ebf8acc73f7a6e7ac38b9fd9603b8a1d58377b721699b3222dea9f4ac4cce0c?color=5a5a5a) Parabel um
Parabel um  Einheiten nach rechts verschieben
Einheiten nach rechts verschieben
![\(\begin{array}[t]{rll}
y&=& a(x-1)^2\\[5pt]
y&=& a(x-1-4)^2\\[5pt]
y&=& a(x-5)^2
\end{array}\)](https://mathjax.schullv.de/886c0c84b3d61b7adf7b36f262bbc231fc7aa4f726c29afc55d3ec9cc67581f8?color=5a5a5a) Parabel um
Parabel um  Einheiten nach unten verschieben
Einheiten nach unten verschieben
![\(\begin{array}[t]{rll}
y&=& a(x-5)^2\\[5pt]
y&=& a(x-5)^2-3
\end{array}\)](https://mathjax.schullv.de/8302c901e0db34f6a09488a8b67ec890d16224344949543778f0dd0894b3dfac?color=5a5a5a) Parabel strecken
Parabel strecken

Lösung 2
a)
Verkaufszahl für das Jahr 2013 berechnen
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot \left(1+\dfrac{p}{100}\right)^n\\[5pt]
W_1&=&125,05\,\text{Mio.}\cdot \left(1+\dfrac{20,6}{100}\right)^1\\[5pt]
W_1&\approx&\boldsymbol{150,81\,\text{Mio.}}
\end{array}\)](https://mathjax.schullv.de/e280e6c2ffcf7c79eea03453392917cd0fd09519a3a6b23e7c84d3a5436d6987?color=5a5a5a) Zwischen welchen beiden Folgejahren war die absolute Steigerung am größten?
Die größte absolute Steigerung war zwischen 2015 und 2014.
Zwischen welchen beiden Folgejahren war die prozentuale Steigerung am größten?
Formel zur Berechnung der prozentualen Steigerung:
Zwischen welchen beiden Folgejahren war die absolute Steigerung am größten?
Die größte absolute Steigerung war zwischen 2015 und 2014.
Zwischen welchen beiden Folgejahren war die prozentuale Steigerung am größten?
Formel zur Berechnung der prozentualen Steigerung:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot q^n & \\[5pt]
W_n&=&W_0\cdot q^1 &\\[5pt]
W_n&=&W_0\cdot q&\quad \scriptsize \mid\; :W_0\\[5pt]
\dfrac{W_n}{W_0}&=& q&\\[5pt]
q&=&\dfrac{W_n}{W_0}&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/7fc2fccffd6f1c1a570ed11bbf42beb655b96443170ebfbfeba2d6624bd3b714?color=5a5a5a)

![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot q^n&\\[5pt]
W_1&=&W_0\cdot q^1&\quad \scriptsize \mid\; :W_0\\[5pt]
\dfrac{W_1}{W_0}&=&q&\\[5pt]
q&=&\dfrac{211,88\,\text{Mio.}}{231,22\,\text{Mio.}}&\\[5pt]
q&\approx&0,92&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/1316e3953f4a8c830e5ecdd20f3400cd89b146890b5b0036901d80cb6e07b093?color=5a5a5a)

 Das negative Wachstum beträgt
Das negative Wachstum beträgt 
Prozentuale Steigerung 2007 - 2008
![\(\begin{array}[t]{rll}
q&=&\dfrac{W_n}{W_0}&\\[5pt]
q&=&\dfrac{11,63}{1,90}\\[5pt]
q&\approx&6,12
\end{array}\)](https://mathjax.schullv.de/019b3c260c8216547f7eef91ccb9841b77b9ddab63f205a99fd1ceb14834bd02?color=5a5a5a)

Prozentuale Steigerung 2008 - 2009
![\(\begin{array}[t]{rll}
q&=&\dfrac{W_n}{W_0}&\\[5pt]
q&=&\dfrac{20,72}{11,63}\\[5pt]
q&\approx&1,78
\end{array}\)](https://mathjax.schullv.de/b5435cb76333aace55560e078013b43b6a46e556390b8b406a4232c827e704eb?color=5a5a5a)

Prozentuale Steigerung 2009 - 2010
![\(\begin{array}[t]{rll}
q&=&\dfrac{W_n}{W_0}&\\[5pt]
q&=&\dfrac{39,99}{20,72}\\[5pt]
q&\approx&1,93
\end{array}\)](https://mathjax.schullv.de/60cb6fabd06597ec1cf71976b9494bdb16c3606fef6dc3c0aac9fd194493cb19?color=5a5a5a)

Prozentuale Steigerung 2010 - 2011
![\(\begin{array}[t]{rll}
q&=&\dfrac{W_n}{W_0}&\\[5pt]
q&=&\dfrac{72,29}{39,99}\\[5pt]
q&\approx&1,81
\end{array}\)](https://mathjax.schullv.de/a1918143ad54270c8d9b316c2113044bb84102ff40934a26dd3850ed38b44370?color=5a5a5a)

Prozentuale Steigerung 2011 - 2012
![\(\begin{array}[t]{rll}
q&=&\dfrac{W_n}{W_0}&\\[5pt]
q&=&\dfrac{125,05}{72,29}\\[5pt]
q&\approx&1,73
\end{array}\)](https://mathjax.schullv.de/759c672d34d5c06dd7202e5586e81b09a724929f6ea4c90218fc67369b72e481?color=5a5a5a)

Prozentuale Steigerung 2012 - 2013
![\(\begin{array}[t]{rll}
q&=&\dfrac{W_n}{W_0}&\\[5pt]
q&=&\dfrac{150,81}{125,05}\\[5pt]
q&\approx&1,21
\end{array}\)](https://mathjax.schullv.de/e409313e9df8f0ed17d1582218790c0f3f8a60d3bacfb6ba1ba435028f6bf39e?color=5a5a5a)

Prozentuale Steigerung 2013 - 2014
![\(\begin{array}[t]{rll}
q&=&\dfrac{W_n}{W_0}&\\[5pt]
q&=&\dfrac{169,22}{150,81}\\[5pt]
q&\approx&1,12
\end{array}\)](https://mathjax.schullv.de/fc8626a3f13bdd6dc2fcd27c02a0a9fb26397a8efa11aa8ad9bcf5e661beacbf?color=5a5a5a)

Prozentuale Steigerung 2014 - 2015
![\(\begin{array}[t]{rll}
q&=&\dfrac{W_n}{W_0}&\\[5pt]
q&=&\dfrac{231,22}{169,22}\\[5pt]
q&\approx&1,37
\end{array}\)](https://mathjax.schullv.de/a52b9de6b146c78420e57d371cdec4dc34369db00274cbd8a94913c1089a97ff?color=5a5a5a)

Die größte prozentuale Steigerung war zwischen 2007 und 2008.
Das prozentuale negative Wachstum angeben
Gegeben:
b)
Flugstrecke zwischen den Punkten  und
und  berechnen
berechnen
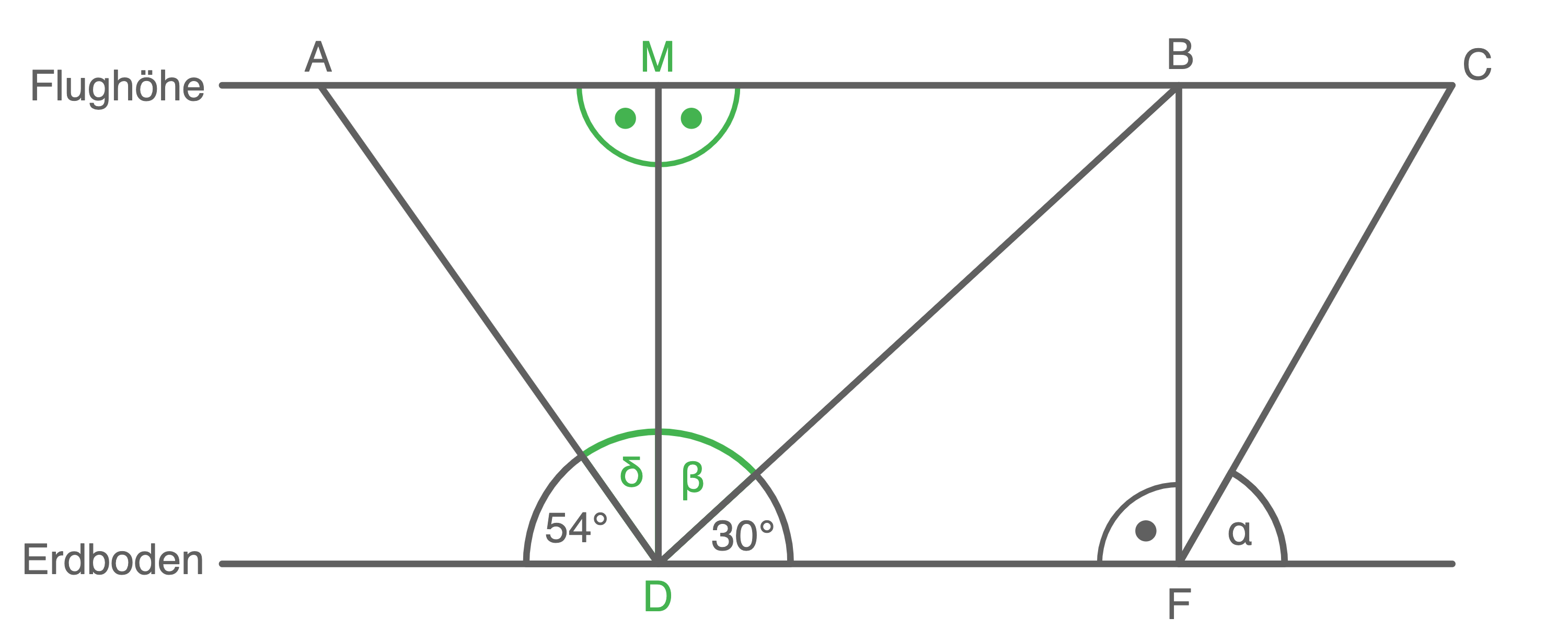 Größe des Winkels
Größe des Winkels  berechnen
berechnen
 Größe des Winkels
Größe des Winkels  berechnen
berechnen
 Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\delta)&=&\dfrac{\overline{AM}}{\overline{MD}} &\quad \scriptsize \mid\; \cdot \overline{MD}\\[5pt]
\tan(\delta)\cdot \overline{MD}&=&\overline{AM}\\[5pt]
\overline{AM}&=&\tan(\delta)\cdot \overline{MD}\\[5pt]
\overline{AM}&=&\tan(36^{\circ})\cdot 10\,000\,\text{m}\\[5pt]
\overline{AM}&\approx&7\,265,43\,\text{m}
\end{array}\)](https://mathjax.schullv.de/244c54d0ef67fc8d72c588476ffa1ccba8024a66b0d37f2f6b4ce0d9634e4826?color=5a5a5a) Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{MB}}{\overline{MD}} &\quad \scriptsize \mid\; \cdot \overline{MD}\\[5pt]
\tan(\beta)\cdot \overline{MD}&=&\overline{MB} \\[5pt]
\overline{MB}&=&\tan(\beta)\cdot \overline{MD} \\[5pt]
\overline{MB}&=&\tan(60^{\circ})\cdot 10\,000\,\text{m} \\[5pt]
\overline{MB}&\approx&17\,320,51\,\text{m}
\end{array}\)](https://mathjax.schullv.de/f079bb773b90fde38dc6c4691b90f3e104f1e2aa760cfe5fd6ec041fd5ce190b?color=5a5a5a) Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AB}&=&\overline{AM}+\overline{MB} \\[5pt]
\overline{AB}&=&7\,265,43\,\text{m}+17\,320,51\,\text{m} \\[5pt]
\overline{AB}&=&\boldsymbol{24\,585,94\,\text{m}}
\end{array}\)](https://mathjax.schullv.de/51d654959e6893df49df2a4c75d4571f1b8ffa9b9f4a1a5d5c42570d12fe26da?color=5a5a5a) Die Flugstrecke zwischen
Die Flugstrecke zwischen  und
und  beträgt
beträgt  Länge von
Länge von  berechnen
Dafür wird die Formel zur Berechnung der Geschwindigkeit nach
berechnen
Dafür wird die Formel zur Berechnung der Geschwindigkeit nach  umgestellt:
umgestellt:
![\(\begin{array}[t]{rll}
v&=&\dfrac{s}{t} &\quad \scriptsize \mid\;\cdot t \\[5pt]
v\cdot t&=&s & \\[5pt]
s&=&v\cdot t & \\[5pt]
s&=&960\dfrac{\text{km}}{\text{h}}\cdot 1\,\text{min} & \\[5pt]
s&=&960\dfrac{\text{km}}{\text{h}}\cdot \dfrac{1}{60}\,\text{h} & \\[5pt]
s&=&\boldsymbol{16\,\text{km}} & \\[5pt]
s&=&\boldsymbol{16\,000\,\text{m}} & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/c78b90ea0546b3442e4a9863f228dfb6da4cf55e699c1064844ac6fd3f2efe48?color=5a5a5a) Die Länge von
Die Länge von  beträgt
beträgt  Größe des Winkels
Größe des Winkels  berechnen
berechnen
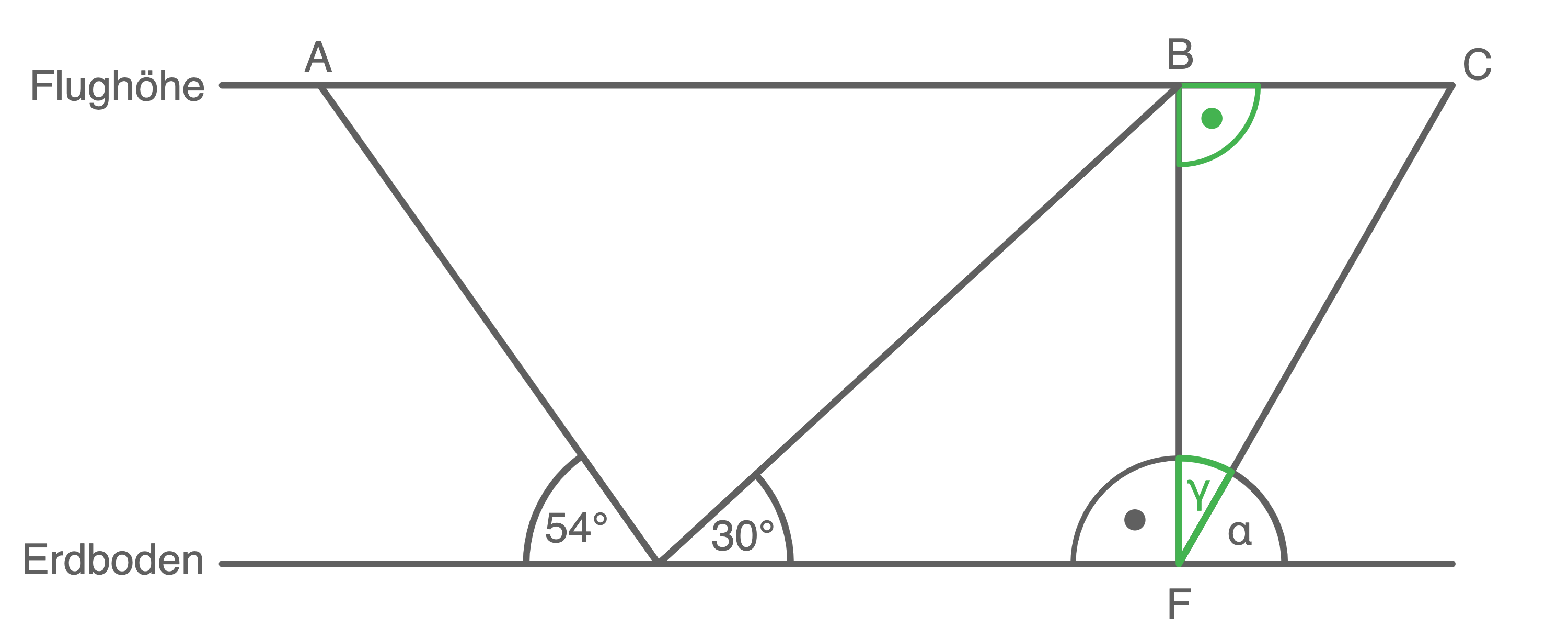
![\(\begin{array}[t]{rll}
\tan(\gamma)&=&\dfrac{\overline{BC}}{\overline{BF}} & \\[5pt]
\tan(\gamma)&=&\dfrac{16\,000\,\text{m}}{10\,000\,\text{m}} &\quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\tan(\gamma)&\approx&58^{\circ}
\end{array}\)](https://mathjax.schullv.de/0548f1e03ce70b086c2a5363fea644c9e573435060d212c1fbb565e7c6a50d09?color=5a5a5a) Daraus folgt:
Daraus folgt: 


c)
Gleichung zur Flächenberechnung aufstellen
 Länge und Breite des neuen Schulhofs berechnen
Länge und Breite des neuen Schulhofs berechnen
![\(\begin{array}[t]{rll}
A&=&(a\cdot 4\,\text{m})\cdot(a\cdot 8\,\text{m}) &\\[5pt]
725\,\text{m}^2&=&(a\cdot 4\,\text{m})\cdot(a\cdot 8\,\text{m})\\[5pt]
725\,\text{m}^2&=&a^2+8\,\text{m}\cdot a+4\,\text{m}\cdot a+32\,\text{m}^2 &\\[5pt]
725\,\text{m}^2&=&a^2+12\,\text{m}\cdot a+32\,\text{m}^2 \quad \scriptsize \mid\; -725\,\text{m}^2\\[5pt]
0&=&a^2+12\,\text{m}\cdot a-693\,\text{m}^2 \\[5pt]
a_{1/2}&=&-\dfrac{12\,\text{m}}{2}\pm\sqrt{\left(\dfrac{12\,\text{m}}{2}\right)^2+693\,\text{m}^2} \\[5pt]
a_{1/2}&=&-6\,\text{m}\pm\sqrt{729\,\text{m}^2} \\[5pt]
a_{1}&=&-6+27\,\text{m}=21\,\text{m} \\[5pt]
a_{2}&=&-6-27\,\text{m}=-33\,\text{m}
\end{array}\)](https://mathjax.schullv.de/ce958a5424407157cf310350a62e0f4b592eca296a731ab3b32143cb7e309229?color=5a5a5a) Da eine Längenangabe nicht negativ sein kann, gilt:
Da eine Längenangabe nicht negativ sein kann, gilt:  Daraus folgt für die Länge und Breite des neuen Schulhofs:
Daraus folgt für die Länge und Breite des neuen Schulhofs:
Lösung 3
a)
Wie viele Möglichkeiten gibt es?
Da es  Ziffern und
Ziffern und  Einstellräder gibt, gibt es
Einstellräder gibt, gibt es  Möglichkeiten.
Wie viele Möglichkeiten gibt es, bei denen eine Ziffer genau einmal vorkommt?
Es gibt
Möglichkeiten.
Wie viele Möglichkeiten gibt es, bei denen eine Ziffer genau einmal vorkommt?
Es gibt  Möglichkeiten, dass eine Ziffer genau einmal vorkommt.
Möglichkeiten, dass eine Ziffer genau einmal vorkommt.
b)
Tabelle vervollständigen
Kredithöhe
 Zinssatz pro Monat
Zinssatz pro Monat
 Beispiel zur Berechnung der Zinsen
Beispiel zur Berechnung der Zinsen
 Beispiel zur Berechnung der Tilgung
Beispiel zur Berechnung der Tilgung
 Beispiel zur Berechnung des Kredits am Monatsende
Beispiel zur Berechnung des Kredits am Monatsende
 Wie viel Euro müssen für das Tablet insgesamt bezahlt werden?
Dafür müssen der Kaufpreis und die Zinsen an die Bank addiert werden:
Wie viel Euro müssen für das Tablet insgesamt bezahlt werden?
Dafür müssen der Kaufpreis und die Zinsen an die Bank addiert werden:

 Es müssen insgesamt
Es müssen insgesamt  für das Tablet gezahlt werden.
für das Tablet gezahlt werden.
c)
Volumen des Kunstwerks bestimmen
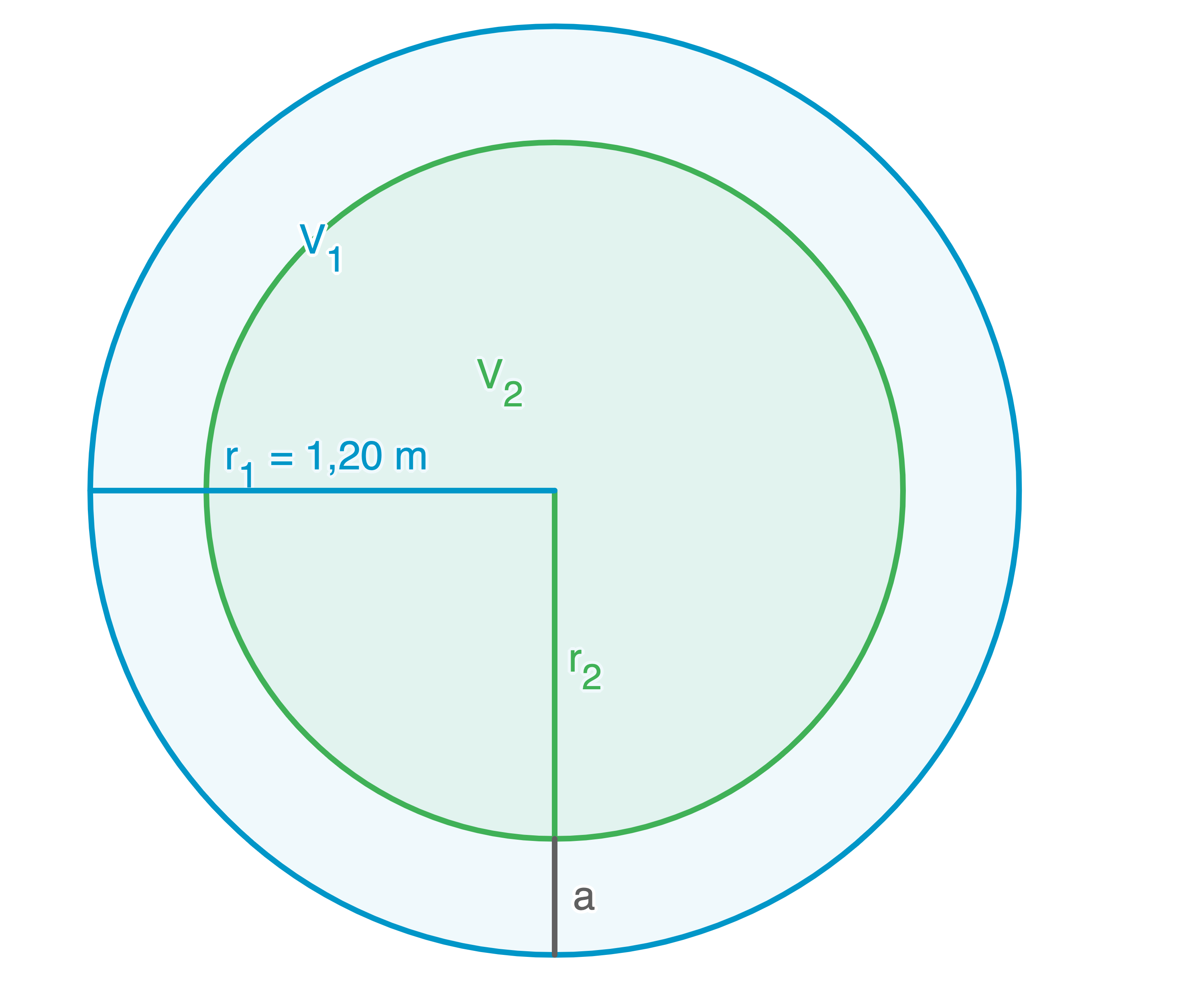 Formel zur Volumenberechnung eines Hohlzylinders:
Formel zur Volumenberechnung eines Hohlzylinders: 
 berechnen
berechnen
![\(\begin{array}[t]{rll}
V_1&=& \pi\cdot r_1^{\,\,2}\cdot h \\[5pt]
V_1&=& \pi\cdot (1,20\,\text{m})^{2}\cdot 0,20\,\text{m} \\[5pt]
V_1&\approx&0,905\,\text{m}^3
\end{array}\)](https://mathjax.schullv.de/e619749e869339b0be35e17f78f95831b65fd0e9280ee1a0db83fc8c124566f9?color=5a5a5a)
 berechnen
berechnen
![\(\begin{array}[t]{rll}
r_2&=&(d:2)-a \\[5pt]
r_2&=&(2,40:2\,\text{m})-0,20\,\text{m} \\[5pt]
r_2&=&1,00\,\text{m}
\end{array}\)](https://mathjax.schullv.de/b4f8844f459fd4c8d54a48b971b06881cd07ba0b133bafb41aa46416ff666351?color=5a5a5a)
 berechnen
berechnen
![\(\begin{array}[t]{rll}
V_2&=& \pi\cdot r_2^{\,\,2}\cdot h \\[5pt]
V_2&=& \pi\cdot (1,00\,\text{m})^{2}\cdot 0,20\,\text{m} \\[5pt]
V_2&\approx&0,628\,\text{m}^3
\end{array}\)](https://mathjax.schullv.de/dfd0902b4251326ab7d2ce4ef4571af069d61c4c451cce3fa191b38e4d224ba1?color=5a5a5a)
 berechnen
berechnen
![\(\begin{array}[t]{rll}
V_H&=& V_1-V_2 \\[5pt]
V_H&=& 0,905\,\text{m}^3-0,628\,\text{m}^3 \\[5pt]
V_H&=& \boldsymbol{0,277\,\text{m}^3}
\end{array}\)](https://mathjax.schullv.de/f4227c247f2da1392d3e52b0c66d3ec82f088fbcbb9cb23d0257d463ee0efda1?color=5a5a5a) Volumen der Halbkugel bestimmen
Volumen der Halbkugel bestimmen
![\(\begin{array}[t]{rll}
V&=&\dfrac{1}{2}\cdot \dfrac{4}{3}\cdot \pi\cdot (1,20\,\text{m})^3& \\[5pt]
V&\approx&\boldsymbol{3,62\,\text{m}^3}
\end{array}\)](https://mathjax.schullv.de/64cedd16ef2445b66bcc76a094b720ca398dd8e5d8b41be73141c5e40783518f?color=5a5a5a) Oberflächeninhalt der Halbkugel bestimmen
Oberflächeninhalt der Halbkugel bestimmen
![\(\begin{array}[t]{rll}
O&=& \dfrac{1}{2}\cdot4\cdot \pi\cdot r^2\\[5pt]
O&=& \dfrac{1}{2}\cdot4\cdot \pi\cdot (1,20\,\text{m})^2\\[5pt]
O&\approx& \boldsymbol{9,05\,\text{m}^2}
\end{array}\)](https://mathjax.schullv.de/ab8e5542bede0e545d2f1a328892492b10f53e46507cdd69f22222bd2f0c7bbe?color=5a5a5a)

Lösung 4
a)
Wert der Aktie am 31.12.2018 berechnen
Wert der Aktie nach 7 Jahren (am 31.12.2012)
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot \left(1-\dfrac{p}{100}\right)^n \\[5pt]
W_7&=&200,00\,€\cdot \left(1-\dfrac{1,1}{100}\right)^7 \\[5pt]
W_7&\approx&185,10\,€
\end{array}\)](https://mathjax.schullv.de/157917d2149ac63e4e0da97b5766b29f6c6ca82fdd6fa74cc5ff25c2bbd74e23?color=5a5a5a) Wert der Aktie nach weiteren 6 Jahren (am 31.12.2018)
Gegeben:
Wert der Aktie nach weiteren 6 Jahren (am 31.12.2018)
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot \left(1+\dfrac{p}{100}\right)^n \\[5pt]
W_6&=&185,10\,€\cdot \left(1+\dfrac{2,2}{100}\right)^6 \\[5pt]
W_6&\approx&\boldsymbol{210,92\,€}
\end{array}\)](https://mathjax.schullv.de/3e215d720a3e804ff3b38a5521461150d6a7008ca4c937beb8325147203f687c?color=5a5a5a) Der Wert der Aktie am 31.12.2018 beträgt
Der Wert der Aktie am 31.12.2018 beträgt  Das durchschnittliche jährliche Wachstum der Aktie berechnen
Gegeben:
Das durchschnittliche jährliche Wachstum der Aktie berechnen
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot q^n \\[5pt]
W_6&=&W_0\cdot q^6 &\quad \scriptsize \mid\;:W_0 \\[5pt]
\dfrac{W_6}{W_0}&=&q^6 \\[5pt]
q^6&=&\dfrac{W_6}{W_0} &\quad \scriptsize \mid\;\sqrt[6]{\,\,} \\[5pt]
q&=&\sqrt[6]{\dfrac{W_6}{W_0}} \\[5pt]
q&=&\sqrt[6]{\dfrac{64,77\,€}{53,00\,€}} \\[5pt]
q&\approx&1,034 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/e6ddcd4f9fa68454d04d6c853a17d7c534fa6ae6bf314a51c6d9cb0d5f6f4449?color=5a5a5a)

 Das durchschnittliche jährliche Wachstum der Aktie beträgt
Das durchschnittliche jährliche Wachstum der Aktie beträgt 
b)
Höhe von Turm 2 berechnen
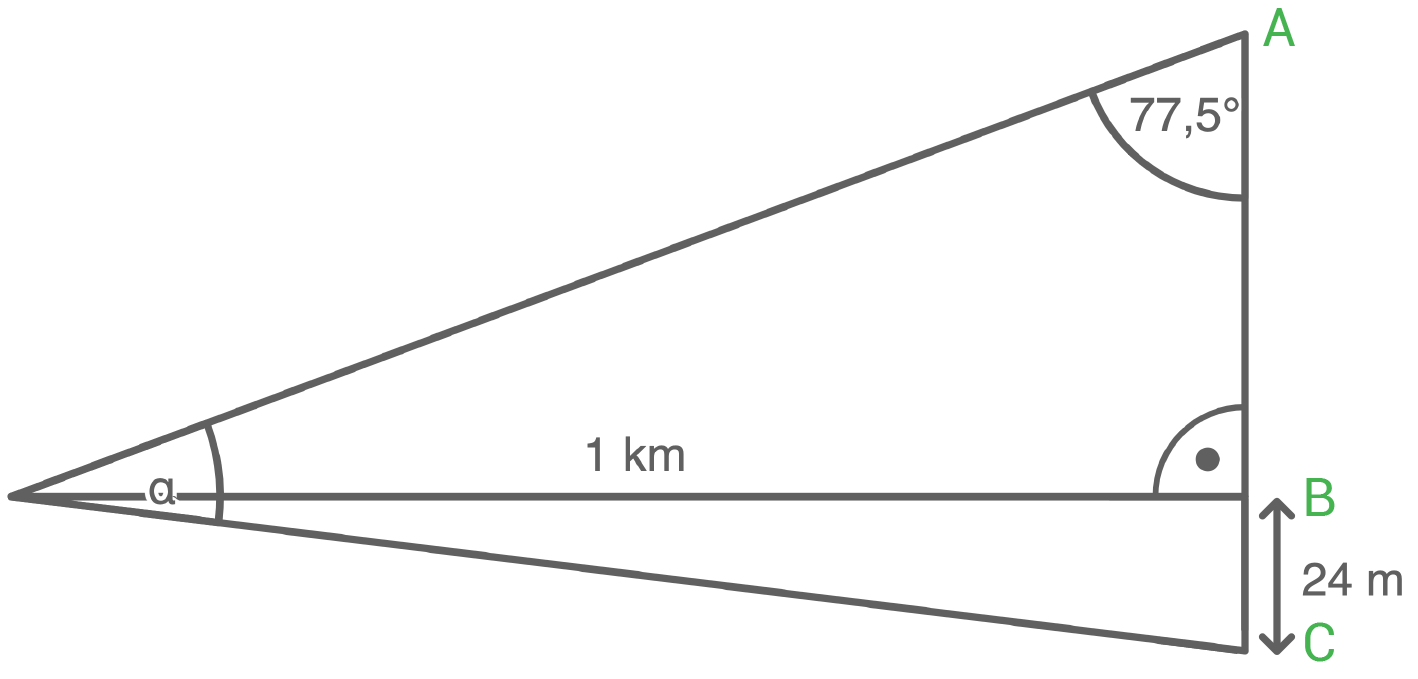 Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(77,5^{\circ})&=&\dfrac{1\,\text{km}}{\overline{AB}}\\[5pt]
\tan(77,5^{\circ})&=&\dfrac{1\,000\,\text{m}}{\overline{AB}} &\quad \scriptsize \mid\;\cdot \overline{AB} \\[5pt]
\tan(77,5^{\circ})\cdot \overline{AB} &=&1\,000\,\text{m}&\quad \scriptsize \mid\;:\tan(77,5^{\circ})\\[5pt]
\overline{AB}&=&\dfrac{1\,000\,\text{m}}{\tan(77,5^{\circ})}\\[5pt]
\overline{AB}&\approx&221,69\,\text{m}
\end{array}\)](https://mathjax.schullv.de/54f5d572a949262a480f7f1ea981c0e1ed6a8cb055e2ef28ae317515338d35e4?color=5a5a5a) Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AC}&=&\overline{AB}+\overline{BC} \\[5pt]
\overline{AC}&=&221,69\,\text{m}+24\,\text{m} \\[5pt]
\overline{AC}&=&\boldsymbol{245,69\,\text{m}}
\end{array}\)](https://mathjax.schullv.de/e9d99edea9b011332218dbd386fd65870f3c0f880ce23d19d870cf2d4cfa33c3?color=5a5a5a) Turm 2 hat eine Höhe von
Turm 2 hat eine Höhe von  Größe des Winkels
Größe des Winkels  berechnen
berechnen
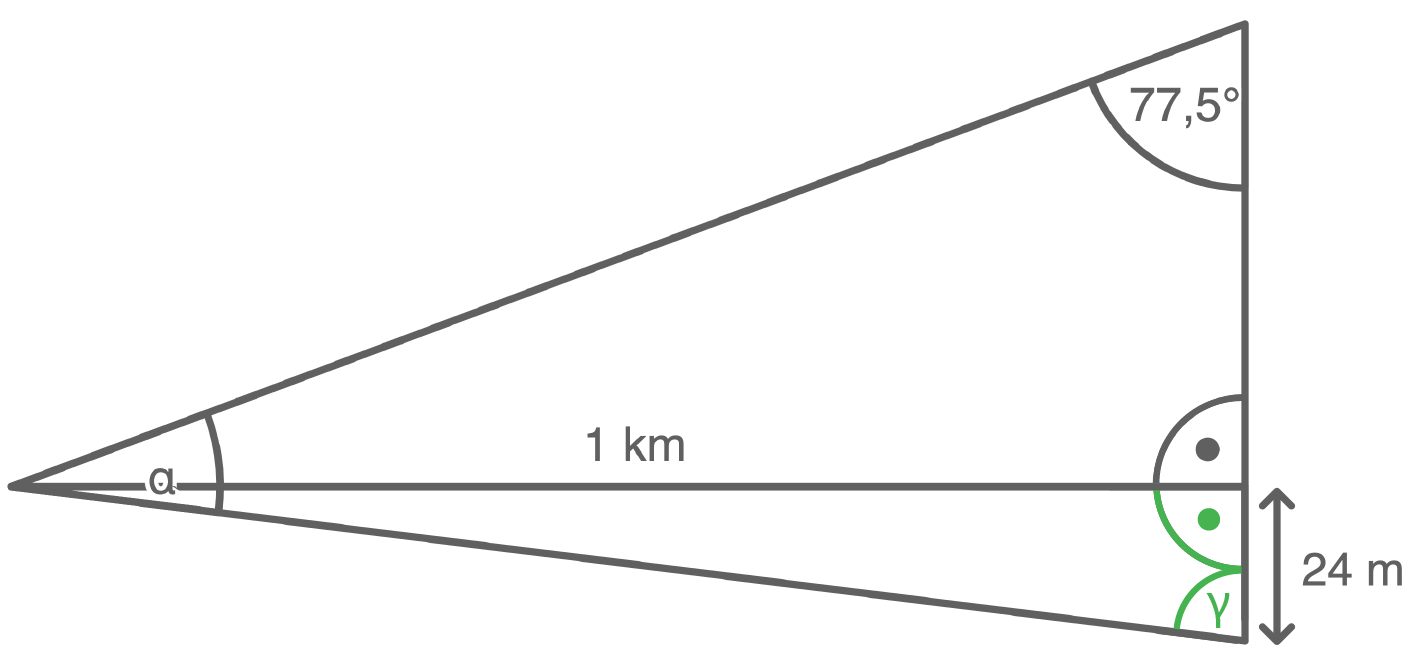 Größe des Winkels
Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\gamma)&=&\dfrac{1\,000\,\text{m}}{24\,\text{m}} &\quad \scriptsize \mid\;\tan^{-1} \\[5pt]
\gamma&\approx&88,6^{\circ}
\end{array}\)](https://mathjax.schullv.de/34247b70deaa42ccc2f09e54016c6161b2ede6bad9a569c80d6e6dca049af8e2?color=5a5a5a) Damit folgt für den Winkel
Damit folgt für den Winkel 
![\(\begin{array}[t]{rll}
\alpha&=&180^{\circ}-77,5^{\circ}-88,6^{\circ}\\[5pt]
\alpha&=&\boldsymbol{13,9^{\circ}}
\end{array}\)](https://mathjax.schullv.de/ac483bef32f221f4f3725b33417295eed2df04d98edcc9fcf10a6945fcfa4fc2?color=5a5a5a) Der Winkel
Der Winkel  hat eine Größe von
hat eine Größe von 


c)
Radius der ursprünglichen Kugel berechnen
![\(\begin{array}[t]{rll}
V&=&\dfrac{4}{3}\cdot \pi\cdot r_{\text{Kugel}}^{\,\,\,\,\,\,\,\,\,\,3} &\quad \scriptsize \mid\;\cdot \dfrac{3}{4} \\[5pt]
\dfrac{3}{4}\cdot V&=&\pi\cdot r_{\text{Kugel}}^{\,\,\,\,\,\,\,\,\,\,3} &\quad \scriptsize \mid\;: \pi\\[5pt]
\dfrac{3}{4}\cdot \dfrac{V}{\pi}&=&r_{\text{Kugel}}^{\,\,\,\,\,\,\,\,\,\,3} &\\[5pt]
r_{\text{Kugel}}^{\,\,\,\,\,\,\,\,\,\,3}&=&\dfrac{3}{4}\cdot \dfrac{V}{\pi} &\quad \scriptsize \mid\;\sqrt[3]{\,\,}\\[5pt]
r_{\text{Kugel}}&=&\sqrt[3]{\dfrac{3}{4}\cdot \dfrac{V}{\pi} }\\[5pt]
r_{\text{Kugel}}&=&\sqrt[3]{\dfrac{3}{4}\cdot \dfrac{523,6\,\text{cm}^3}{\pi}}\\[5pt]
r_{\text{Kugel}}&\approx&\boldsymbol{5,0\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/20a693667d94be5973f80c83104c66317a4537d04e78bf2d9ac4d526f593c3c2?color=5a5a5a) Der Radius beträgt
Der Radius beträgt  Höhe
Höhe  des entstandenen Körpers berechnen
des entstandenen Körpers berechnen
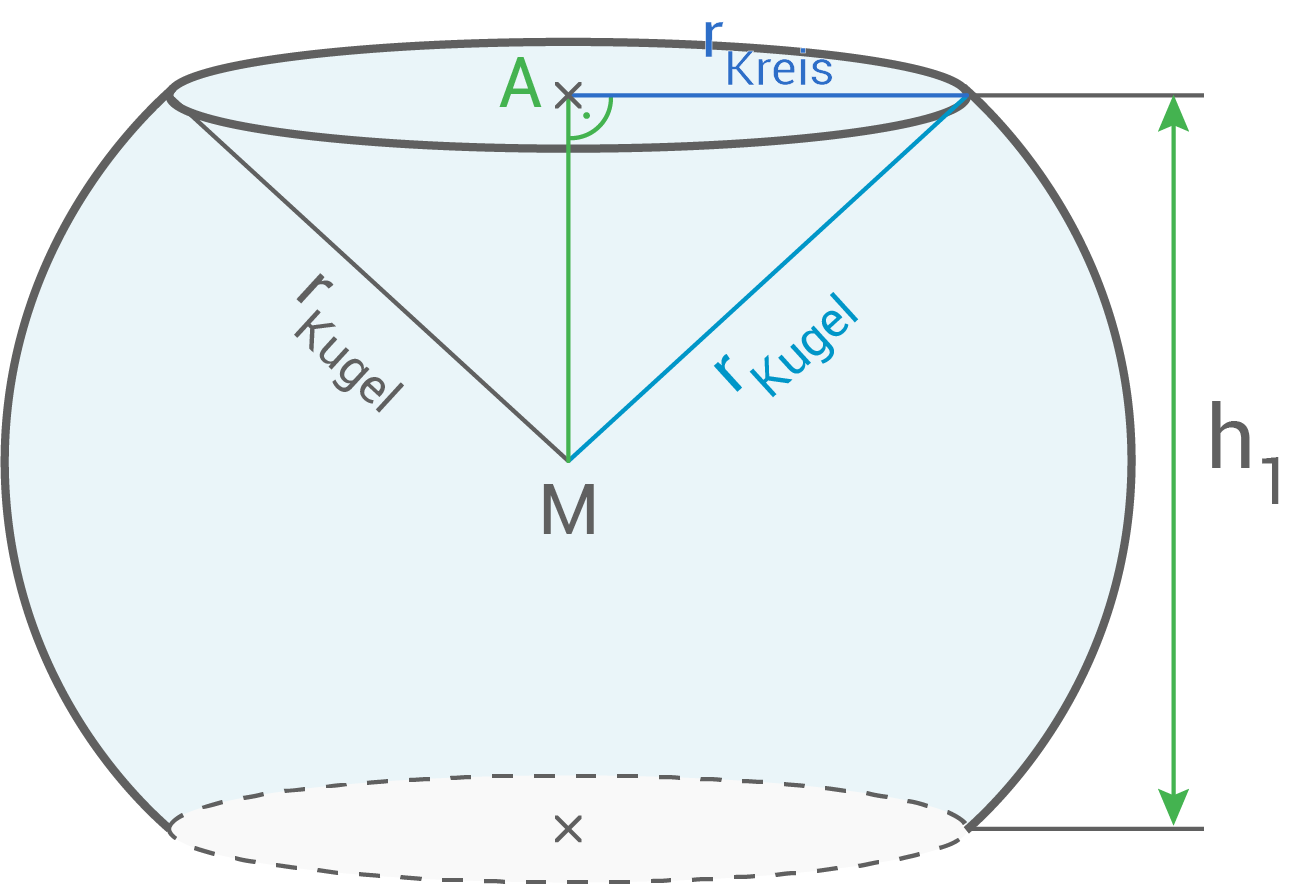
 berechnen
berechnen
![\(\begin{array}[t]{rll}
A&=&\pi\cdot r_{\text{Kreis}}^{\,\,\,\,\,\,\,\,\,\,2} &\quad \scriptsize \mid\;:\pi \\[5pt]
\dfrac{A}{\pi}&=&r_{\text{Kreis}}^{\,\,\,\,\,\,\,\,\,\,2} & \\[5pt]
r_{\text{Kreis}}^{\,\,\,\,\,\,\,\,\,\,2}&=&\dfrac{A}{\pi} &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
r_{\text{Kreis}}&=&\sqrt{\dfrac{A}{\pi}} \\[5pt]
r_{\text{Kreis}}&=&\sqrt{\dfrac{28,27\,\text{cm}^2}{\pi}} \\[5pt]
r_{\text{Kreis}}&\approx&3,00\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/fdc6d2635ede8f1affbb133784d5cbc43f3b97d2f31da89db55ad9344e071669?color=5a5a5a) Länge von
Länge von  mit dem Satz des Pythagoras berechnen
mit dem Satz des Pythagoras berechnen
![\(\begin{array}[t]{rll}
\overline{AM}^2+r_{\text{Kreis}}^{\,\,\,\,\,\,\,\,\,\,2}&=&r_{\text{Kugel}}^{\,\,\,\,\,\,\,\,\,\,2} \quad\quad\quad\quad\quad\quad \scriptsize \mid\;-r_{\text{Kreis}}^{\,\,\,\,\,\,2} \\[5pt]
\overline{AM}^2&=&r_{\text{Kugel}}^{\,\,\,\,\,\,\,\,\,\,2}-r_{\text{Kreis}}^{\,\,\,\,\,\,\,\,\,\,2} \quad\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
\overline{AM}&=&\sqrt{r_{\text{Kugel}}^{\,\,\,\,\,\,\,\,\,\,2}-r_{\text{Kreis}}^{\,\,\,\,\,\,\,\,\,\,2} }\\[5pt]
\overline{AM}&=&\sqrt{(5,0\,\text{cm})^2-(3,0\,\text{cm})^2}\\[5pt]
\overline{AM}&=&4\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/34b217c136637137c8f06c8f3bd361fda5ddb6f2faa72ab0c87f78007a4eb2d6?color=5a5a5a) Damit folgt für
Damit folgt für  :
:
![\(\begin{array}[t]{rll}
h_1&=&2\cdot \overline{AM} \\[5pt]
h_1&=&2\cdot4\,\text{cm}\\[5pt]
h_1&=&\boldsymbol{8\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/54f8d5afe1d7c83d368bbfc6578e5cbc00581bdb894cc5bc47a46b45ad6a4a53?color=5a5a5a) Die Höhe
Die Höhe  beträgt
beträgt  Höhe
Höhe  berechnen
berechnen
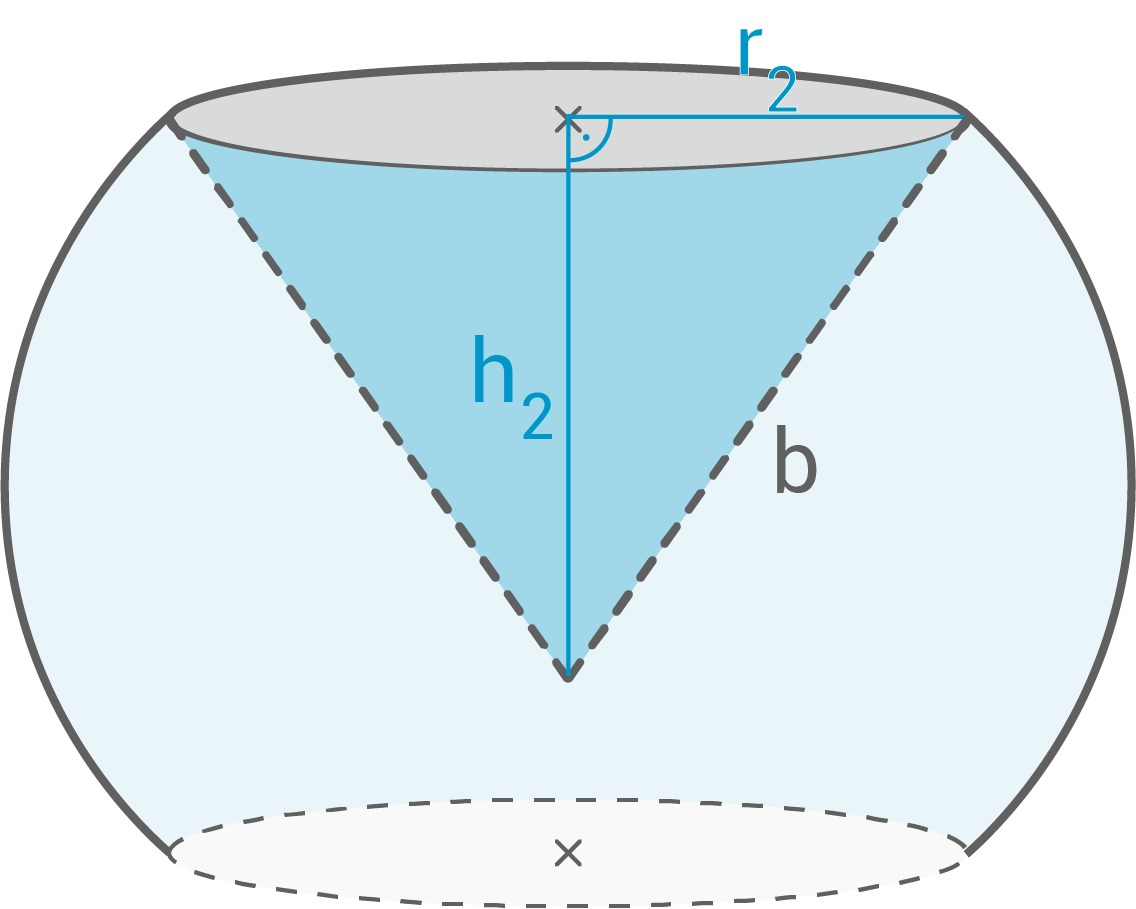 Satz des Pythagoras anwenden:
Satz des Pythagoras anwenden:
![\(\begin{array}[t]{rll}
r_2^2+h_2^2&=&b^2 &\quad \scriptsize \mid\;- r_2^2\\[5pt]
h_2^2&=&b^2-r_2^2 &\quad \scriptsize \mid\;\sqrt{\,\,}\\[5pt]
h_2&=&\sqrt{b^2-r_2^2} \\[5pt]
h_2&=&\sqrt{(10\,\text{cm})^2-(5,5\,\text{cm})^2} &\quad \scriptsize \mid\;\\[5pt]
h_2&\approx&\boldsymbol{8,35\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/b2b40a9d3074c6da88517eef148a8d90226d638c252f0c45ecd8dac688b099b4?color=5a5a5a) Die Höhe
Die Höhe  beträgt
beträgt 

