Wahlteil B
Aufgabe 1
a)
Der Würfel hat die Seitenlänge  .
.
Der Durchmesser der Grundfläche und die Höhe des Kegels entsprechen der Kantenlänge des Würfels.
( )
)
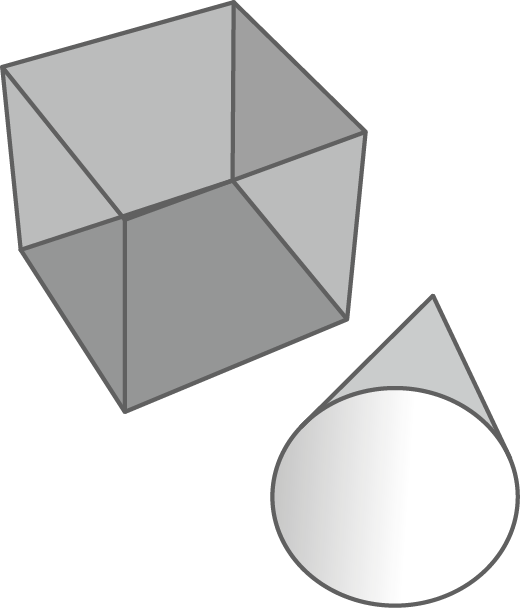
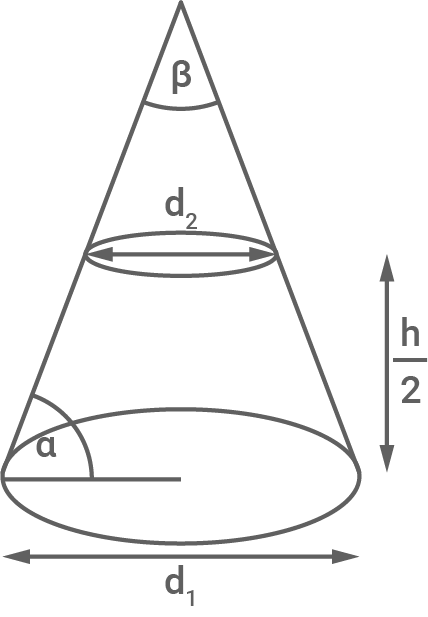

Der Durchmesser der Grundfläche und die Höhe des Kegels entsprechen der Kantenlänge des Würfels.
(


(Abbildung nicht maßstabsgetreu)
- Bestimme das Volumen des Kegels.
- Berechne den prozentualen Anteil des Kegelvolumens am Würfelvolumen.
- Bestimme den Winkel
oder
des Kegels.
- Überprüfe mithilfe des Strahlensatzes, ob diese Aussage richtig ist.
(5 Pkt.)
b)
In einem Beutel befinden sich insgesamt  Kugeln (rot, gelb und blau). Es werden
Kugeln (rot, gelb und blau). Es werden  Kugeln ohne Zurücklegen gezogen.
Wahrscheinlichkeit
Kugeln ohne Zurücklegen gezogen.
Wahrscheinlichkeit 
 und
und  .
.
 gold-,
gold-,  silber- und
silber- und  bronzefarbene Kugeln. Es wird zweimal mit Zurücklegen gezogen.
bronzefarbene Kugeln. Es wird zweimal mit Zurücklegen gezogen.
- Erstelle ein Baumdiagramm.
- Bestimme die Anzahl der roten, gelben und blauen Kugeln.
- Bestimme die Wahrscheinlichkeit, dass eine goldene und eine silberne Kugel gezogen werden. Die Reihenfolge spielt keine Rolle.
(5 Pkt.)
Aufgabe 2
a)
Gegeben ist die Parabel  .
.
 gespiegelt.
gespiegelt.
- Erstelle eine Wertetabelle im Bereich
.
- Zeichne die Parabel in ein geeignetes Koordinatensystem
- Bestimme die Funktionsgleichung der gespiegelten Parabel.
- Löse die Gleichung:
(5 Pkt.)
b)
Das Bild zeigt eine Kugel aus Bienenwachs, die Kugel ist innen hohl.
Das Volumen der Luft im Inneren der Kugel beträgt .
.
 .
.
 Bienenwachs wiegt
Bienenwachs wiegt  .
.
Das Volumen der Luft im Inneren der Kugel beträgt
- Berechne den inneren Durchmesser.
- Berechne das Gewicht des Bienenwachses in
.

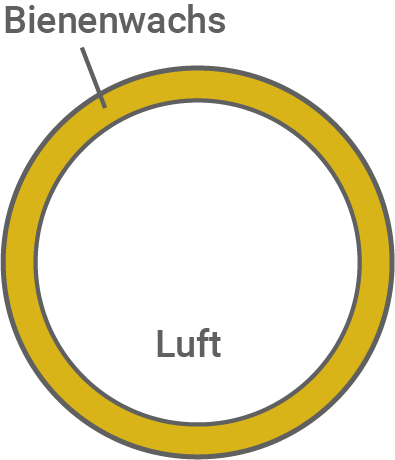
(Abbildung nicht maßstabsgetreu)
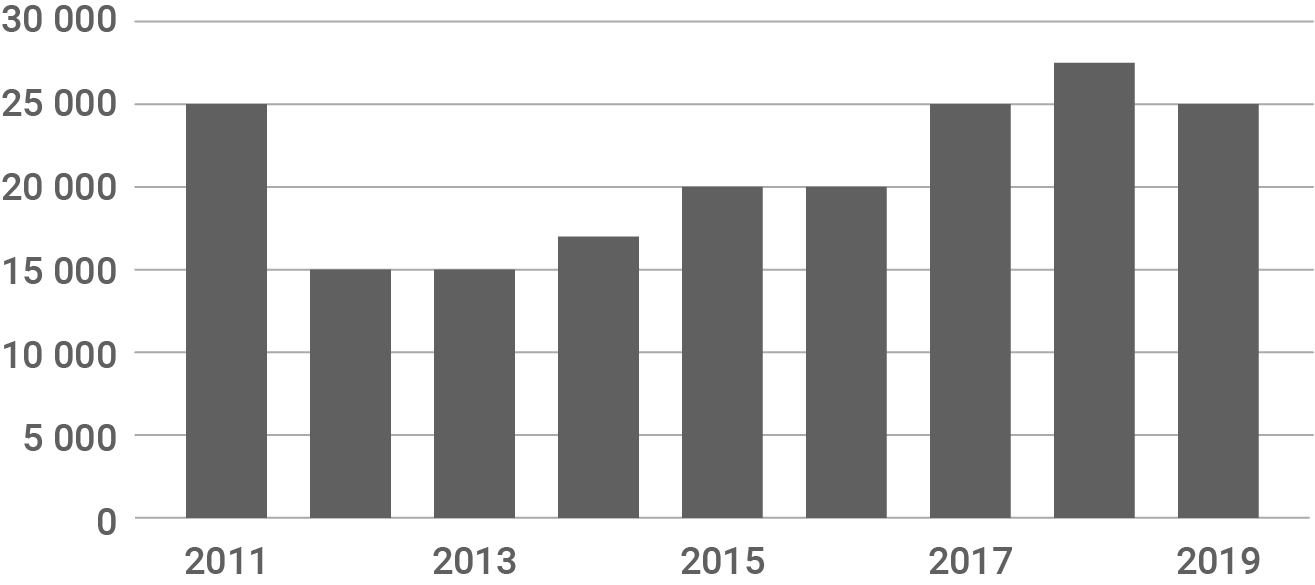
Honigproduktion in Deutschland (Angabe in Tonnen)
- Berechne die Menge an importiertem Honig in den Jahren
und
(5 Pkt.)
Aufgabe 3
a)
Ein Tangram ist ein Quadrat, das in  Teile geteilt wurde. Dabei entstehen
Teile geteilt wurde. Dabei entstehen  gleichschenklige Dreiecke, ein Quadrat und ein Parallelogramm.
In diesem Tangram haben die beiden großen Dreiecke jeweils einen Flächeninhalt von
gleichschenklige Dreiecke, ein Quadrat und ein Parallelogramm.
In diesem Tangram haben die beiden großen Dreiecke jeweils einen Flächeninhalt von  .
.
- Berechne die Seitenlänge
des gesamten Quadrates.
- Bestimme den jeweiligen prozentualen Anteil der Flächen
und
an der gesamten Fläche.
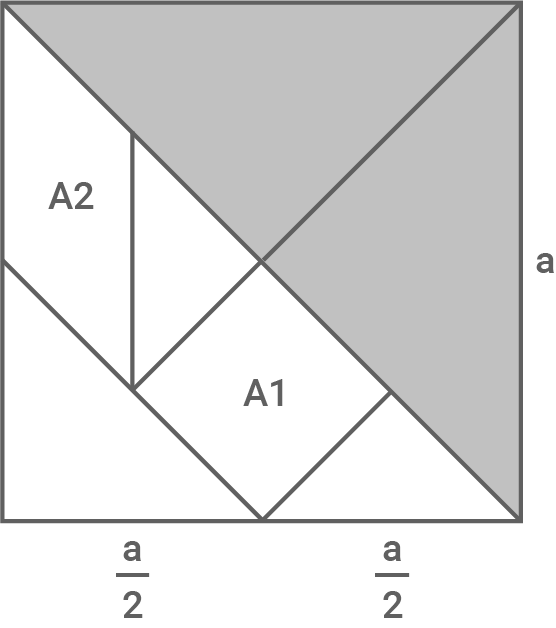
(Abbildung nicht maßstabsgetreu)
Eine kanadische Firma nutzt das Tangram auf einer Postkarte.
Die Herstellungskosten einer solchen Postkarte betragen
Die Firma verkauft die Karte für Darin enthalten sind
Darin enthalten sind  Mehrwertsteuer.
Mehrwertsteuer.
Die Herstellungskosten einer solchen Postkarte betragen
Die Firma verkauft die Karte für
- Berechne den Gewinn.

(5 Pkt.)
b)
Ein Rechteck hat einen Flächeninhalt von  .
.
Die lange Seite ist um länger als die kurze Seite.
länger als die kurze Seite.
„Wenn ich die beiden Seitenlängen eines Rechtecks verdopple, dann verdoppelt sich auch immer der Flächeninhalt des Rechtecks.“
Die lange Seite ist um
- Stelle eine Gleichung auf.
- Berechne die Seitenlängen des Rechtecks.
„Wenn ich die beiden Seitenlängen eines Rechtecks verdopple, dann verdoppelt sich auch immer der Flächeninhalt des Rechtecks.“
- Hat Merle recht? Begründe rechnerisch.
(5 Pkt.)
Aufgabe 4
a)
Herr Klausen legt  für drei Jahre an. Die Zinsen werden mitverzinst, der Zinssatz steigt mit jedem Jahr an. Im ersten Jahr wird seine Anlage mit
für drei Jahre an. Die Zinsen werden mitverzinst, der Zinssatz steigt mit jedem Jahr an. Im ersten Jahr wird seine Anlage mit  verzinst. Im zweiten Jahr werden ihm
verzinst. Im zweiten Jahr werden ihm  Zinsen gutgeschrieben. Nach Ablauf der drei Jahre hat er ein Guthaben von
Zinsen gutgeschrieben. Nach Ablauf der drei Jahre hat er ein Guthaben von  angespart.
angespart.
 bei der H-Bank an.
bei der H-Bank an.
 Jahren mindestens eine Wertsteigerung von
Jahren mindestens eine Wertsteigerung von  erzielen.
erzielen.
- Berechne die Zinssätze für das zweite und dritte Jahr.
- Stelle die jährlichen Zinsen in einem aussagekräftigen Diagramm dar.
| H-Bank | |
| Zinssatz: | |
|---|---|
| Laufzeit: | |
| Zinsen werden mitverzinst. | |
- Welchen Betrag bekommt Frau Bleich nach Ablauf von
Jahren ausbezahlt?
- Gelingt ihr dies? Begründe.
(5 Pkt.)
b)
Das Viereck hat einen Flächeninhalt von  .
.
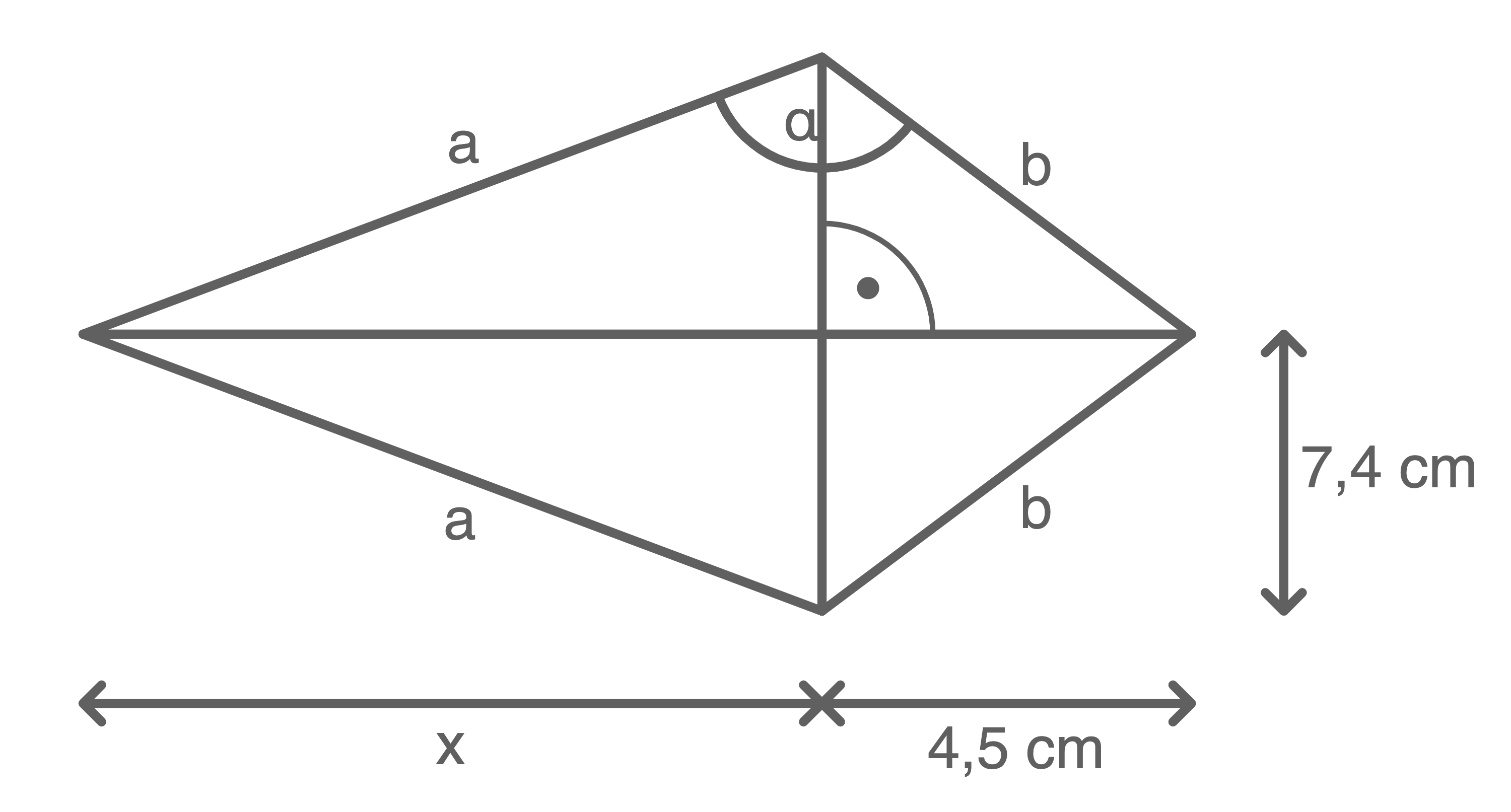
 .
.
Die beiden kurzen Seiten sind um kürzer als die langen.
kürzer als die langen.

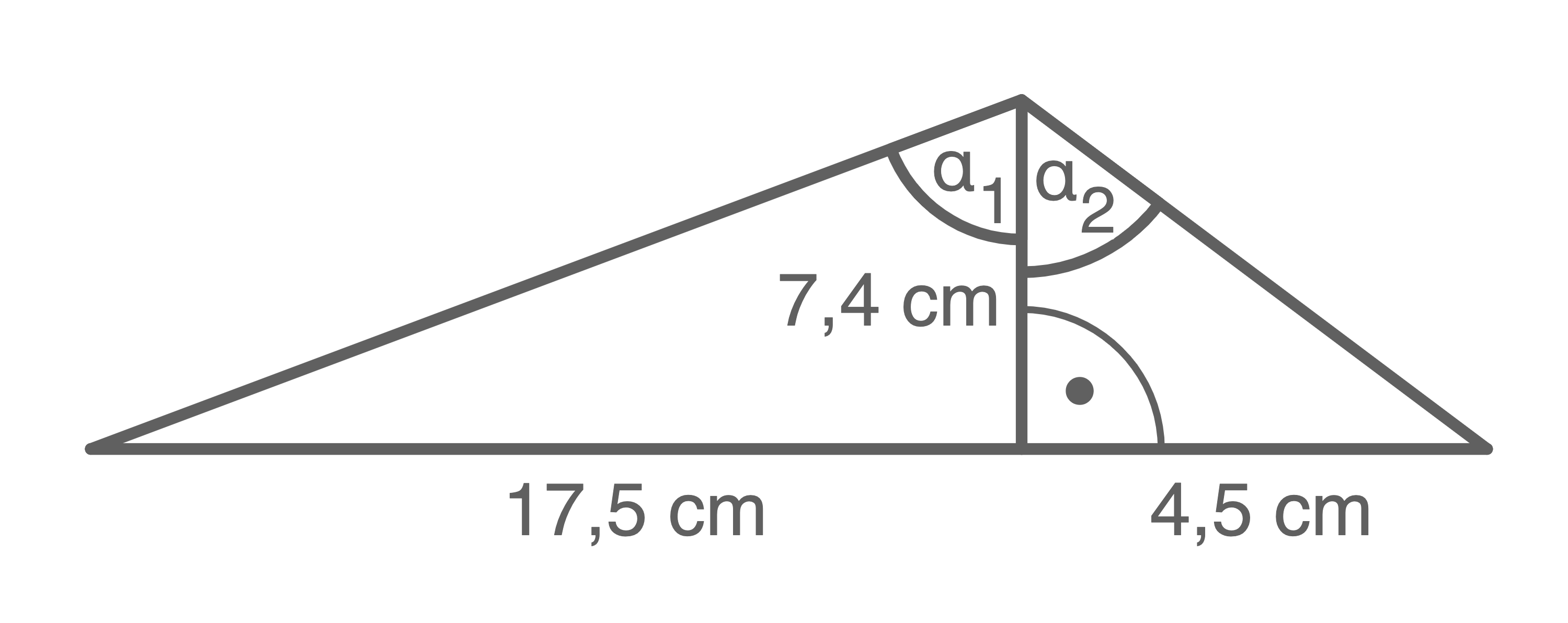
(Abbildung nicht maßstabsgetreu)
- Berechne
- Berechne den Winkel
Die beiden kurzen Seiten sind um
- Berechne die Längen
und
(5 Pkt.)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Kegelvolumen bestimmen


 Prozentualen Anteil berechnen
Prozentualen Anteil berechnen

 Anteil berechnen:
Anteil berechnen:
 Winkel bestimmen
Winkel bestimmen


 Mit Strahlensatz Aussage überprüfen
Mit Strahlensatz Aussage überprüfen
 Anstelle von
Anstelle von  kann auch
kann auch  geschrieben werden. Anstelle von
geschrieben werden. Anstelle von  entsprechend
entsprechend 
![\(\begin{array}[t]{rll}
h\cdot \dfrac{2}{h}&=&\dfrac{d_1}{2}\cdot \dfrac{2}{d_2}&\quad \scriptsize \mid\; \text{kürzen}\\[5pt]
2&=&\dfrac{d_1}{d_2}&\quad \scriptsize \mid\;\cdot d_2\\[5pt]
2\cdot d_2&=&d_1&\quad \scriptsize \mid\;:2\\[5pt]
d_2&=&\dfrac{d_1}{2}
\end{array}\)](https://mathjax.schullv.de/e36039e4732e6bc84a4402b39c305c1804e89c81ca7e542b57f5358249c40061?color=5a5a5a) Also ist die Aussage richtig.
Also ist die Aussage richtig.
b)
Baumdiagramm erstellen
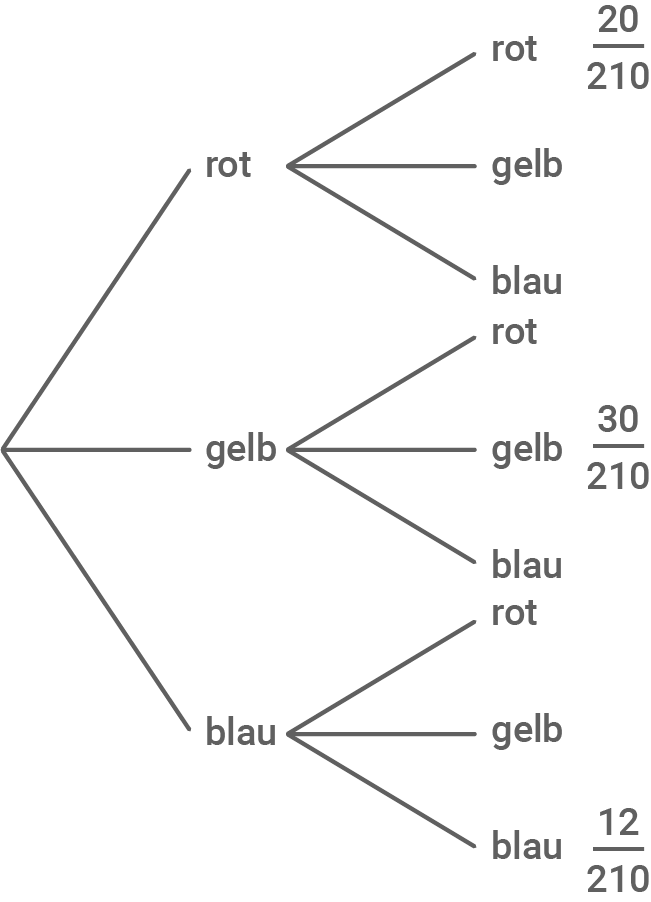 Anzahl Kugeln bestimmen
Anzahl rote Kugeln
Beim ersten Zug sind es insgesamt
Anzahl Kugeln bestimmen
Anzahl rote Kugeln
Beim ersten Zug sind es insgesamt  Kugeln, die Anzahl roter Kugeln ist dabei unbekannt. Also gilt:
Kugeln, die Anzahl roter Kugeln ist dabei unbekannt. Also gilt: 
Beim zweiten Zug sind es insgesamt noch Kugeln, die Anzahl verbleibender roter Kugeln ist dabei ebenfalls unbekannt. Also gilt:
Kugeln, die Anzahl verbleibender roter Kugeln ist dabei ebenfalls unbekannt. Also gilt:  Entlang einem Pfad gilt die Produktregel.
Entlang einem Pfad gilt die Produktregel.
![\(\begin{array}[t]{rll}
\dfrac{x}{15}\cdot \dfrac{x-1}{14}&=&\dfrac{20}{210} \\[5pt]
\dfrac{x\cdot (x-1)}{210}&=&\dfrac{20}{210} &\quad \scriptsize \mid\;\cdot 210 \\[5pt]
x\cdot (x-1)&=&20
\end{array}\)](https://mathjax.schullv.de/8e23081f3741476f52b55c00e044c2852d04d66d44a68894a32660bf28974c44?color=5a5a5a) Lösungsmöglichkeit A: Ausprobieren
Lösungsmöglichkeit A: Ausprobieren
 Lösungsmöglichkeit B: Berechnen
Zunächst wird die Gleichung in die Normalform gebracht:
Lösungsmöglichkeit B: Berechnen
Zunächst wird die Gleichung in die Normalform gebracht:
![\(\begin{array}[t]{rll}
x\cdot (x-1)&=&20 \,\,\scriptsize \;\text{Linke Seite ausmultiplizieren} \\[5pt]
x^2-x&=&20\,\,\scriptsize \;\mid\;-20\\[5pt]
x^2-x-20&=&0
\end{array}\)](https://mathjax.schullv.de/3cabe8c104903c335035c28d52342db94463519b384d38cca5fb65cc60fdedf4?color=5a5a5a) Lösungsformel anwenden:
Lösungsformel anwenden:
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-1}{2} \pm \sqrt{\left(\dfrac{-1}{2}\right)^2-(-20)} \\[5pt]
&=& \dfrac{1}{2} \pm \sqrt{\dfrac{1}{4}+20} \\[5pt]
&=& \dfrac{1}{2} \pm \sqrt{\dfrac{1}{4}+\dfrac{80}{4}} \\[5pt]
&=& \dfrac{1}{2} \pm \dfrac{9}{2} \\[5pt]
x_1&=&5\\[5pt]
x_2&=&-4\,(\text{keine Lösung})
\end{array}\)](https://mathjax.schullv.de/8bb99f4ec7bd75138f96ba2e4bd9a354ebc3cc956504eedbb0cc4daf6367dc96?color=5a5a5a) Es gibt
Es gibt  rote Kugeln.
Anzahl gelbe Kugeln
Beim ersten Zug sind es insgesamt
rote Kugeln.
Anzahl gelbe Kugeln
Beim ersten Zug sind es insgesamt  Kugeln, die Anzahl gelber Kugeln ist dabei unbekannt. Also gilt:
Kugeln, die Anzahl gelber Kugeln ist dabei unbekannt. Also gilt: 
Beim zweiten Zug sind es insgesamt noch Kugeln, die Anzahl verbleibender gelber Kugeln ist dabei ebenfalls unbekannt. Also gilt:
Kugeln, die Anzahl verbleibender gelber Kugeln ist dabei ebenfalls unbekannt. Also gilt:  Entlang einem Pfad gilt die Produktregel.
Entlang einem Pfad gilt die Produktregel.
![\(\begin{array}[t]{rll}
\dfrac{x}{15}\cdot \dfrac{x-1}{14}&=&\dfrac{30}{210} \\[5pt]
\dfrac{x\cdot (x-1)}{210}&=&\dfrac{30}{210} &\quad \scriptsize \mid\;\cdot 210 \\[5pt]
x\cdot (x-1)&=&30
\end{array}\)](https://mathjax.schullv.de/e6c480120829c0cd4015a09fe7de3ca1c4c447daec6dcc07331b74177ff41979?color=5a5a5a) Lösungsmöglichkeit A: Ausprobieren
Lösungsmöglichkeit A: Ausprobieren
 Lösungsmöglichkeit B: Berechnen
Zunächst wird die Gleichung in die Normalform gebracht:
Lösungsmöglichkeit B: Berechnen
Zunächst wird die Gleichung in die Normalform gebracht:
![\(\begin{array}[t]{rll}
x\cdot (x-1)&=&30 \,\,\scriptsize \;\text{Linke Seite ausmultiplizieren} \\[5pt]
x^2-x&=&30\,\,\scriptsize \;\mid\;-30\\[5pt]
x^2-x-30&=&0
\end{array}\)](https://mathjax.schullv.de/021c210a3e8585da1111f9b0417ecbaa55fffc1991af49009d0ccac1a24893ba?color=5a5a5a) Lösungsformel anwenden:
Lösungsformel anwenden:
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-1}{2} \pm \sqrt{\left(\dfrac{-1}{2}\right)^2-(-30)} \\[5pt]
&=& \dfrac{1}{2} \pm \sqrt{\dfrac{1}{4}+30} \\[5pt]
&=& \dfrac{1}{2} \pm \sqrt{\dfrac{1}{4}+\dfrac{120}{4}} \\[5pt]
&=& \dfrac{1}{2} \pm \dfrac{11}{2} \\[5pt]
x_1&=&6\\[5pt]
x_2&=&-5\,(\text{keine Lösung})
\end{array}\)](https://mathjax.schullv.de/2356ab9fa732b2599e0ee1fe04f2e36f6f5f033def8e1813734396aeccc67d2b?color=5a5a5a) Es gibt
Es gibt  gelbe Kugeln.
Anzahl blaue Kugeln
gelbe Kugeln.
Anzahl blaue Kugeln
 Es gibt
Es gibt  blaue Kugeln.
Wahrscheinlichkeit bestimmen
Es befinden sich
blaue Kugeln.
Wahrscheinlichkeit bestimmen
Es befinden sich  Kugeln im Beutel.
Kugeln im Beutel.


![\(\begin{array}[t]{rll}
P(\text{G. & S.})&=&\dfrac{26}{58}\cdot \dfrac{13}{58}+\dfrac{13}{58}\cdot \dfrac{26}{58}\\[5pt]
P(\text{G. & S.})&\approx&0,20
\end{array}\)](https://mathjax.schullv.de/6db7f9137ad11790bcb3d7a5d37f2fd43a744e7fef3ea5bbb2d2908c3f6bc082?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  wird eine goldene und eine silberne Kugel gezogen.
wird eine goldene und eine silberne Kugel gezogen.

Beim zweiten Zug sind es insgesamt noch
Beim zweiten Zug sind es insgesamt noch
Lösung 2
a)
Wertetabelle erstellen
Parabel zeichnen
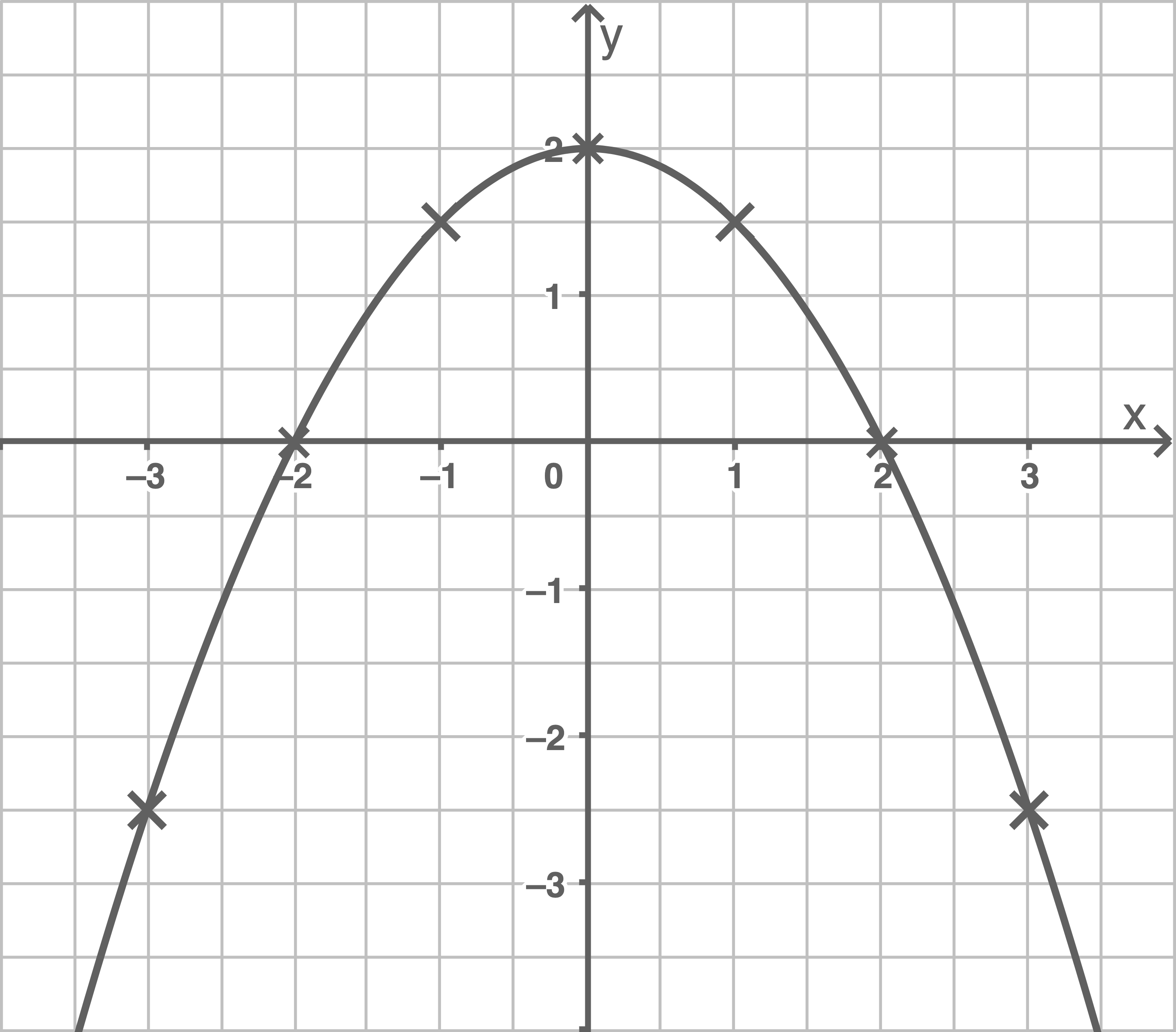 Funktionsgleichung bestimmen
Der Abstand vom Scheitelpunkt zur Geraden
Funktionsgleichung bestimmen
Der Abstand vom Scheitelpunkt zur Geraden  beträgt
beträgt  Also hat der neue Scheitelpunkt die Koordinaten
Also hat der neue Scheitelpunkt die Koordinaten  Die gespiegelte Parabel ist zudem nach oben geöffnet, es gilt also
Die gespiegelte Parabel ist zudem nach oben geöffnet, es gilt also 
 Gleichung lösen
Gleichung lösen
![\(\begin{array}[t]{rll}
2x-4&=&-2x^2+8 &\scriptsize \mid\;+2x^2-8 \\[5pt]
2x-12+2x^2&=&0 &\scriptsize \mid\;:2 \\[5pt]
x^2+x-6&=&0\\[5pt]
\end{array}\)](https://mathjax.schullv.de/bb762e90266491894b810dbce9150a50a6abedd8c56d56fdf5056210eaad91bd?color=5a5a5a) Lösen mit der Lösungsformel:
Lösen mit der Lösungsformel:
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{1}{2} \pm \sqrt{\left(\dfrac{1}{2}\right)^2-(-6)} \\[5pt]
&=& -\dfrac{1}{2} \pm \sqrt{\dfrac{1}{4}+6} \\[5pt]
&=& -\dfrac{1}{2} \pm \sqrt{\dfrac{1}{4}+\dfrac{24}{4}} \\[5pt]
&=& -\dfrac{1}{2} \pm \sqrt{\dfrac{25}{4}} \\[5pt]
&=& -\dfrac{1}{2} \pm \dfrac{5}{2}\\[5pt]
x_1&=& 2\\[5pt]
x_2&=& -3\\[5pt]
\end{array}\)](https://mathjax.schullv.de/86824c170268353d7e4115cecb40ee158db41a09e234a89b6a41fdd990c58bfd?color=5a5a5a)

b)
Inneren Durchmesser berechnen
Das Volumen einer Kugel wird über  berechnet.
Es gilt:
berechnet.
Es gilt: 
![\(\begin{array}[t]{rll}
\dfrac{4}{3}\cdot \pi\cdot r^3&=&998\,306\,\text{cm}^3 &\quad \scriptsize \mid\;:\left(\dfrac{4}{3}\pi\right) \\[5pt]
r^3&=&\dfrac{998\,306\,\text{cm}^3}{\frac{4}{3}\pi} &\quad \scriptsize \mid\;\sqrt[3]{\,\,} \\[5pt]
r&\approx&62\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/fb127b2d2100dfb83ae41b2d70117b19f2b62af0576fdaca9e1d2194143d4bcf?color=5a5a5a)
 Gewicht berechnen
1. Schritt: Volumen der äußeren Kugel berechnen
Gewicht berechnen
1. Schritt: Volumen der äußeren Kugel berechnen

 2. Schritt: Volumen des Bienenwachses berechnen
3. Schritt: Gewicht des Bienenwachses berechnen
2. Schritt: Volumen des Bienenwachses berechnen
3. Schritt: Gewicht des Bienenwachses berechnen

 Menge an importiertem Honig berechnen
Wenn
Menge an importiertem Honig berechnen
Wenn  des Honigs aus Deutschland kommen, dann werden
des Honigs aus Deutschland kommen, dann werden  importiert.
importiert.




![\(\begin{array}{rcl}
15\,000\,\text{t} & \mathrel{\widehat{=}}& 20\,\%\\[5pt]
750\,\text{t} & \mathrel{\widehat{=}}& 1\,\%\\[5pt]
60\,000\,\text{t} & \mathrel{\widehat{=}}& 80\,\%
\end{array}\)](https://mathjax.schullv.de/ce4d34bdde7bc423bb6c7d288e0bf0086ebc246d069fb8bbeb9fb34077ced11d?color=5a5a5a)



 2012 wurden also
2012 wurden also  Tonnen Honig importiert.
Tonnen Honig importiert.




![\(\begin{array}{rcl}
27\,500\,\text{t} & \mathrel{\widehat{=}}& 20\,\%\\[5pt]
1\,375\,\text{t} & \mathrel{\widehat{=}}& 1\,\%\\[5pt]
110\,000\,\text{t} & \mathrel{\widehat{=}}& 80\,\%
\end{array}\)](https://mathjax.schullv.de/fecff30eb8cdafda75f21d257903502bc1ffa0c16b8892c7d4d526e1fa37bd69?color=5a5a5a)



 2018 wurden also
2018 wurden also  Tonnen Honig importiert.
Tonnen Honig importiert.
Lösung 3
a)
Seitenlänge berechnen
Der Flächeninhalt eines der beiden großen Dreiecke beträgt:
 Da
Da  ist, gilt:
ist, gilt: 
![\(\begin{array}[t]{rll}
\dfrac{a^2}{4}&=&36\,\text{cm}^2 &\quad \scriptsize \mid\;\cdot 4 \\[5pt]
a^2&=&144\,\text{cm}^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
a&=&12\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/373d04cc1ff189fb0f7251b98c3c8f05ead181440dbb431bcbf72ea90f6bf303?color=5a5a5a) Prozentualen Anteil bestimmen
Prozentualen Anteil von A1 berechnen
Die Diagonale der Fläche A1 hat die Länge
Prozentualen Anteil bestimmen
Prozentualen Anteil von A1 berechnen
Die Diagonale der Fläche A1 hat die Länge  Die Seitenlänge des kleineren Quadrats wird mit
Die Seitenlänge des kleineren Quadrats wird mit  bezeichnet.
bezeichnet.
![\(\begin{array}[t]{rll}
b^2+b^2&=&(6\,\text{cm})^2\\[5pt]
2b^2&=&36\,\text{cm}^2 &\quad \scriptsize \mid\;:2 \\[5pt]
b^2&=&18\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/9ec3f5f4b7b6e9c8fa03ae48fd5654489b965c8b4181deb731517de50a530644?color=5a5a5a) Der Flächeninhalt von A1 beträgt also
Der Flächeninhalt von A1 beträgt also  und der Anteil damit:
und der Anteil damit:
 Prozentualen Anteil von A2 berechnen
Der Flächeninhalt von A2 beträgt
Prozentualen Anteil von A2 berechnen
Der Flächeninhalt von A2 beträgt  also einem Achtel der Gesamtfläche:
also einem Achtel der Gesamtfläche:
 Gewinn berechnen
Der Verkaufspreis ohne Mehrwertsteuer beträgt
Gewinn berechnen
Der Verkaufspreis ohne Mehrwertsteuer beträgt  Der Gewinn beträgt damit ca.
Der Gewinn beträgt damit ca.  pro Karte.
pro Karte.
b)
Gleichung aufstellen
 Seitenlängen berechnen
Seitenlängen berechnen
![\(\begin{array}[t]{rll}
b\cdot (b+4)&=&192\\[5pt]
b^2+4b&=&192 &\quad \scriptsize \mid\;-192 \\[5pt]
b^2+4b-192&=&0
\end{array}\)](https://mathjax.schullv.de/35fa04295a49aacd60a261487a62bdff74fdaf289c8c58c1664ce46671266698?color=5a5a5a) Mit der Lösungsformel wird
Mit der Lösungsformel wird  berechnet:
berechnet:
![\(\begin{array}[t]{rll}
b_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{4}{2} \pm \sqrt{\left(\dfrac{4}{2}\right)^2-(-192)} \\[5pt]
&=& -2 \pm \sqrt{4+192} \\[5pt]
&=& -2 \pm 14 \\[5pt]
b_1&=&12\\[5pt]
b_2&=&-16 \text{ (kann keine Länge sein)}
\end{array}\)](https://mathjax.schullv.de/7dcb15ee880a1f7a7cd6b73afad088ee33428eca7f7a482ccbadba5882348d83?color=5a5a5a)
 Das Rechteck hat also die Seitenlängen
Das Rechteck hat also die Seitenlängen  und
und  Begründen
Begründen

 Merle hat demnach nicht recht, da sich der Flächeninhalt vervierfacht.
Merle hat demnach nicht recht, da sich der Flächeninhalt vervierfacht.
Lösung 4
a)
Zinssätze berechnen


![\(\begin{array}[t]{rll}
K_2&=&K_1\cdot q_2 \\[5pt]
8\,164,80\,€&=&8\,064\,€\cdot q_2 & \scriptsize \mid\;:8\,064\,€ \\[5pt]
1,0125&=&q_2
\end{array}\)](https://mathjax.schullv.de/833a371e892d255adef2c136383d42d3923771ffed20ccf08d957a778a17a4d1?color=5a5a5a) Im zweiten Jahr beträgt der Zinssatz also
Im zweiten Jahr beträgt der Zinssatz also 

![\(\begin{array}[t]{rll}
K_3&=&K_2\cdot q_3 \\[5pt]
8\,368,92\,€&=&8\,164,80\,€\cdot q_3 & \scriptsize \mid\;:8\,164,80\,€ \\[5pt]
1,025&=&q_3
\end{array}\)](https://mathjax.schullv.de/b6fc4a37bddcadfe76d4f7b58cc9ee45d4c5eb66a816224c0c8a235d9198358e?color=5a5a5a) Im dritten Jahr beträgt der Zinssatz also
Im dritten Jahr beträgt der Zinssatz also  Jährliche Zinsen darstellen
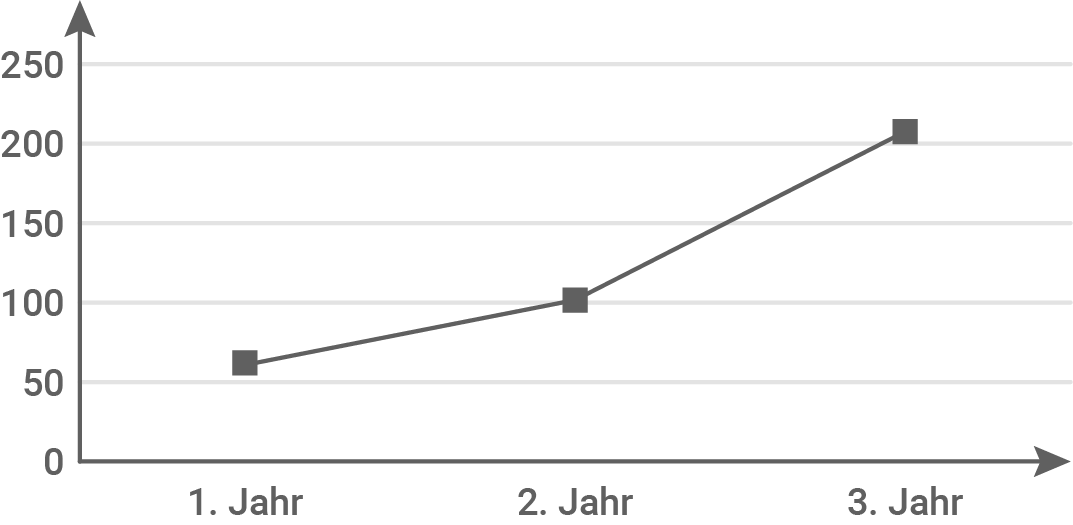
Darstellung z.B. als Liniendiagramm:
Zinsen 1. Jahr:
Jährliche Zinsen darstellen
Darstellung z.B. als Liniendiagramm:
Zinsen 1. Jahr: 
Zinsen 2. Jahr:
Zinsen 3. Jahr:

 Betrag bestimmen
Betrag bestimmen

 Frau Bleich bekommt also
Frau Bleich bekommt also  ausbezahlt.
Begründen
ausbezahlt.
Begründen

 Es gelingt ihr also.
Es gelingt ihr also.
Zinsen 2. Jahr:
Zinsen 3. Jahr:

b)
Länge von  berechnen
Der Flächeninhalt des halben Vierecks beträgt
berechnen
Der Flächeninhalt des halben Vierecks beträgt  Die Grundseite des halben Vierecks hat eine Länge von
Die Grundseite des halben Vierecks hat eine Länge von  und eine Höhe von
und eine Höhe von 
![\(\begin{array}[t]{rll}
\dfrac{(x+4,5)\cdot 7,4}{2}&=&81,4 & \scriptsize \mid\;\cdot 2 \\[5pt]
(x+4,5)\cdot 7,4&=&162,8 & \scriptsize \mid\;:7,4 \\[5pt]
x+4,5&=&22& \scriptsize \mid\;-4,5\\[5pt]
x&=&17,5
\end{array}\)](https://mathjax.schullv.de/29d9f9ee67456120e915bf91c7973ef3bc004ec20d0cd6c1d632b690fd90f640?color=5a5a5a) Die Länge von
Die Länge von  beträgt
beträgt  Größe des Winkels
Größe des Winkels  berechnen
berechnen




 Längen berechnen
Längen berechnen
![\(\begin{array}[t]{rll}
2\cdot a+2\cdot b&=&25,16\,\text{cm}\\[5pt]
2\cdot a+2\cdot (0,7a)&=&25,16\,\text{cm}\\[5pt]
3,4\cdot a&=&25,16\,\text{cm}&\scriptsize \mid\;:3,4\\[5pt]
a&=&7,4\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/bc66681b486f7884133a61603e011b916a367da5c2569ac3fec8ac9f25b26aeb?color=5a5a5a)
 Das Parallelogramm hat also die Seitenlängen
Das Parallelogramm hat also die Seitenlängen  und
und 
