Pflichtteil A1
1.
Gegeben sind folgende Zufallsgeräte.
- Wie groß ist die Wahrscheinlichkeit, dass bei einem 20-seitigen Würfel (Zahlen von 1 bis 20) eine Zahl kleiner als sieben gewürfelt wird?
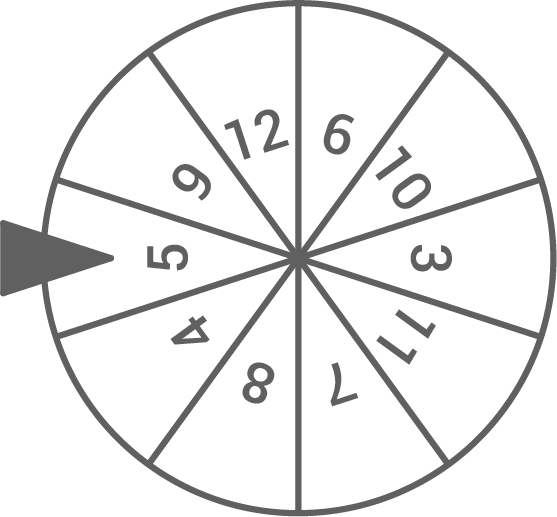
- Wie groß ist die Wahrscheinlichkeit, dass bei dem Glücksrad eine Primzahl gedreht wird?
(1 Pkt.)
3.
Immer zwei Zahlen haben den gleichen Wert.
- Gib den Zahlenwert an, der zu keinem anderen Zahlenwert passt.
(1 Pkt.)
4.
Das Diagramm zeigt das Ergebnis einer Befragung mit dem Titel „Dein Schulweg“.
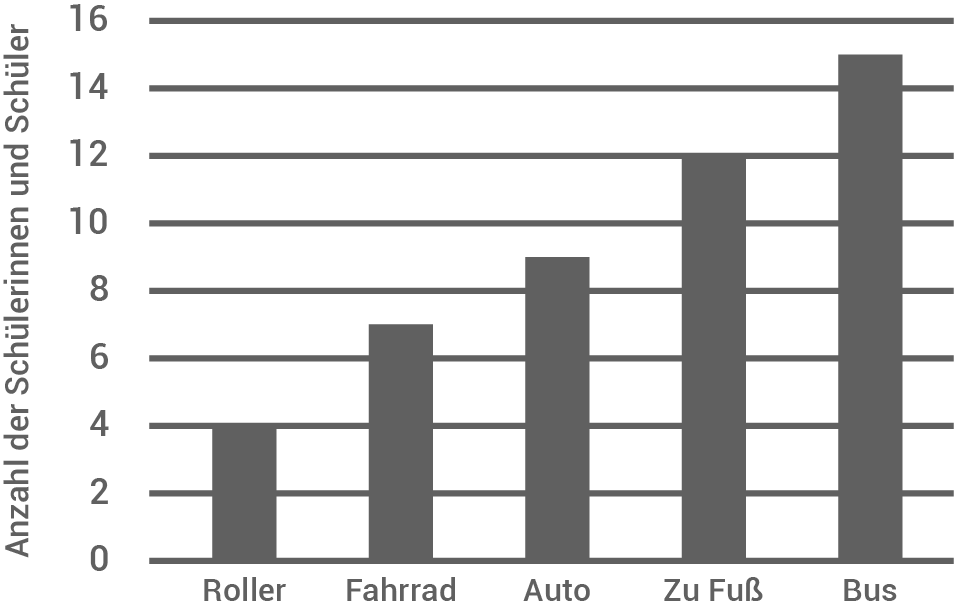Beschreibe, wie sich der Zentralwert verändert, wenn doppelt so viele Schülerinnen/Schüler mit dem Fahrrad zur Schule kommen und die Anzahl der anderen Nennungen gleich bleibt.
(1 Pkt.)
5.
Im gleichschenkligen Dreieck 
gilt: 
.
Die Gerade
verläuft parallel zur Strecke 
.
Berechne die Winkel
und 
Die Gerade
Berechne die Winkel
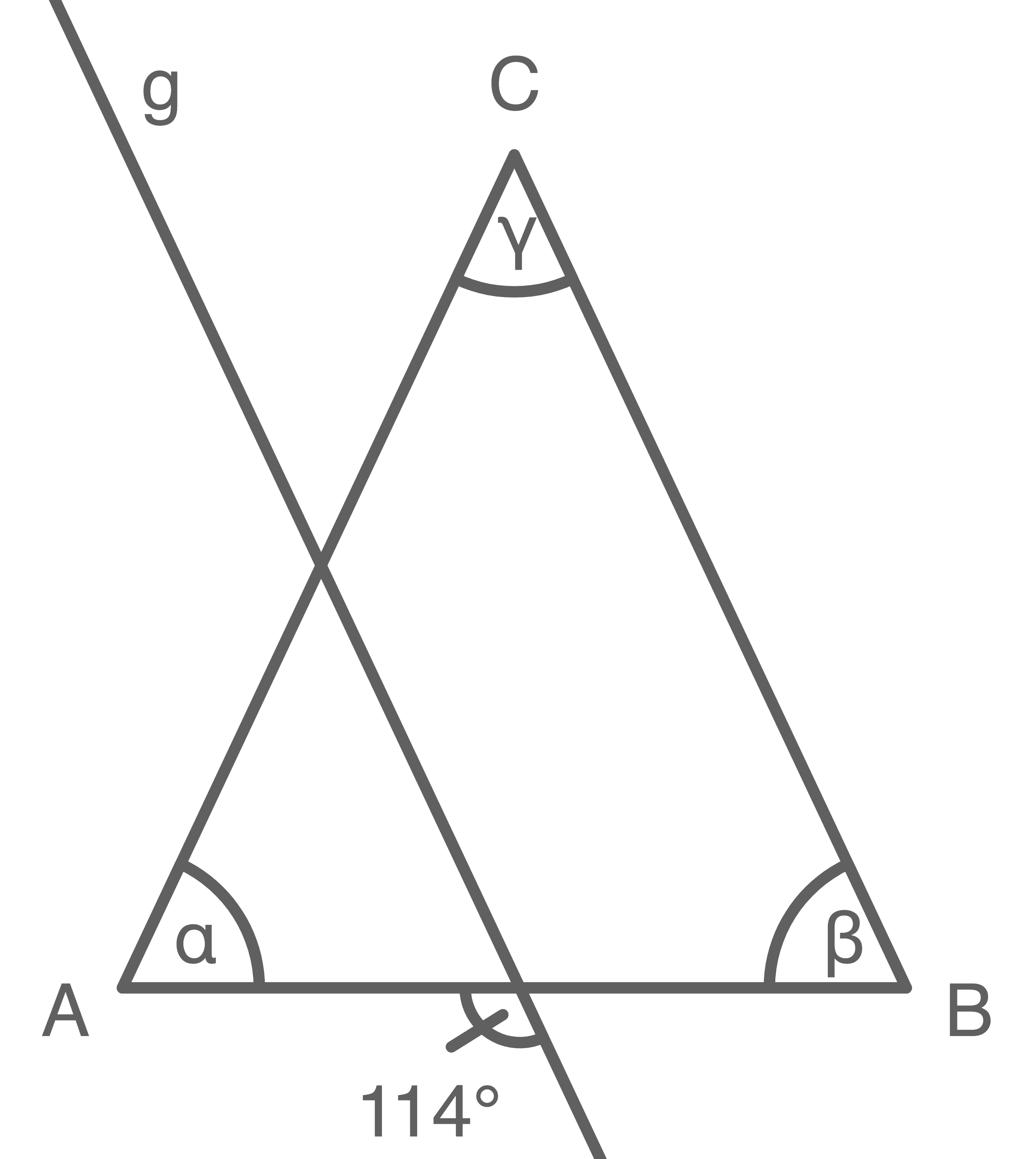
(Skizze nicht maßstabsgetreu)
(1 Pkt.)
6.
Am „Black Friday“ wird ein Tablet für 360,00 € angeboten. Der Preis wurde auf 80 % reduziert.
Bestimme den Preis des Tablets vor dem "Black Friday“.
(1 Pkt.)
7.
Bestimme die Anzahl der Lösungen der Gleichung.
(1 Pkt.)
8.
Eine Parabel 
ist im Vergleich zur Normalparabel
mithilfe der beschriebenen Eigenschaften an.
- um zwei Einheiten nach unten verschoben
- und mit dem Faktor drei gestreckt.
(1 Pkt.)
9.
Welcher der folgenden Terme passt nicht zur Oberfläche des zusammengesetzten Körpers? Kreuze an.
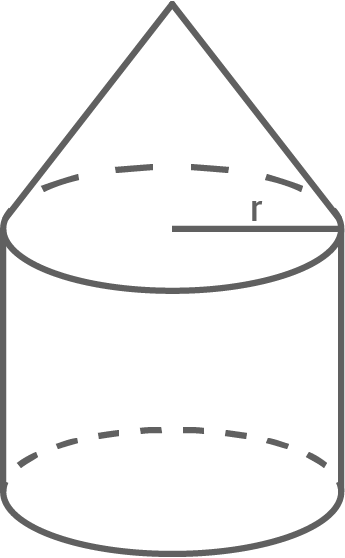
(1 Pkt.)
10.
In einer Eisdiele kann man sich ein Eis zusammenstellen.
Man kann zwischen einem Behältnis, einer Eissorte und einem Topping wählen.
Bestimme die Anzahl aller möglichen Kombinationen.
Man kann zwischen einem Behältnis, einer Eissorte und einem Topping wählen.
(1 Pkt.)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Wahrscheinlichkeit für eine Zahl kleiner als sieben
Von den 20 Zahlen auf dem Würfel sind 6 kleiner als 7.
Die Wahrscheinlichkeit, eine Zahl kleiner als sieben zu Würfeln, beträgt also 
Wahrscheinlichkeit für Primzahl beim Glücksrad
Von den 10 Zahlen auf dem Glücksrad sind 4 Primzahlen (3, 5, 7, 11).
Die Wahrscheinlichkeit, bei dem Rad eine Primzahl zu drehen, beträgt also 
2.
3.
4.
Zentralwert vor Verdopplung: 9
Zentralwert nach Verdopplung: 12
Der Zentralwert erhöht sich um 3.
5.
Da das Dreieck 
gleichschenklig ist und parallel zu verläuft, ist auch das kleine Dreieck links gleichschenklig. Damit folgt:
Da die Winkelsumme in einem Dreieck 
beträgt, gilt für den Winkel 
6.
7.
Es handelt sich um eine quadratische Gleichung, die zunächst umgeformt werden kann:
![\(\begin{array}[t]{rll}
2x^2+16x+25&=& -7 &\quad \scriptsize \mid\;+7 \\[5pt]
2x^2+16x+32&=& 0 &\quad \scriptsize \mid\;:2 \\[5pt]
x^2+8x+16&=& 0
\end{array}\)](https://mathjax.schullv.de/33f82eeab695f6f5161e9738458b9aa1ab91402a59db1d473516222fce930f44?color=5a5a5a)
Die Gleichung kann mit der Lösungsformel gelöst werden:
Dabei gilt 
und 
.
Für den Wert unter der Wurzel (die Diskriminante 
) gilt:
Da der Term unter der Wurzel gleich null ist, hat die Gleichung genau eine Lösung.
8.
9.
10.
Es gibt 
mögliche Kombinationen.