Pflichtteil A2
1.
Die Abbildung zeigt eine Bilderfolge aus Punkten.
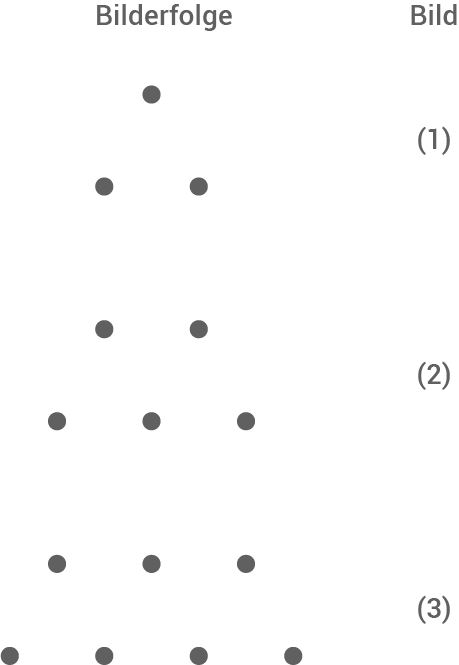

- Bestimme die Anzahl der Punkte im 11. Bild.
- Mit welchem Term kann man die Anzahl der Punkte im
ten Bild bestimmen? Begründe deine Entscheidung.
- Überprüfe, ob es ein Bild mit 45 Punkten gibt.
(3 Pkt.)
2.
Liam hat von seinem Opa zum Geburtstag 450,00 € geschenkt bekommen, die er sparen soll. Bei einer Bank bekommt er dafür 1,2 % Zinsen pro Jahr (Zinsen werden mitverzinst).
- Ergänze den Pfeil in der Tabelle durch den entsprechenden Faktor.
- Bestimme das Kapital nach 5 Jahren.
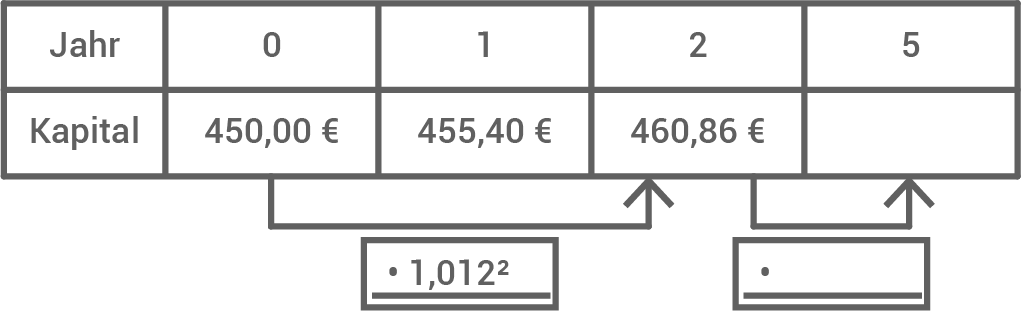
(2 Pkt.)
3.
Das dargestellte Körpernetz wird gefaltet und anschließend an den grauen Flächen miteinander verklebt.
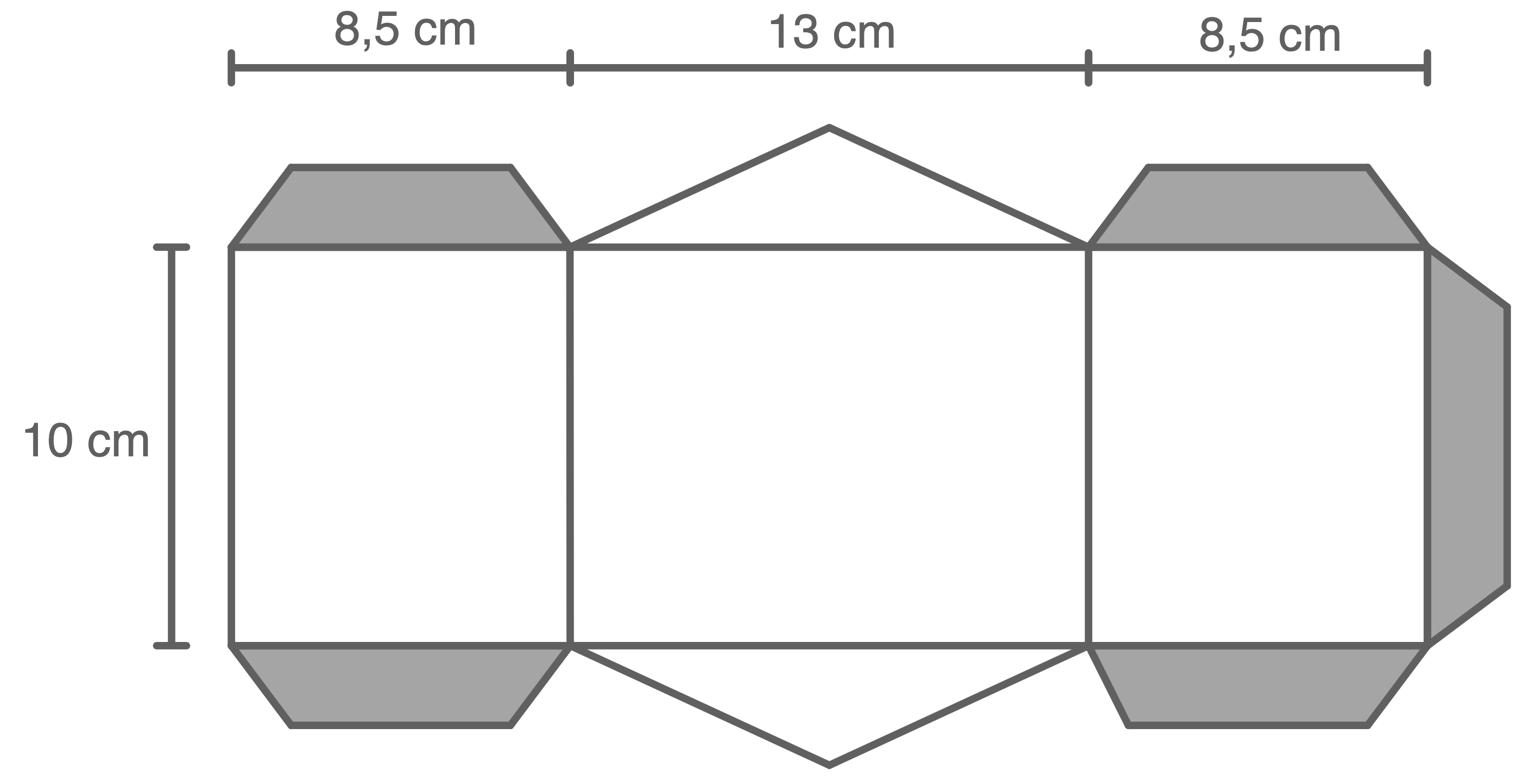
„Wenn man die Dreiecke der Grund- und Deckfläche an ihrer jeweils längsten Seite aneinanderlegt, erhält man eine Raute."

(Skizze nicht maßstabsgetreu)
- Berechne das Volumen des Körpers.
„Wenn man die Dreiecke der Grund- und Deckfläche an ihrer jeweils längsten Seite aneinanderlegt, erhält man eine Raute."
- Begründe deine Entscheidung.
(2 Pkt.)
4.
Die Parabel  hat die Funktionsgleichung
hat die Funktionsgleichung 
 -Werte verdoppelt, dann werden die
-Werte verdoppelt, dann werden die  -Werte
-Werte  “
(A) halbiert
“
(A) halbiert  (B) verdoppelt
(B) verdoppelt  (C) verdreifacht
(C) verdreifacht  (D) vervierfacht
Die Parabel
(D) vervierfacht
Die Parabel  wird zuerst um 4 LE nach oben verschoben und dann an der
wird zuerst um 4 LE nach oben verschoben und dann an der  -Achse gespiegelt.
-Achse gespiegelt.
- Untersuche die Parabel
und ergänze folgenden Satz mit dem richtigen Begriff.
- Gib die Funktionsgleichung für die neue Parabel
an.
(2 Pkt.)
5.
Von einem achsensymmetrischen Trapez sind die Koordinaten der Eckpunkte 
 und
und  gegeben.
gegeben.
 teilt das achsensymmetrische Trapez in zwei kongruente (deckungsgleiche) Dreiecke“. Hat er Recht?
teilt das achsensymmetrische Trapez in zwei kongruente (deckungsgleiche) Dreiecke“. Hat er Recht?
- Zeichne die Punkte in ein Koordinatensystem
und bestimme die Koordinaten des Punktes
- Bestimme den Flächeninhalt des Trapezes.
- Begründe deine Entscheidung.
(3 Pkt.)
6.
Familie König plant eine Fahrradtour. Ihre Route beträgt 135 km.
Sie planen mit einer durchschnittlichen Fahrgeschwindigkeit von 18 km/h.
Zusätzlich rechnen sie 2 Stunden für Pausen mit ein.
Die Familie möchte spätestens um 18 Uhr am Zielort sein.

Sie planen mit einer durchschnittlichen Fahrgeschwindigkeit von 18 km/h.
Zusätzlich rechnen sie 2 Stunden für Pausen mit ein.
Die Familie möchte spätestens um 18 Uhr am Zielort sein.
- Bestimme, um wie viel Uhr Familie König spätestens losfahren muss.
2 Erwachsene + 2 Kinder: 130 €
1 Erwachsener + 3 Kinder: 105 €

- Erstelle ein Gleichungssystem.
- Berechne die Preise für Erwachsene und Kinder.
(3 Pkt.)
7.
Ein Rechteck hat einen Flächeninhalt von 
Seite ist
ist  länger als Seite
länger als Seite 
Seite
- Bestimme die Länge der Diagonalen des Rechtecks.
(2 Pkt.)
8.
Ein Glücksrad hat folgende Eigenschaften:
- Die Gewinnwahrscheinlichkeit für die Farbe „Grün“ beträgt 30 %.
- Der „blaue“ Kreisausschnitt hat einen Winkel von 45°.
- Die „gelbe“ Farbe wird mit der Wahrscheinlichkeit von gedreht.
gedreht.
- Der restliche Teil des Glücksrads ist „rot".
- Der „blaue“ Kreisausschnitt hat einen Winkel von 45°.
- Die „gelbe“ Farbe wird mit der Wahrscheinlichkeit von
- Der restliche Teil des Glücksrads ist „rot".
- Zeichne das Glücksrad mit einem Radius von 5 cm.
- Berechne die Wahrscheinlichkeit des Ereignisses
(zuerst gelb, dann grün).
(3 Pkt.)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Anzahl der Punkte im 11. Bild bestimmen
Im 11. Bild sind 23 Punkte.
Passenden Term auswählen und begründen
Die Anzahl der Punkte im  -ten Bild kann durch Term
-ten Bild kann durch Term  beschrieben werden.
In der oberen Reihe befinden sich immer
beschrieben werden.
In der oberen Reihe befinden sich immer  Punkte und in der unteren
Punkte und in der unteren  Punkte. Insgesamt ergibt das
Punkte. Insgesamt ergibt das  Punkte.
Überprüfen, ob es ein Bild mit 45 Punkten gibt
Punkte.
Überprüfen, ob es ein Bild mit 45 Punkten gibt
![\(\begin{array}[t]{rll}
1+2x&=& 45 &\quad \scriptsize \mid\; -1 \\[5pt]
2x &=& 44 &\quad \scriptsize \mid\; :2 \\[5pt]
x &=& 22
\end{array}\)](https://mathjax.schullv.de/93edc2d9c8043fdef815f4a775b6fa668cc9c41deee9e857558997abd5de0564?color=5a5a5a) Das 22. Bild hat 45 Punkte.
Das 22. Bild hat 45 Punkte.
2.
Pfeil ergänzen
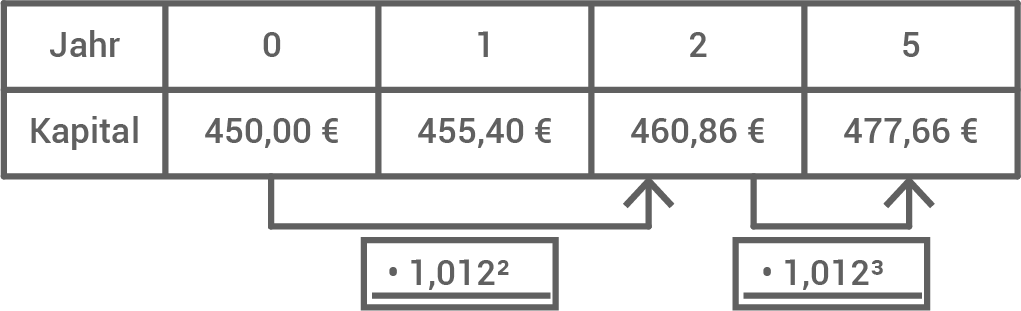 Kapital nach 5 Jahren bestimmen
Kapital nach 5 Jahren bestimmen


3.
Volumen des Körpers berechnen
1. Schritt: Höhe der dreieckigen Grundfläche berechnen
Mit dem Satz des Pythagoras gilt füt die Höhe  2. Schritt: Flächeninhalt der dreieckigen Grundfläche berechnen
2. Schritt: Flächeninhalt der dreieckigen Grundfläche berechnen
![\(\begin{array}[t]{rll}
G&=& \dfrac{1}{2}\cdot g\cdot h_D \\[5pt]
&\approx& \dfrac{1}{2}\cdot 13\,\text{cm}\cdot 5,48\,\text{cm} \\[5pt]
&=& 35,62\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/6337c161ad8c0cbca297c0617317c23d14a9cd8396e7b3e2f9d5982d86bc2431?color=5a5a5a) 3. Schritt: Volumen berechnen
Mit der Formel für das Volumen eines Prismas gilt:
3. Schritt: Volumen berechnen
Mit der Formel für das Volumen eines Prismas gilt:
![\(\begin{array}[t]{rll}
V&=& G\cdot h \\[5pt]
&\approx& 35,62\,\text{cm}^2\cdot 10\,\text{cm} \\[5pt]
&=& 356,20\,\text{cm}^3
\end{array}\)](https://mathjax.schullv.de/b8435a29cd3c2f7088bde74332d73abaae0537ae6218c4a6c8613c80bee4f6dc?color=5a5a5a) Aussage beurteilen und begründen
Die Aussage stimmt.
Aussage beurteilen und begründen
Die Aussage stimmt.
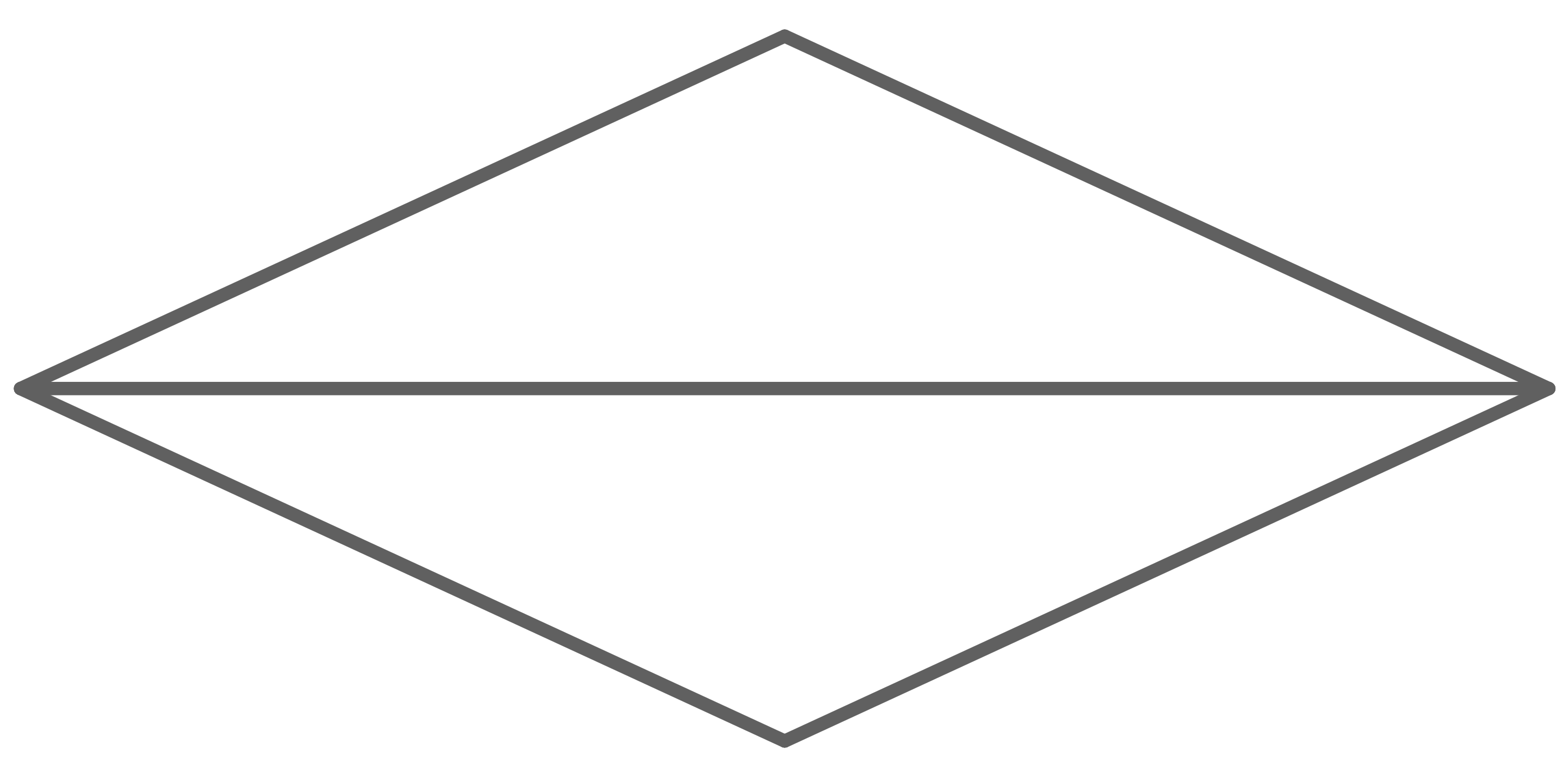 Da alle Seiten gleich lang, gegenüberliegende Seiten parallel und gegenüberliegende Winkel gleich groß sind, handelt es sich um eine Raute.
Da alle Seiten gleich lang, gegenüberliegende Seiten parallel und gegenüberliegende Winkel gleich groß sind, handelt es sich um eine Raute.

4.
Satz ergänzen
„Wenn man die  -Werte verdoppelt, dann werden die
-Werte verdoppelt, dann werden die  -Werte vervierfacht.“
Funktionsgleichung für
-Werte vervierfacht.“
Funktionsgleichung für  angeben
angeben

5.
Punkte einzeichnen und Koordinaten von  angeben
angeben
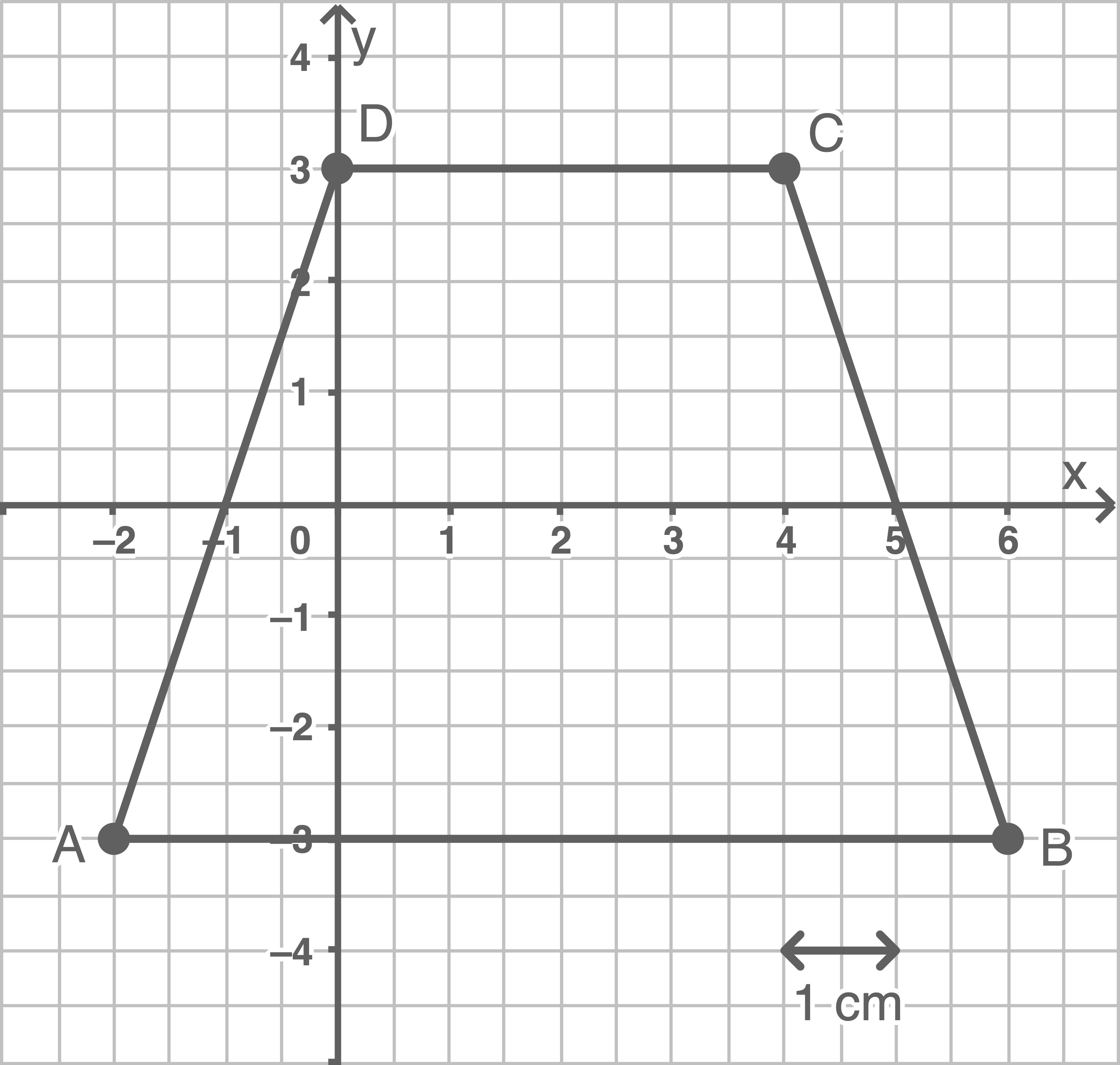 Der Punkt
Der Punkt  hat die Koordinaten
hat die Koordinaten  Flächeninhalt des Trapezes bestimmen
Höhe: 6 cm
Flächeninhalt des Trapezes bestimmen
Höhe: 6 cm
Länge untere Seite: 8 cm
Länge obere Seite: 4 cm Mit der Formel für den Flächeninhalt eines Trapezes folgt:![\(\begin{array}[t]{rll}
A&=& \dfrac{4\,\text{cm}+8\,\text{cm}}{2}\cdot 6\,\text{cm} \\[5pt]
&=& 36\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/600d19995ac44a2a5f74dfb7b96ebedf282f85acb9b9b36d17d0a73e23561e4f?color=5a5a5a) Behauptung beurteilen und begründen
Die Aussage ist falsch.
Die Gerade verläuft durch die Punkte
Behauptung beurteilen und begründen
Die Aussage ist falsch.
Die Gerade verläuft durch die Punkte  und
und  Ein Trapez ist an seiner Diagonalen jedoch nicht achsensymmetrisch. Daher können die beiden entstehenden Dreiecke nicht kongruent sein.
Ein Trapez ist an seiner Diagonalen jedoch nicht achsensymmetrisch. Daher können die beiden entstehenden Dreiecke nicht kongruent sein.

Länge untere Seite: 8 cm
Länge obere Seite: 4 cm Mit der Formel für den Flächeninhalt eines Trapezes folgt:
6.
Uhrzeit bestimmen
Fahrzeit berechnen:
 Mit den zusätzlichen 2 Stunden Pause muss Familie König spätestens 9,5 Stunden vor 18 Uhr losfahren. Das ist um 8:30 Uhr.
Gleichungssystem erstellen
Mit den zusätzlichen 2 Stunden Pause muss Familie König spätestens 9,5 Stunden vor 18 Uhr losfahren. Das ist um 8:30 Uhr.
Gleichungssystem erstellen
 Dabei gibt
Dabei gibt  den Preis für Erwachsene und
den Preis für Erwachsene und  den Preis für Kinder an.
Preise berechnen
Lösungsmöglichkeit A (Gleichsetzungsverfahren)
den Preis für Kinder an.
Preise berechnen
Lösungsmöglichkeit A (Gleichsetzungsverfahren)
 Beide Gleichungen werden nach
Beide Gleichungen werden nach  aufgelöst:
aufgelöst:


![\(\begin{array}[t]{rll}
65-y&=& 105-3y \quad \scriptsize \mid\; +3y\\[5pt]
65+2y&=& 105 \quad \scriptsize \mid\; -65\\[5pt]
2y&=& 40 \quad \scriptsize \mid\;:2\\[5pt]
y&=& 20
\end{array}\)](https://mathjax.schullv.de/4f78ec2da5333cec8fbb337444aac7575b543e2c1b917a12e8f7eb31063d338f?color=5a5a5a)
 in
in 
 Der Preis für Kinder beträgt 20 €, der für Erwachsene 45 €.
Lösungsmöglichkeit B (Einsetzungsverfahren)
Der Preis für Kinder beträgt 20 €, der für Erwachsene 45 €.
Lösungsmöglichkeit B (Einsetzungsverfahren)
 Zweite Gleichung nach
Zweite Gleichung nach  auflösen:
auflösen:
![\(\begin{array}[t]{rll}
\text{(II)}\quad x+3y&=& 105 \quad \scriptsize \mid\;-3y \\[5pt]
x&=& 105-3y
\end{array}\)](https://mathjax.schullv.de/a4df44bcb153446b22a767a0315ca99861649982fce5e4a9225175afd500d015?color=5a5a5a)
 in
in 
![\(\begin{array}[t]{rll}
2\cdot (105-3y)+2y&=& 130 \\[5pt]
210-4y&=& 130 \quad \scriptsize \mid\; -210\\[5pt]
-4y&=& -80 \quad \scriptsize \mid\; :(-4)\\[5pt]
y&=& 20
\end{array}\)](https://mathjax.schullv.de/8df966d0eb587f6458da509326d426948380343a59acf459e75e510d104b94f6?color=5a5a5a)
 in
in 
 Der Preis für Kinder beträgt 20 €, der für Erwachsene 45 €.
Der Preis für Kinder beträgt 20 €, der für Erwachsene 45 €.
7.
Seitenlängen des Rechtecks berechnen
Mit  folgt:
folgt:
![\(\begin{array}[t]{rll}
a\cdot b&=& 60 \\[5pt]
a\cdot (a-7)&=& 60\\[5pt]
a^2-7a&=& 60 \quad \scriptsize \mid\; -60\\[5pt]
a^2-7a-60&=& 0
\end{array}\)](https://mathjax.schullv.de/f16132abd0c2713f4856f4784fb52288a9a4368ab6df83f6b3e688a2eacc953a?color=5a5a5a) Lösungsformel anwenden:
Lösungsformel anwenden:
![\(\begin{array}[t]{rll}
a_{1,2}&=& -\dfrac{-7}{2}\pm\sqrt{\left(\dfrac{-7}{2}\right)^2-(-60)} \\[5pt]
&=& 3,5\pm 8,5\\[5pt]
a_1&=& 12\\[5pt]
a_2&=& -5
\end{array}\)](https://mathjax.schullv.de/94f4ef51fcabc3cba6a8572e3d96662a8bda94fe1afa8587a9bb406ffddd577e?color=5a5a5a) In diesem Kontext ist nur
In diesem Kontext ist nur  möglich. Daraus folgt
möglich. Daraus folgt  Das Rechteck hat also die Seitenlängen
Das Rechteck hat also die Seitenlängen  und
und  Länge der Diagonalen berechnen
Mit dem Satz des Pythagoras gilt:
Länge der Diagonalen berechnen
Mit dem Satz des Pythagoras gilt:
![\(\begin{array}[t]{rll}
d^2&=& (12\,\text{cm})^2+(5\,\text{cm})^2 \\[5pt]
d^2&=& 169\,\text{cm}^2 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt]
d&=& 13\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/ea214c6375caafbcf7b9981a5fc02ffd86baf330c36088c799e8b513316de559?color=5a5a5a) Die Diagonale des Rechtecks ist 13 cm lang.
Die Diagonale des Rechtecks ist 13 cm lang.
8.
Glücksrad zeichnen
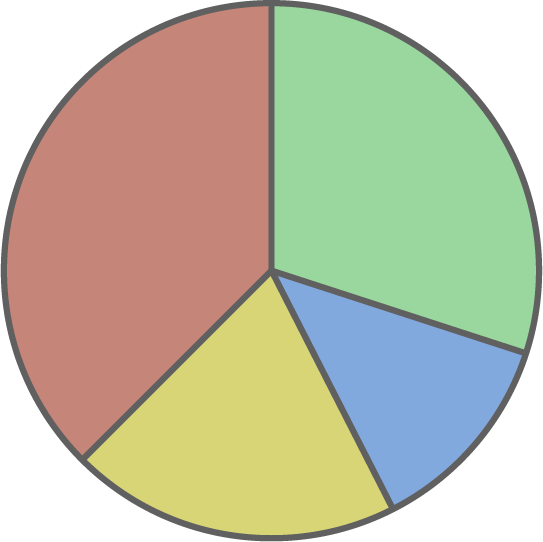 Hinweis: Die Länge des Radius kann je nach Bildschirmgröße variieren.
Grün:
Hinweis: Die Länge des Radius kann je nach Bildschirmgröße variieren.
Grün:  Gelb:
Gelb:  Rot:
Rot:  Wahrscheinlichkeit berechnen
Wahrscheinlichkeit berechnen


