Grundkenntnisse
1.
Löse die Gleichung:
(1 Pkt.)
2.
Berechne die Strecke 
.
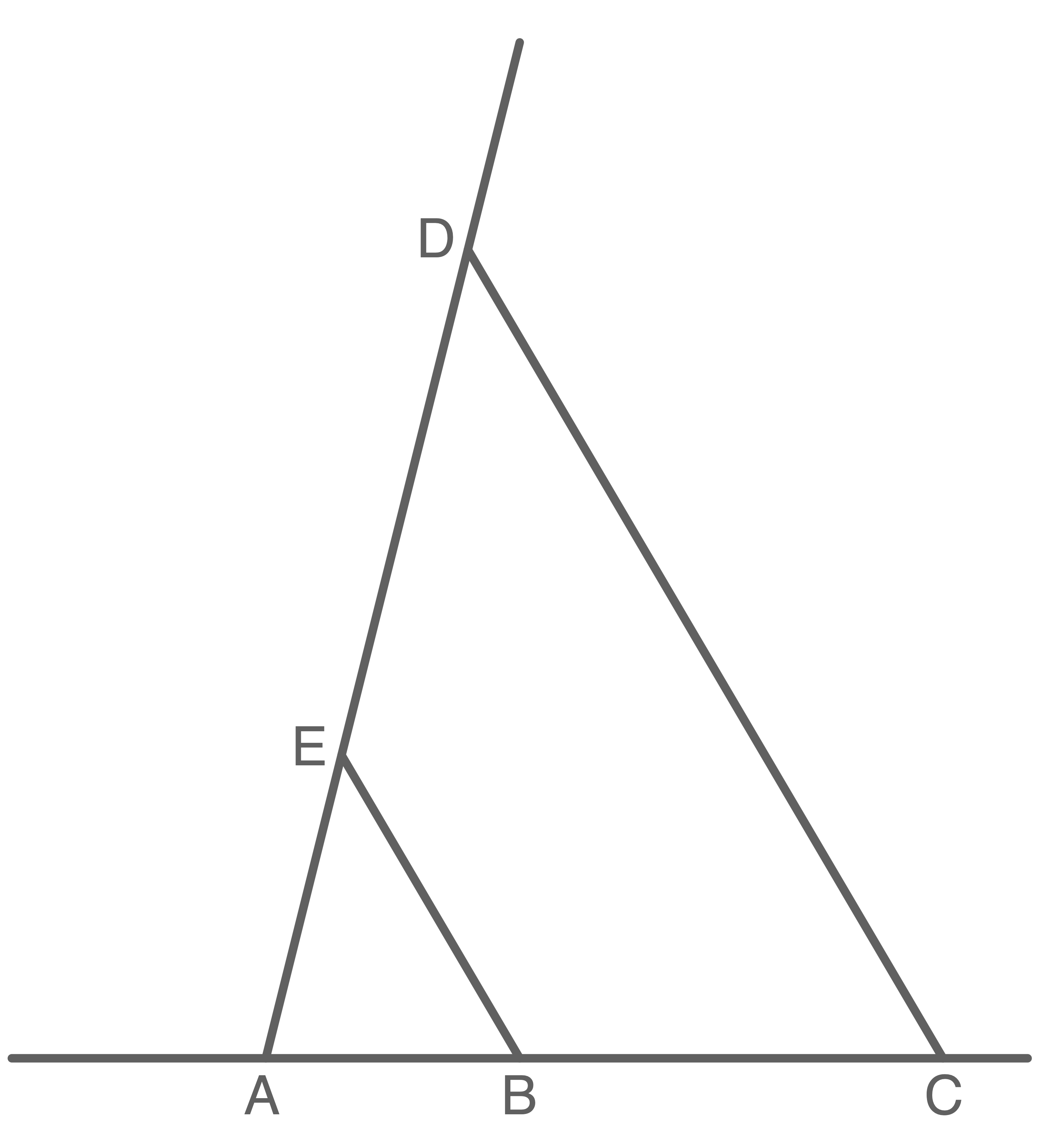
(Skizze nicht maßstabsgetreu)
(1 Pkt.)
3.
Ein Kegel mit 
hat ein Volumen von 
Überprüfe folgende Behauptung: Das Volumen einer Kugel mit gleichem Radius beträgt das Dreifache des Kegelvolumens.
(1 Pkt.)
4.
Benenne die richtige Funktionsgleichung zur Geraden 
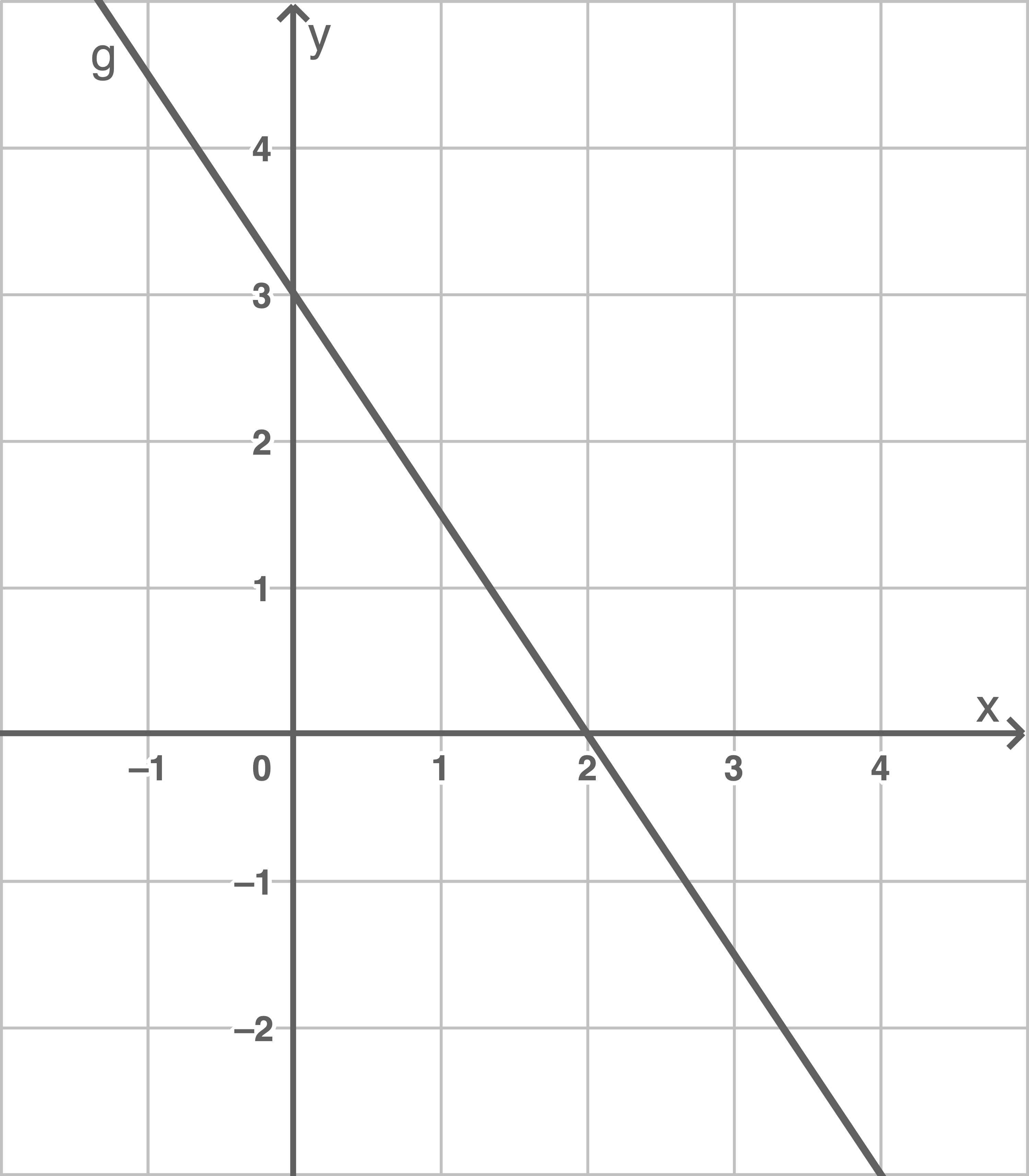
(A) 
(B)
(C)
(D)
(B)
(C)
(D)
(1 Pkt.)
5.
Löse das Gleichungssystem.
(1 Pkt.)
6.
Berechne die Strecke 
.
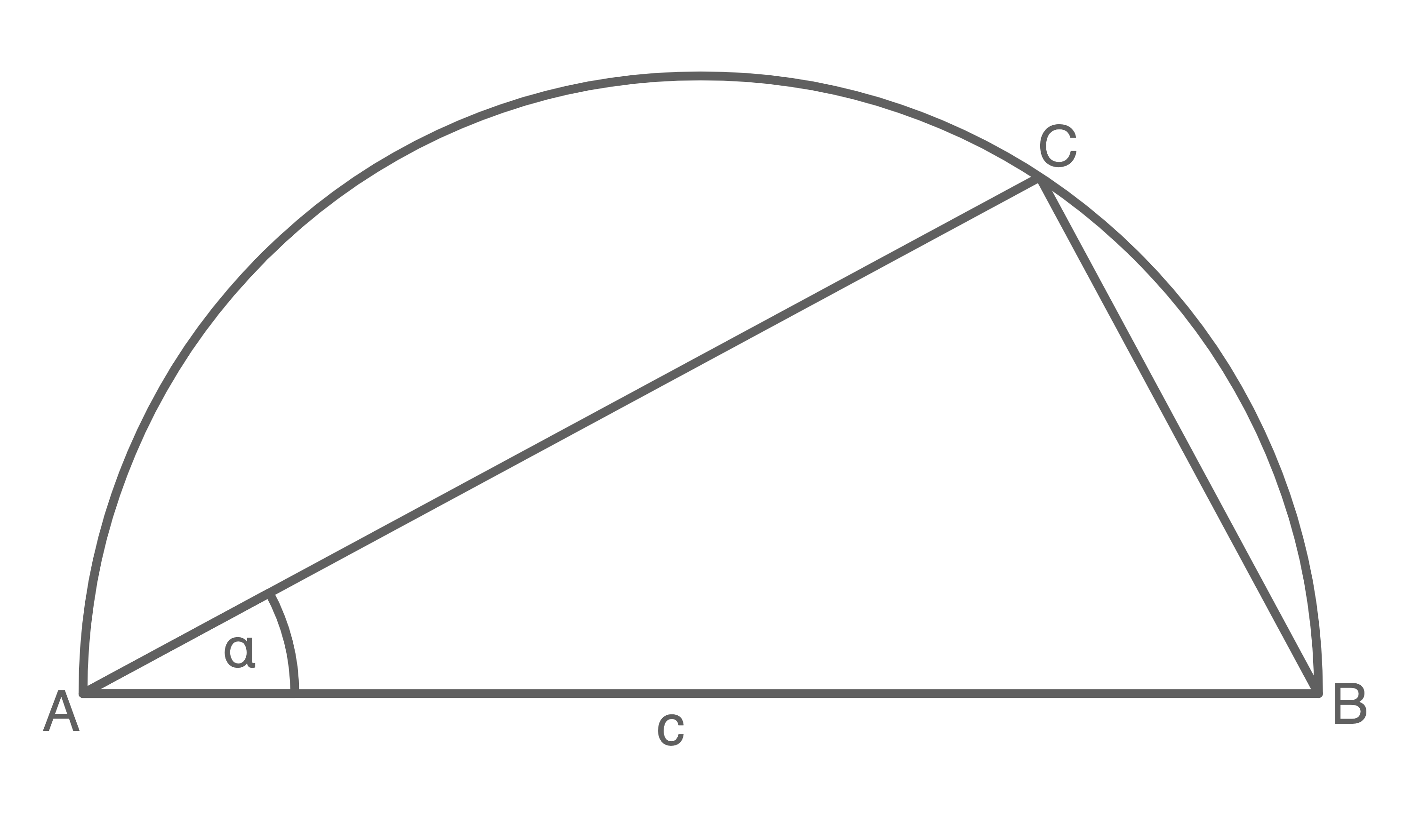
(Skizze nicht maßstabsgetreu)
(1 Pkt.)
7.
Am 1. Januar 2015 waren 
Menschen aus Baden-Württemberg Mitglied in einem Sportverein. Am 1. Januar 2018 waren es 
Menschen.
Berechne das durchschnittliche prozentuale Wachstum pro Jahr.
(1 Pkt.)
8.
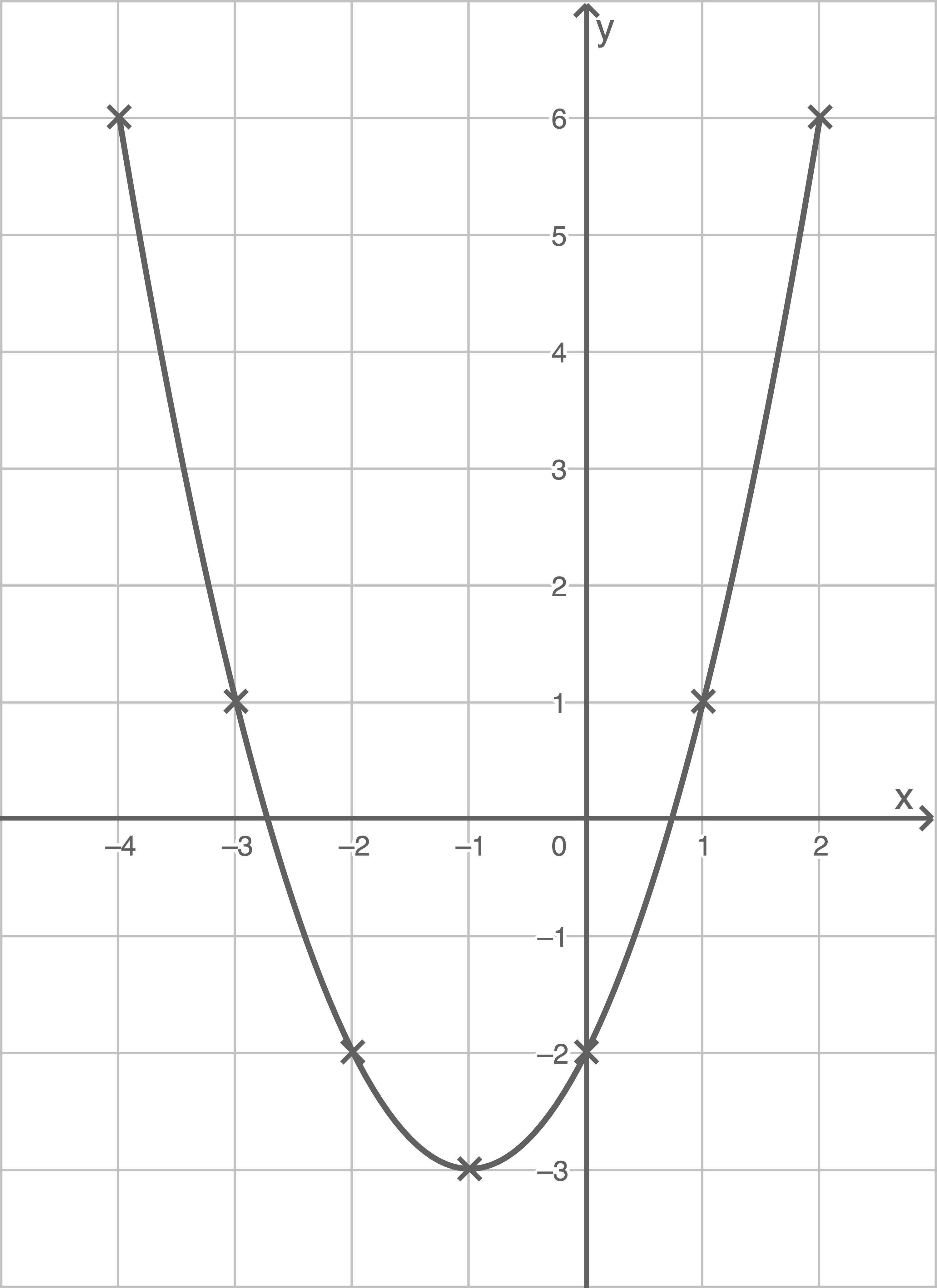
Die Parabel 
(siehe Abbildung) wird um 
Einheiten nach rechts verschoben.
Bestimme die neue Funktionsgleichung.
(1 Pkt.)
9.
In einer Fernsehspielshow werden die Mitspielerinnen bzw. die Mitspieler per Zufallsgenerator ausgewählt. Im Studio sitzen 
Männer und 
Frauen.
Bestimme die Wahrscheinlichkeit, dass 
Frauen ausgewählt werden.
(1 Pkt.)
10.
Fahrerweltmeisterschaft der Formel 1 - Bestimme das Diagramm zu dem beide Aussagen passen:
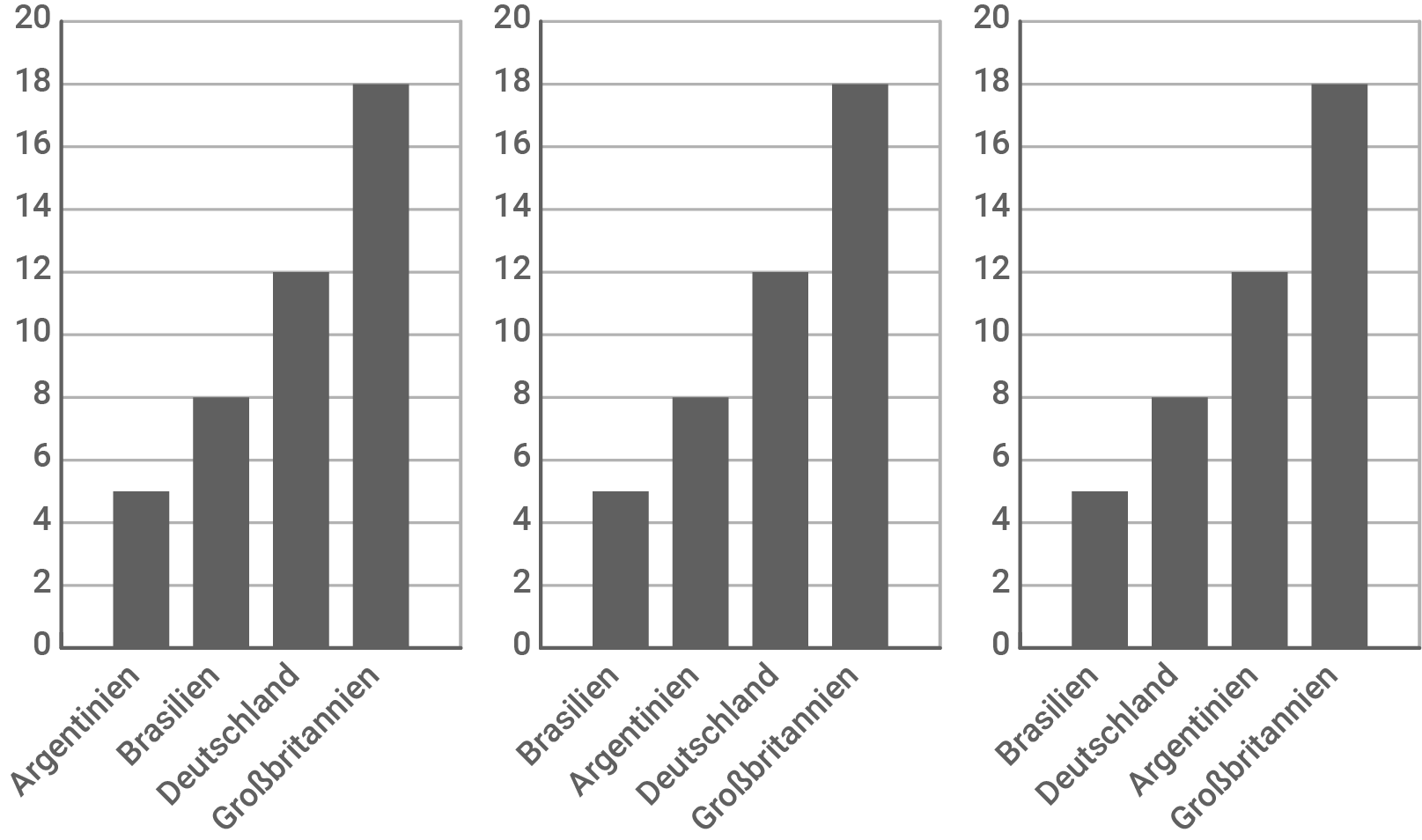
- Die Fahrer aus Deutschland gewannen nach den Fahrern aus Großbritannien die meisten Weltmeisterschaften.
- Die Fahrer aus Deutschland gewannen mehr als doppelt so viele Weltmeisterschaften wie die Fahrer aus Argentinien.
Diagramm A (links), Diagramm B (Mitte), Diagramm C (rechts)
(1 Pkt.)
1.
2.
Länge von 
berechnen
Dafür wird der 1. Strahlensatz angewendet:
![\(\begin{array}[t]{rll}
\dfrac{\overline{AB}}{\overline{BC}}&=&\dfrac{\overline{AE}}{\overline{DE}} &\quad \scriptsize \mid\;\cdot \overline{DE} \\[5pt]
\dfrac{\overline{AB}}{\overline{BC}}\cdot \overline{DE}&=&\overline{AE}&\\[5pt]
\overline{AE}&=&\dfrac{\overline{AB}}{\overline{BC}}\cdot \overline{DE}&\\[5pt]
\overline{AE}&=&\dfrac{1,9\,\text{m}}{7,6\,\text{m}}\cdot 10,5\,\text{m}&\\[5pt]
\overline{AE}&=&2,625\,\text{m}
\end{array}\)](https://mathjax.schullv.de/49522d615723cc776bee4141ebdeed590ab14ebf7d64598e1549e645153a6778?color=5a5a5a)
Länge von 
berechnen
![\(\begin{array}[t]{rll}
\overline{AD}&=&\overline{AE}+\overline{DE} \\[5pt]
\overline{AD}&=&2,625\,\text{m}+10,5\,\text{m} \\[5pt]
\overline{AD}&=&\boldsymbol{13,125\,\text{m}}
\end{array}\)](https://mathjax.schullv.de/41d4202a34c4535dbbe10fa41306b4382da3fb31d40549c3831f56639bdc5d26?color=5a5a5a)
3.
Volumen der Kugel:
![\(\begin{array}[t]{rll}
V&=& \dfrac{4}{3}\cdot \pi\cdot r^3& \\[5pt]
V&=& \dfrac{4}{3}\cdot \pi\cdot (12\,\text{cm})^3& \\[5pt]
V&\approx& 7\,238,23\,\text{cm}^3& \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a9afc5f1f9bb375b803b3a11582b71541ae618e5552aaa8685f327d131b49bca?color=5a5a5a)
Wenn das Kugelvolumen das Dreifache des Kegelvolumens wäre, müsste die Kugel allerdings ein Volumen von 
haben.
Somit ist die Behauptung falsch.
4.
(D) 
5.
Lösung über das Einsetzungsverfahren
Gleichung 
nach 
auflösen
![\(\begin{array}[t]{rll}
\text{(I)}&x-11&=&y &\quad \scriptsize \mid\;+11 \\[5pt]
\text{(I](https://mathjax.schullv.de/6b53a2959a3d0c85710103dea4b2df1eb69cdb03ba87176a43cb9e1b60d4b12c?color=5a5a5a)
Gleichung 
in Gleichung 
einsetzen
![\(\begin{array}[t]{rll}
2y+2x&=&10 \\[5pt]
2y+2\cdot (y+11)&=&10 &\\[5pt]
2y+2y+22&=&10 & \\[5pt]
4y+22&=&10 &\quad \scriptsize \mid\;-22 \\[5pt]
4y&=&-12 &\quad \scriptsize \mid\;:4 \\[5pt]
\boldsymbol{y}&=&\boldsymbol{-3}
\end{array}\)](https://mathjax.schullv.de/5b106ca0cbc21126363b2dc4f067e190d5425975fb251df95bbf2540e2d5cc16?color=5a5a5a)
in Gleichung einsetzen
![\(\begin{array}[t]{rll}
x&=&y+11 \\[5pt]
x&=&-3+11 \\[5pt]
\boldsymbol{x}&=&\boldsymbol{8}
\end{array}\)](https://mathjax.schullv.de/4f65a397b1f9f294b162f91d652028892c53821ae987761cd02f256da6e23479?color=5a5a5a)
6.
Laut dem Satz des Thales gilt: Das Dreieck hat bei Punkt 
einen rechten Winkel.
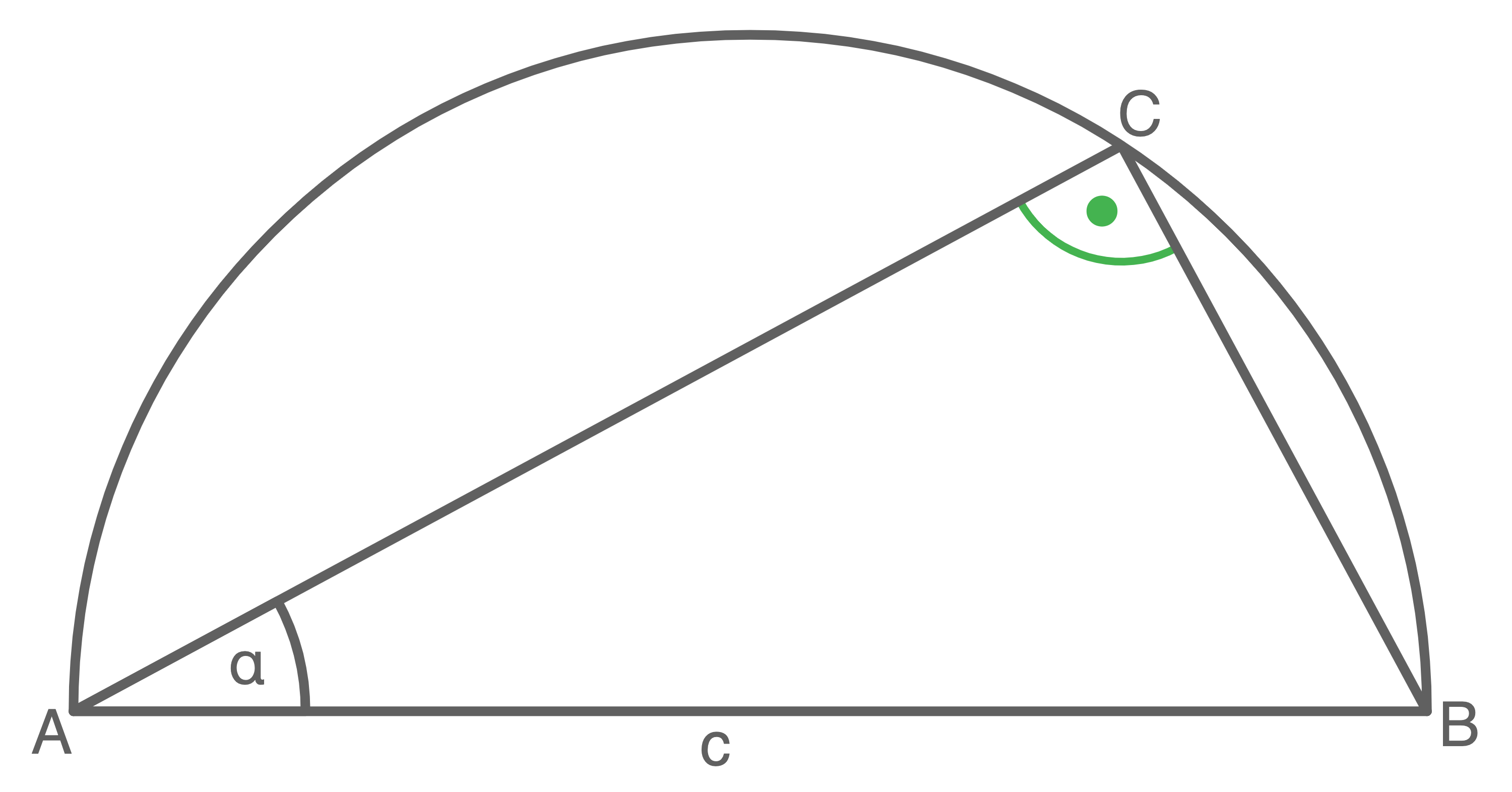Daraus folgt:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=&\dfrac{\overline{BC}}{c} &\quad \scriptsize \mid\;\cdot c \\[5pt]
\sin(\alpha)\cdot c&=&\overline{BC}&\\[5pt]
\overline{BC}&=&\sin(\alpha)\cdot c&\\[5pt]
\overline{BC}&=&\sin(53^{\circ})\cdot 8,8\,\text{cm}&\\[5pt]
\overline{BC}&\approx&\boldsymbol{7,03\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/71e8b1cc710a809afcab6e22af357f93b99a91da106f32b4d124d99a7f9e0bfd?color=5a5a5a)
7.
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot q^n \\[5pt]
W_3&=&W_0\cdot q^3 &\quad \scriptsize \mid\;:W_0 \\[5pt]
\dfrac{W_3}{W_0}&=&q^3 & \\[5pt]
q^3&=&\dfrac{W_3}{W_0}&\quad \scriptsize \mid\;\sqrt[3]{\,\,}\\[5pt]
q&=&\sqrt[3]{\dfrac{W_3}{W_0}} & \\[5pt]
q&=&\sqrt[3]{\dfrac{3\,760\,912}{3\,703\,759}} & \\[5pt]
q&\approx&1,005
\end{array}\)](https://mathjax.schullv.de/cfe767604a784acbe6fa5fd6945bc41ba7a1c343cab8086d7af87d39d597c95d?color=5a5a5a)
Menschen
Jahre
Menschen
8.
9.
Insgesamt gibt es 
Mitspieler*innen.
Somit gilt:
![\(\begin{array}[t]{rll}
P(\text{zwei Frauen})&=&\dfrac{43}{75}\cdot\dfrac{42}{74} \\[5pt]
&=&\boldsymbol{\dfrac{301}{925}}\\[5pt]
&\approx&0,325=\boldsymbol{32,5\,\%}
\end{array}\)](https://mathjax.schullv.de/b670d84a7487dbfb7c108a338e6bdd9becf373053c98c2645c8519e708cddbd7?color=5a5a5a)
10.
Diagramm A