Pflichtteil A2
1.
Lars macht einen Zufallsversuch mit drei roten, einer gelben und zwei schwarzen Kugeln.
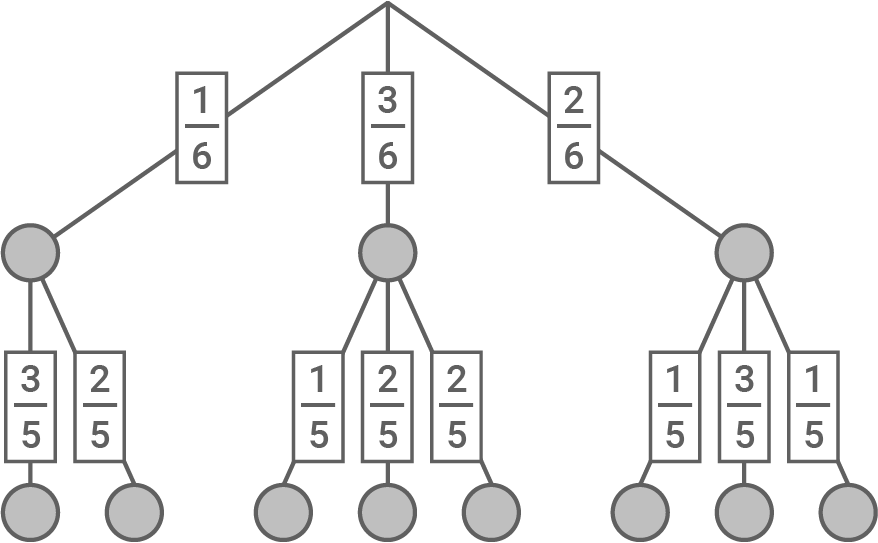

- Überprüfe die Aussagen und begründe.
A) Es handelt sich um einen Zufallsversuch mit Zurücklegen.
B) Wahrscheinlichkeit:

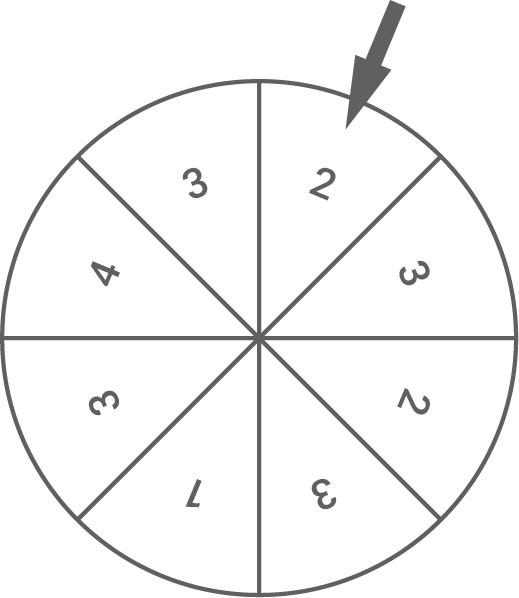
- Berechne die Wahrscheinlichkeit, bei zweimaligem Drehen eine Summe von höchstens
zu erhalten. (Summe
)
(3 Pkt.)
2.
Der Flächeninhalt der zusammengesetzten Figur beträgt  .
.
Die Seite ist
ist  länger als die Seite
länger als die Seite 
Die Höhe beträgt
beträgt  .
.
Die Seite
Die Höhe
- Berechne
und
stelle dazu zunächst eine Gleichung auf.
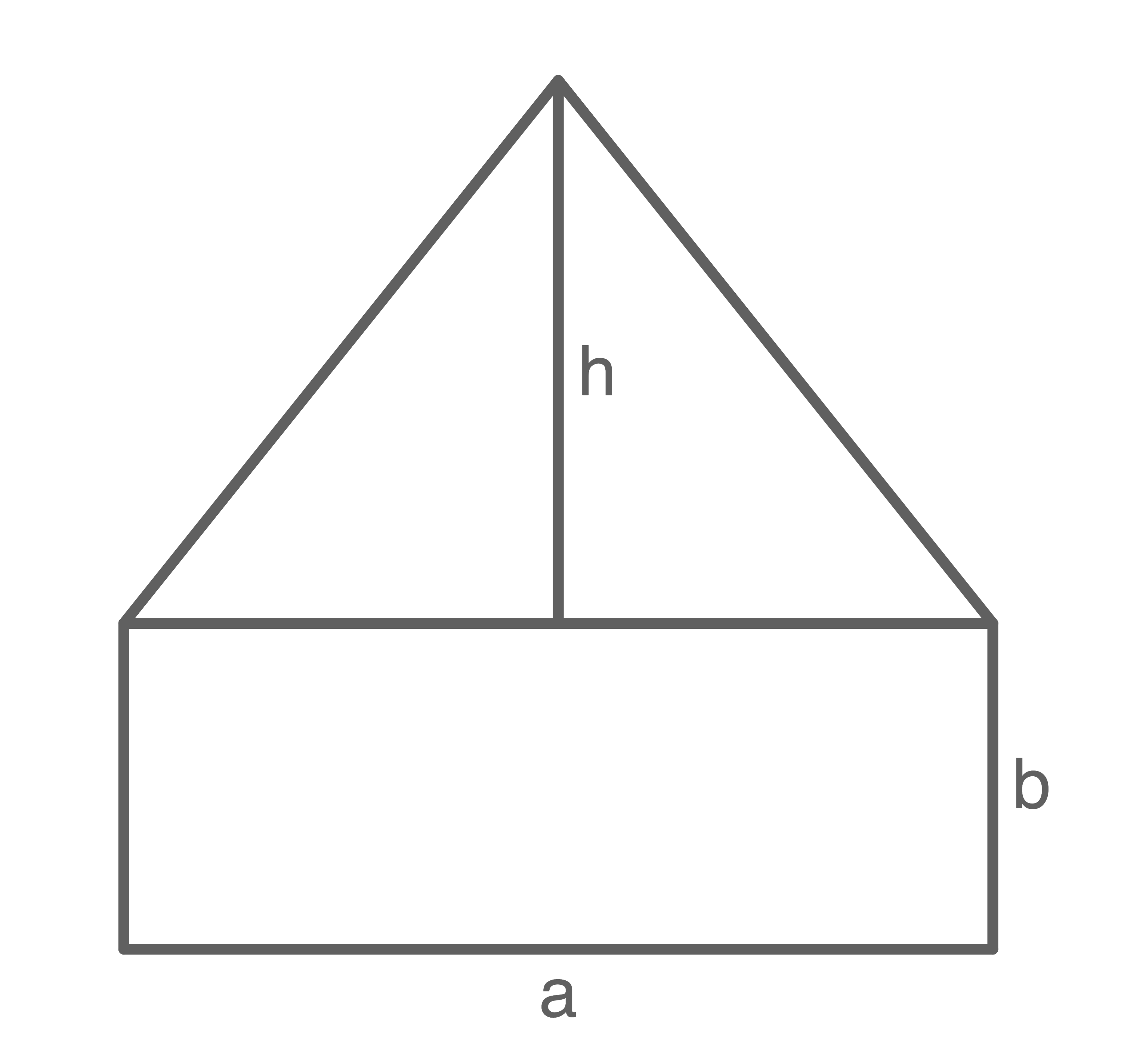
(Abbildung nicht maßstabsgetreu)
(2 Pkt.)
3.
Beim Stern von Bethlehem handelt es sich um eine Sternenkonstellation, bei der sich die Planeten Saturn und Jupiter auf ihren Umlaufbahnen nahe kommen.
Von der Erde aus kann man dann ihren Abstand kaum noch wahrnehmen. Am 21.12.2020 lagen die beiden Planeten von der Erde aus gesehen nur auseinander.
auseinander.
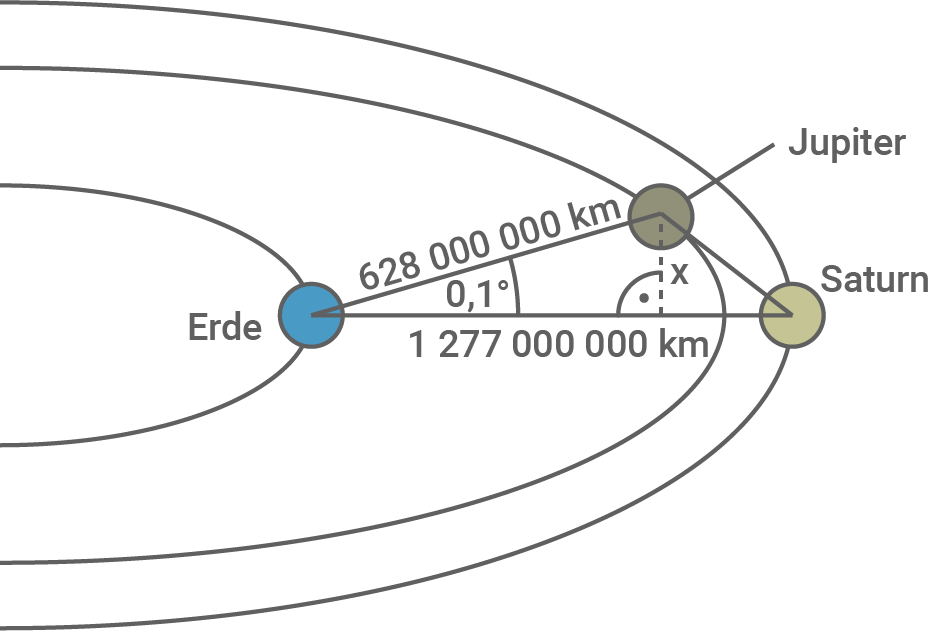
Von der Erde aus kann man dann ihren Abstand kaum noch wahrnehmen. Am 21.12.2020 lagen die beiden Planeten von der Erde aus gesehen nur

(Abbildung nicht maßstabsgetreu)
- Berechne
in
.
- Berechne die in der Tabelle fehlenden Werte.
(3 Pkt.)
4.
Für die Skizze gilt:  und
und  .
.
 wird ein Quadrat eingezeichnet.
wird ein Quadrat eingezeichnet.
Die vier Eckpunkte liegen auf der Kreislinie.
- Berechne
Die vier Eckpunkte liegen auf der Kreislinie.
- Erstelle eine Skizze und berechne den Flächeninhalt des Quadrates.
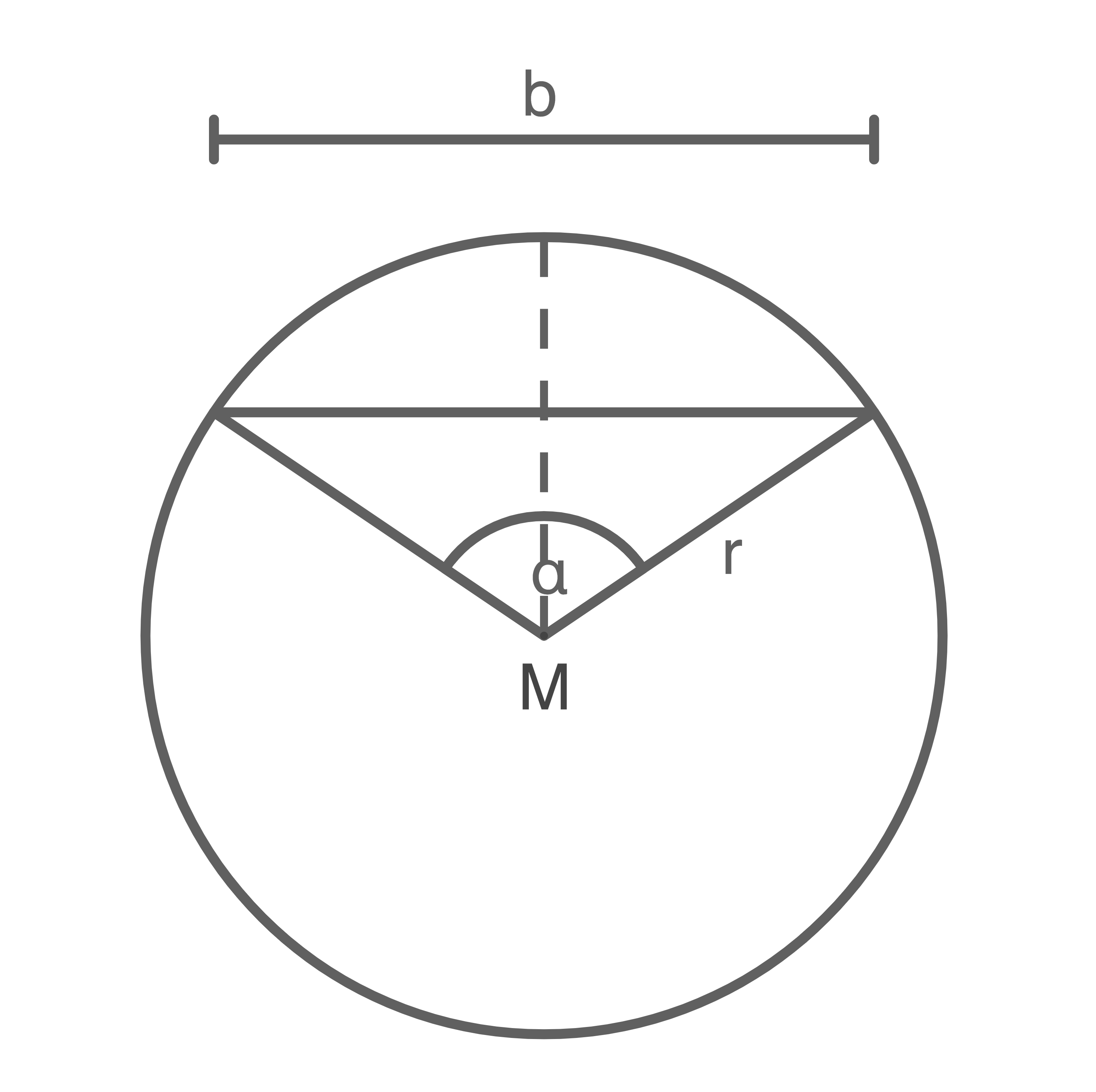
(Abbildung nicht maßstabsgetreu)
(3 Pkt.)
5.
Vor drei Jahren hat Familie Kramer bei einer Bank  angelegt:
angelegt:
- Berechne, welcher Betrag Familie Kramer nach Ablauf der drei Jahre zur Verfügung steht.
| Laufzeit: | |
| Zinssatz: | |
| (Zinsen werden mitverzinst) | |
Dieses Geld wurde ausbezahlt. Davon werden  zum Kauf eines neuen Autos (Gesamtpreis
zum Kauf eines neuen Autos (Gesamtpreis  ) als Anzahlung verwendet.
) als Anzahlung verwendet.
Der Rest muss über eine Bank in Form eines Annuitätendarlehens finanziert werden:
Der Rest muss über eine Bank in Form eines Annuitätendarlehens finanziert werden:
| Zinssatz: | |
| Laufzeit: | |
| Monatliche Rate: |
- Berechne die Tilgung der ersten beiden Monate.
Kredithöhe
MonatsanfangZinsen Rate Tilgung Kredithöhe
Monatsende
(2 Pkt.)
6.
Ein Wasserspeicher hat die Form eines Zylinders mit aufgesetztem Kegel (siehe Abbildung).
In das zylinderförmige Wasserbecken passen, vollständig gefüllt, Wasser.
Wasser.
Folgende weitere Maße sind bekannt:

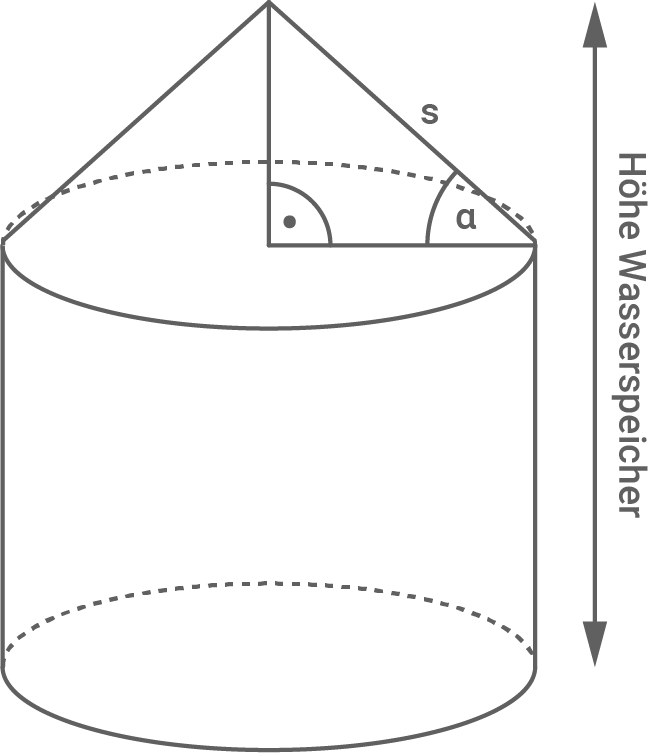
In das zylinderförmige Wasserbecken passen, vollständig gefüllt,
Folgende weitere Maße sind bekannt:

(Abbildung nicht maßstabsgetreu)
- Berechne die Höhe des Wasserbeckens.
- Berechne die Gesamthöhe des Wasserspeichers.
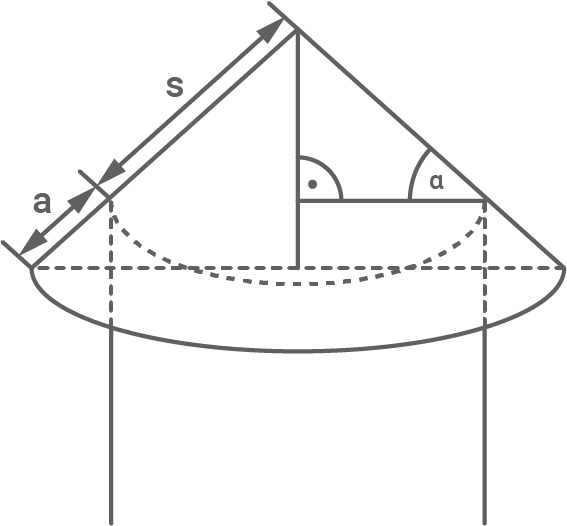
Das Blechdach des Wasserspeichers soll ersetzt werden. Der Dachüberstand beträgt  (siehe Abbildung).
(siehe Abbildung).

(Abbildung nicht maßstabsgetreu)
- Berechne, wie viel
Blech benötigt werden.
(3 Pkt.)
7.
Die Parabel  wird an der
wird an der  -Achse gespiegelt.
-Achse gespiegelt.
Der Scheitelpunkt wird um nach oben verschoben.
nach oben verschoben.
Der Scheitelpunkt wird um
- Nenne die Funktionsgleichung für die neue Parabel.
- Zeichne die Parabel
in ein geeignetes Koordinatensystem ein.
(2 Pkt.)
8.
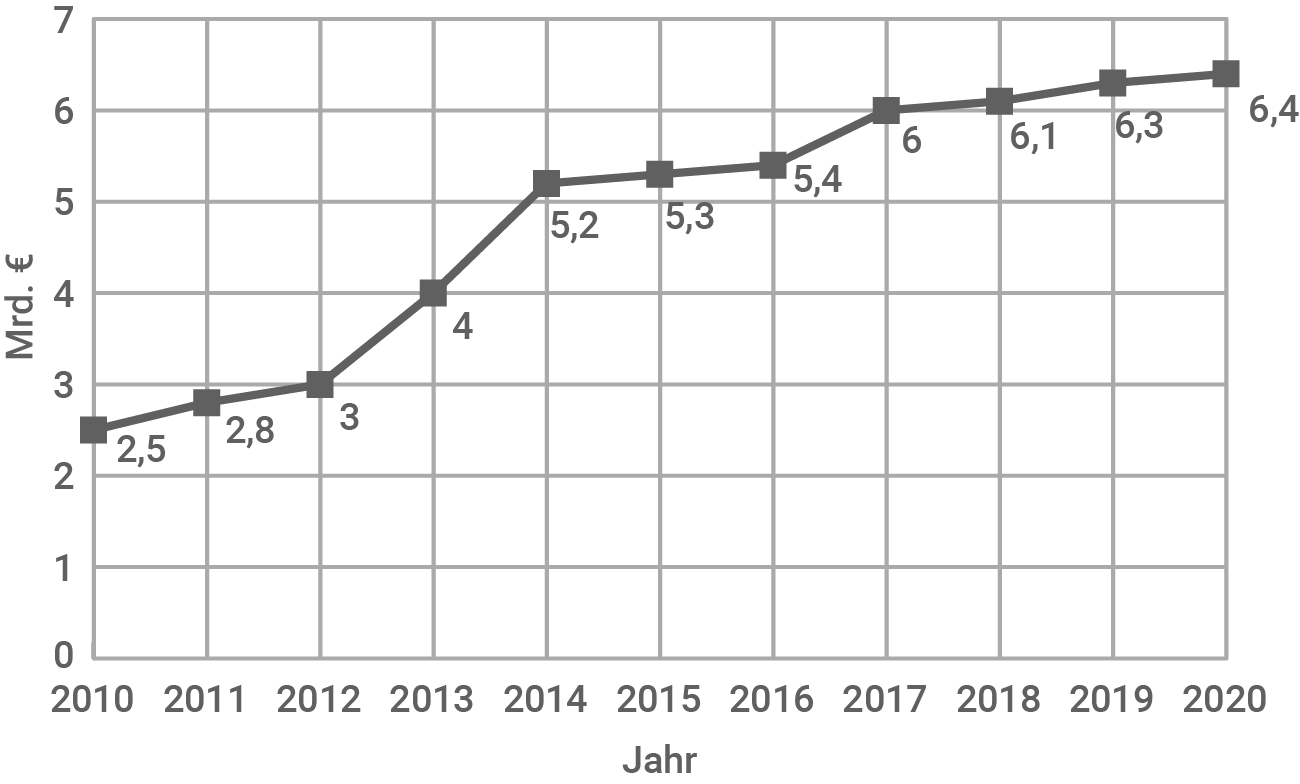
Die Grafik zeigt die Kostenentwicklung beim Bau eines Großflughafens.
 Die durchschnittliche jährliche Kostensteigerung von
Die durchschnittliche jährliche Kostensteigerung von  bis
bis  betrug
betrug 
- Berechne, um wie viel Prozent die Kosten von
bis
angestiegen sind.
- Bestimme, in welchen beiden aufeinanderfolgenden Jahren der Kostenanstieg prozentual am größten war.

Kostenentwicklung beim Bau eines Großflughafens
- Berechne, auf welchen Betrag eine Geldanlage von
mit diesem jährlichen Zinssatz von
bis
angestiegen wäre.
(Die Zinsen werden mitverzinst.)
(2 Pkt.)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Aussagen überprüfen und begründen
Aussage A) ist falsch.
Zunächst wird aus sechs Kugeln gezogen und anschließend aus fünf Kugeln. Der Nenner verändert sich von auf
auf  und deshalb wird die gezogene Kugel also nicht zurückgelegt.
Aussage B) ist richtig.
und deshalb wird die gezogene Kugel also nicht zurückgelegt.
Aussage B) ist richtig.
 Wahrscheinlichkeit für Summe berechnen
Mögliche Ergebnisse für Summe höchstens 4:
Wahrscheinlichkeit für Summe berechnen
Mögliche Ergebnisse für Summe höchstens 4:




 Um beim zweimaligen Drehen eine Summe von höchstens 4 zu erhalten, beträgt die Wahrscheinlichkeit
Um beim zweimaligen Drehen eine Summe von höchstens 4 zu erhalten, beträgt die Wahrscheinlichkeit 
Zunächst wird aus sechs Kugeln gezogen und anschließend aus fünf Kugeln. Der Nenner verändert sich von
2.
Für den gesamten Flächeninhalt gilt:  In Abhängkeit von
In Abhängkeit von  und
und  bedeutet das:
bedeutet das:
 Es gilt
Es gilt  und
und  also folgt:
also folgt:
 Der Flächeninhalt beträgt
Der Flächeninhalt beträgt  die Formel wird also mit
die Formel wird also mit  gleichgesetzt:
gleichgesetzt:
![\(\begin{array}[t]{rll}
a\cdot (a-6)+\dfrac{1}{2}\cdot a\cdot 7&=&75 \\[5pt]
a^2-6a+3,5a&=&75 \\[5pt]
a^2-2,5a&=&75 & \scriptsize \mid\; -75\\[5pt]
a^2-2,5a-75&=&0\\[5pt]
\end{array}\)](https://mathjax.schullv.de/9dd5d13f68743cf5dfcfea59fa1f50c0b21d07a9c1e115b2cdc10e3436aefb37?color=5a5a5a)
![\(\begin{array}[t]{rll}
a_{1,2}&=& -\dfrac{p}{2} \pm \sqrt{\left(\dfrac{p}{2}\right)^2-q} \\[5pt]
&=& -\dfrac{-2,5}{2} \pm \sqrt{\left(\dfrac{-2,5}{2}\right)^2-(-75)} \\[5pt]
&=& 1,25 \pm \sqrt{\left(-1,25\right)^2+75} \\[5pt]
a_{1,2}&=& 1,25 \pm 8,75\\[5pt]
a_1&=&10\\[5pt]
a_2&=&-7,5
\end{array}\)](https://mathjax.schullv.de/845ac508360670fadf1b3e7e61077c07c95d3bf9477722c4e097a514db1ee98b?color=5a5a5a)
 ist die einzige Lösung, da
ist die einzige Lösung, da  keine Längenangabe ist (wegen negativem Vorzeichen)
Daraus folgt für
keine Längenangabe ist (wegen negativem Vorzeichen)
Daraus folgt für 
 Die Strecken sind also
Die Strecken sind also  und
und  lang.
lang.
3.
4.
Länge von  berechnen
Skizze erstellen und Flächeninhalt berechnen
berechnen
Skizze erstellen und Flächeninhalt berechnen
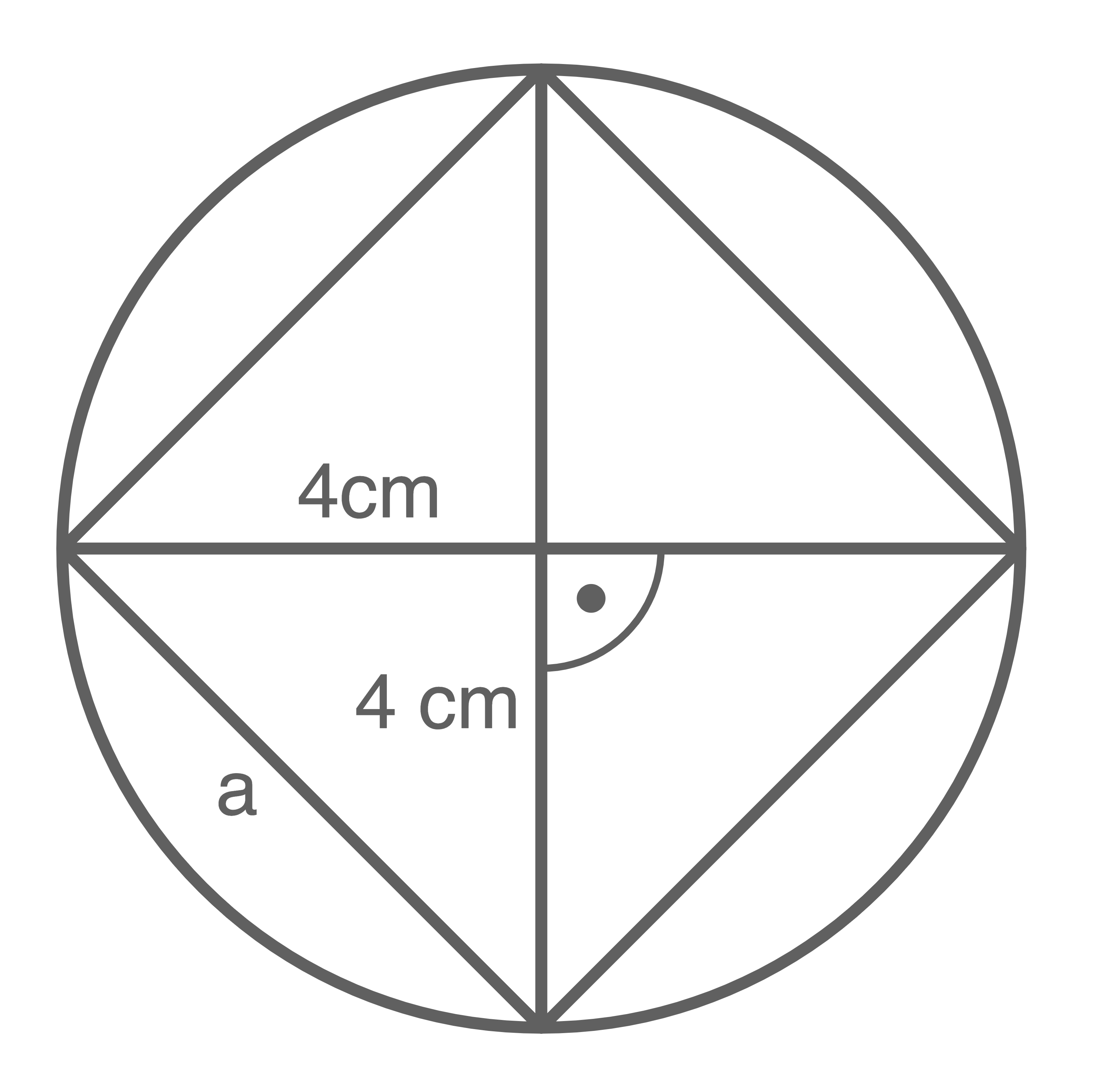 Der Flächeninhalt des Quadrats lässt sich berechnen über
Der Flächeninhalt des Quadrats lässt sich berechnen über  Mit dem Satz des Pythagoras lässt sich
Mit dem Satz des Pythagoras lässt sich  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
a^2&=&(4\,\text{cm})^2+(4\,\text{cm})^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
a&=&\sqrt{32\,\text{cm}^2}=\sqrt{32}\,\text{cm}
\end{array}\)](https://mathjax.schullv.de/87515a3eca6d9bfe3f4af5be2307dd3149107213962e4c300c9bae133a27c22a?color=5a5a5a)


5.
Betrag berechnen

 Nach Ablauf der drei Jahre, stehen Familie Kramer also
Nach Ablauf der drei Jahre, stehen Familie Kramer also  zur Verfügung.
Tilgung berechnen
zur Verfügung.
Tilgung berechnen
In den ersten beide Monaten werden also  und
und  getilgt.
getilgt.
| Kredithöhe Monatsanfang | ||
|---|---|---|
| Zinsen | ||
| Rate | ||
| Tilgung | ||
| Kredithöhe Monatsende |
6.
Höhe des Wasserbeckens berechnen
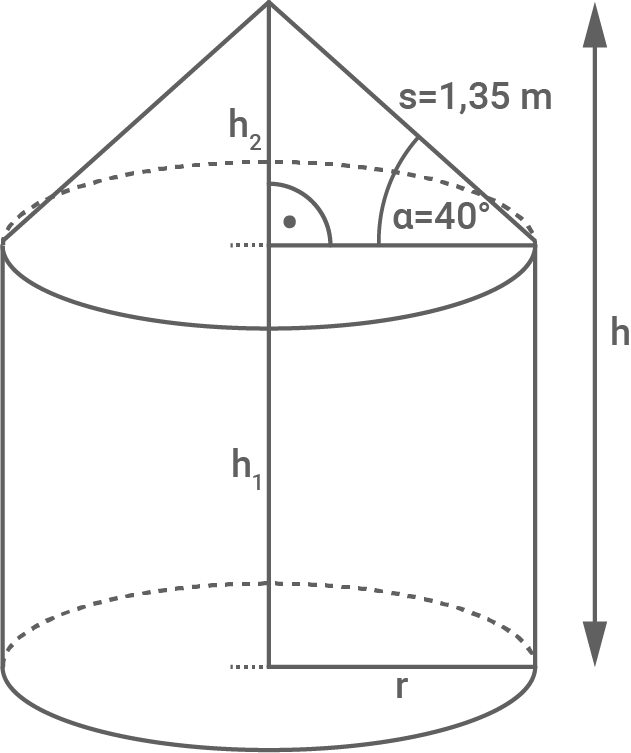 1. Schritt: Radius
1. Schritt: Radius  des Wasserbeckens berechnen
des Wasserbeckens berechnen
![\(\begin{array}[t]{rll}
\cos(40^\circ)&=&\dfrac{r}{1,35\,\text{m}} &\scriptsize \mid\;\cdot 1,35\,\text{m} \\[5pt]
r&=&\cos(40^\circ)\cdot 1,35\,\text{m}\\[5pt]
r&\approx& 1,03\,\text{m}
\end{array}\)](https://mathjax.schullv.de/54fdff84d60c311a92ba6cafb5c9ead9107b7d7fd438dc1111324b63dbb5b754?color=5a5a5a) 2. Schritt: Höhe
2. Schritt: Höhe  des Wasserbeckens berechnen
des Wasserbeckens berechnen


![\(\begin{array}[t]{rll}
\pi\cdot (1,03\,\text{m})^2\cdot h_1&=&8\,\text{m}^3 \quad \scriptsize \mid\;:(\pi\cdot (1,03\,\text{m})^2) \\[5pt]
h_1&=&\dfrac{8\,\text{m}^3}{\pi\cdot (1,03\,\text{m})^2}\\[5pt]
h_1&\approx&2,4\,\text{m}
\end{array}\)](https://mathjax.schullv.de/8f96670659b1ec3d3099211032542d480de784b0b179f1619ba6b3f1901ae828?color=5a5a5a) Das Wasserbecken ist also ca.
Das Wasserbecken ist also ca.  hoch.
Gesamthöhe des Wasserspeichers berechnen
1. Schritt: Höhe
hoch.
Gesamthöhe des Wasserspeichers berechnen
1. Schritt: Höhe  des Kegels berechnen
des Kegels berechnen
![\(\begin{array}[t]{rll}
\sin(40^\circ)&=&\dfrac{h_2}{1,35\,\text{m}} \quad \scriptsize \mid\;\cdot 1,35\,\text{m} \\[5pt]
\sin(40^\circ)\cdot 1,35\,\text{m} &=&h_2 \\[5pt]
h_2&\approx&0,87\,\text{m}
\end{array}\)](https://mathjax.schullv.de/cf61c3eb71560ced729def2660826f8e7bfdd9911c3e08476a1694bd583d4de4?color=5a5a5a) 2. Schritt: Gesamthöhe
2. Schritt: Gesamthöhe  berechnen
berechnen

 Der gesamte Wasserspeicher ist
Der gesamte Wasserspeicher ist  hoch.
Benötigte Fläche an Blech berechnen
hoch.
Benötigte Fläche an Blech berechnen
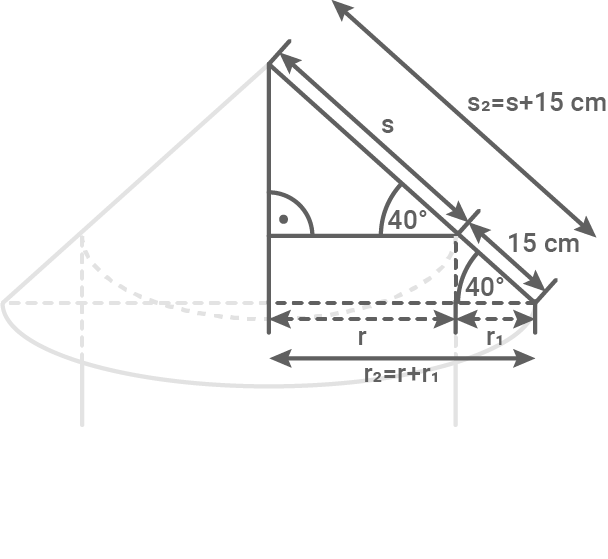 Das Blechdach stellt eine Mantelfläche (
Das Blechdach stellt eine Mantelfläche ( ) eines Kegels dar.
1. Schritt: Streckenlängen von
) eines Kegels dar.
1. Schritt: Streckenlängen von  und
und  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(40^\circ)&=&\dfrac{r_1}{0,15\,\text{m}} \quad \scriptsize \mid\; \cdot 0,15\,\text{m}\\[5pt]
r_1&=&\cos(40^\circ)\cdot 0,15\,\text{m}\\[5pt]
r_1&\approx&0,11\,\text{m}
\end{array}\)](https://mathjax.schullv.de/ec1bb434568f829c5633df5cbc088d860b6460c952111908e8a2f5b9d6f9f115?color=5a5a5a)
 2. Schritt: Blechbedarf berechnen
2. Schritt: Blechbedarf berechnen



![\(\begin{array}[t]{rll}
M&=&\pi\cdot r_2\cdot s_2 \\[5pt]
&=&\pi\cdot 1,14\,\text{m} \cdot 1,5\,\text{m}\\[5pt]
M&\approx&5,37\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/6ea09b533dbbd1743af371f787a094a58fb624bcc1f1411c9f49d88b715aa387?color=5a5a5a) Es werden also ca.
Es werden also ca.  Blech benötigt.
Blech benötigt.


7.
Funktionsgleichung nennen
Zunächst wird die Parabel an der  -Achse gespiegelt und hat dann die Funktionsgleichung
-Achse gespiegelt und hat dann die Funktionsgleichung  Anschließend wird diese um
Anschließend wird diese um  nach oben verschoben. Die gesuchte Funktionsgleichung lautet damit:
nach oben verschoben. Die gesuchte Funktionsgleichung lautet damit:  Parabel zeichnen
Parabel zeichnen
 Wertetabelle
Wertetabelle
Schaubild
Aufgrund der Achsensymmetrie zur  -Achse gelten für die
-Achse gelten für die  -Werte
-Werte  und
und  die gleichen
die gleichen  -Werte wie für
-Werte wie für  und
und 
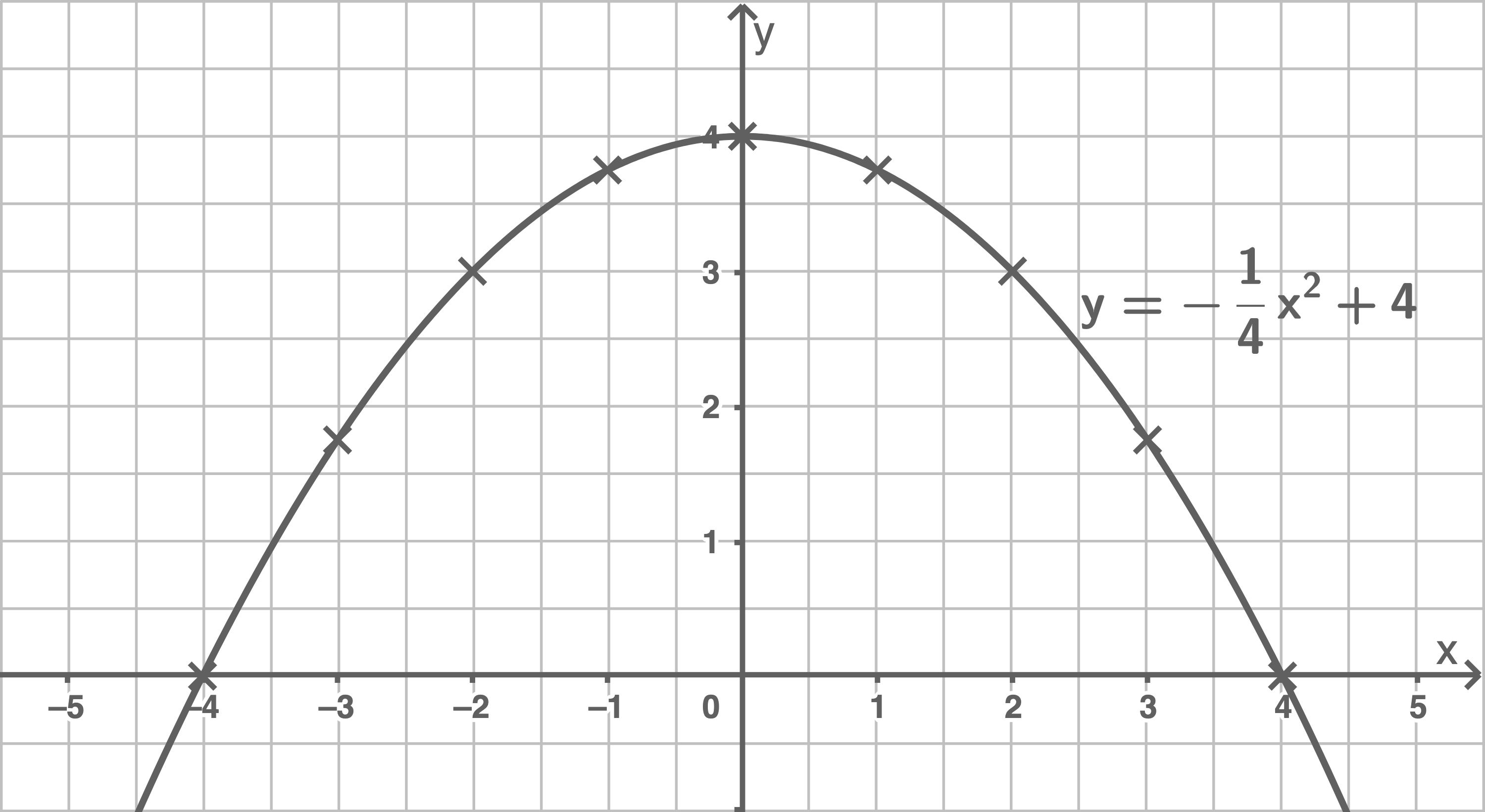

8.
Anstieg berechnen



 Prozentualer Anstieg:
Prozentualer Anstieg:
 Die Kosten sind also um
Die Kosten sind also um  gestiegen.
Größten Kostenanstieg bestimmen
Am Schaubild lässt sich ablesen, dass der steilste Anstieg in den Jahren
gestiegen.
Größten Kostenanstieg bestimmen
Am Schaubild lässt sich ablesen, dass der steilste Anstieg in den Jahren  (von
(von  bis
bis  ) und
) und  (von
(von  bis
bis  ) war.
Betrag berechnen
) war.
Betrag berechnen

 Nach zehn Jahren wäre die Geldanlage auf
Nach zehn Jahren wäre die Geldanlage auf  angestiegen.
angestiegen.
