Pflichtteil A1
1.
Löse das Gleichungssystem.

(1 Pkt.)
2.
Vervollständige die Formeln.


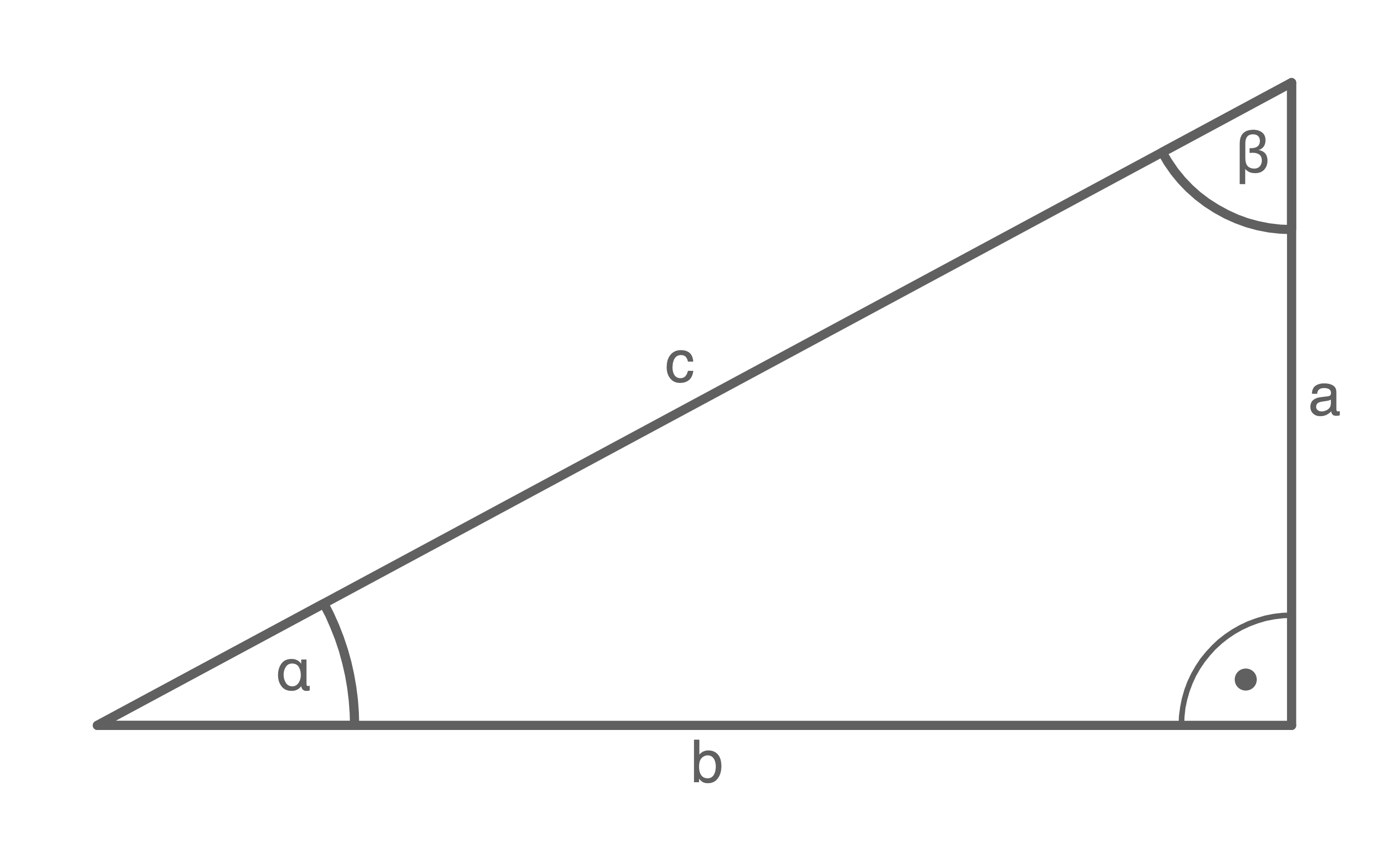
(1 Pkt.)
3.
Eine Parabel  mit der Funktionsgleichung
mit der Funktionsgleichung  wird an der Geraden
wird an der Geraden  gespiegelt.
gespiegelt.
Kreuze die Funktionsgleichung der gespiegelten Parabel an.
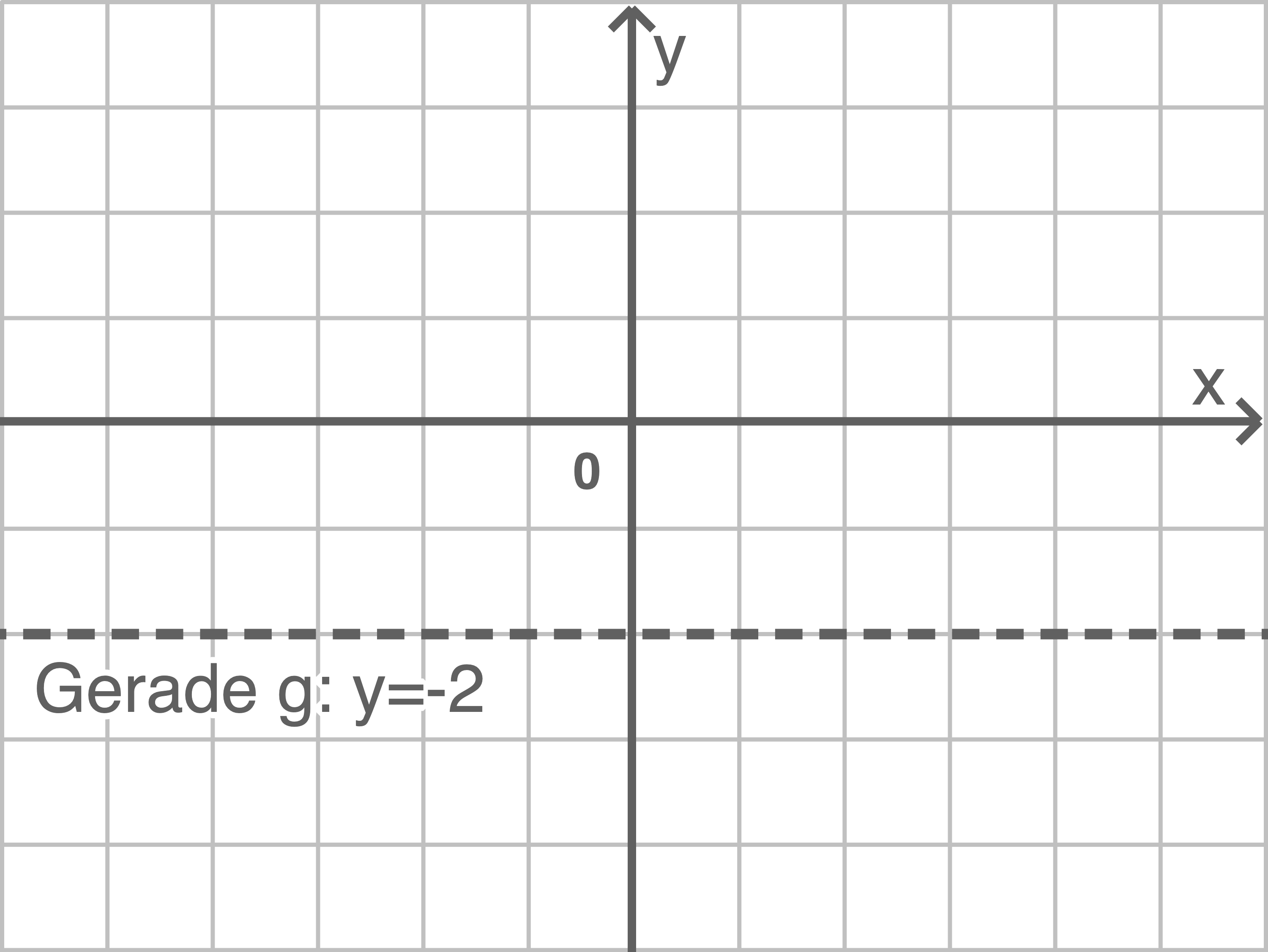
Kreuze die Funktionsgleichung der gespiegelten Parabel an.

(1 Pkt.)
4.
Welches dieser Dreiecke hat einen rechten Winkel? Begründe.
A) 
 und
und 
B)
 und
und 
C)
 und
und 
D)
 und
und 
B)
C)
D)
(1 Pkt.)
5.
In einer Messstation zwischen Russland und Alaska wurden von Juli bis Dezember folgende monatliche Durchschnittstemperaturen gemessen.
| Monat | Durchschnittstemperaturen |
|---|---|
| Jul | |
| Aug | |
| Sep | |
| Okt | |
| Nov | |
| Dez |
- Gib den Mittelwert der Messwerte von Juli bis Dezember an.
- Bestimme den Temperaturunterschied zwischen Juli und Dezember.
(1 Pkt.)
6.
Jano behauptet: „Die Gleichung  hat zwei Lösungen.“
Stimmt die Aussage? Begründe.
hat zwei Lösungen.“
Stimmt die Aussage? Begründe.
(1 Pkt.)
7.
Bestimme den Winkel  ohne zu messen.
ohne zu messen.
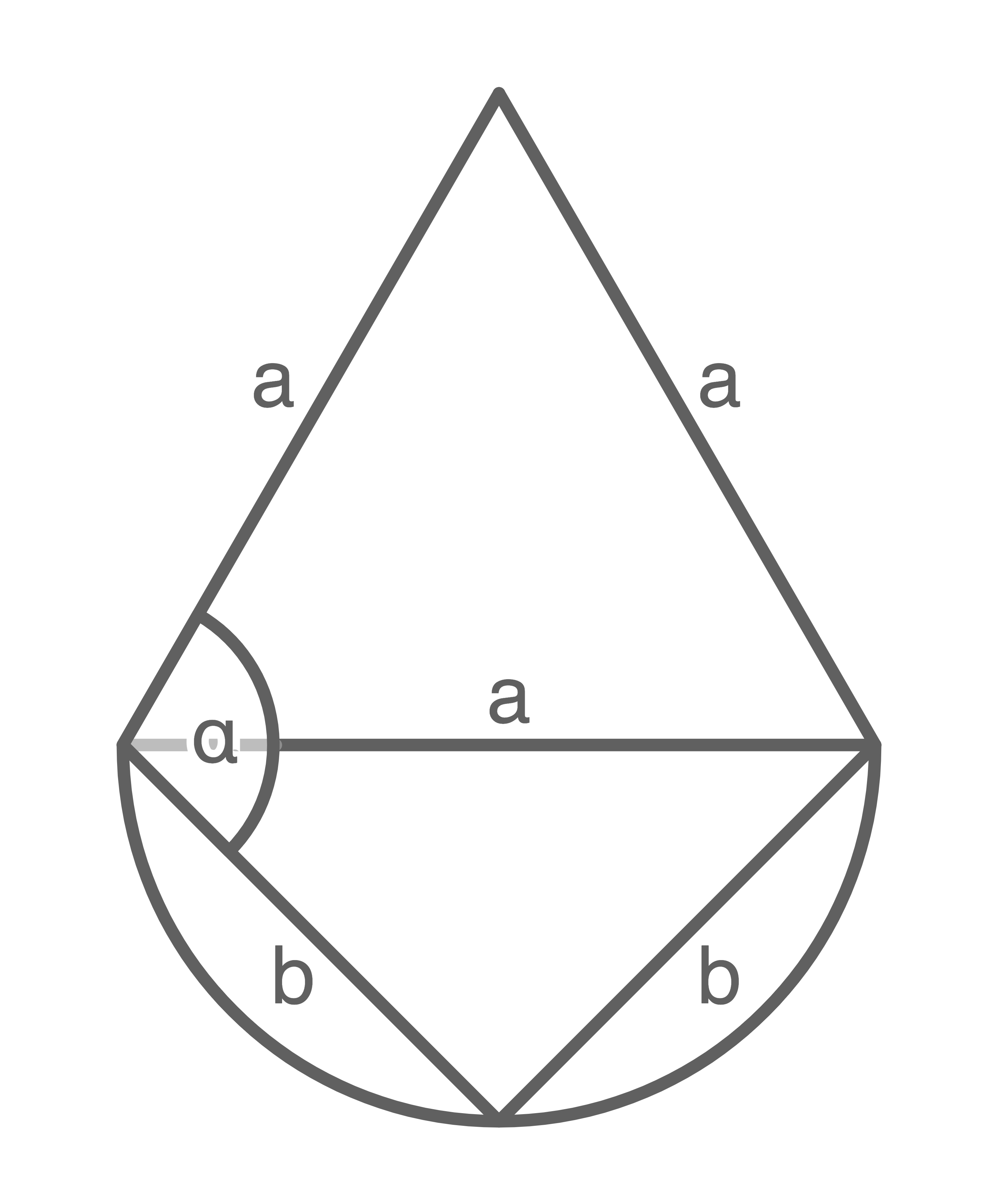

(Abbildung nicht maßstabsgetreu)
(1 Pkt.)
8.
Vervollständige den Streckenzug im Würfelnetz.
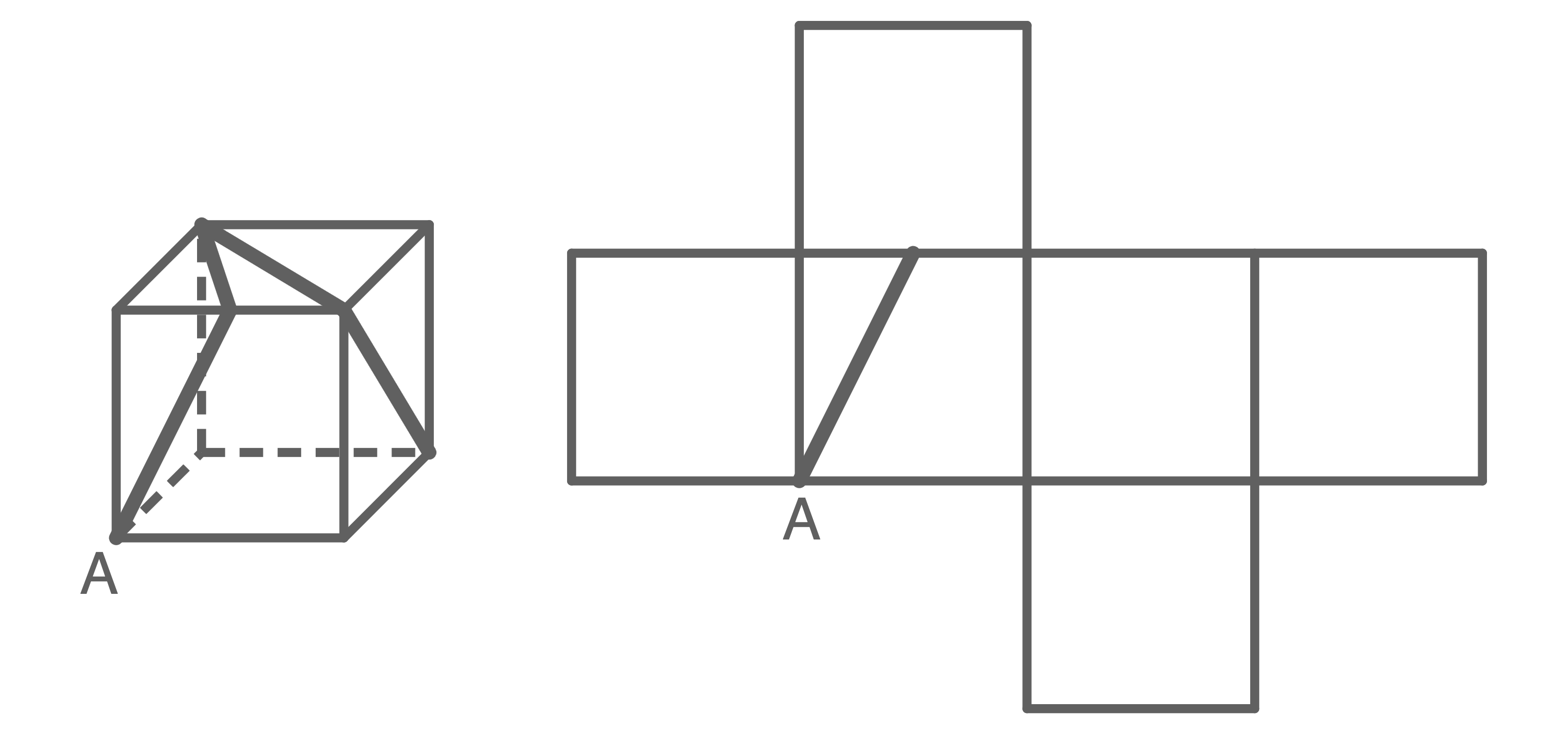

(1 Pkt.)
9.
Berechne die Höhe des Hauses.
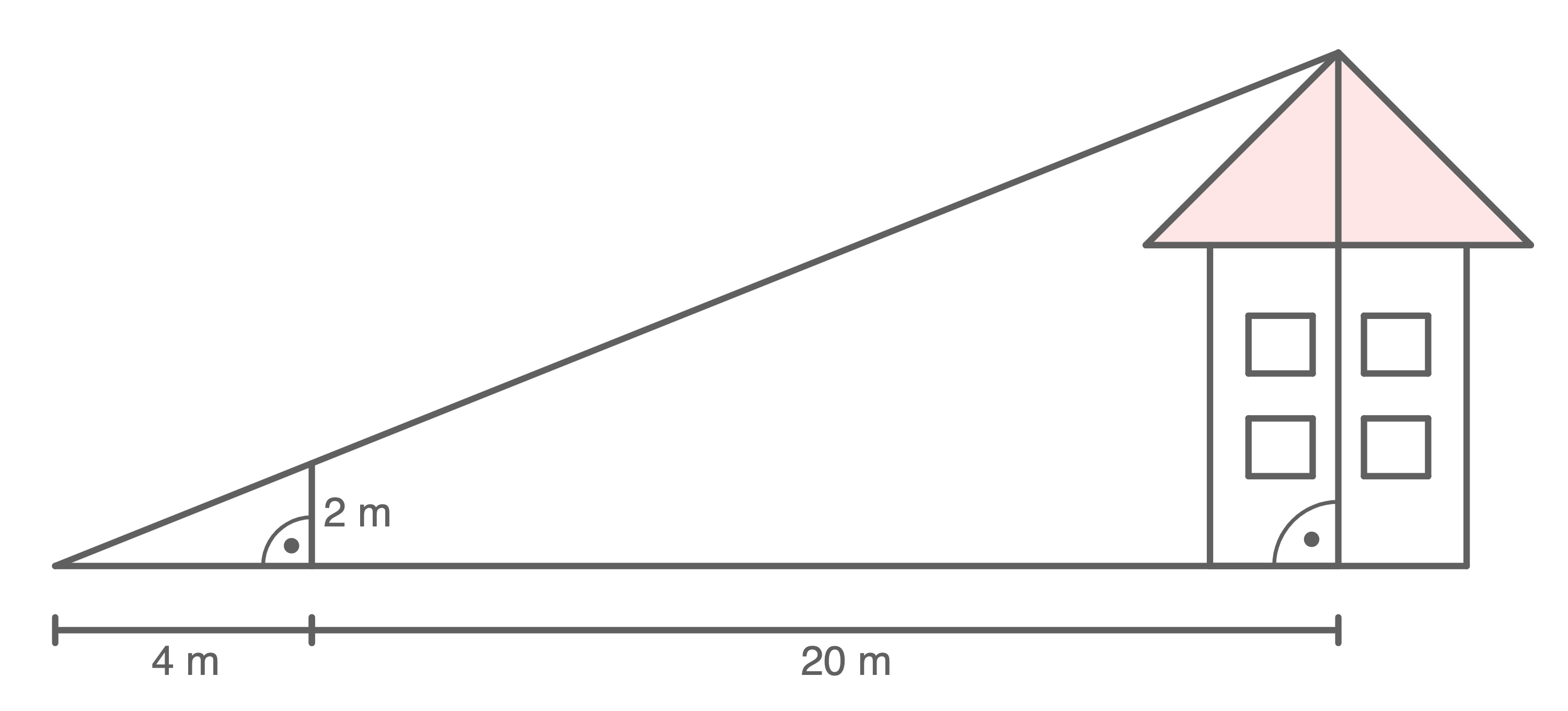

(Abbildung nicht maßstabsgetreu)
(1 Pkt.)
10.
Beim Memory-Spiel sind immer zwei Karten mit demselben Bild enthalten.
 Der Spieler, der an der Reihe ist, darf zwei Karten umdrehen.
Der Spieler, der an der Reihe ist, darf zwei Karten umdrehen.
Jan hat die oberen Paare bereits gefunden, es sind nur noch die Karten rechts unten im Spiel.
Er ist wieder an der Reihe und hat schon eine Karte mit einer Sonne umgedreht.


Jan hat die oberen Paare bereits gefunden, es sind nur noch die Karten rechts unten im Spiel.
Er ist wieder an der Reihe und hat schon eine Karte mit einer Sonne umgedreht.
- Berechne die Wahrscheinlichkeit, dass auf der zweiten Karte eine Sonne ist.

(1 Pkt.)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
Lösungsmöglichkeit A
(Gleichsetzungsverfahren) Beide Gleichungen werden nach
Beide Gleichungen werden nach  aufgelöst:
aufgelöst:


![\(\begin{array}{rll}
3,5y-12&=&32-2y&\scriptsize\mid\; +2y\\[5pt]
5,5y-12&=&32&\scriptsize\mid\; +12\\[5pt]
5,5y&=&44&\scriptsize\mid\; :5,5\\[5pt]
y&=&8
\end{array}\)](https://mathjax.schullv.de/e3b2acbabcd881bdc2dc83c15768998c3345c80d62c6f9d938b782e675467386?color=5a5a5a)
 in
in 
 Die Lösung lautet
Die Lösung lautet  und
und  Lösungsmöglichkeit B
Lösungsmöglichkeit B
(Einsetzungsverfahren) Erste Gleichung nach
Erste Gleichung nach  auflösen:
auflösen:

 in
in 
![\(\begin{array}[t]{rll}
2y+(3,5y)-12)-32&=&0\\[5pt]
5,5y-44&=&0 & \scriptsize \mid\;+44 \\[5pt]
5,5y&=&44 &\scriptsize \mid\;:5,5 \\[5pt]
y&=&8
\end{array}\)](https://mathjax.schullv.de/5a33bb0031a287a7b00f7aa92a9448c060464b25def698c0d0038b9818e0ae37?color=5a5a5a)
 in
in 
 Die Lösung lautet
Die Lösung lautet  und
und 
(Gleichsetzungsverfahren)
(Einsetzungsverfahren)
2.
3.
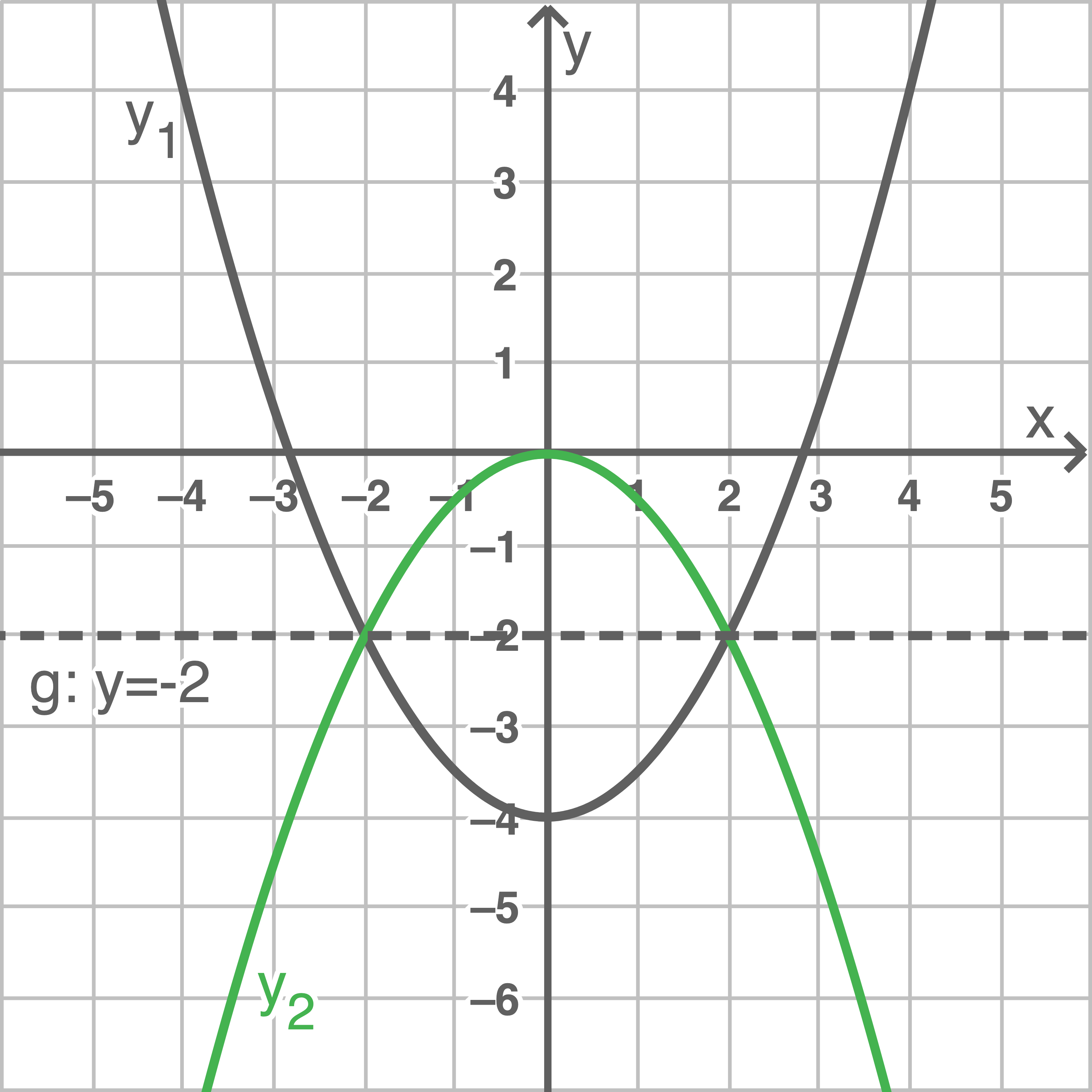
4.
Ist ein Dreieck rechtwinklig, gilt der Satz des Pythagoras:  Dreieck
Dreieck 
![\(\begin{array}[t]{rll}
(9\,\text{cm})^2+(12\,\text{cm})^2&=&(15\,\text{cm})^2\\[5pt]
81\,\text{cm}^2+144\,\text{cm}^2&=&225\,\text{cm}^2\\[5pt]
225\,\text{cm}^2&=&225\,\text{cm}^2
\end{array}\)](https://mathjax.schullv.de/099d76fc6674db528a03a4aeaf487aee6f912407afa16b0191a08a407e1aaae9?color=5a5a5a) Dreieck
Dreieck  ist also rechtwinklig. Die Überprüfung der anderen Dreiecke ist nicht mehr notwendig.
ist also rechtwinklig. Die Überprüfung der anderen Dreiecke ist nicht mehr notwendig.
5.
Mittelwert
Beim Mittelwert wird die Summe aller Werte durch deren Anzahl geteilt:
Temperaturunterschied
 Dabei muss auf das Vorzeichen geachtet werden, da
Dabei muss auf das Vorzeichen geachtet werden, da  gilt.
gilt.
6.
Es handelt sich um eine quadratische Gleichung, die zunächst umgeformt werden kann:
![\(\begin{array}[t]{rll}
0,5x^2-3x+4,5&=&0&\scriptsize \mid\;\cdot 2 \\[5pt]
x^2-6x+9&=&0\\[5pt]
\end{array}\)](https://mathjax.schullv.de/e371645eb16c9b10500db7b19d60c5562fbd15b329c15544ce27b23afd163758?color=5a5a5a) Die Gleichung kann mit der Lösungsformel gelöst werden:
Die Gleichung kann mit der Lösungsformel gelöst werden:
 Dabei gilt
Dabei gilt  und
und  Die Gleichung hat dann zwei Lösungen, wenn der Term unter der Wurzel (die Diskriminante
Die Gleichung hat dann zwei Lösungen, wenn der Term unter der Wurzel (die Diskriminante  ) größer Null ist:
) größer Null ist:

 Die Behauptung von Jano ist also falsch, da der Term unter der Wurzel gleich Null ist.
Die Behauptung von Jano ist also falsch, da der Term unter der Wurzel gleich Null ist.
7.
Im unteren Dreieck liegen alle Eckpunkte auf einem Thaleskreis. Es besitzt daher einen rechten Winkel.
Zudem ist es gleichschenklig. Wegen der Winkelsumme sind die anderen beiden Winkel daher groß.
Das obere Dreieck ist gleichseitig. Daher dort sind alle Innenwinkel gleich groß und somit
groß.
Das obere Dreieck ist gleichseitig. Daher dort sind alle Innenwinkel gleich groß und somit  groß.
Also gilt für die Größe von
groß.
Also gilt für die Größe von 

Zudem ist es gleichschenklig. Wegen der Winkelsumme sind die anderen beiden Winkel daher
8.
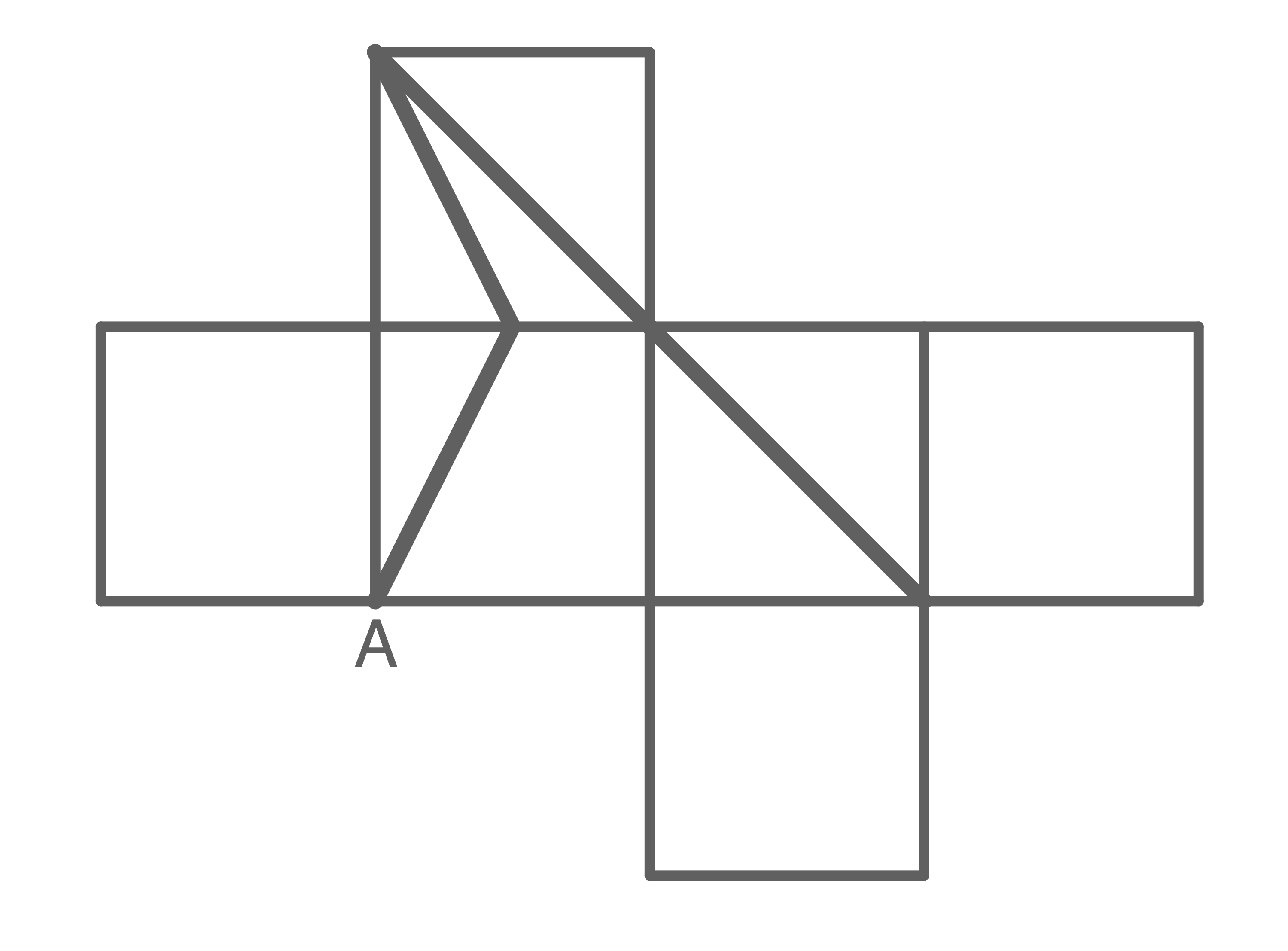
9.
Da die Haushöhe  parallel zur Höhe von
parallel zur Höhe von  ist, kann der Strahlensatz genutzt werden.
ist, kann der Strahlensatz genutzt werden.
![\(\begin{array}[t]{rll}
\dfrac{h}{4\,\text{m}+20\,\text{m}}&=&\dfrac{2\,\text{m}}{4\,\text{m}}\\[5pt]
\dfrac{h}{24\,\text{m}}&=&\dfrac{1}{2} &\scriptsize \mid\;\cdot 24\,\text{m} \\[5pt]
h&=&12\,\text{m}
\end{array}\)](https://mathjax.schullv.de/3f15b4b4fcc29ef07ecd169d56780a672c3d6d54fc122296dcadde7a321c31a7?color=5a5a5a) Das Haus ist also
Das Haus ist also  hoch.
hoch.
10.
Jede Karte wird mit der gleichen Wahrscheinlichkeit aufgedeckt. Es sind nur noch fünf Karten verdeckt, auf jeder dieser Karten kann die Sonne sein.
