Prüfungsteil B: Mit Hilfsmitteln
Aufgabe 3: Analysis (innermathematische Aufgabe)
Gegeben ist die Funktion  mit der Gleichung
mit der Gleichung  Die Abbildung zeigt den Graphen von
Die Abbildung zeigt den Graphen von 
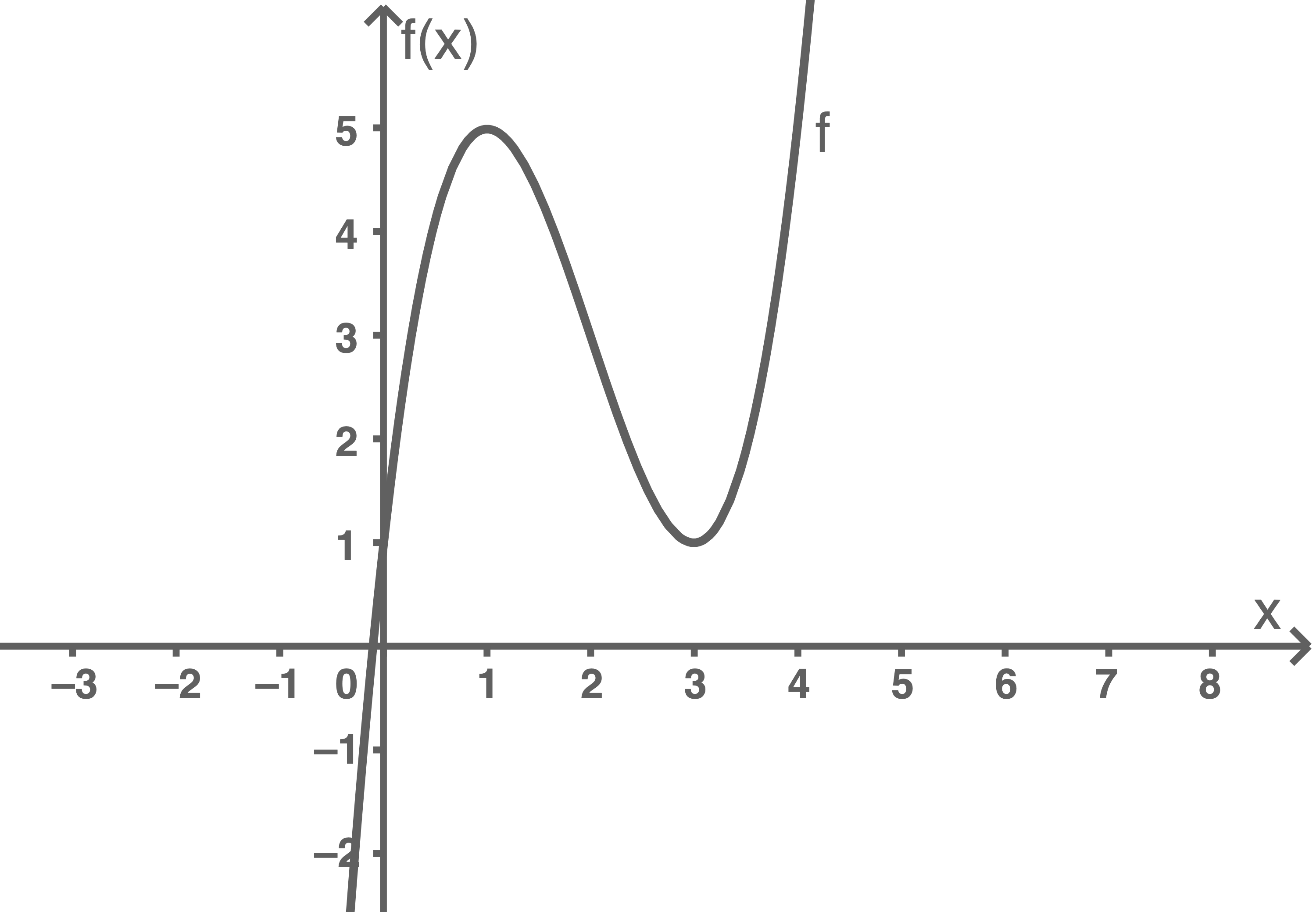

Abbildung
a)
Ermittle auf drei Nachkommastellen genau die Nullstelle der Funktion 
(2 Punkte)
b)
Ermittle rechnerisch den lokalen Hochpunkt und den lokalen Tiefpunkt des Graphen von 
(7 Punkte)
c)
Zeichne in die Abbildung die Sekante  durch die Punkte
durch die Punkte  und
und  ein.
Ermittle rechnerisch eine Gleichung dieser Sekante
ein.
Ermittle rechnerisch eine Gleichung dieser Sekante 
(6 Punkte)
d)
Ein Schüler möchte am Beispiel der Funktion  in einem Referat erklären, wie deren Ableitung
in einem Referat erklären, wie deren Ableitung  an einer Stelle
an einer Stelle  näherungsweise ermittelt werden kann. Dazu hat er eine Tabelle angelegt.
näherungsweise ermittelt werden kann. Dazu hat er eine Tabelle angelegt.
Gib an, um welche Stelle  es sich hier handelt.
Erkläre, warum die Tabellenwerte sich immer mehr der Ableitung
es sich hier handelt.
Erkläre, warum die Tabellenwerte sich immer mehr der Ableitung  annähern.
annähern.
| Term | Wert |
(4 Punkte)
e)
Gegeben ist nun zusätzlich die Funktion  mit der Gleichung
mit der Gleichung
 Ermittle, durch welche Transformationen der Graph der Funktion
Ermittle, durch welche Transformationen der Graph der Funktion  aus dem Graphen der Funktion
aus dem Graphen der Funktion  hervorgeht, und beschreibe deine Vorgehensweise.
hervorgeht, und beschreibe deine Vorgehensweise.
(5 Punkte)
Aufgabe 4: Analysis (kontextbezogene Aufgabe)
Früher wurden in den Städten auf Hügeln oder kleineren Bergen Wassertürme gebaut. Durch das in den Türmen gespeicherte Wasser konnte ein ausreichender Wasserdruck für die Versorgung der Wohnungen mit Trinkwasser sichergestellt werden.
Im Folgenden soll die Wassermenge im Speicher eines Wasserturms untersucht werden.
Um den nötigen Wasserdruck zu gewährleisten, soll dafür gesorgt werden, dass ständig mindestens  Wasser (Sollwert) im Speicher des Turmes vorhanden sind. Die maximale Füllmenge beträgt
Wasser (Sollwert) im Speicher des Turmes vorhanden sind. Die maximale Füllmenge beträgt  Für einen bestimmten Tag wird die Wassermenge im Speicher des Turmes im Zeitraum von 6:00 Uhr bis 7:30 Uhr für
Für einen bestimmten Tag wird die Wassermenge im Speicher des Turmes im Zeitraum von 6:00 Uhr bis 7:30 Uhr für  durch die Funktion
durch die Funktion  mit der Gleichung
mit der Gleichung
 modelliert. Dabei bezeichnet
modelliert. Dabei bezeichnet  die Zeit in Stunden, die seit 6:00 Uhr vergangen ist, und
die Zeit in Stunden, die seit 6:00 Uhr vergangen ist, und  die Wassermenge im Speicher des Turmes in
die Wassermenge im Speicher des Turmes in  Der Graph der Funktion
Der Graph der Funktion  ist in der folgenden Abbildung dargestellt.
ist in der folgenden Abbildung dargestellt.
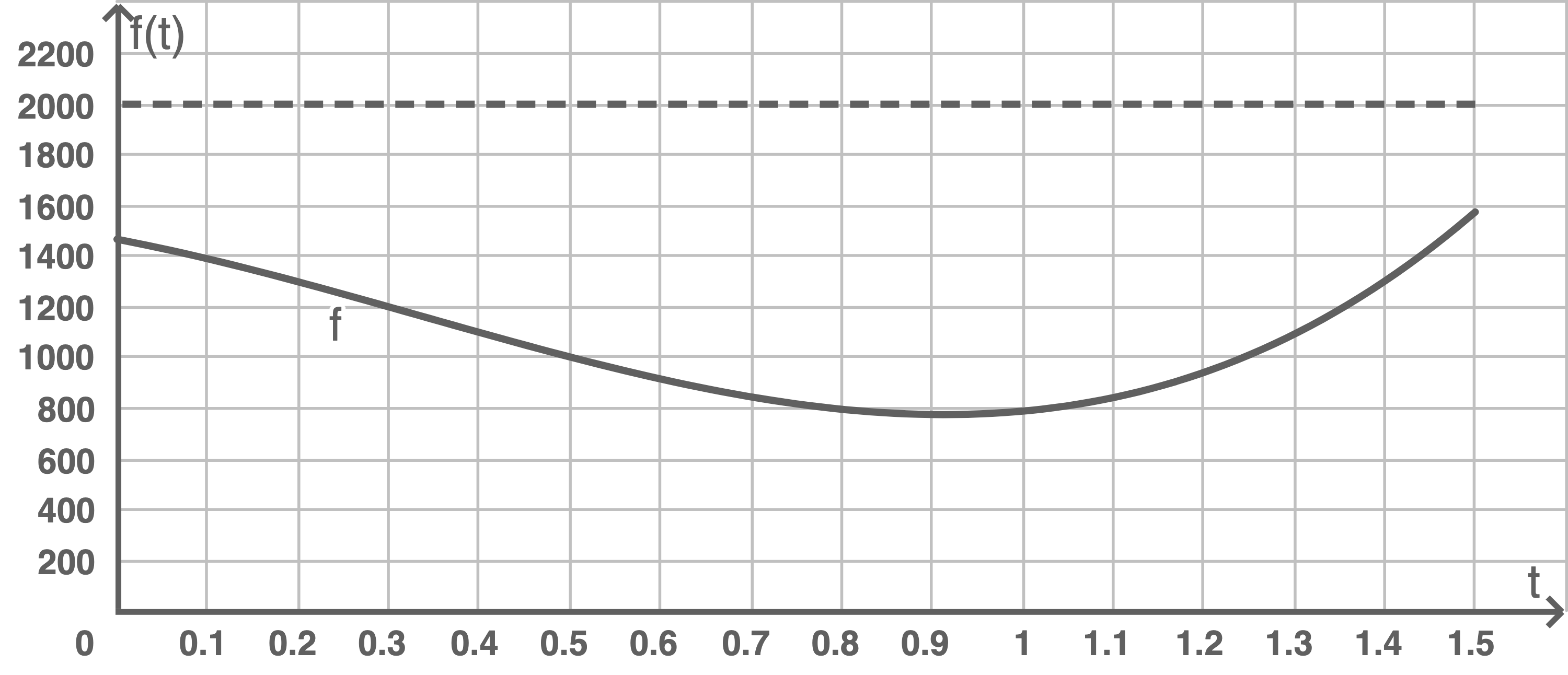 Mit der Funktion
Mit der Funktion  ist es möglich, die folgenden Aufgabenstellungen zu bearbeiten.
ist es möglich, die folgenden Aufgabenstellungen zu bearbeiten.

Abbildung
a)
(1) Zeige, dass um 7:00 Uhr nur noch  Wasser im Speicher des Turmes vorhanden sind.
Wasser im Speicher des Turmes vorhanden sind.
(2) Ermittle näherungsweise die Zeiträume, in denen die Wassermenge über dem Sollwert von  liegt.
liegt.
(2 + 4 Punkte)
b)
Ermittle rechnerisch den Zeitpunkt, zu dem die Wassermenge im Speicher des Turmes minimal ist.
Berechne, um wie viele  Wasser der Sollwert zu diesem Zeitpunkt unterschritten wird.
Wasser der Sollwert zu diesem Zeitpunkt unterschritten wird.
(8 Punkte)
c)
Berechne  und
und  und interpretiere die berechneten Werte im Sachzusammenhang.
und interpretiere die berechneten Werte im Sachzusammenhang.
(4 Punkte)
d)
Gegeben ist nun zusätzlich die Funktion  mit der Gleichung
mit der Gleichung

(1) Zeichne den Graphen von  in die Abbildung ein.
in die Abbildung ein.
(2) Erkläre, welche Bedeutung die Funktionswerte  mit
mit  im Sachzusammenhang haben.
im Sachzusammenhang haben.
(4 + 2 Punkte)
Lösung 3
a)
menu  3: Algebra
3: Algebra  1: Löse
1: Löse
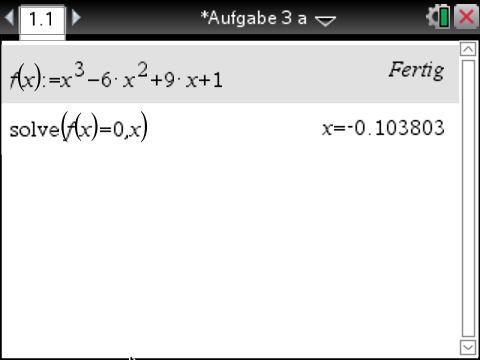
b)
1. Schritt: Funktion ableiten
![\(\begin{array}[t]{rll}
f(x)&=& x^3-6x^2+9x+1 & \\[5pt]
f](https://mathjax.schullv.de/16f0c9b1d90e6a41e6d64c8baf23fb01582bb2837365ca56eb76d9fa5dbcb04a?color=5a5a5a) 2. Schritt: Notwendige Bedingung überprüfen
2. Schritt: Notwendige Bedingung überprüfen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/c57d613e1fd2de24cbb9a863898f0f3404ea01ba7d834e6965d87ca8430d7fff?color=5a5a5a)
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{(-4)}{2}\pm\sqrt{\left(\dfrac{-4}{2}\right)^2-3}\\[5pt]
&=& 2\pm\sqrt{1} \\[5pt]
x_1&=& 1 \\[5pt]
x_2&=& 3 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/86b21766942801ca49fe7d05c59f430b3f603251ed1d67f232422683f0c7ff42?color=5a5a5a) 3. Schritt: Vorzeichenwechsel-Kriterium überprüfen
3. Schritt: Vorzeichenwechsel-Kriterium überprüfen


 An der Stelle
An der Stelle  liegt ein Vorzeichenwechsel von
liegt ein Vorzeichenwechsel von  von + nach - und damit ein lokaler Hochpunkt vor.
von + nach - und damit ein lokaler Hochpunkt vor.
An der Stelle liegt ein Vorzeichenwechsel von
liegt ein Vorzeichenwechsel von  von - nach + und damit ein lokaler Tiefpunkt vor.
4. Schritt:
von - nach + und damit ein lokaler Tiefpunkt vor.
4. Schritt:  -Werte bestimmen
-Werte bestimmen

 Die Funktion hat einen lokalen Hochpunkt bei
Die Funktion hat einen lokalen Hochpunkt bei  und einen lokalen Tiefpunkt bei
und einen lokalen Tiefpunkt bei  .
.
An der Stelle
c)
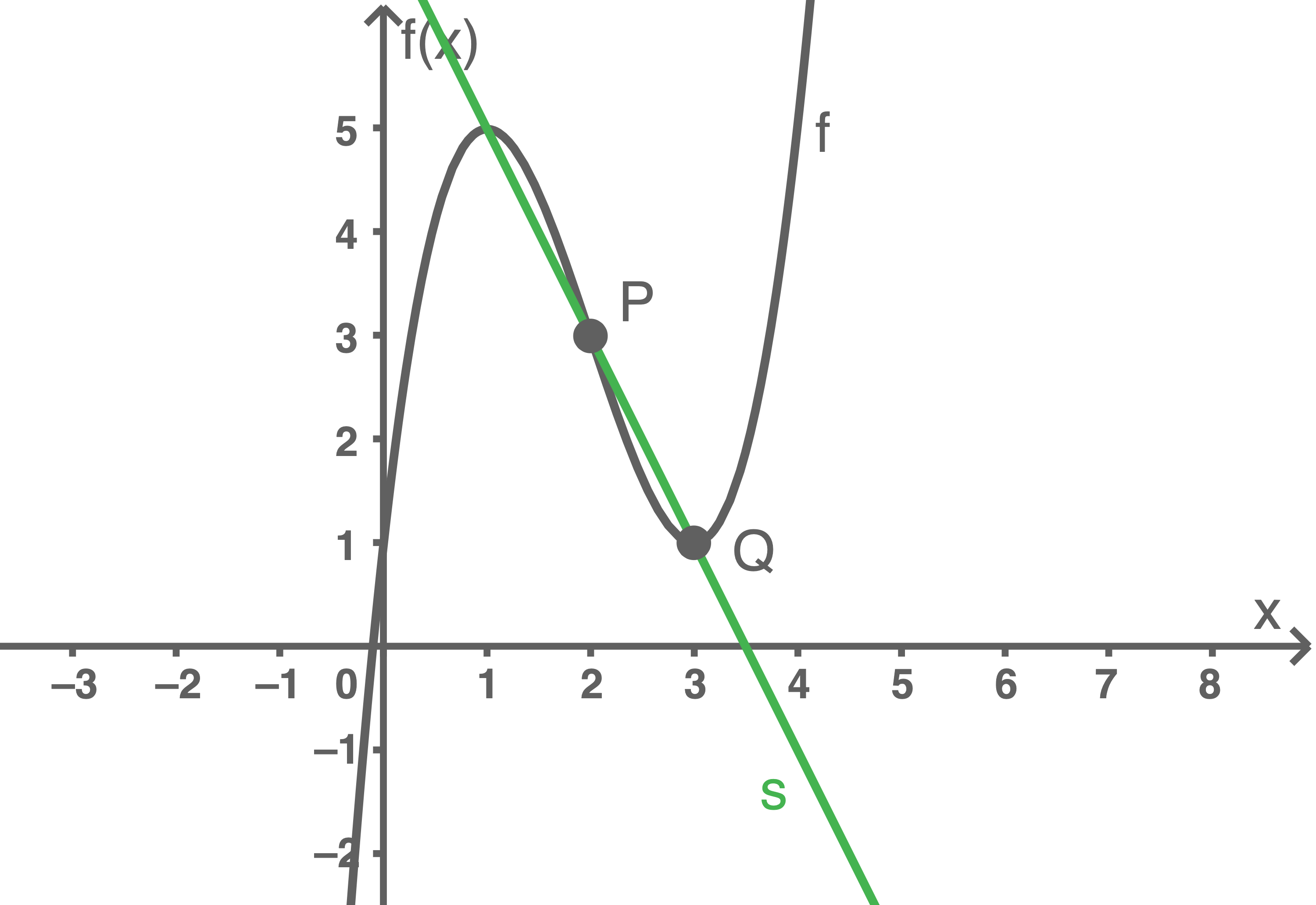
d)
Es handelt sich um die Stelle  Der Grenzwert
Der Grenzwert  definiert die Ableitung von
definiert die Ableitung von  an der Stelle
an der Stelle  Die Tabellenwerte starten bei dem Wert
Die Tabellenwerte starten bei dem Wert  und nähern sich dann immer mehr dem Wert
und nähern sich dann immer mehr dem Wert  an. Damit nähern sich die Tabellenwerte auch immer mehr der Ableitung
an. Damit nähern sich die Tabellenwerte auch immer mehr der Ableitung  an.
an.
e)
Zeichnet man beide Graphen mit dem CAS, kann man erkennen, dass der Graph von  den selben Verlauf wie der Graph von
den selben Verlauf wie der Graph von  hat. Er ist im Vergleich zu
hat. Er ist im Vergleich zu  nach unten und nach rechts verschoben.
nach unten und nach rechts verschoben.
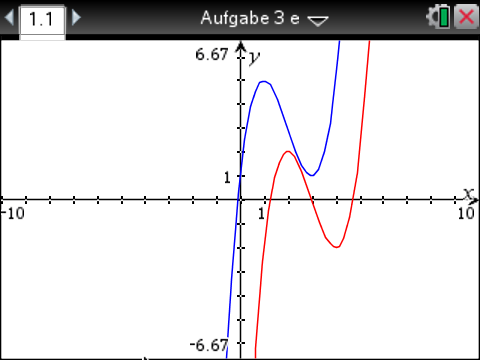 Um die genaue Verschiebung zu berechnen, werden die Koordinaten der Extrempunkte verglichen.
Um die genaue Verschiebung zu berechnen, werden die Koordinaten der Extrempunkte verglichen.


 und
und  Der Vergleich der Koordinaten zeigt, dass der Graph der Funktion
Der Vergleich der Koordinaten zeigt, dass der Graph der Funktion  aus dem Graph der Funktion
aus dem Graph der Funktion  hervorgeht, indem der Graph um
hervorgeht, indem der Graph um  Einheit in positive
Einheit in positive  -Richtung und um
-Richtung und um  Einheiten in negative
Einheiten in negative  -Richtung verschoben wird.
-Richtung verschoben wird.

6. Graph analysieren  3: Maximum
3: Maximum
6. Graph analysieren  2: Minimum
2: Minimum
Der CAS liefert Lösung 4
a)
(1)
Der CAS liefert  Eine Stunde nach Messbeginn, also um 7:00 Uhr, beträgt der Wasserstand im Turm
Eine Stunde nach Messbeginn, also um 7:00 Uhr, beträgt der Wasserstand im Turm  .
.
(2)
Zunächst werden die Stellen berechnet, an denen die Wassermenge genau dem Sollwert entspricht.
Der CAS liefert für  die Lösungen
die Lösungen 
 und
und  wobei
wobei  nicht im betrachteten Zeitraum liegt.
Der Abbildung kann entnommen werden, dass der Wasserstand zwischen
nicht im betrachteten Zeitraum liegt.
Der Abbildung kann entnommen werden, dass der Wasserstand zwischen  und
und  unterhalb des Sollwerts liegt. Daher liegt der Wasserstand ungefähr zwischen 6:00 Uhr und 6:30 Uhr sowie zwischen 7:15 Uhr und 7:30 Uhr über dem Sollwert.
unterhalb des Sollwerts liegt. Daher liegt der Wasserstand ungefähr zwischen 6:00 Uhr und 6:30 Uhr sowie zwischen 7:15 Uhr und 7:30 Uhr über dem Sollwert.
b)
Zeitpunkt der minimalen Wassermenge bestimmen
1. Schritt: Ableitung berechnen

 2. Schritt: Notwendige Bedingung anwenden
Da
2. Schritt: Notwendige Bedingung anwenden
Da  außerhalb des Definitionsbereiches der Funktion liegt, wird im Folgenden nur der Wert
außerhalb des Definitionsbereiches der Funktion liegt, wird im Folgenden nur der Wert  betrachtet.
3. Schritt: Vorzeichenwechsel-Kriterium überprüfen
betrachtet.
3. Schritt: Vorzeichenwechsel-Kriterium überprüfen

 An der Stelle
An der Stelle  liegt ein Vorzeichenwechsel von - nach + und damit ein lokaler Tiefpunkt vor. Wegen
liegt ein Vorzeichenwechsel von - nach + und damit ein lokaler Tiefpunkt vor. Wegen  und
und  liegt bei
liegt bei  sogar ein globaler Tiefpunkt vor.
sogar ein globaler Tiefpunkt vor.


 Folglich ist die Wassermenge um ca. 6:55 Uhr minimal.
Unterschreitung des Sollwerts berechnen
Folglich ist die Wassermenge um ca. 6:55 Uhr minimal.
Unterschreitung des Sollwerts berechnen

 Der minimale Wasserstand im Speicher des Turms liegt
Der minimale Wasserstand im Speicher des Turms liegt  unter dem Sollwert.
unter dem Sollwert.
c)
d)
(1)
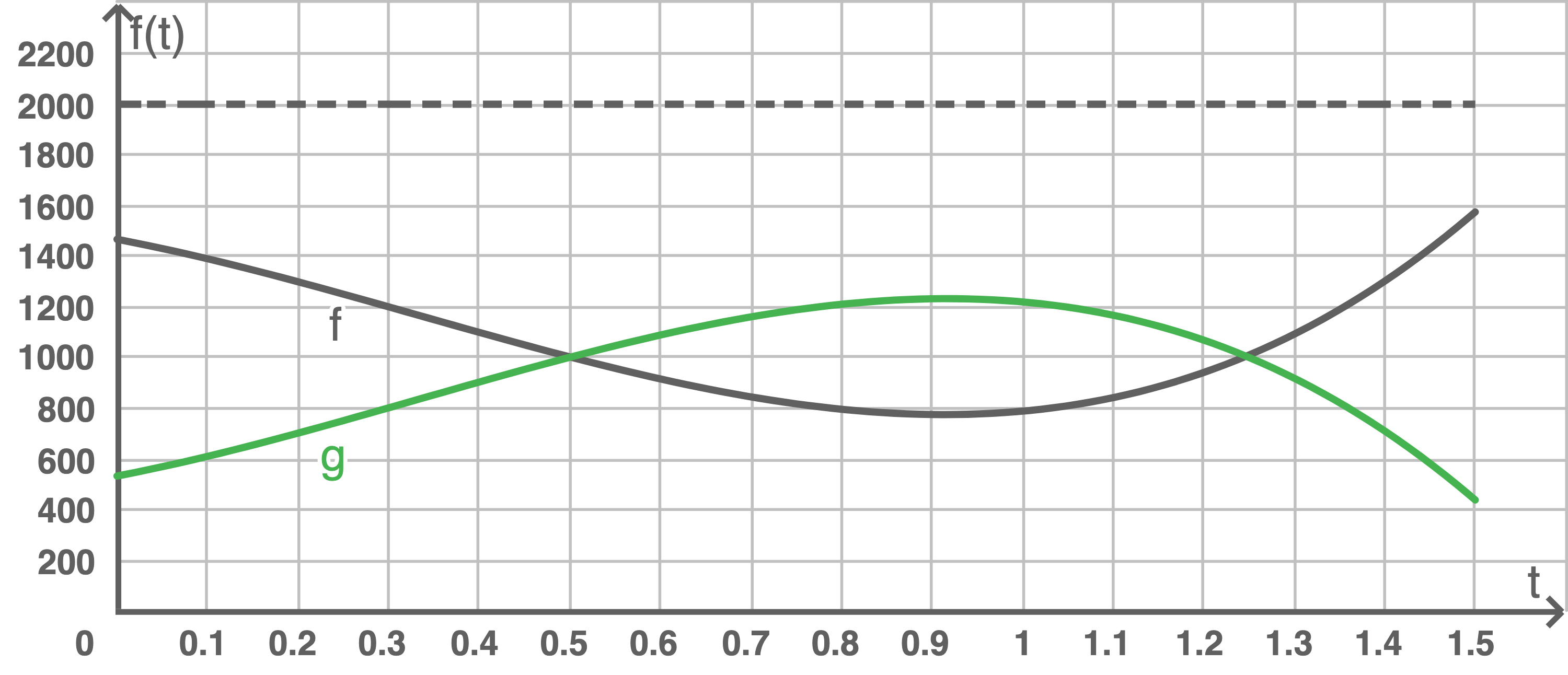
(2)
Die Funktionswerte von  und
und  an einer Stelle
an einer Stelle  ergeben in Summe immer den Wert
ergeben in Summe immer den Wert  Das entspricht genau der maximalen Füllmenge des Wasserturms. Der Graph der Funktion
Das entspricht genau der maximalen Füllmenge des Wasserturms. Der Graph der Funktion  gibt die Wassermenge, die zu einem Zeitpunkt
gibt die Wassermenge, die zu einem Zeitpunkt  im Wasserturm vorhanden ist, an.
Der Graph der Funktion
im Wasserturm vorhanden ist, an.
Der Graph der Funktion  gibt folglich die Größe des freien Raums im Wasserturm zum Zeitpunkt
gibt folglich die Größe des freien Raums im Wasserturm zum Zeitpunkt  an.
an.
Lösung 3
a)
Analysis  G-Solve
G-Solve  Root
Root
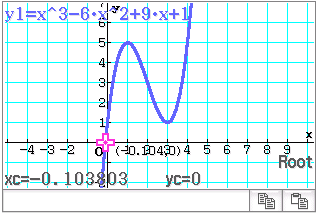
b)
1. Schritt: Funktion ableiten
![\(\begin{array}[t]{rll}
f(x)&=& x^3-6x^2+9x+1 & \\[5pt]
f](https://mathjax.schullv.de/16f0c9b1d90e6a41e6d64c8baf23fb01582bb2837365ca56eb76d9fa5dbcb04a?color=5a5a5a) 2. Schritt: Notwendige Bedingung überprüfen
2. Schritt: Notwendige Bedingung überprüfen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/c57d613e1fd2de24cbb9a863898f0f3404ea01ba7d834e6965d87ca8430d7fff?color=5a5a5a)
![\(\begin{array}[t]{rll}
x_{1,2}&=& -\dfrac{(-4)}{2}\pm\sqrt{\left(\dfrac{-4}{2}\right)^2-3}\\[5pt]
&=& 2\pm\sqrt{1} \\[5pt]
x_1&=& 1 \\[5pt]
x_2&=& 3 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/86b21766942801ca49fe7d05c59f430b3f603251ed1d67f232422683f0c7ff42?color=5a5a5a) 3. Schritt: Vorzeichenwechsel-Kriterium überprüfen
3. Schritt: Vorzeichenwechsel-Kriterium überprüfen


 An der Stelle
An der Stelle  liegt ein Vorzeichenwechsel von
liegt ein Vorzeichenwechsel von  von + nach - und damit ein lokaler Hochpunkt vor.
von + nach - und damit ein lokaler Hochpunkt vor.
An der Stelle liegt ein Vorzeichenwechsel von
liegt ein Vorzeichenwechsel von  von - nach + und damit ein lokaler Tiefpunkt vor.
4. Schritt:
von - nach + und damit ein lokaler Tiefpunkt vor.
4. Schritt:  -Werte bestimmen
-Werte bestimmen

 Die Funktion hat einen lokalen Hochpunkt bei
Die Funktion hat einen lokalen Hochpunkt bei  und einen lokalen Tiefpunkt bei
und einen lokalen Tiefpunkt bei  .
.
An der Stelle
c)

d)
Es handelt sich um die Stelle  Der Grenzwert
Der Grenzwert  definiert die Ableitung von
definiert die Ableitung von  an der Stelle
an der Stelle  Die Tabellenwerte starten bei dem Wert
Die Tabellenwerte starten bei dem Wert  und nähern sich dann immer mehr dem Wert
und nähern sich dann immer mehr dem Wert  an. Damit nähern sich die Tabellenwerte auch immer mehr der Ableitung
an. Damit nähern sich die Tabellenwerte auch immer mehr der Ableitung  an.
an.
e)
Zeichnet man beide Graphen mit dem CAS, kann man erkennen, dass der Graph von  den selben Verlauf wie der Graph von
den selben Verlauf wie der Graph von  hat. Er ist im Vergleich zu
hat. Er ist im Vergleich zu  nach unten und nach rechts verschoben.
nach unten und nach rechts verschoben.
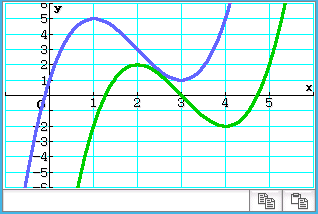 Um die genaue Verschiebung zu berechnen, werden die Koordinaten der Extrempunkte verglichen.
Um die genaue Verschiebung zu berechnen, werden die Koordinaten der Extrempunkte verglichen.


 und
und  Der Vergleich der Koordinaten zeigt, dass der Graph der Funktion
Der Vergleich der Koordinaten zeigt, dass der Graph der Funktion  aus dem Graph der Funktion
aus dem Graph der Funktion  hervorgeht, indem der Graph um
hervorgeht, indem der Graph um  Einheit in positive
Einheit in positive  -Richtung und um
-Richtung und um  Einheiten in negative
Einheiten in negative  -Richtung verschoben wird.
-Richtung verschoben wird.

Analysis  G-Solve
G-Solve  Max
Max
Analysis  G-Solve
G-Solve  Min
Min
Der CAS liefert Lösung 4
a)
(1)
Der CAS liefert  Eine Stunde nach Messbeginn, also um 7:00 Uhr, beträgt der Wasserstand im Turm
Eine Stunde nach Messbeginn, also um 7:00 Uhr, beträgt der Wasserstand im Turm  .
.
(2)
Zunächst werden die Stellen berechnet, an denen die Wassermenge genau dem Sollwert entspricht.
Der CAS liefert für  die Lösungen
die Lösungen 
 und
und  wobei
wobei  nicht im betrachteten Zeitraum liegt.
Der Abbildung kann entnommen werden, dass der Wasserstand zwischen
nicht im betrachteten Zeitraum liegt.
Der Abbildung kann entnommen werden, dass der Wasserstand zwischen  und
und  unterhalb des Sollwerts liegt. Daher liegt der Wasserstand ungefähr zwischen 6:00 Uhr und 6:30 Uhr sowie zwischen 7:15 Uhr und 7:30 Uhr über dem Sollwert.
unterhalb des Sollwerts liegt. Daher liegt der Wasserstand ungefähr zwischen 6:00 Uhr und 6:30 Uhr sowie zwischen 7:15 Uhr und 7:30 Uhr über dem Sollwert.
b)
Zeitpunkt der minimalen Wassermenge bestimmen
1. Schritt: Ableitung berechnen

 2. Schritt: Notwendige Bedingung anwenden
Da
2. Schritt: Notwendige Bedingung anwenden
Da  außerhalb des Definitionsbereiches der Funktion liegt, wird im Folgenden nur der Wert
außerhalb des Definitionsbereiches der Funktion liegt, wird im Folgenden nur der Wert  betrachtet.
3. Schritt: Vorzeichenwechsel-Kriterium überprüfen
betrachtet.
3. Schritt: Vorzeichenwechsel-Kriterium überprüfen

 An der Stelle
An der Stelle  liegt ein Vorzeichenwechsel von - nach + und damit ein lokaler Tiefpunkt vor. Wegen
liegt ein Vorzeichenwechsel von - nach + und damit ein lokaler Tiefpunkt vor. Wegen  und
und  liegt bei
liegt bei  sogar ein globaler Tiefpunkt vor.
sogar ein globaler Tiefpunkt vor.


 Folglich ist die Wassermenge um ca. 6:55 Uhr minimal.
Unterschreitung des Sollwerts berechnen
Folglich ist die Wassermenge um ca. 6:55 Uhr minimal.
Unterschreitung des Sollwerts berechnen

 Der minimale Wasserstand im Speicher des Turms liegt
Der minimale Wasserstand im Speicher des Turms liegt  unter dem Sollwert.
unter dem Sollwert.
c)
d)
(1)

(2)
Die Funktionswerte von  und
und  an einer Stelle
an einer Stelle  ergeben in Summe immer den Wert
ergeben in Summe immer den Wert  Das entspricht genau der maximalen Füllmenge des Wasserturms. Der Graph der Funktion
Das entspricht genau der maximalen Füllmenge des Wasserturms. Der Graph der Funktion  gibt die Wassermenge, die zu einem Zeitpunkt
gibt die Wassermenge, die zu einem Zeitpunkt  im Wasserturm vorhanden ist, an.
Der Graph der Funktion
im Wasserturm vorhanden ist, an.
Der Graph der Funktion  gibt folglich die Größe des freien Raums im Wasserturm zum Zeitpunkt
gibt folglich die Größe des freien Raums im Wasserturm zum Zeitpunkt  an.
an.