Prüfungsteil B: Mit Hilfsmitteln
Aufgabe 3
Gegeben ist die Funktion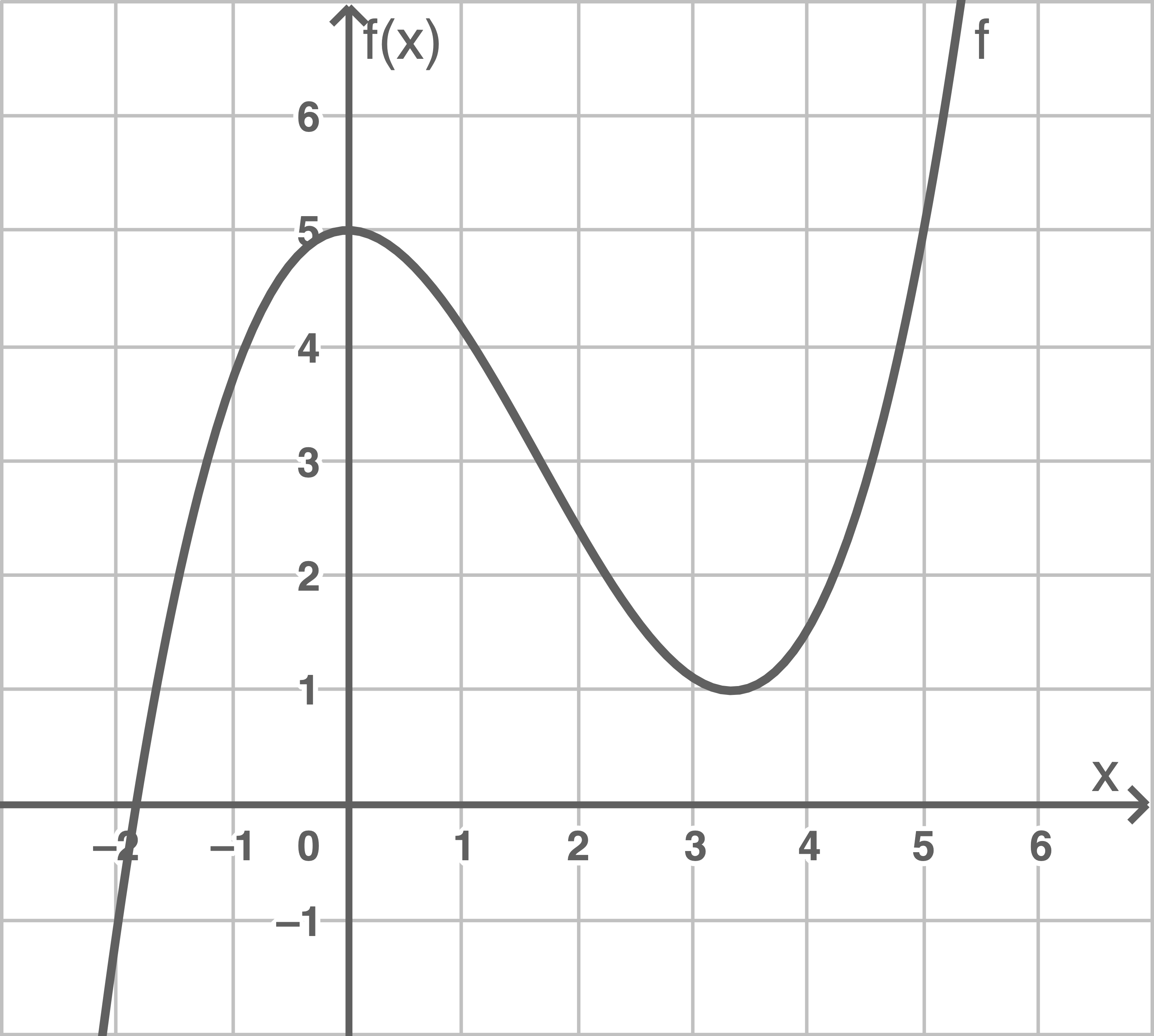
Abbildung 1
a)
Prüfe, ob der Punkt  auf dem Graphen der Funktion
auf dem Graphen der Funktion  liegt.
liegt.
(2 Punkte)
b)
Gib  an und bestimme rechnerisch - ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden - die Koordinaten der lokalen Extrempunkte des Graphen von
an und bestimme rechnerisch - ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden - die Koordinaten der lokalen Extrempunkte des Graphen von  [Zur Kontrolle: Der lokale Tiefpunkt liegt an der Stelle
[Zur Kontrolle: Der lokale Tiefpunkt liegt an der Stelle  ]
]
(7 Punkte)
c)
(1)
Ermittle rechnerisch eine Gleichung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  [Zur Kontrolle:
[Zur Kontrolle:  ]
]
(2)
Die Tangente  und der Graph von
und der Graph von  besitzen einen weiteren gemeinsamen Punkt
besitzen einen weiteren gemeinsamen Punkt  Bestimme die Koordinaten von
Bestimme die Koordinaten von 
(4 + 3 Punkte)
d)
Für eine Funktion  gilt:
gilt: 
(1)
Begründe, warum die Graphen von  und
und  identisch sind.
identisch sind.
(2)
Wenn der Graph von  genau drei Schnittpunkte mit der
genau drei Schnittpunkte mit der  -Achse besitzen soll, dann dürfen für
-Achse besitzen soll, dann dürfen für  nur Werte aus einem bestimmten Bereich eingesetzt werden.
Gib diesen Bereich an.
nur Werte aus einem bestimmten Bereich eingesetzt werden.
Gib diesen Bereich an.
(2 + 3 Punkte)
e)
Die Abbildung 2 zeigt den Graphen einer Funktion  mit
mit 
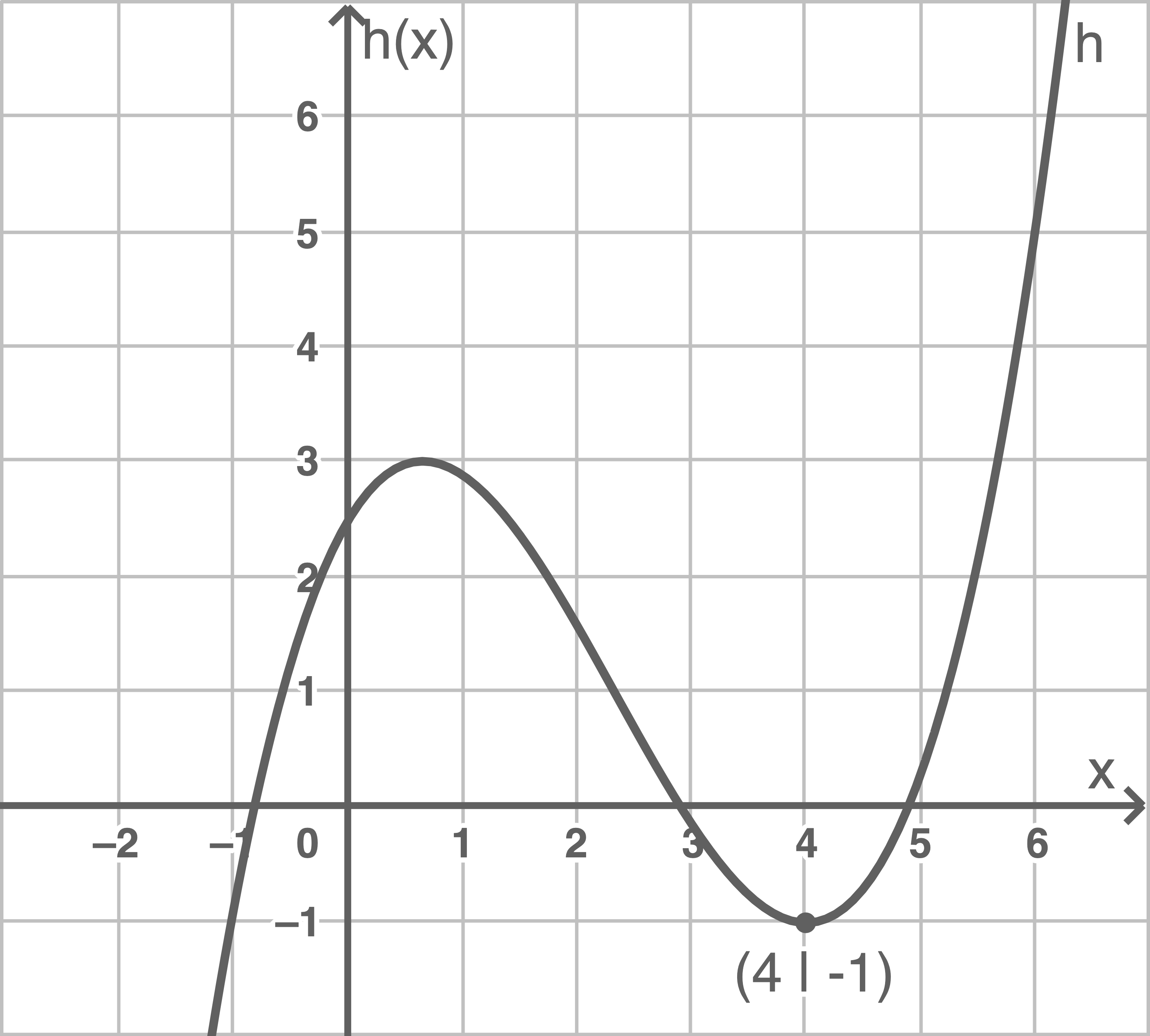 Ermittle
Ermittle  und
und 

Abbildung 2
(3 Punkte)
Aufgabe 4
Ein „Pumptrack“ ist eine speziell geschaffene Mountainbike-Strecke. Auf einem Pumptrack ist es das Ziel, am Rad allein durch Heben und Senken des Körpers Geschwindigkeit aufzubauen. Das seitliche Profil für einen Abschnitt eines Pumptracks wird für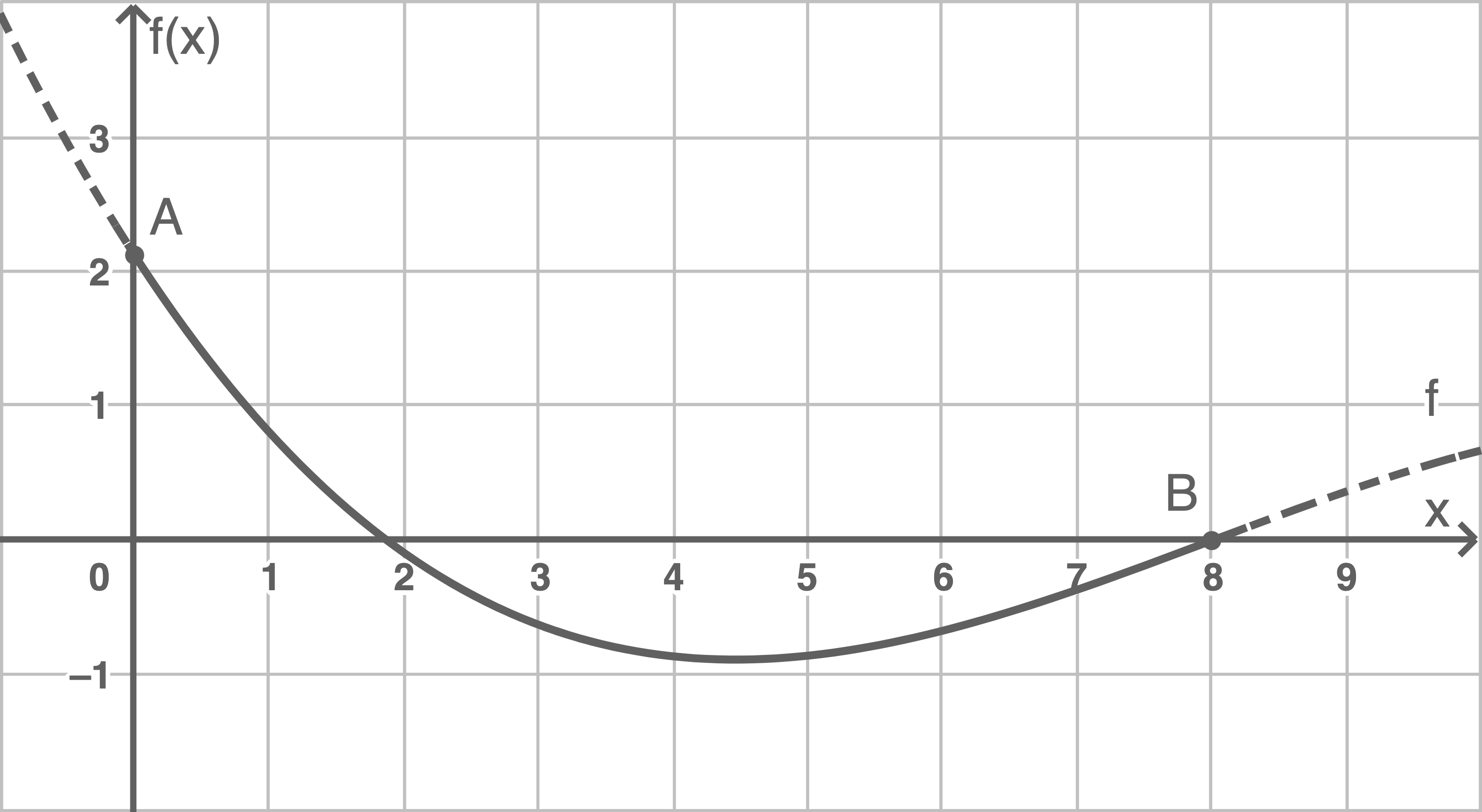
Abbildung 1
a)
(1)
Gib die genaue Höhe des Punktes A über dem Niveau des umgebenden Geländes an.
(2)
Die durchschnittliche Steigung zwischen dem Punkt A und dem Punkt B (siehe Abbildung 1) wird mit -0,265 angegeben.
Prüfe diese Angabe.
(3)
Erkläre, warum die durchschnittliche Steigung nur wenig über den Verlauf des Pumptrack-Abschnitts aussagt.
(4)
Die durchschnittliche Steigung -0,265 kommt auch als Steigung in einem Punkt des seitlichen Profils vor.
Gib  an und berechne die Koordinaten dieses Punktes.
an und berechne die Koordinaten dieses Punktes.
(1 + 3 + 2 + 4 Punkte)
b)
Bestimme rechnerisch - ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden -, wie tief unterhalb des Niveaus des umgebenden Geländes der niedrigste Punkt des Pumptrack-Abschnitts liegt.
Das seitliche Profil für den weiteren Verlauf des Pumptracks wird für
(7 Punkte)
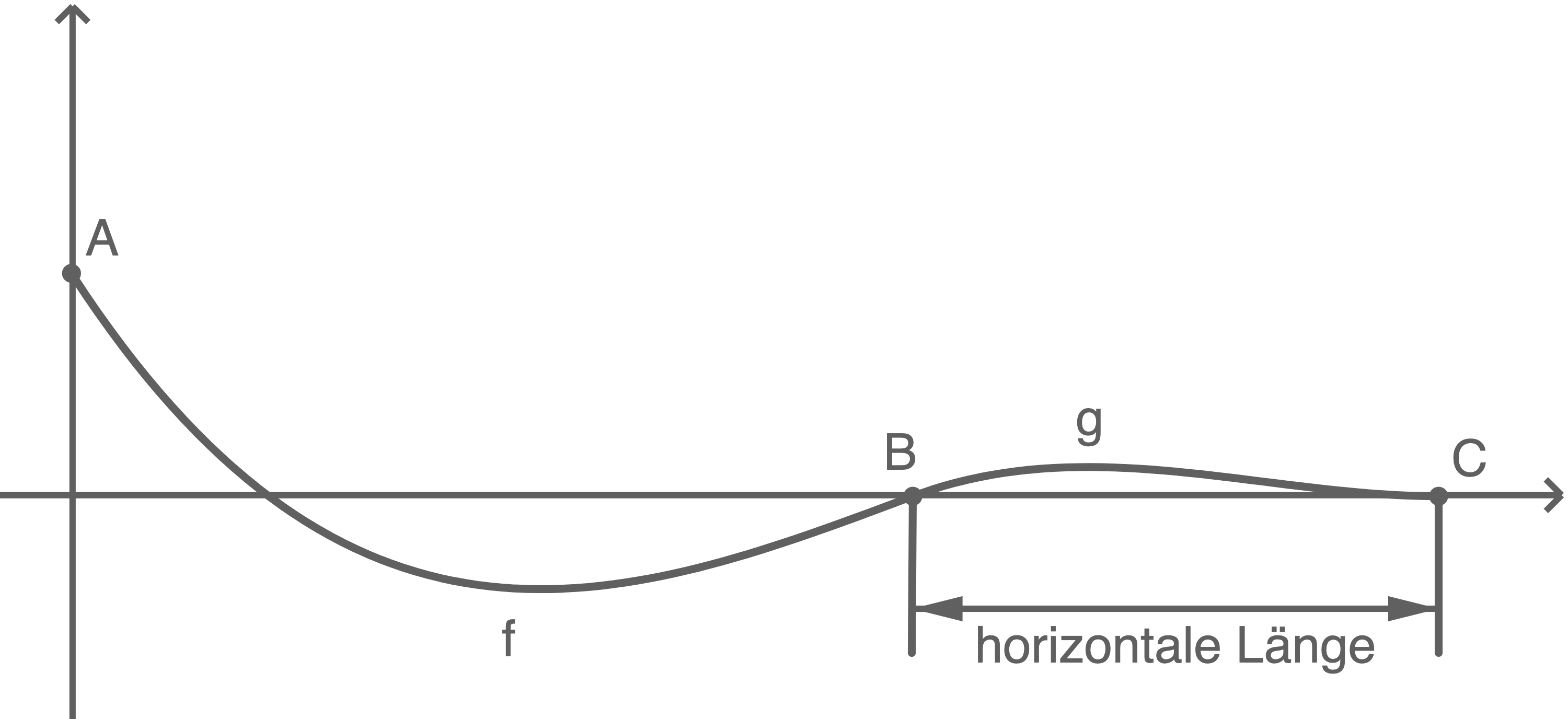
Abbildung 2
c)
(1)
Für einen glatten Übergang müssen die Graphen der Funktionen  und
und  knickfrei ineinander übergehen.
[„An einer Stelle knickfrei ineinander übergehen“ bedeutet: An dieser Stelle besitzen die Funktionen den gleichen Funktionswert und die gleiche Steigung.]
Weise rechnerisch nach, dass die Graphen der beiden Funktionen
knickfrei ineinander übergehen.
[„An einer Stelle knickfrei ineinander übergehen“ bedeutet: An dieser Stelle besitzen die Funktionen den gleichen Funktionswert und die gleiche Steigung.]
Weise rechnerisch nach, dass die Graphen der beiden Funktionen  und
und  an der Stelle
an der Stelle  knickfrei ineinander übergehen.
knickfrei ineinander übergehen.
(2)
Ermittle rechnerisch die horizontale Länge des zweiten Abschnitts (siehe Abbildung 2).
(4 + 3 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Aufgabe 3
a)
b)
1. Schritt:  angeben
angeben
![\(\begin{array}[t]{rll}
f(x)&=&\dfrac{27}{125}\cdot x^3-\dfrac{27}{25}\cdot x^2+5 \\[5pt]
f](https://mathjax.schullv.de/daa4f372821cd87ab9e2ccd96d04d0756e4f980e1ae6ab67419ed334be36c43c?color=5a5a5a) 2. Schritt:
2. Schritt:  setzen
setzen
![\(\begin{array}[t]{rll}
\dfrac{81}{125} \cdot x^2 - \dfrac{54}{25} \cdot x&=& 0 &\quad \scriptsize \\[5pt]
x\cdot \left(\dfrac{81}{125} \cdot x - \dfrac{54}{25}\right)&=& 0&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/9512952fb78b7a03f0fbafa29781fede9f244932c68d1e7927ab993270e749b9?color=5a5a5a) Mit dem Satz des Nullprodukts folgt
Mit dem Satz des Nullprodukts folgt  Für die zweite Nullstelle gilt:
Für die zweite Nullstelle gilt:
![\(\begin{array}[t]{rll}
\dfrac{81}{125} \cdot x_2 - \dfrac{54}{25}&=& 0\quad \scriptsize \mid\; +\dfrac{54}{25}\\[5pt]
\dfrac{81}{125} \cdot x_2 &=& \dfrac{54}{25} \quad \scriptsize \mid\; :\dfrac{81}{125} \\[5pt]
x_2&=& \dfrac{10}{3}
\end{array}\)](https://mathjax.schullv.de/84a8b9346c53eb25b8023ebe0a122f5bae032519cd3ea407d2db902376f6c2f7?color=5a5a5a) 3. Schritt: Das Vorzeichenwechsel-Kriterium anwenden
3. Schritt: Das Vorzeichenwechsel-Kriterium anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/467533c23932946bf5dfac804810b437bdc2b8f53dc64ee497640bbddc191516?color=5a5a5a) An der Stelle
An der Stelle  liegt also ein Vorzeichenwechsel von positiven zu negativen Funktionswerten von
liegt also ein Vorzeichenwechsel von positiven zu negativen Funktionswerten von  und damit ein lokales Maximum von
und damit ein lokales Maximum von  vor. An der Stelle
vor. An der Stelle  liegt ein Vorzeichenwechsel von negativen zu positiven Funktionswerten von
liegt ein Vorzeichenwechsel von negativen zu positiven Funktionswerten von  und damit ein lokales Minimum von
und damit ein lokales Minimum von  vor.
4. Schritt:
vor.
4. Schritt:  -Koordinaten berechnen
-Koordinaten berechnen
![\(\begin{array}[t]{rll}
f(0)&=& \dfrac{27}{125}\cdot 0^3-\dfrac{27}{25}\cdot 0^2+5&\quad \scriptsize \\[5pt]
&=& 5
\end{array}\)](https://mathjax.schullv.de/01a76cd3f49e64a31d08081ec2069cb7fc0f920b418073d056fa50d49bd504e1?color=5a5a5a) Daraus folgt, dass
Daraus folgt, dass  der lokale Hochpunkt und
der lokale Hochpunkt und  der lokale Tiefpunkt des Graphen von
der lokale Tiefpunkt des Graphen von  ist.
ist.
c)
(1)
Form einer Tangentengleichung:  1. Schritt: Steigung
1. Schritt: Steigung  an der Stelle
an der Stelle  berechnen
berechnen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/1c58a65f4067b7b0429906408bd1a138ea0353cd307469dce44dff6fe90c7521?color=5a5a5a) 2. Schritt:
2. Schritt:  -Koordinate von Punkt
-Koordinate von Punkt  berechnen
berechnen
![\(\begin{array}[t]{rll}
f(5)&=& \dfrac{27}{125}\cdot 5^3-\dfrac{27}{25}\cdot 5^2+5 &\quad \scriptsize \\[5pt]
f(5)&=& 5 = y
\end{array}\)](https://mathjax.schullv.de/ed3c16bd7e16524546126b9ce7d567b34110c3feb53d4ab4dc652f8dd0ff99da?color=5a5a5a) 3. Schritt:
3. Schritt:  durch Einsetzen in die Tangentengleichung berechnen
durch Einsetzen in die Tangentengleichung berechnen
![\(\begin{array}[t]{rll}
5&=& \dfrac{27}{5}\cdot 5+b&\quad \scriptsize \mid\; - \dfrac{27}{5}\cdot 5\\[5pt]
b&=& 5 -\dfrac{27}{5}\cdot 5&\quad \scriptsize \\[5pt]
b&=& -22
\end{array}\)](https://mathjax.schullv.de/ef77c901b02e8d3ce17b804a7d9071e66d8b8084edf7e03e8a74ba787548b2f0?color=5a5a5a) Die Gleichung der Tangente lautet also
Die Gleichung der Tangente lautet also 
(2)
d)
(1)
Da additive Konstanten beim Ableiten wegfallen, gilt  Die Graphen von
Die Graphen von  und
und  sind daher identisch.
sind daher identisch.
(2)
Wenn der Graph von  genau drei Schnittpunkte mit der
genau drei Schnittpunkte mit der  -Achse besitzen soll, dann dürfen für
-Achse besitzen soll, dann dürfen für  nur Werte eingesetzt werden, die größer als
nur Werte eingesetzt werden, die größer als  und kleiner als
und kleiner als  sind.
sind.
e)
Ein Vergleich mit dem Graphen von  zeigt, dass der Graph von
zeigt, dass der Graph von  um
um  Einheiten nach rechts und um
Einheiten nach rechts und um  Einheiten nach unten verschoben ist.
Es gilt also
Einheiten nach unten verschoben ist.
Es gilt also  und
und 
Aufgabe 4
a)
(1)
Der Punkt  befindet sich an der Stelle
befindet sich an der Stelle 
 Der Punkt
Der Punkt  liegt auf einer Höhe von 2,12 m über dem Niveau des umgebenden Geländes.
liegt auf einer Höhe von 2,12 m über dem Niveau des umgebenden Geländes.
(2)
(3)
Die durchschnittliche Steigung ergibt sich nur aus den Koordinaten zweier Punkte. Über den Verlauf des Abschnitts zwischen diesen Punkten, beispielsweise über das steilste Gefälle im Abschnitt, kann daraus keine Aussage abgeleitet werden.
(4)
1. Schritt:  angeben
angeben
 2. Schritt:
2. Schritt:  mit der angegebenen Steigung gleichsetzen
Zum Weiterrechnen wird nur
mit der angegebenen Steigung gleichsetzen
Zum Weiterrechnen wird nur  genutzt, da sich
genutzt, da sich  nicht im Modellierungsbereich befindet.
3. Schritt:
nicht im Modellierungsbereich befindet.
3. Schritt:  -Koordinate des Punkts berechnen
-Koordinate des Punkts berechnen
 Der Punkt des seitlichen Profils, in dem die durchschnittliche Steigung als Steigung vorkommt, hat ungefähr die Koordinaten
Der Punkt des seitlichen Profils, in dem die durchschnittliche Steigung als Steigung vorkommt, hat ungefähr die Koordinaten 
b)
1. Schritt: Lokale Extremstellen berechnen
 setzen:
Zum Weiterrechnen wird nur
setzen:
Zum Weiterrechnen wird nur  genutzt, da sich
genutzt, da sich  nicht im Modellierungsbereich befindet.
2. Schritt: Das Vorzeichenwechsel-Kriterium anwenden
nicht im Modellierungsbereich befindet.
2. Schritt: Das Vorzeichenwechsel-Kriterium anwenden
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/5d5eecc9fea26eccec45ac8216793d78bc4a149ec0fda6c3b75c449db3109974?color=5a5a5a) An der Stelle
An der Stelle  liegt also ein Vorzeichenwechsel von negativen zu positiven Funktionswerten von
liegt also ein Vorzeichenwechsel von negativen zu positiven Funktionswerten von  und damit ein lokales Minimum von
und damit ein lokales Minimum von  vor.
3. Schritt:
vor.
3. Schritt:  berechnen
berechnen
 Wegen
Wegen 
 und
und  liegt bei
liegt bei  auch das absolute Minimum von
auch das absolute Minimum von  im Intervall
im Intervall ![\([0;8]\)](https://mathjax.schullv.de/f865209a1807ce5fbc790d415dc19a6fa37135ca31f3a6fa1f42441652d095e7?color=5a5a5a) vor.
Daher liegt der niedrigste Punkt des Pumptrack-Abschnitts ca.
vor.
Daher liegt der niedrigste Punkt des Pumptrack-Abschnitts ca.  unterhalb des Niveaus des umgebenden Geländes.
unterhalb des Niveaus des umgebenden Geländes.
c)
(1)
(2)
Die Punkte, die für die horizontale Länge des zweiten Abschnitts gebraucht werden, sind die Nullstellen der Funktion  und können durch Lösen der Gleichung
und können durch Lösen der Gleichung  berechnet werden.
Der solve-Befehl des CAS liefert
berechnet werden.
Der solve-Befehl des CAS liefert  und
und  Der zweite Abschnitt hat also eine horizontale Länge von
Der zweite Abschnitt hat also eine horizontale Länge von 