Prüfungsteil B: Mit Hilfsmitteln
Aufgabe 3
Gegeben ist die Funktion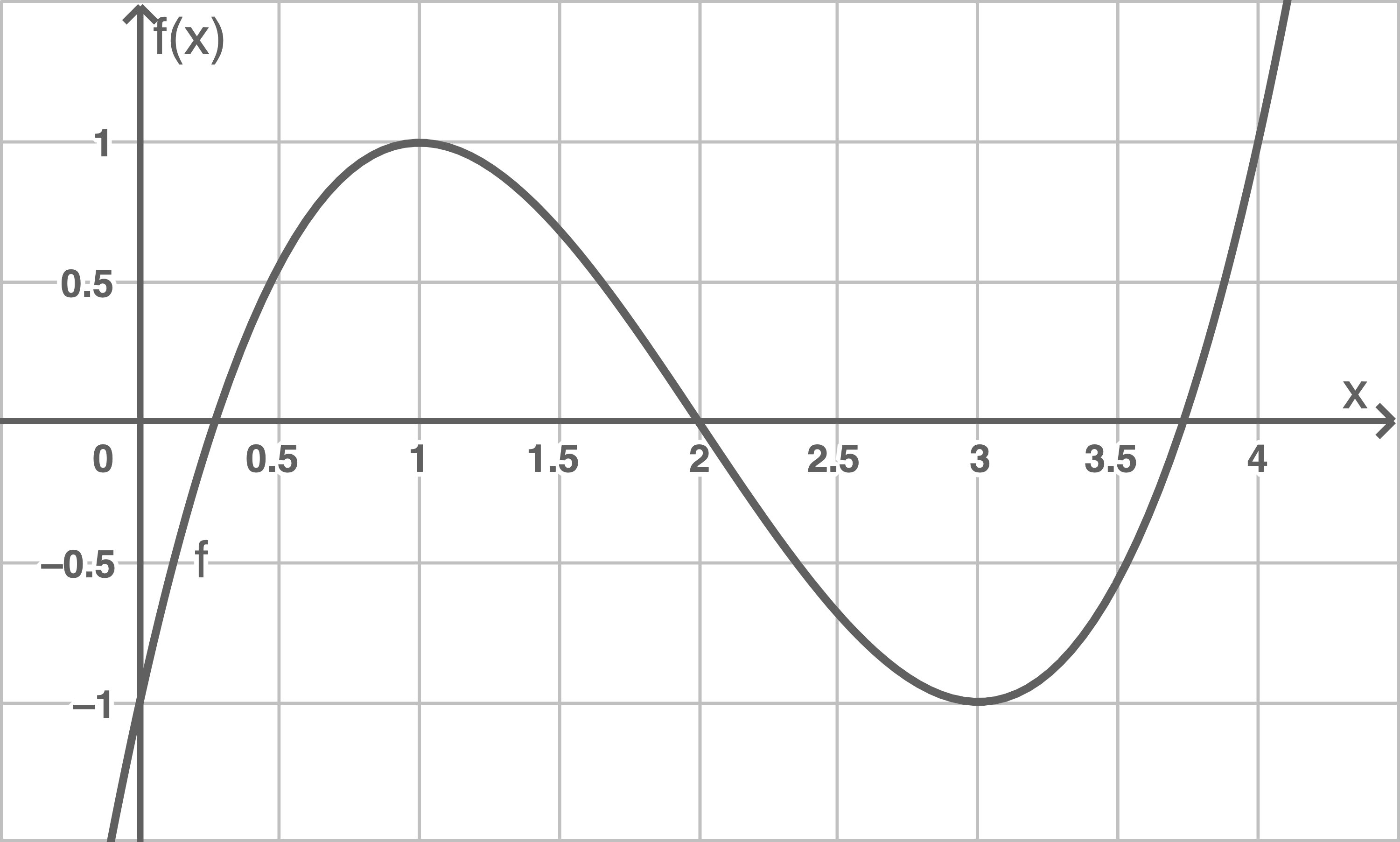
Abbildung 1
a)
Die Funktion  besitzt neben der in der Abbildung 1 ablesbaren Nullstelle
besitzt neben der in der Abbildung 1 ablesbaren Nullstelle  zwei weitere Nullstellen.
Berechne diese und gib die Ergebnisse auf zwei Nachkommastellen gerundet an.
zwei weitere Nullstellen.
Berechne diese und gib die Ergebnisse auf zwei Nachkommastellen gerundet an.
(2 Punkte)
b)
Gib  an und bestimme rechnerisch - ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden - die Koordinaten der lokalen Extrempunkte des Graphen von
an und bestimme rechnerisch - ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden - die Koordinaten der lokalen Extrempunkte des Graphen von 
(7 Punkte)
c)
Für die gegebene Funktion  gilt die folgende Aussage:
Die Anzahl der lokalen Extremstellen ist um eins geringer als die Anzahl der Nullstellen.
Entscheide, ob diese Aussage für alle ganzrationalen Funktionen dritten Grades gilt, und begründe deine Entscheidung.
gilt die folgende Aussage:
Die Anzahl der lokalen Extremstellen ist um eins geringer als die Anzahl der Nullstellen.
Entscheide, ob diese Aussage für alle ganzrationalen Funktionen dritten Grades gilt, und begründe deine Entscheidung.
(3 Punkte)
d)
(1)
Ermittle rechnerisch eine Gleichung der Geraden  die durch die Punkte
die durch die Punkte  und
und  verläuft.
[Zur Kontrolle:
verläuft.
[Zur Kontrolle:  ]
]
(2)
Die Gerade  schneidet den Graphen von
schneidet den Graphen von  in einem weiteren Punkt
in einem weiteren Punkt  Bestimme die Koordinaten von
Bestimme die Koordinaten von 
(3)
Es gibt Stellen, an denen der Graph von  Tangenten hat, die parallel zur Geraden
Tangenten hat, die parallel zur Geraden  verlaufen.
Berechne diese Stellen und gib die Ergebnisse auf zwei Nachkommastellen gerundet an.
verlaufen.
Berechne diese Stellen und gib die Ergebnisse auf zwei Nachkommastellen gerundet an.
(3+2+2 Punkte)
e)
In den folgenden Abbildungen 2.1 bis 2.3 sind für verschiedene Werte von  die zugehörigen Differenzenquotienten
die zugehörigen Differenzenquotienten  veranschaulicht.
veranschaulicht.
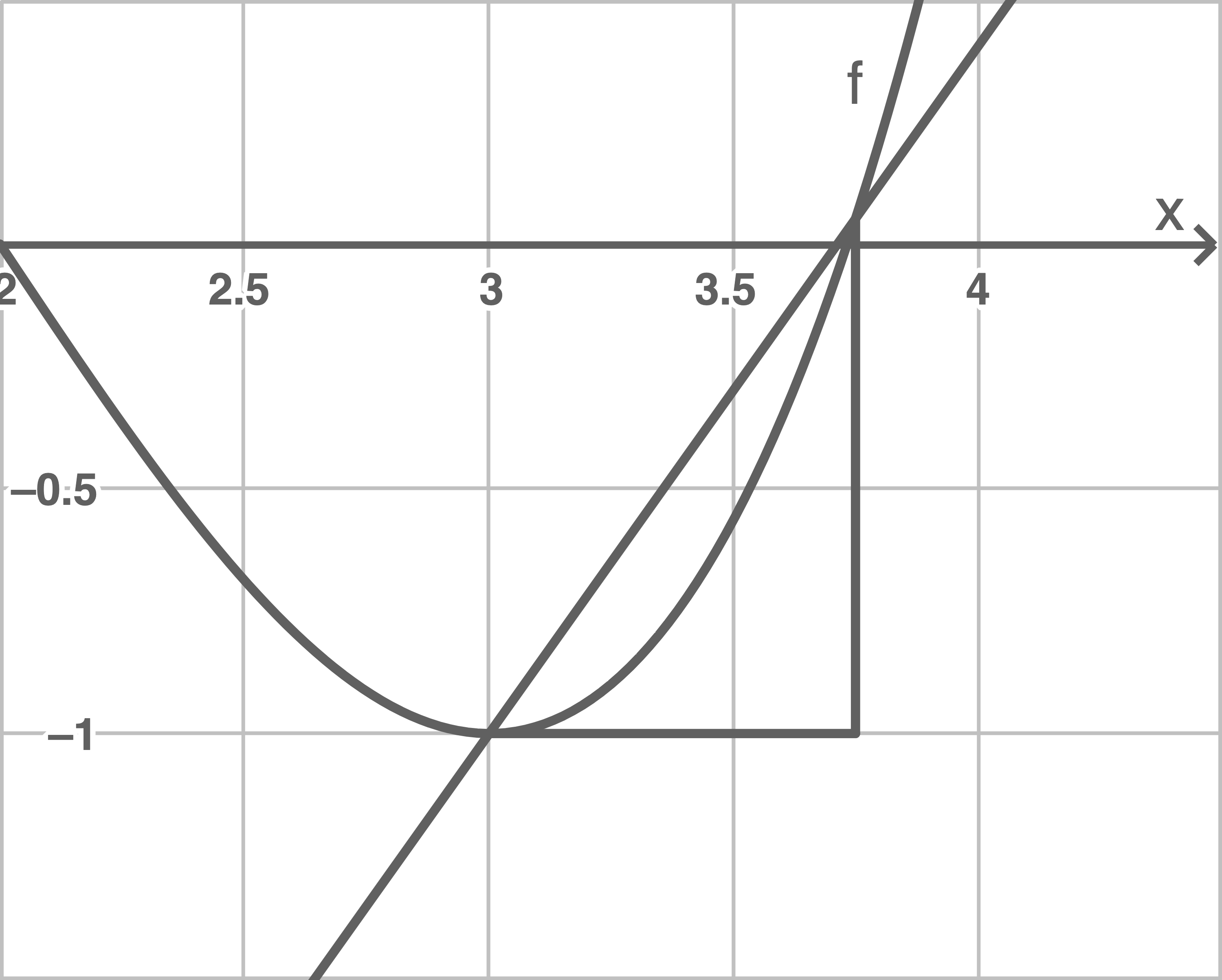
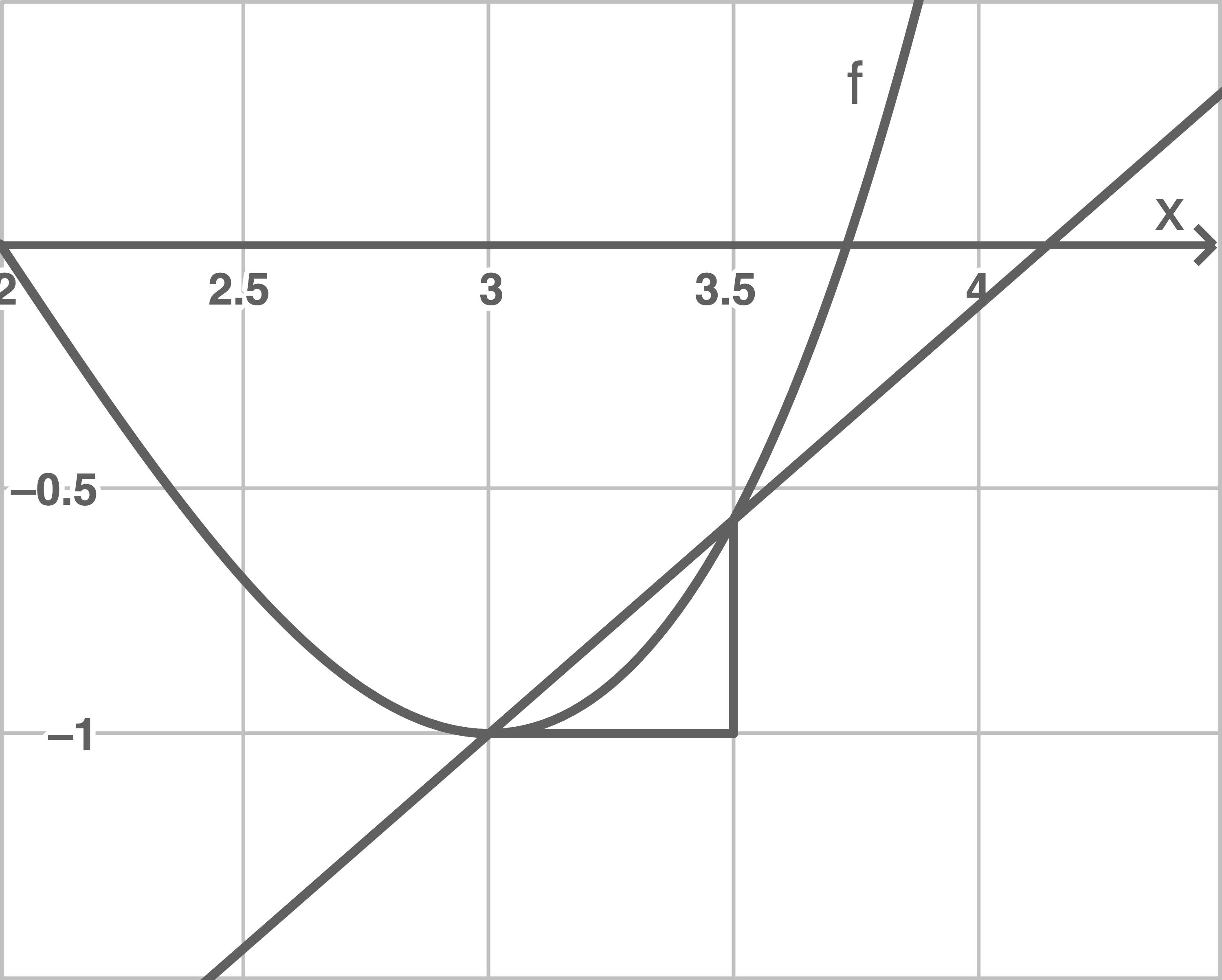


Abbildung 2.1

Abbildung 2.2

Abbildung 2.3
(1)
Entscheide, welche der Abbildungen 2.1 oder 2.3 zu dem Wert  gehört.
gehört.
(2)
Gib an, welcher Wert von  zu der Abbildung 2.2 gehört.
zu der Abbildung 2.2 gehört.
(3)
Wenn  immer kleiner wird, dann nähert sich der Wert des Differenzenquotienten
immer kleiner wird, dann nähert sich der Wert des Differenzenquotienten  einer bestimmten Zahl an.
Gib diese Zahl an und begründe deine Angabe.
einer bestimmten Zahl an.
Gib diese Zahl an und begründe deine Angabe.
(1+1+3 Punkte)
Aufgabe 4
Der Ederstausee in Hessen ist einer der größten Stauseen in Deutschland. Wenn er bis zum Überlauf gefüllt ist (Vollstau), dann enthält er eine Wassermenge von 200 Millionen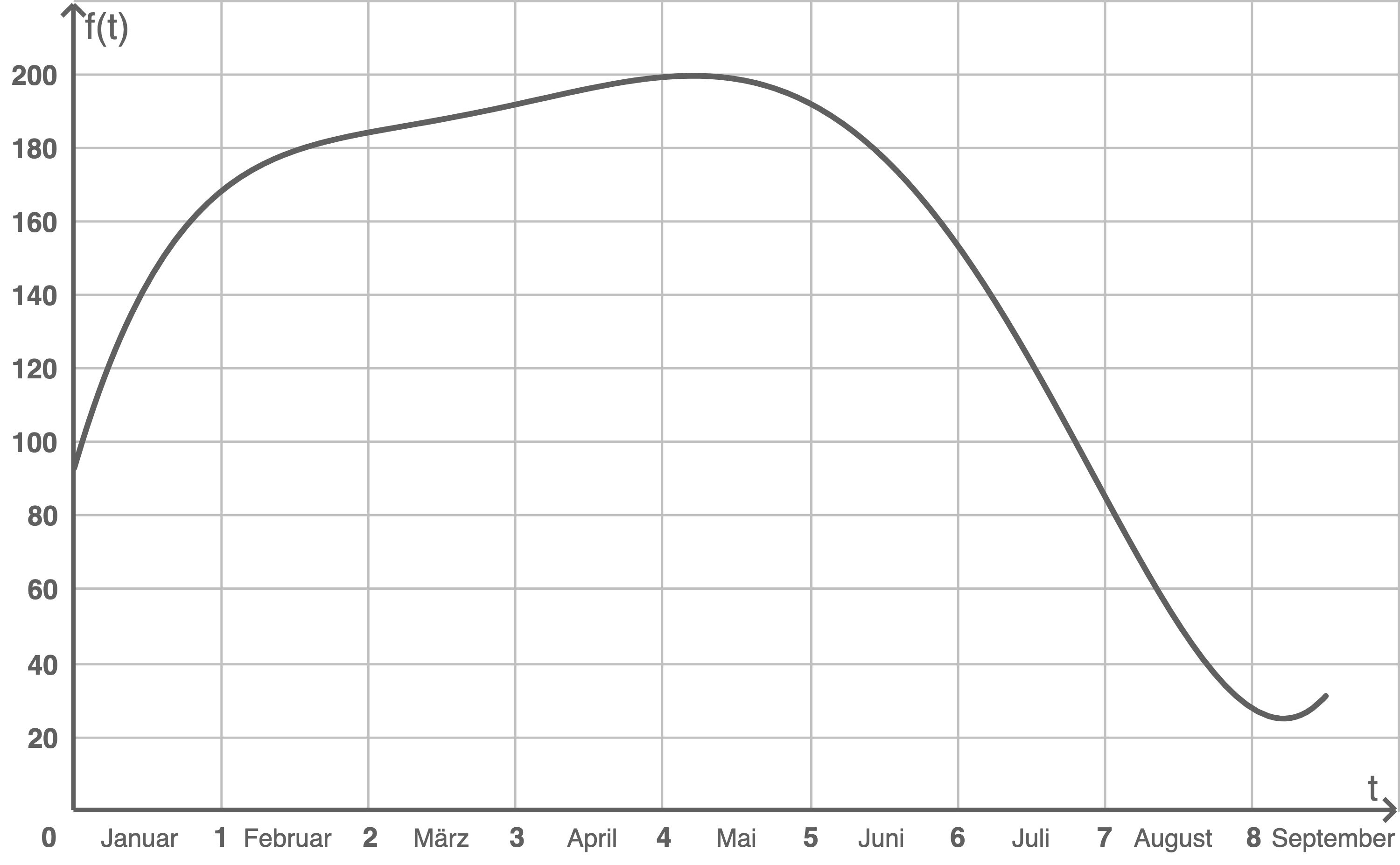
Abbildung 3
a)
Berechne die Füllmenge des Ederstausees am 01. April 2022.
(2 Punkte)
b)
Bei der Entstehung des Ederstausees vor mehr als 100 Jahren wurden Bauwerke überflutet. Einige davon werden bei Niedrigwasser wieder sichtbar, das „Edersee-Atlantis“. Das am besten erhaltene Bauwerk ist die Aseler Brücke.
 Die Aseler Brücke ist begehbar, wenn der Ederstausee nur noch
Die Aseler Brücke ist begehbar, wenn der Ederstausee nur noch  der Füllmenge enthält, die bei Vollstau vorliegt.
Bestimme, ab wann die Aseler Brücke im Jahr 2022 begehbar war.
[Hinweis: Die Angabe eines exakten Datums ist nicht erforderlich.]
der Füllmenge enthält, die bei Vollstau vorliegt.
Bestimme, ab wann die Aseler Brücke im Jahr 2022 begehbar war.
[Hinweis: Die Angabe eines exakten Datums ist nicht erforderlich.]

Abbildung 4: Aseler Brücke bei Niedrigwasser des Ederstausees
(4 Punkte)
c)
Berechne  und deute das Ergebnis im Sachzusammenhang.
und deute das Ergebnis im Sachzusammenhang.
(4 Punkte)
d)
Gib  an und bestimme rechnerisch - ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden - die geringste Füllmenge des Ederstausees im Zeitraum von Anfang Januar 2022 bis Mitte September 2022.
an und bestimme rechnerisch - ohne dabei an Funktionsgraphen abgelesene Werte oder Zusammenhänge zu verwenden - die geringste Füllmenge des Ederstausees im Zeitraum von Anfang Januar 2022 bis Mitte September 2022.
In der Abbildung 5 ist neben dem Graphen von
(8 Punkte)
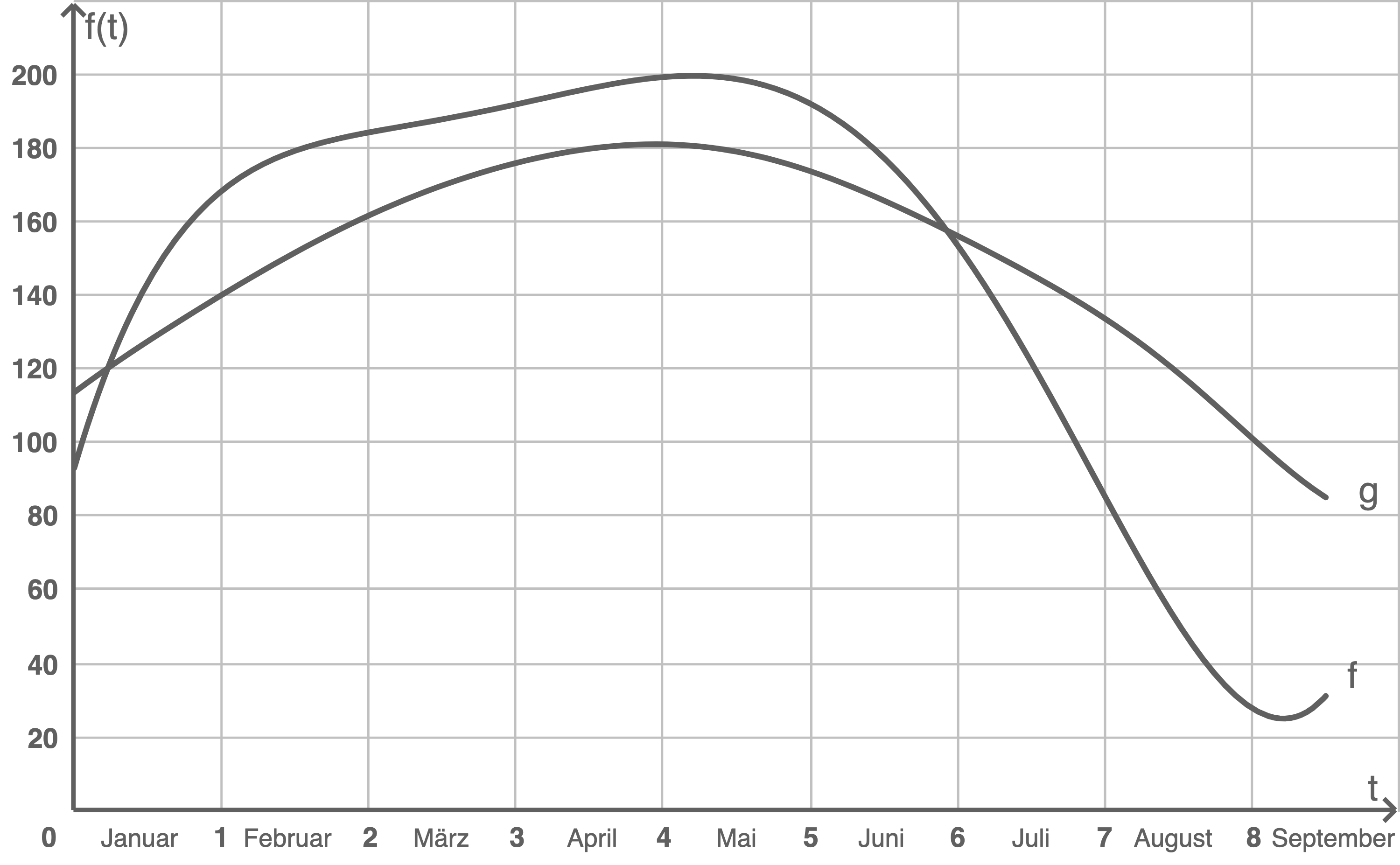
Abbildung 5
e)
(1)
Gib für  näherungsweise die Bereiche an, in denen
näherungsweise die Bereiche an, in denen  gilt, und interpretiere die Bedeutung dieser Bereiche im Sachzusammenhang.
gilt, und interpretiere die Bedeutung dieser Bereiche im Sachzusammenhang.
(2)
Für  liegt der größte vertikale Abstand (Abstand in
liegt der größte vertikale Abstand (Abstand in  -Richtung) der Graphen von
-Richtung) der Graphen von  und
und  im Bereich
im Bereich  vor.
Ermittle näherungsweise diesen Abstand und interpretiere den ermittelten Wert im Sachzusammenhang.
vor.
Ermittle näherungsweise diesen Abstand und interpretiere den ermittelten Wert im Sachzusammenhang.
(3+3 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 3
a)
b)
c)
Die Aussage gilt nicht für alle ganzrationalen Funktionen dritten Grades. Verschiebt man beispielsweise den Graphen der Funktion  um zwei Einheiten in positive
um zwei Einheiten in positive  -Richtung, so hat die zugehörige Funktion dritten Grades nur noch eine Nullstelle, aber weiterhin zwei lokale Extremstellen.
-Richtung, so hat die zugehörige Funktion dritten Grades nur noch eine Nullstelle, aber weiterhin zwei lokale Extremstellen.
d)
(1)
Die allgemeine Geradengleichung lautet  Die Steigung
Die Steigung  lässt sich über den Differenzenquotienten berechnen:
lässt sich über den Differenzenquotienten berechnen:
 Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  liefert:
liefert:
![\(\begin{array}[t]{rll}
f(x) &=& -1\cdot x+c \\[5pt]
1 &=& -1\cdot 1+c \quad \scriptsize \mid\;+1 \\[5pt]
2 &=& c
\end{array}\)](https://mathjax.schullv.de/9ced5474695bb2d328c441f52e7e45a6e308fcb2cc882d4aab1471dd1b7da0a0?color=5a5a5a) Die gesuchte Geradengleichung lautet
Die gesuchte Geradengleichung lautet 
(2)
(3)
An den gesuchten Stellen muss der Graph von  die gleiche Steigung wie die Gerade haben. Es muss also
die gleiche Steigung wie die Gerade haben. Es muss also  gelten.
Der solve-Befehl des CAS liefert
gelten.
Der solve-Befehl des CAS liefert  und
und 
e)
(1)
Zu  gehört die Abbildung 2.3.
gehört die Abbildung 2.3.
(2)
Zu Abbildung 2.2 gehört der Wert 
(3)
Der Differenzenquotient nähert sich für kleine  der Ableitung von
der Ableitung von  an der Stelle
an der Stelle  an. An der Stelle
an. An der Stelle  besitzt der Graph von
besitzt der Graph von  einen Tiefpunkt, weshalb die Ableitung an dieser Stelle gleich null ist.
Der gegebene Differenzenquotient nähert sich für kleine
einen Tiefpunkt, weshalb die Ableitung an dieser Stelle gleich null ist.
Der gegebene Differenzenquotient nähert sich für kleine  also der Zahl
also der Zahl  an.
an.
Lösung 4
a)
b)
Bei Vollstau enthält der Ederstausee eine Wassermenge von  Millionen
Millionen 
 Gesucht ist die Lösung der Gleichung
Gesucht ist die Lösung der Gleichung  Der solve-Befehl des CAS liefert
Der solve-Befehl des CAS liefert  Die anderen beiden Lösungen liegen nicht im betrachteten Bereich von
Die anderen beiden Lösungen liegen nicht im betrachteten Bereich von  Die Brücke war also ungefähr ab August wieder begehbar.
Die Brücke war also ungefähr ab August wieder begehbar.
c)
d)
Die geringste Füllmenge entspricht dem globalen Minimum der Funktion  im Bereich
im Bereich 
 Der solve-Befehl des CAS liefert
Der solve-Befehl des CAS liefert  und
und 

 An der Stelle
An der Stelle  liegt ein Vorzeichenwechsel von
liegt ein Vorzeichenwechsel von  nach
nach  vor, also ein Maximum von
vor, also ein Maximum von 

 An der Stelle
An der Stelle  liegt ein Vorzeichenwechsel von
liegt ein Vorzeichenwechsel von  nach
nach  und damit ein lokales Minimum von
und damit ein lokales Minimum von  Es müssen noch die Intervallränder überprüft werden:
Es müssen noch die Intervallränder überprüft werden:


 Die geringste Füllmenge des Ederstausees betrug ca.
Die geringste Füllmenge des Ederstausees betrug ca.  Millionen
Millionen 
e)
(1)
Ungefähr für  und
und  gilt
gilt  In diesen Bereichen war im Jahr 2022 weniger Wasser im Ederstausee als im Durchschnitt in den letzen dreißig Jahren.
In diesen Bereichen war im Jahr 2022 weniger Wasser im Ederstausee als im Durchschnitt in den letzen dreißig Jahren.
(2)
Der Abbildung kann entnommen werden, dass der Abstand ca.  beträgt.
Im Sachzusammenhang bedeutet das, dass Anfang September ungefähr
beträgt.
Im Sachzusammenhang bedeutet das, dass Anfang September ungefähr  Millionen
Millionen  Wasser weniger im Stausee waren als die letzten
Wasser weniger im Stausee waren als die letzten  Jahre im Durchschnitt. Das entspricht der größten Differenz im Zeitraum von Januar bis Mitte September.
Jahre im Durchschnitt. Das entspricht der größten Differenz im Zeitraum von Januar bis Mitte September.