Prüfungsteil B: Mit Hilfsmitteln
Aufgabe 3:
Gegeben ist die Funktion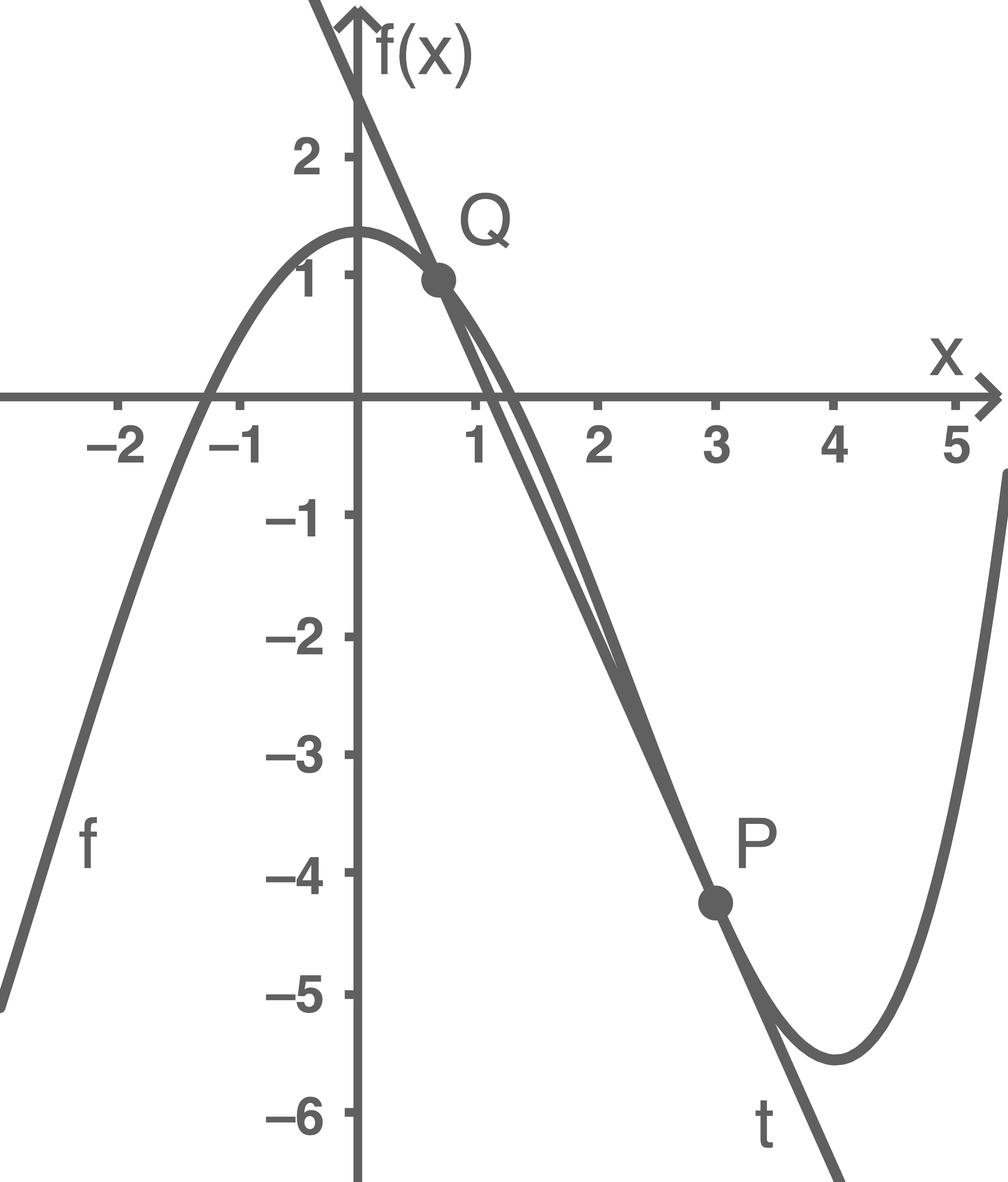
Abbildung
a)
(1)
Ermittle rechnerisch eine Gleichung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  .
[Kontrollergebnis:
.
[Kontrollergebnis:  ]
]
(2)
In der Abbildung ist ein weiterer gemeinsamer Punkt  des Graphen von
des Graphen von  und der Tangente
und der Tangente  eingezeichnet.
Ermittle die Koordinaten von
eingezeichnet.
Ermittle die Koordinaten von  .
.
(3)
Der Koordinatenursprung und die Schnittpunkte der Tangente  mit den Koordinatenachsen sind die Eckpunkte eines Dreiecks.
Berechne den Flächeninhalt
mit den Koordinatenachsen sind die Eckpunkte eines Dreiecks.
Berechne den Flächeninhalt  dieses Dreiecks.
dieses Dreiecks.
(4 + 3 + 4 Punkte)
b)
(1)
Bestimme rechnerisch alle lokalen Extremstellen von 
(2)
Weise nach, dass der lokale Hochpunkt  kein globaler Hochpunkt des Graphen von
kein globaler Hochpunkt des Graphen von  ist.
ist.
(3)
Der Definitionsbereich von  wird jetzt auf das Intervall von
wird jetzt auf das Intervall von  bis
bis  eingeschränkt. Wählt man beispielsweise
eingeschränkt. Wählt man beispielsweise  , so ist der lokale Hochpunkt
, so ist der lokale Hochpunkt  auch der globale Hochpunkt des Graphen von
auch der globale Hochpunkt des Graphen von  Gesucht ist nun die größte Zahl
Gesucht ist nun die größte Zahl  mit den beiden folgenden Eigenschaften:
mit den beiden folgenden Eigenschaften:
 .
.
- Im Intervall von
bis
ist der lokale Hochpunkt
auch der globale Hochpunkt des Graphen von
.
besitzt genau eine Nachkommastelle.
(8 + 2 + 3 Punkte)
Aufgabe 4:
Seit einigen Jahren wird verstärkt über die Feinstaubbelastung in Städten diskutiert. An einer Messstation in einer Stadt wurde über einen längeren Zeitraum die Feinstaubkonzentration1 aufgezeichnet. Zur Modellierung der gemessenen Feinstaubkonzentration im Verlauf eines Tages zwischen 0:00 Uhr und 12:00 Uhr wird für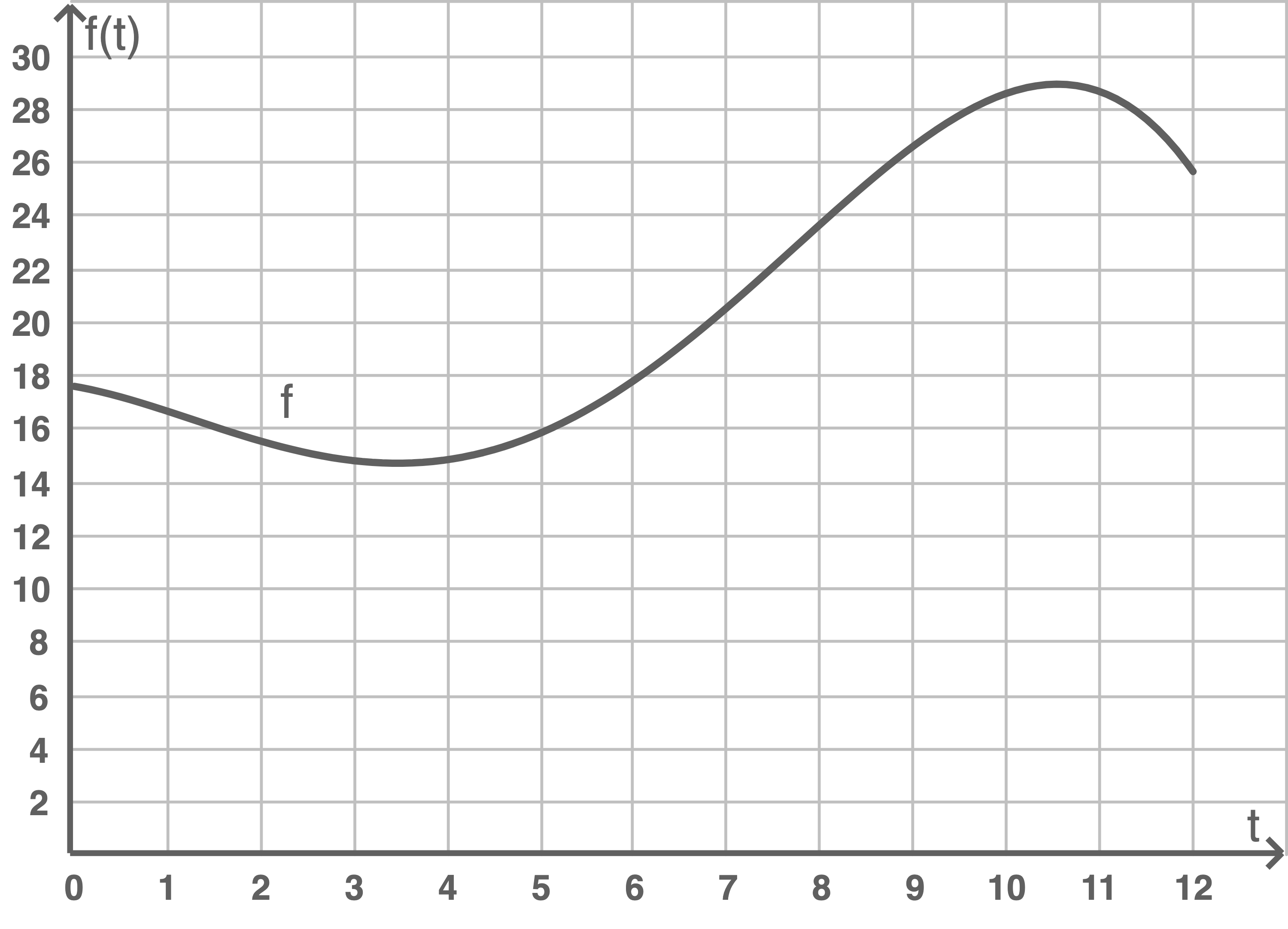
Abbildung 1
a)
Ermittle, um wie viel  die Feinstaubkonzentration zwischen 6:00 Uhr und 10:00 Uhr zunimmt.
die Feinstaubkonzentration zwischen 6:00 Uhr und 10:00 Uhr zunimmt.
(3 Punkte)
b)
Ermittle rechnerisch die maximale und die minimale Feinstaubkonzentration im Zeitraum von 0:00 Uhr bis 12:00 Uhr.
[Kontrolllösung: Die maximale Feinstaubkonzentration beträgt ca.  .]
.]
(8 Punkte)
c)
Der Stadtrat fordert, dass ein Wert von  nicht überschritten werden soll.
nicht überschritten werden soll.
(1)
Berechne, um wie viel Prozent die in b) ermittelte maximale Feinstaubkonzentration den Wert von  überschreitet.
überschreitet.
(2)
Bestimme rechnerisch, wie lange der Wert von  im Zeitraum von 0:00 Uhr bis 12:00 Uhr überschritten wird.
im Zeitraum von 0:00 Uhr bis 12:00 Uhr überschritten wird.
(3 + 4 Punkte)
d)
Im Stadtrat werden verschiedene Maßnahmenpakete zur Verringerung der Feinstaubkonzentration diskutiert:
 (Maßnahmenpaket A) und
(Maßnahmenpaket A) und  (Maßnahmenpaket B) modelliert. Die Funktionen
(Maßnahmenpaket B) modelliert. Die Funktionen  und
und  gehen jeweils durch eine Transformation aus der Funktion
gehen jeweils durch eine Transformation aus der Funktion  hervor. Die Graphen von
hervor. Die Graphen von  und
und  sind in Abbildung 2 dargestellt.
sind in Abbildung 2 dargestellt.
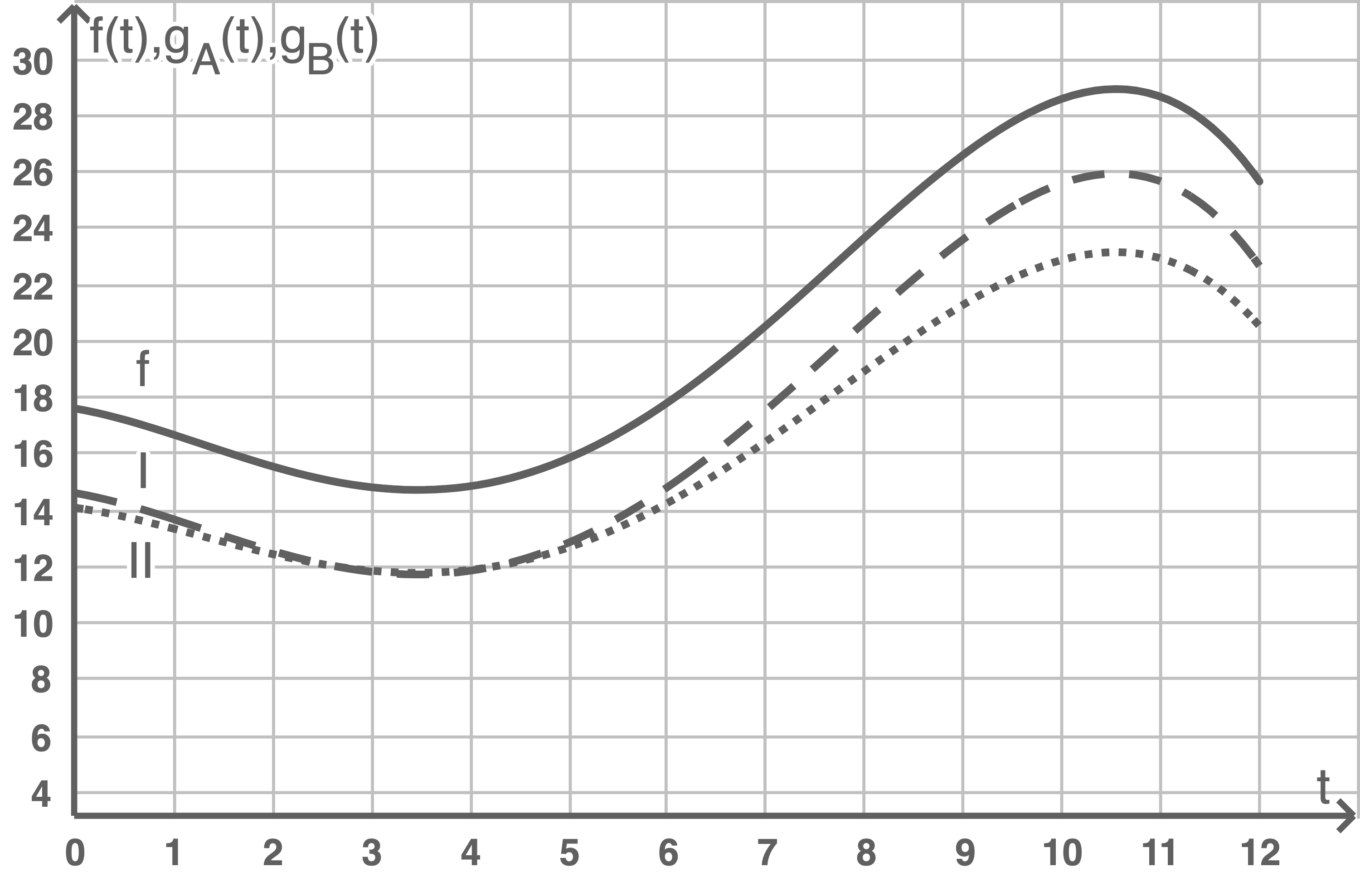
- Maßnahmenpaket A soll die Feinstaubkonzentration zu jeder Tageszeit im Vergleich zu der bisher durch
modellierten Feinstaubkonzentration um
verringern.
- Maßnahmenpaket B soll die Feinstaubkonzentration zu jeder Tageszeit im Vergleich zu der bisher durch
modellierten Feinstaubkonzentration um
verringern.

Abbildung 2
(1)
Gib begründet an, welcher der Funktionsgraphen zur Funktion  und welcher zur Funktion
und welcher zur Funktion  gehört.
gehört.
(2)
Gib für die Funktionen  und
und  jeweils eine Funktionsgleichung an.
jeweils eine Funktionsgleichung an.
(3 + 3 Punkte)
[1] Feinstaub wird, abhängig von der Partikelgröße, in die drei Klassen PM 10, PM 2,5 und Ultrafeinstaub eingeteilt. In der folgenden Aufgabe wird die Konzentration von Feinstaub der Klasse PM 10 modelliert.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 3
a)
(1)
Der Ansatz für die Gleichung einer Tangente lautet
 1. Steigung der Tangente mit der 1. Ableitung berechnen
1. Steigung der Tangente mit der 1. Ableitung berechnen



 2. Koordinaten einsetzen
2. Koordinaten einsetzen
![\(\begin{array}[t]{rll}
t: \, y &=& -\dfrac{9}{4} \cdot x + b_t \quad \scriptsize \mid\; P\left(3 \mid -\dfrac{17}{4}\right) \\[5pt]
-\dfrac{17}{4} &=& -\dfrac{9}{4} \cdot 3 + b_t \\[5pt]
-\dfrac{17}{4} &=& -\dfrac{27}{4} + b_t \quad \scriptsize \mid\;+\frac{27}{4} \\[5pt]
\dfrac{5}{2} &=& b_t \\[5pt]
\end{array}\)](https://mathjax.schullv.de/2bcd63b82ed51490497943e710276fe7655e2a62793f4652b8e9fcc6ab57f752?color=5a5a5a) Eine Gleichung der Tangente
Eine Gleichung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  lautet:
lautet:

(2)
Mit dem solve-Befehl des CAS lässt sich die Gleichung  lösen und anschließend die zugehörigen
lösen und anschließend die zugehörigen  -Koordinaten berechnen.
Es ergeben sich
-Koordinaten berechnen.
Es ergeben sich 
 und
und  Da der erste Punkt im negativen Bereich liegt und es sich bei dem zweiten Punkt um
Da der erste Punkt im negativen Bereich liegt und es sich bei dem zweiten Punkt um  handelt, lauten die Koordinaten von
handelt, lauten die Koordinaten von  ungefähr
ungefähr 
(3)
Für den Flächeninhalt eines Dreiecks gilt:
 Da zwei der Seiten des Dreiecks auf den Koordinatenachsen liegen, befindet sich im Koordinatenursprung ein rechter Winkel.
Daher wird die Länge der Grundseite
Da zwei der Seiten des Dreiecks auf den Koordinatenachsen liegen, befindet sich im Koordinatenursprung ein rechter Winkel.
Daher wird die Länge der Grundseite  durch die Schnittstelle der Geraden
durch die Schnittstelle der Geraden  mit der
mit der  -Achse definiert:
-Achse definiert:
![\(\begin{array}[t]{rll}
0 &=& -\dfrac{9}{4} \cdot x + \dfrac{5}{2} \quad \scriptsize \mid\;+\dfrac{9}{4} \cdot x\\[5pt]
\dfrac{9}{4} \cdot x &=& \dfrac{5}{2} \quad \scriptsize \mid\; \cdot \dfrac{4}{9} \\[5pt]
x &=& \dfrac{10}{9}
\end{array}\)](https://mathjax.schullv.de/85d7f7a87540e7b01d6569914fd7fb7bff06820222082f48dfd57665aa9ce373?color=5a5a5a) Es gilt also
Es gilt also  Analog dazu ist
Analog dazu ist  durch den
durch den  -Achsenabschnitt der Geraden
-Achsenabschnitt der Geraden  gegeben:
gegeben:  Für den Flächeninhalt folgt:
Für den Flächeninhalt folgt:
 Der Flächeninhalt
Der Flächeninhalt  des Dreiecks beträgt
des Dreiecks beträgt  Flächeneinheiten.
Flächeneinheiten.
b)
(1)
1. Notwendiges Kriterium für lokale Extremstellen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/c793ad2069f3a48840591edf719390906556124802811c2100e2069fe11c58bf?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  wenn
wenn  oder
oder  gilt. Mit der
gilt. Mit der  -Formel ergibt sich:
2. Vorzeichenwechselkriterium überprüfen
-Formel ergibt sich:
2. Vorzeichenwechselkriterium überprüfen
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/dfe3b40e4ad79d12acafceac51e013351f8a7732d75946359835d11074eb164d?color=5a5a5a) An den Stellen
An den Stellen  und
und  liegt ein Vorzeichenwechsel von negativ zu positiv vor, sodass es sich bei diesen beiden Stellen um lokale Minimalstellen von
liegt ein Vorzeichenwechsel von negativ zu positiv vor, sodass es sich bei diesen beiden Stellen um lokale Minimalstellen von  handelt.
handelt.
An der Stelle liegt ein Vorzeichenwechsel von positiv zu negativ vor, sodass es sich bei
liegt ein Vorzeichenwechsel von positiv zu negativ vor, sodass es sich bei  um eine Maximalstelle von
um eine Maximalstelle von  handelt.
handelt.
An der Stelle
(2)
Es gilt beispielsweise:
 Da
Da  gilt, ist
gilt, ist  kein globaler Hochpunkt des Graphen von
kein globaler Hochpunkt des Graphen von 
(3)
Die erste Bedingung ist erfüllt, wenn  gilt. Mit dem CAS ergeben sich für
gilt. Mit dem CAS ergeben sich für  die Lösungen
die Lösungen 
 und
und  Da
Da  vorgegeben ist, wird nur
vorgegeben ist, wird nur  betrachtet.
Es gilt:
betrachtet.
Es gilt:  und
und  Also folgt
Also folgt 
Lösung 4
a)
Mit dem CAS können die Funktionswerte von  ermittelt werden:
ermittelt werden:
![\(\begin{array}[t]{rll}
f(6) &\approx& 17,82 \\[5pt]
f(10) &=& 28,6 \\[5pt]
f(10)-f(6) &\approx& 28,6 - 17,82 \\[5pt]
&=& 10, 78
\end{array}\)](https://mathjax.schullv.de/dee221abcd94b600fa0451125bf1e74045854a2c13b427a4c64f1dfe0da224e4?color=5a5a5a) Zwischen 6:00 Uhr und 10:00 Uhr nimmt die Feinstaubkonzentration um ca.
Zwischen 6:00 Uhr und 10:00 Uhr nimmt die Feinstaubkonzentration um ca.  zu.
zu.
b)
1. Notwendige Bedingung für lokale Extremstellen




 Mit dem solve-Befehl des CAS ergeben sich für
Mit dem solve-Befehl des CAS ergeben sich für  die Lösungen
die Lösungen 
 und
und  Es wird das Intervall
Es wird das Intervall ![\([0;12]\)](https://mathjax.schullv.de/5ba9b38204a320e9433651393178f89e741e0a72de8e09a0201574090d0733c6?color=5a5a5a) betrachtet, das
betrachtet, das  nicht beinhaltet. Es werden also nur
nicht beinhaltet. Es werden also nur  und
und  betrachtet.
Alle Stellen, an denen sich das gesuchte Maximum oder Minimum befinden können, sind die Intervallränder und
betrachtet.
Alle Stellen, an denen sich das gesuchte Maximum oder Minimum befinden können, sind die Intervallränder und  und
und  2. Vergleich der Funktionswerte
2. Vergleich der Funktionswerte
![\(\begin{array}[t]{rll}
f(0) &=& 17,6 \\[5pt]
f(3,47) &\approx& 14,72 \\[5pt]
f(10,55) &\approx& 28,94 \\[5pt]
f(12) &\approx& 25,66
\end{array}\)](https://mathjax.schullv.de/efca61e7e330274d8b4107e7e9a92db3484f3e5e60f8dcc309fa71735ae4bb73?color=5a5a5a) Die maximale Feinstaubkonzentration im betrachteten Zeitraum beträgt also ca.
Die maximale Feinstaubkonzentration im betrachteten Zeitraum beträgt also ca.  die minimale ca.
die minimale ca. 
c)
(1)
(2)
d)
(1)
Graph I gehört zur Funktion  Graph II gehört zur Funktion
Graph II gehört zur Funktion  Der Graph der Funktion
Der Graph der Funktion  geht durch eine Verschiebung um 3 LE nach unten aus dem Graphen von
geht durch eine Verschiebung um 3 LE nach unten aus dem Graphen von  hervor. Der vertikale Abstand des Graphen II zum Graphen von
hervor. Der vertikale Abstand des Graphen II zum Graphen von  ist beispielsweise an der Stelle
ist beispielsweise an der Stelle  größer als 4 LE. Damit kann Graph II nicht zur Funktion
größer als 4 LE. Damit kann Graph II nicht zur Funktion  gehören, also gehört Graph I zu
gehören, also gehört Graph I zu  und Graph II zu
und Graph II zu 
(2)