Prüfungsteil B: Mit Hilfsmitteln
Aufgabe 3: Analysis
Gegeben ist die Funktion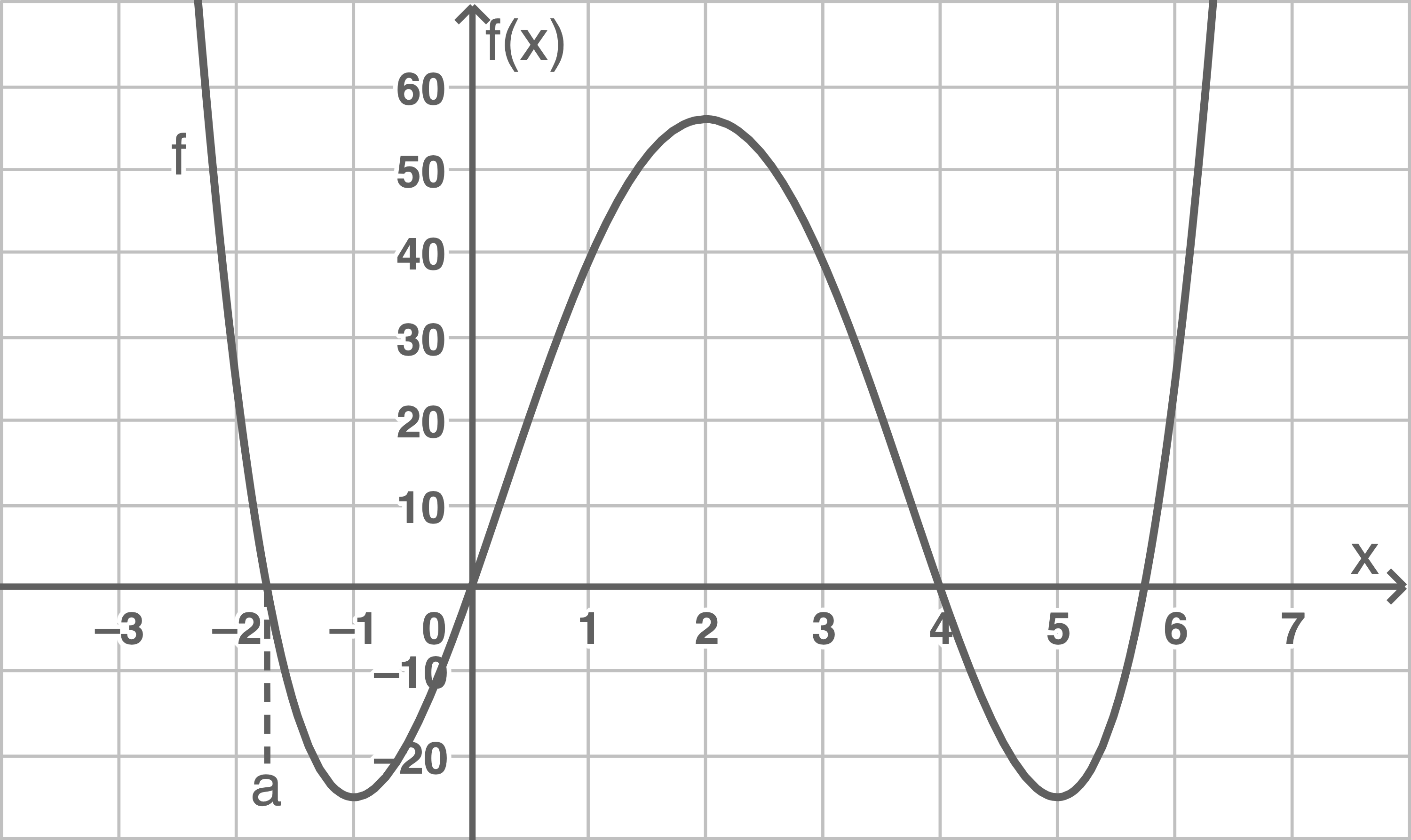
Abbildung
a)
Ermittle die in der Abbildung markierte Nullstelle  auf zwei Nachkommastellen genau.
auf zwei Nachkommastellen genau.
(2 Punkte)
b)
Weise rechnerisch nach, dass  eine lokale Maximalstelle der Funktion
eine lokale Maximalstelle der Funktion  ist.
ist.
(6 Punkte)
c)
(1)
Zeichne die Sekante  durch die Punkte
durch die Punkte  und
und  des Graphen von
des Graphen von  in die Abbildung ein und berechne die Steigung von
in die Abbildung ein und berechne die Steigung von 
(2)
Bestimme rechnerisch eine Gleichung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt 
[Zur Kontrolle: Die Steigung von ist
ist  ]
]
[Zur Kontrolle: Die Steigung von
(3)
Zeichne die Tangente  in die Abbildung ein.
in die Abbildung ein.
(4)
Die Steigung einer Sekante  durch den Punkt
durch den Punkt  und einen weiteren Punkt
und einen weiteren Punkt  des Graphen von
des Graphen von  soll sich um weniger als
soll sich um weniger als  von der Steigung der Tangente
von der Steigung der Tangente  unterscheiden.
unterscheiden.
Ermittle durch systematisches Probieren die Koordinaten eines Punktes so, dass diese Bedingung erfüllt ist.
so, dass diese Bedingung erfüllt ist.
Ermittle durch systematisches Probieren die Koordinaten eines Punktes
(3+4+2+3 Punkte)
d)
Der Graph der Funktion  wird nacheinander folgenden Transformationen unterzogen:
wird nacheinander folgenden Transformationen unterzogen:
 bezeichnet.
bezeichnet.
Gib eine Gleichung von an.
an.
[Hinweis: Eine Vereinfachung der Gleichung von ist nicht erforderlich.]
ist nicht erforderlich.]
- Der Graph wird in Richtung der
-Achse so gestaucht, dass der gestauchte Graph den lokalen Hochpunkt
besitzt.
- Im Anschluss wird der gestauchte Graph um drei Einheiten nach rechts verschoben.
Gib eine Gleichung von
[Hinweis: Eine Vereinfachung der Gleichung von
(4 Punkte)
Aufgabe 4: Analysis
Aufgrund ergiebiger Regenfälle wurde in der zweiten Oktoberhälfte 2016 am Rhein ein Ansteigen des Wassers beobachtet.Am 20.10.2016 um 0:00 Uhr wurde an der Messstelle in Bonn ein Wasserstand[1] von
Eine Schülerin verwendet die auf
Dabei entspricht z.B.
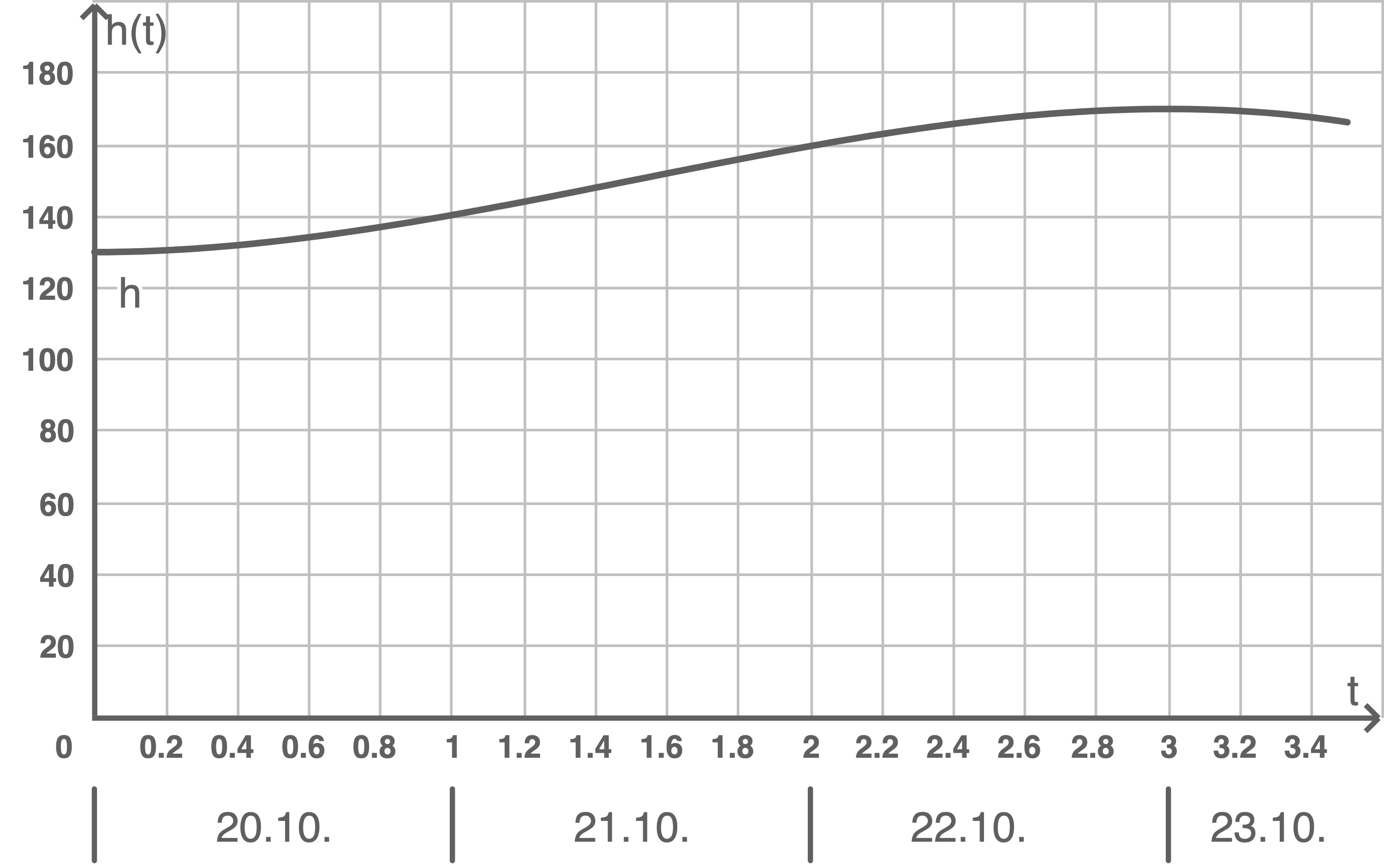
Abbildung 2
a)
Berechne den Wasserstand des Rheins an der Messstelle in Bonn am 21.10.2016 um 12:00 Uhr.
(3 Punkte)
b)
Berechne  und interpretiere den berechneten Wert im Sachzusammenhang.
und interpretiere den berechneten Wert im Sachzusammenhang.
(4 Punkte)
c)
Ermittle rechnerisch den niedrigsten und höchsten Wasserstand im betrachteten Zeitraum.
(9 Punkte)
d)
Bestimme rechnerisch, wie lange der Wasserstand im betrachteten Zeitraum zwischen  und
und  lag.
lag.
In der folgenden Aufgabe e) wird der Wasserstand in einem über den 23.10.2016 hinausgehenden Zeitraum betrachtet.
(4 Punkte)
e)
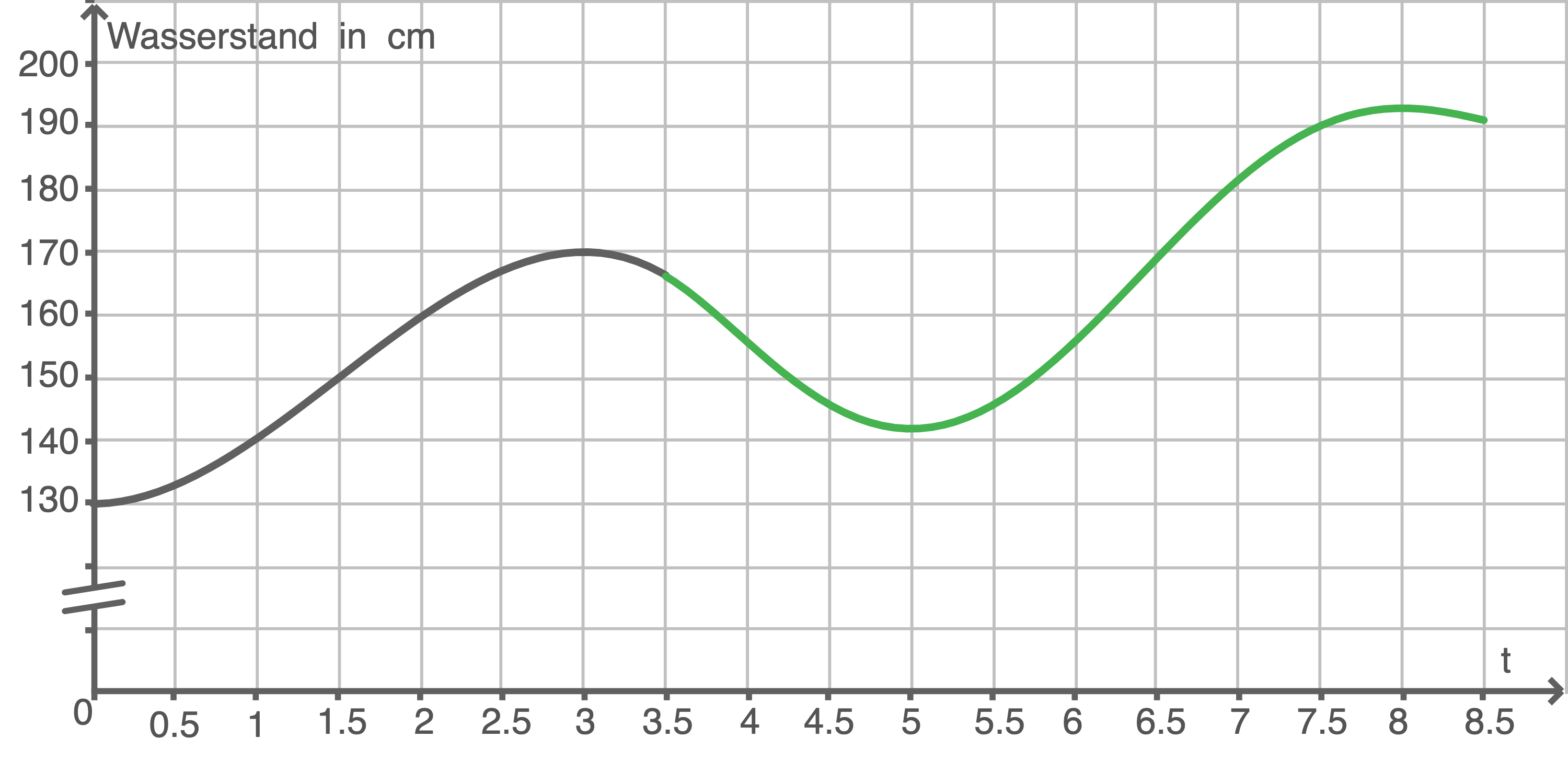
In der folgenden Abbildung 3 ist der Wasserstand im Zeitraum vom 20.10.2016, 0:00 Uhr  bis zum 23.10.2016, 12:00 Uhr
bis zum 23.10.2016, 12:00 Uhr  in einem erweiterten Koordinatensystem dargestellt.
in einem erweiterten Koordinatensystem dargestellt.
Die Abbildung 4 zeigt die momentane Änderungsrate des Wasserstandes im verlängerten Zeitraum vom 20.10.2016, 0:00 Uhr, bis zum 28.10.2016, 12:00 Uhr
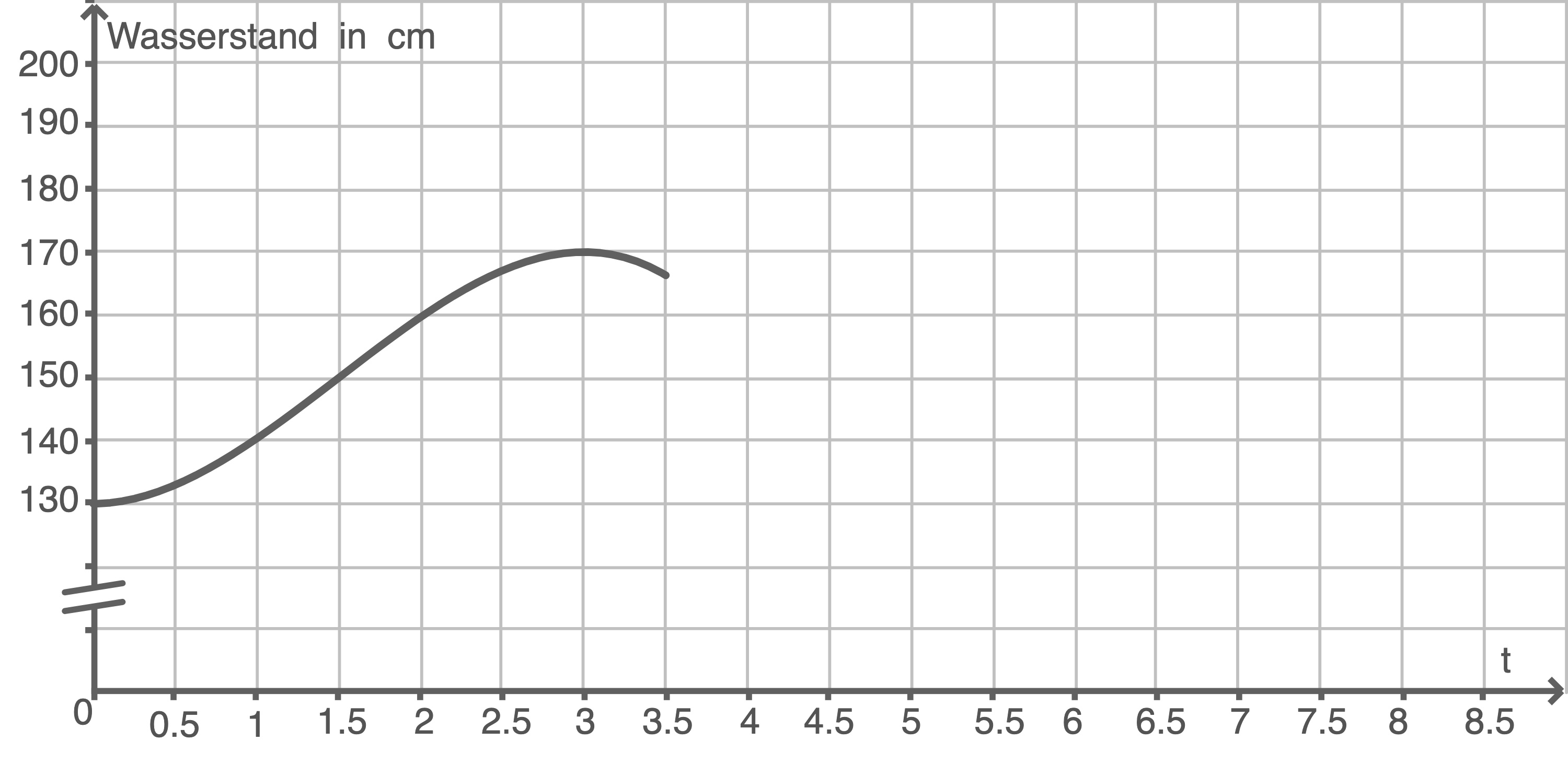
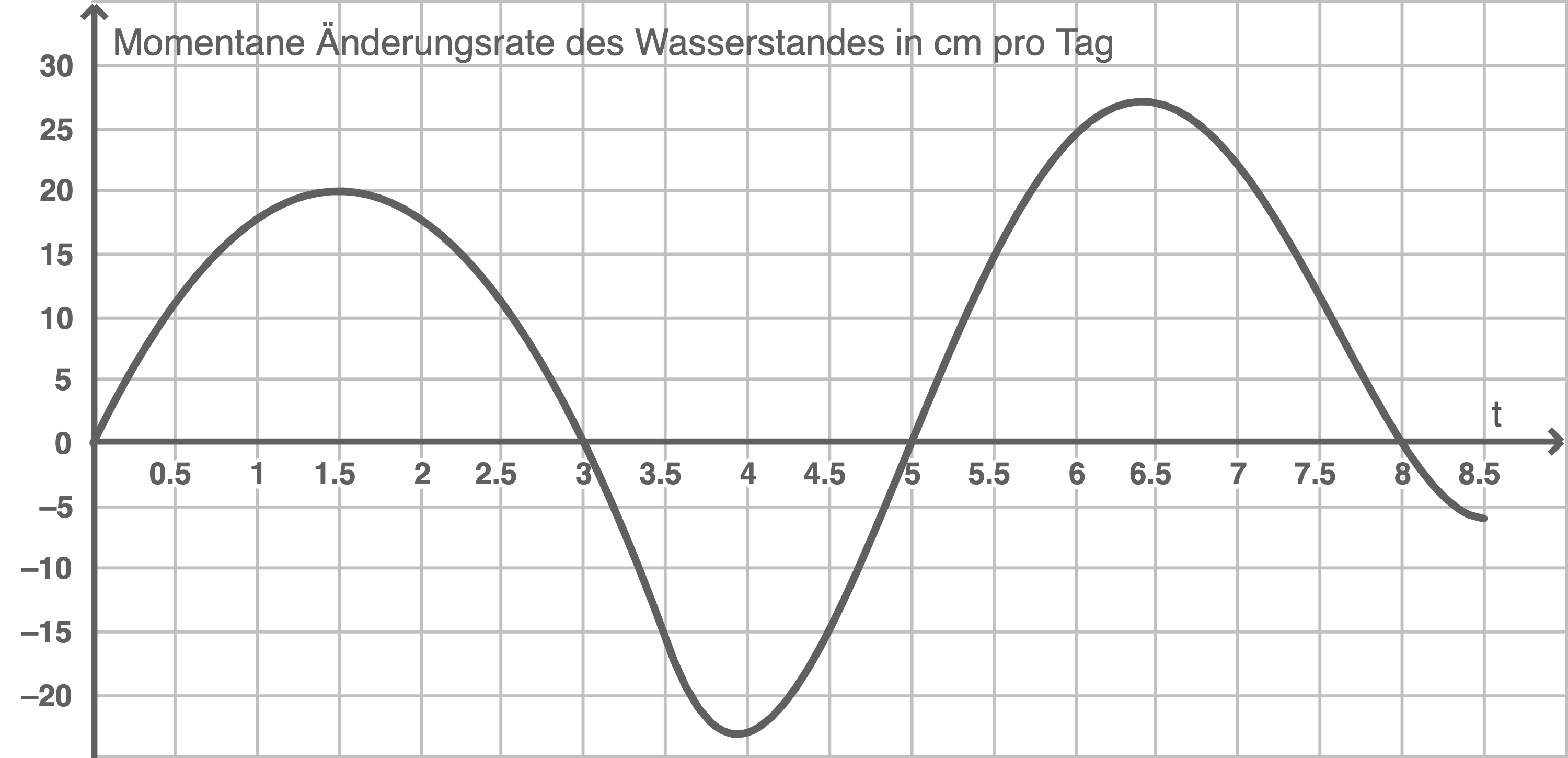 Skizziere, passend zu der in Abbildung 4 gegebenen momentanen Änderungsrate, in Abbildung 3 den weiteren Verlauf des Wasserstandes bis zum 28.10.2016, 12:00 Uhr.
Skizziere, passend zu der in Abbildung 4 gegebenen momentanen Änderungsrate, in Abbildung 3 den weiteren Verlauf des Wasserstandes bis zum 28.10.2016, 12:00 Uhr.
Die Abbildung 4 zeigt die momentane Änderungsrate des Wasserstandes im verlängerten Zeitraum vom 20.10.2016, 0:00 Uhr, bis zum 28.10.2016, 12:00 Uhr

Abbildung 3

Abbildung 4
(4 Punkte)
[1] Der Wasserstand ist die Höhe des Wassers an einer Messstelle (Pegel) und entspricht nicht der Wassertiefe des Flusses.
Lösung 3
a)
Die Gleichung  kann mit dem solve-Befehl des CAS gelöst werden. Bei
kann mit dem solve-Befehl des CAS gelöst werden. Bei  handelt es sich um die Lösung, die zwischen
handelt es sich um die Lösung, die zwischen  und
und  liegt.
Mit dem CAS ergibt sich:
liegt.
Mit dem CAS ergibt sich: 
b)
1. Notwendiges Kriterium für lokale Extremstelle überprüfen
Für eine lokale Maximalstelle  von
von  muss das notwendige Kriterium
muss das notwendige Kriterium  erfüllt sein.
erfüllt sein.
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/d2329197132fb2f64a52870477e5978bb3798707b1c138142de9c511a4e0b974?color=5a5a5a) Einsetzen von
Einsetzen von  ergibt:
ergibt:
 2. Vorzeichenwechselkriterium überprüfen
Um sicherzugehen, dass es sich um eine Maximalstelle und nicht um eine Minimalstelle handelt, muss das Vorzeichenwechselkriterium überprüft werden:
2. Vorzeichenwechselkriterium überprüfen
Um sicherzugehen, dass es sich um eine Maximalstelle und nicht um eine Minimalstelle handelt, muss das Vorzeichenwechselkriterium überprüft werden:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/8570af9401900f066ff5ef4f4a49ce888b80142137ea05cb4490844d86d59286?color=5a5a5a) Der Graph von
Der Graph von  hat also unmittelbar vor der Stelle
hat also unmittelbar vor der Stelle  eine positive Steigung und unmittelbar danach eine negative. Der Graph steigt also zunächst und fällt nach der Stelle
eine positive Steigung und unmittelbar danach eine negative. Der Graph steigt also zunächst und fällt nach der Stelle  Daher handelt es sich bei
Daher handelt es sich bei  um eine lokale Maximalstelle.
um eine lokale Maximalstelle.
c)
(1)
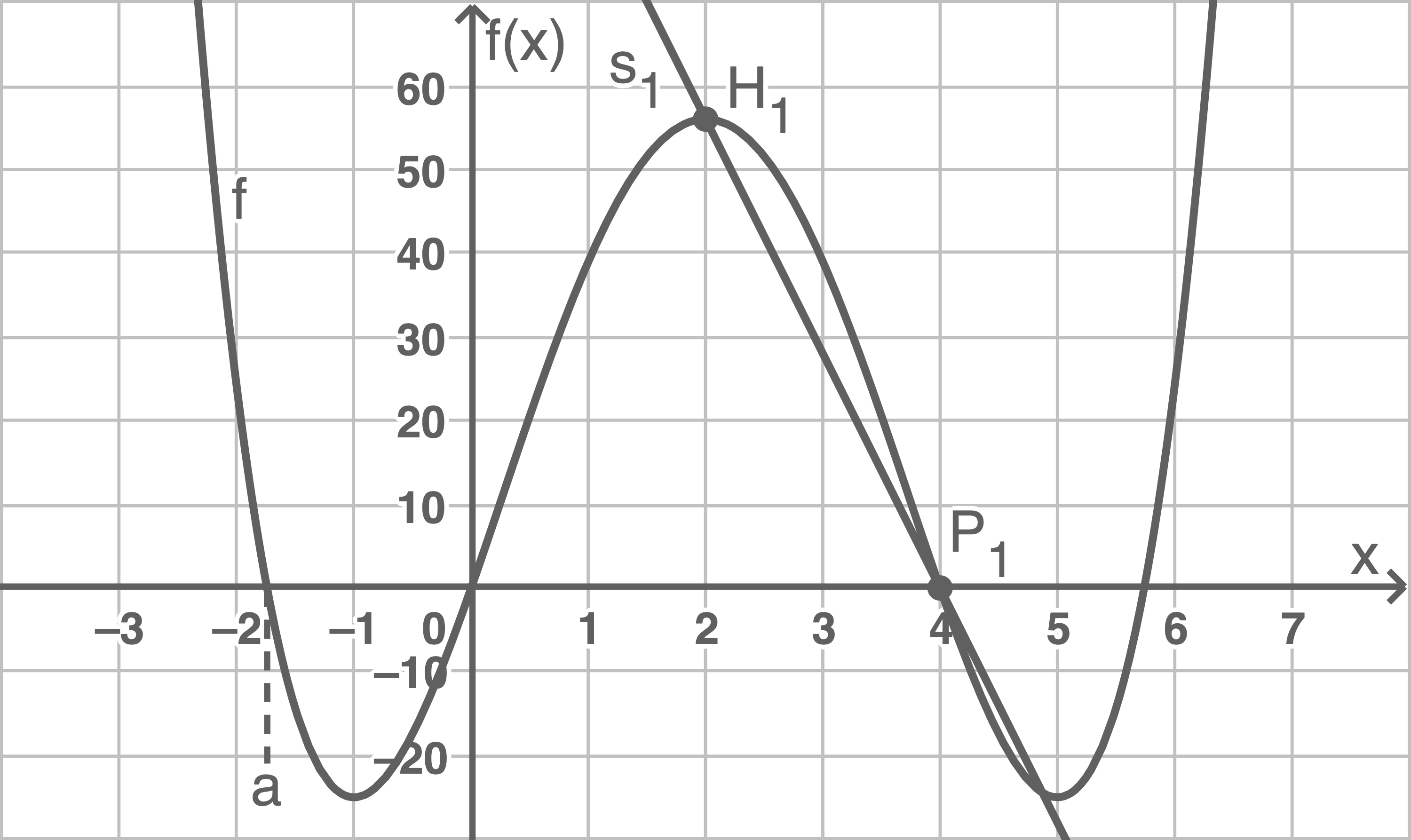
(2)
Gleichung einer Tangente 
![\(\begin{array}[t]{rll}
m_t&=& f](https://mathjax.schullv.de/179413f4ab4b48921774a4d6448d5c0a9b3a9d2b121105b4c6b8a0cd876cf960?color=5a5a5a) Es gilt:
Es gilt:  Punkt
Punkt  in Tangentengleichung einsetzen:
in Tangentengleichung einsetzen:
![\(\begin{array}[t]{rll}
t:y&=& -40\cdot x +b_t \quad \scriptsize \mid\; P_1(4\mid 0)\\[5pt]
0&=& -40\cdot 4 +b_t \\[5pt]
0&=& -160 + b_t \quad \scriptsize \mid\; +160 \\[5pt]
160&=& b_t
\end{array}\)](https://mathjax.schullv.de/5d9addd53a3ae900ca3f477ff2c498a5d7866cd74979ebd034f5624c2c85a52a?color=5a5a5a) Eine Gleichung der Tangente
Eine Gleichung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  lautet also:
lautet also:

(3)
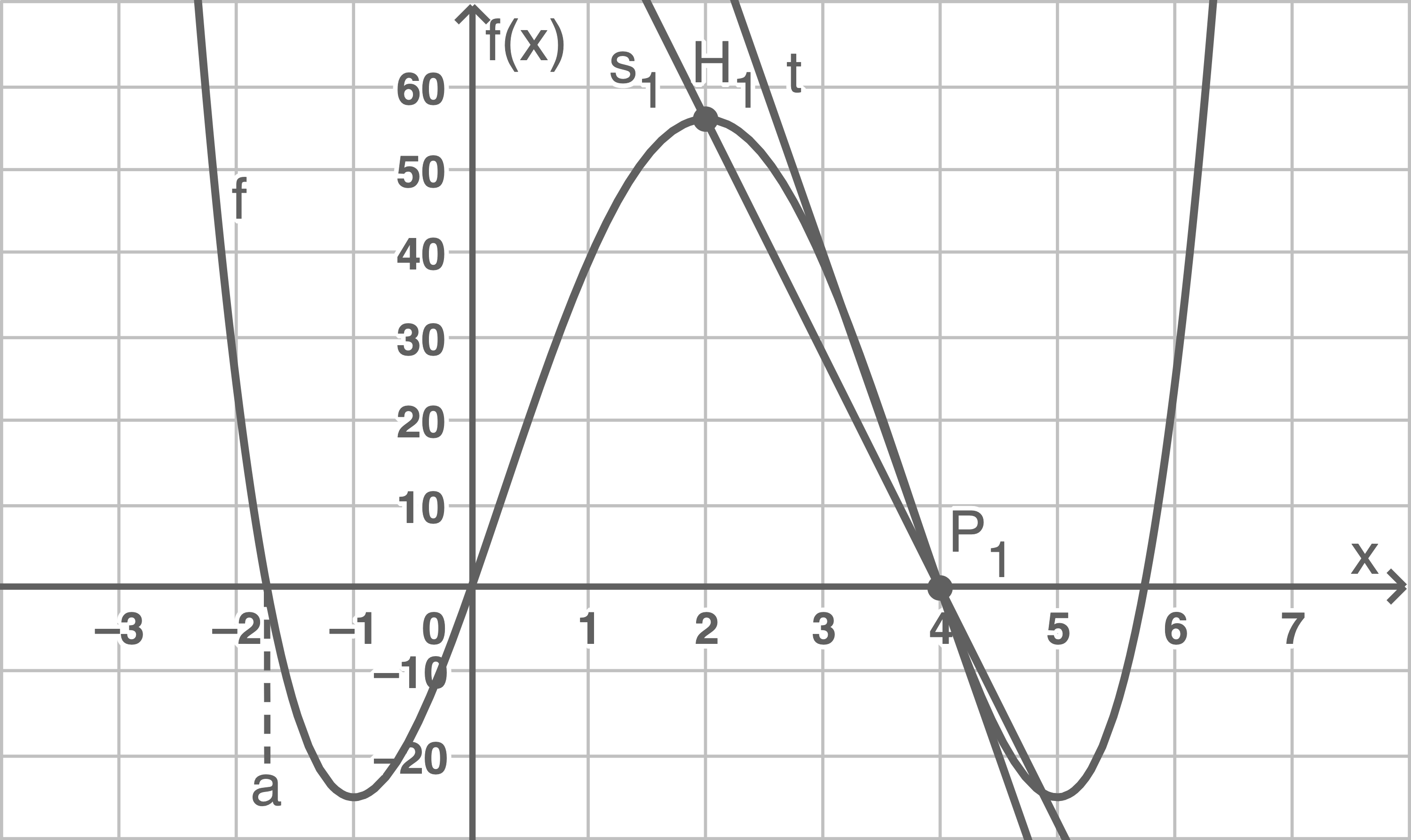
(4)
Je näher  an
an  liegt, desto näher kommt die Steigung der Sekante durch
liegt, desto näher kommt die Steigung der Sekante durch  und
und  an die Steigung der Tangente in
an die Steigung der Tangente in  Beispielsweise kann mit der Stelle
Beispielsweise kann mit der Stelle  gestartet werden:
gestartet werden:
 Die Steigung der Sekante in diesem Fall:
Die Steigung der Sekante in diesem Fall:
![\(\begin{array}[t]{rll}
m&=& \dfrac{0 - 4,0521}{4-3.9}&\quad \scriptsize \\[5pt]
&=& -40,521
\end{array}\)](https://mathjax.schullv.de/7c30f61d438ea996a59344b2dcc18b35d83a5b90a2aa1a4cdcf5898adba7b3c0?color=5a5a5a) Da die Steigung noch zu groß ist, handelt es sich um einen Wert zwischen
Da die Steigung noch zu groß ist, handelt es sich um einen Wert zwischen  und
und  beispielsweise
beispielsweise 
 Die Steigung der Sekante in diesem Fall:
Die Steigung der Sekante in diesem Fall:
![\(\begin{array}[t]{rll}
m&=& \dfrac{0-0,4006}{4-3,99}&\quad \scriptsize \\[5pt]
&=& -40,06
\end{array}\)](https://mathjax.schullv.de/95c756bf1a821db5b6e0425d8a96098d50bad0c82f0b0049fc1679d76941973a?color=5a5a5a) Hier ist die Abweichung zu
Hier ist die Abweichung zu  weniger als 0,1.
weniger als 0,1.
Ein Punkt, der die Bedingung erfüllt, ist also
Ein Punkt, der die Bedingung erfüllt, ist also
d)
1. Schritt: Gleichung des gestauchten Graphen bestimmen
Eine Stauchung oder Streckung in  -Richtung erfolgt durch einen Faktor
-Richtung erfolgt durch einen Faktor  Die Gleichung der Funktion
Die Gleichung der Funktion  zum gestauchten Graphen von
zum gestauchten Graphen von  lautet also:
lautet also:

 bestimmen, sodass
bestimmen, sodass  gilt:
gilt:
![\(\begin{array}[t]{rll}
28&=& g_1(2) &\quad \scriptsize \\[5pt]
28&=& a\cdot f(2) \\[5pt]
28&=& a\cdot 56 \quad \scriptsize \mid\; :56\\[5pt]
\dfrac{1}{2}&=& a
\end{array}\)](https://mathjax.schullv.de/30001dcb9102b27d2ed6a1c77e7df2f83b29fb15b8e66177ed4180cf0b0f0a46?color=5a5a5a) Eine Gleichung zum gestauchten Graphen lautet also
Eine Gleichung zum gestauchten Graphen lautet also
![\(\begin{array}[t]{rll}
g_1(x)&=& \dfrac{1}{2}\cdot f(x)&\quad \scriptsize \\[5pt]
&=& \dfrac{1}{2}\cdot (x^4-8x^3+6x^2+40x )
\end{array}\)](https://mathjax.schullv.de/2419e1e1abf78eb86844c8ebbd5c0de7ac6a7107e9d8800391b9f26a8f823c06?color=5a5a5a) 2. Schritt: Gleichung des verschobenen Graphen angeben
Der Graph von
2. Schritt: Gleichung des verschobenen Graphen angeben
Der Graph von  entsteht nun durch Verschiebung um
entsteht nun durch Verschiebung um  Einheiten in
Einheiten in  -Richtung:
-Richtung:
Lösung 4
a)
Der Wasserstand am 21.10.2016 um 12:00 Uhr wird durch  beschrieben:
beschrieben:
![\(\begin{array}[t]{rll}
h(1,5)&=& -\dfrac{80}{27}\cdot 1,5^3 +\dfrac{40}{3}\cdot 1,5 ^2 +130 &\quad \scriptsize \\[5pt]
&=& 150
\end{array}\)](https://mathjax.schullv.de/da113b16e5636690ba5d069c7901c08b112a534a1b1179ad77be3c35c264baed?color=5a5a5a) Am 21.10.2016 um 12:00 Uhr betrug der Wasserstand des Rheins an der Messstelle in Bonn
Am 21.10.2016 um 12:00 Uhr betrug der Wasserstand des Rheins an der Messstelle in Bonn 
b)
Der Wert ist der Differenzenquotient aus den beiden Punkten  und
und  und entspricht daher der Steigung der Sekante durch diese beiden Punkte.
und entspricht daher der Steigung der Sekante durch diese beiden Punkte.
Im Sachzusammenhang bedeutet dies, dass der Wasserstand des Rheins an der Messtelle in Bonn zwischen dem um 0:00 Uhr und dem 23.10.2016 um 0:00 Uhr um durchschnittlich
um 0:00 Uhr und dem 23.10.2016 um 0:00 Uhr um durchschnittlich  pro Tag gestiegen ist.
pro Tag gestiegen ist.
Im Sachzusammenhang bedeutet dies, dass der Wasserstand des Rheins an der Messtelle in Bonn zwischen dem
c)
1. Schritt: Notwendiges Kriterium für lokale Extremstellen anwenden
![\(\begin{array}[t]{rll}
h(t)&=& -\dfrac{80}{27}\cdot t^3 +\dfrac{40}{3}\cdot t^2 +130 \\[5pt]
h](https://mathjax.schullv.de/68fedcfa9a7a145b7759a01a4c9b60808588dddcc811515a97bbbe1a0c7be3e0?color=5a5a5a) Als Lösung der Gleichung
Als Lösung der Gleichung  liefert der solve-Befehl des CAS die Nullstellen
liefert der solve-Befehl des CAS die Nullstellen  und
und  2. Schritt: Vorzeichenwechselkriterium überprüfen
2. Schritt: Vorzeichenwechselkriterium überprüfen
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/5757a1d9dc6704237837cf6fcd57c15bd7d777ccbcfcca50383eab571dc9e5db?color=5a5a5a) An der Stelle
An der Stelle  liegt eine lokale Maximalstelle vor. Da
liegt eine lokale Maximalstelle vor. Da  am Rand des Definitionsbereich liegt, muss diese Stelle separat überprüft werden.
3. Schritt: Funktionswerte vergleichen
Betrachtet wird der Bereich
am Rand des Definitionsbereich liegt, muss diese Stelle separat überprüft werden.
3. Schritt: Funktionswerte vergleichen
Betrachtet wird der Bereich  Den höchsten und den niedrigsten Funktionswert kann
Den höchsten und den niedrigsten Funktionswert kann  entweder in den beiden möglichen lokalen Extremstellen oder in den Intervallrändern annehmen.
Funktionswerte in diesen Stellen vergleichen:
entweder in den beiden möglichen lokalen Extremstellen oder in den Intervallrändern annehmen.
Funktionswerte in diesen Stellen vergleichen:
![\(\begin{array}[t]{rll}
h(0)&=& -\dfrac{80}{27}\cdot 0^3 +\dfrac{40}{3}\cdot 0^2 +130 \\[5pt]
&=& 130 \\[10pt]
h(3)&=& -\dfrac{80}{27}\cdot 3^3 +\dfrac{40}{3}\cdot 3^2 +130 \\[5pt]
&=& 170 \\[10pt]
h(3,5)&=& -\dfrac{80}{27}\cdot 3,5^3 +\dfrac{40}{3}\cdot 3,5^2 +130 \\[5pt]
&\approx& 166,3
\end{array}\)](https://mathjax.schullv.de/9cd01c1e646b0e31ccfd2790c699c5f1e84dfa6fdd9844fa6e66836c4c9ecbee?color=5a5a5a) Da zwischen den Rändern des Definitionsbereichs nur ein lokales Maximum liegt, muss das globale Minimum der Funktion auf dem Rand liegen. Der höchste Wasserstand im betrachteten Zeitraum ist
Da zwischen den Rändern des Definitionsbereichs nur ein lokales Maximum liegt, muss das globale Minimum der Funktion auf dem Rand liegen. Der höchste Wasserstand im betrachteten Zeitraum ist  der niedrigste ist
der niedrigste ist 
d)
Es müssen die Stellen im betrachteten Bereich berechnet werden, für die  bzw.
bzw.  gilt. Dazu kannst der solve-Befehl des CAS verwendet werden.
Es ergeben sich folgende Lösungen im betrachteten Bereich:
gilt. Dazu kannst der solve-Befehl des CAS verwendet werden.
Es ergeben sich folgende Lösungen im betrachteten Bereich:
![\(\begin{array}[t]{rll}
h(0,98)&\approx& 140 \\[5pt]
h(1,5)&=& 150
\end{array}\)](https://mathjax.schullv.de/e6c7630dfafb2885e33ab7cdd6af9ae38489b54b0561664e3e5aea921739acb7?color=5a5a5a)
 Der Wasserstand lag also ca. einen halben Tag zwischen
Der Wasserstand lag also ca. einen halben Tag zwischen  und
und 
e)