SchulLV Logo
Lerninhalte in Mathe
Inhaltsverzeichnis

Prüfungsteil A: Ohne Hilfsmittel

Aufgabe 1

Gegeben ist die Funktion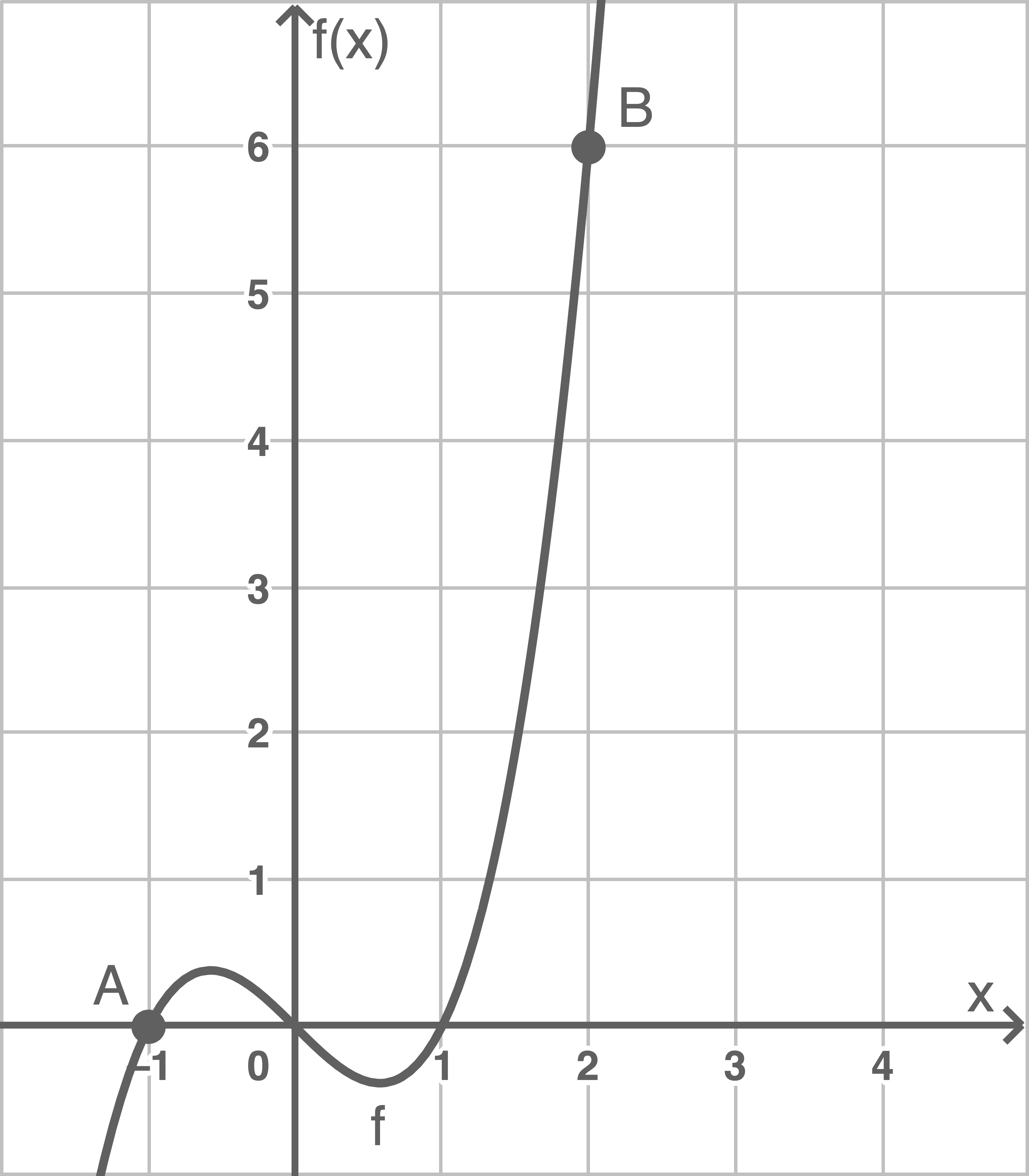 \(f\) mit \(f(x) = x^3 - x,\,\, x \in \mathbb{R}.\)
Die Abbildung zeigt den Graphen von \(f\).
nrw zk 2021 abbildung aufgabe 1
Abbildung
a)
Bestimme die Steigung \(m\) der Sekante durch die Punkte \(A (-1 \mid 0)\) und \(B(2 \mid 6).\)
(2 Punkte)
b)
Berechne alle Stellen, an denen der Graph der Funktion \(f\) die Steigung 2 besitzt.
(4 Punkte)

Aufgabe 2

Zwei Würfel sind wie folgt beschriftet: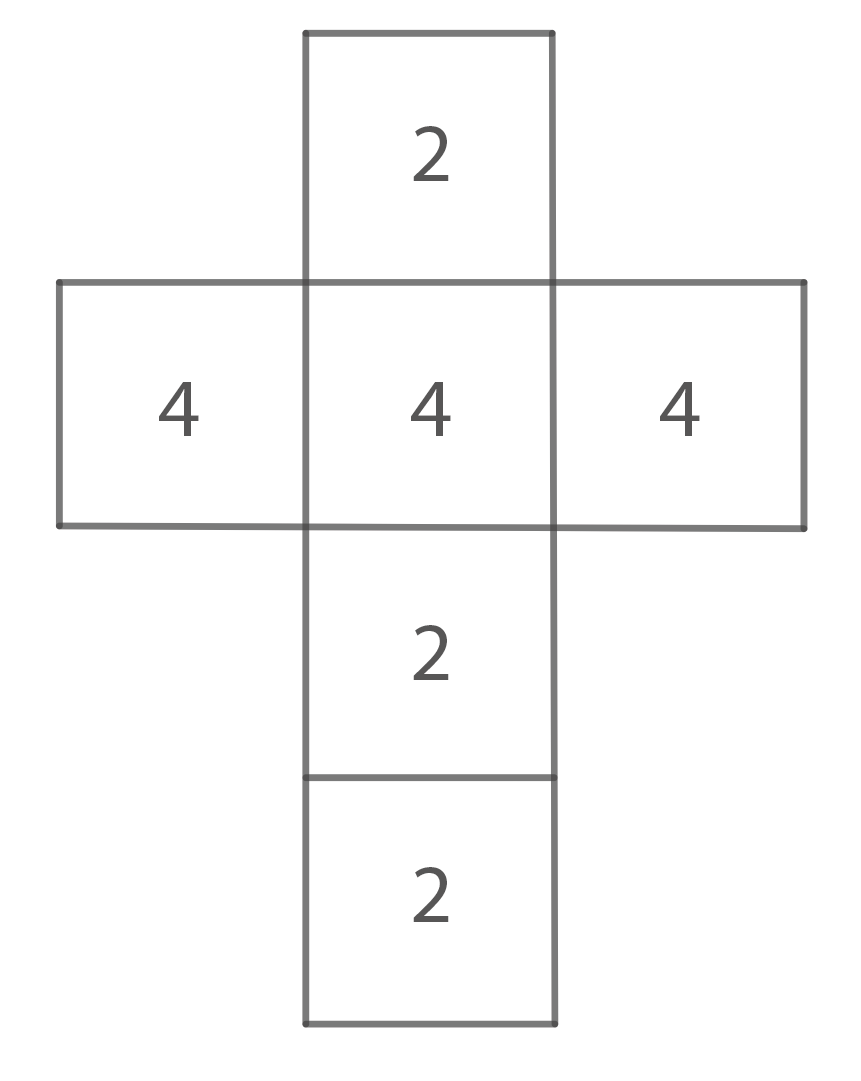
Diagramm mit Zahlen in verschiedenen Feldern angeordnet, die eine Kreuzform bilden.
Würfel A
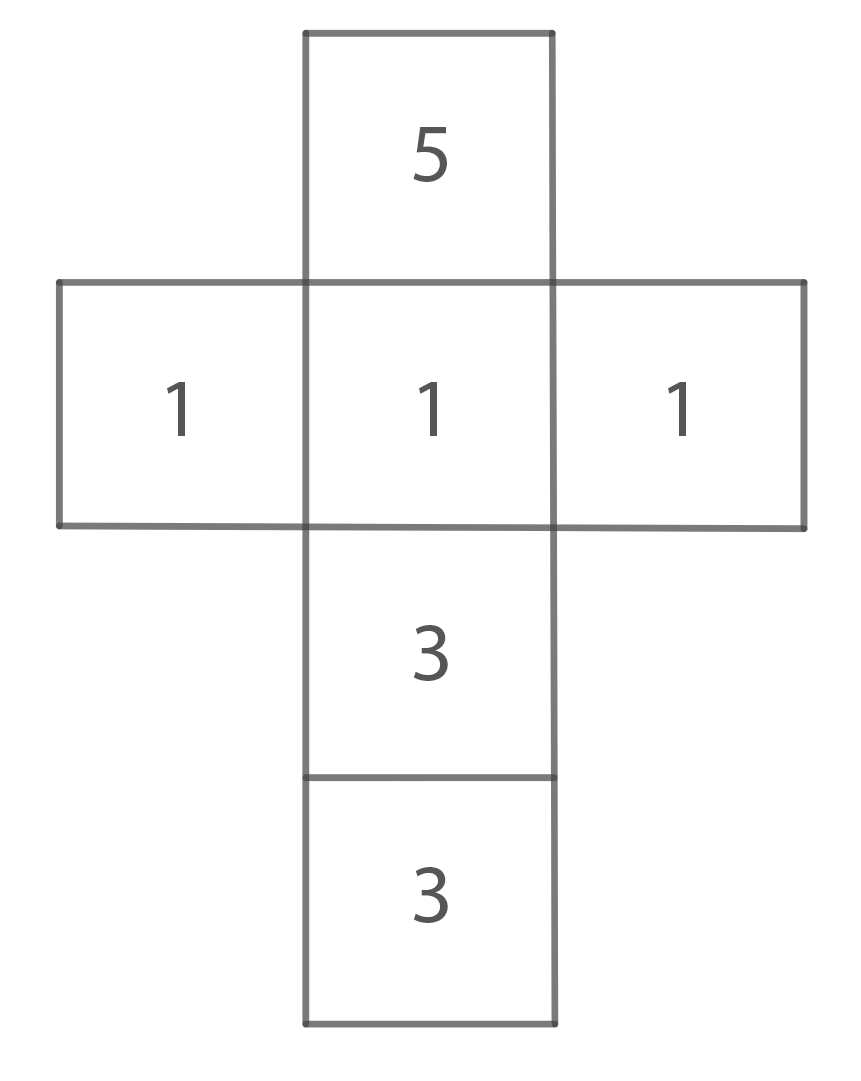
Kreuzförmige Anordnung von Zahlen 1, 3 und 5 in einem minimalistischen Design.
Würfel B
Bei einem Spiel wird zunächst Würfel A und dann Würfel B geworfen. Der Spieler gewinnt, wenn die Augenzahl von Würfel B größer ist als die Augenzahl von Würfel A.
(1)
Erstelle für dieses Spiel ein vollständig beschriftetes Baumdiagramm mit allen Pfadwahrscheinlichkeiten.
(2)
Ermittle die Wahrscheinlichtkeit dafür, dass der Spieler das Spiel gewinnt.
(3)
Die Augenzahlen von Würfel B sollen so verändert werden, dass die Wahrscheinlichkeit für den Gewinn eines Spiels 50 % beträgt.
Gib eine Beschriftung von Würfel B an, bei der diese Bedingung erfüllt ist.
(2 + 2 + 2 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
  • Link zur App im AppStoreLink zur App im PlayStore

SchulLV