Prüfungsteil B: Mit Hilfsmitteln
Aufgabe 3
Gegeben ist die Funktion
a)
Bestimme (gerundet auf zwei Nachkommastellen) die Nullstellen der Funktion 
(3 P)
b)
Zeige rechnerisch, dass  eine lokale Minimalstelle der Funktion
eine lokale Minimalstelle der Funktion  ist.
ist.
(6 P)
c)
Ausgehend von der Funktion  ist eine neue Funktion
ist eine neue Funktion  mit der Gleichung
gegeben. Die Abbildung 1 auf der folgenden Seite zeigt den Graphen von
mit der Gleichung
gegeben. Die Abbildung 1 auf der folgenden Seite zeigt den Graphen von  , die Abbildung 2 zeigt den Graphen von
, die Abbildung 2 zeigt den Graphen von  Nenne zwei Unterschiede der Graphen von
Nenne zwei Unterschiede der Graphen von  und
und 
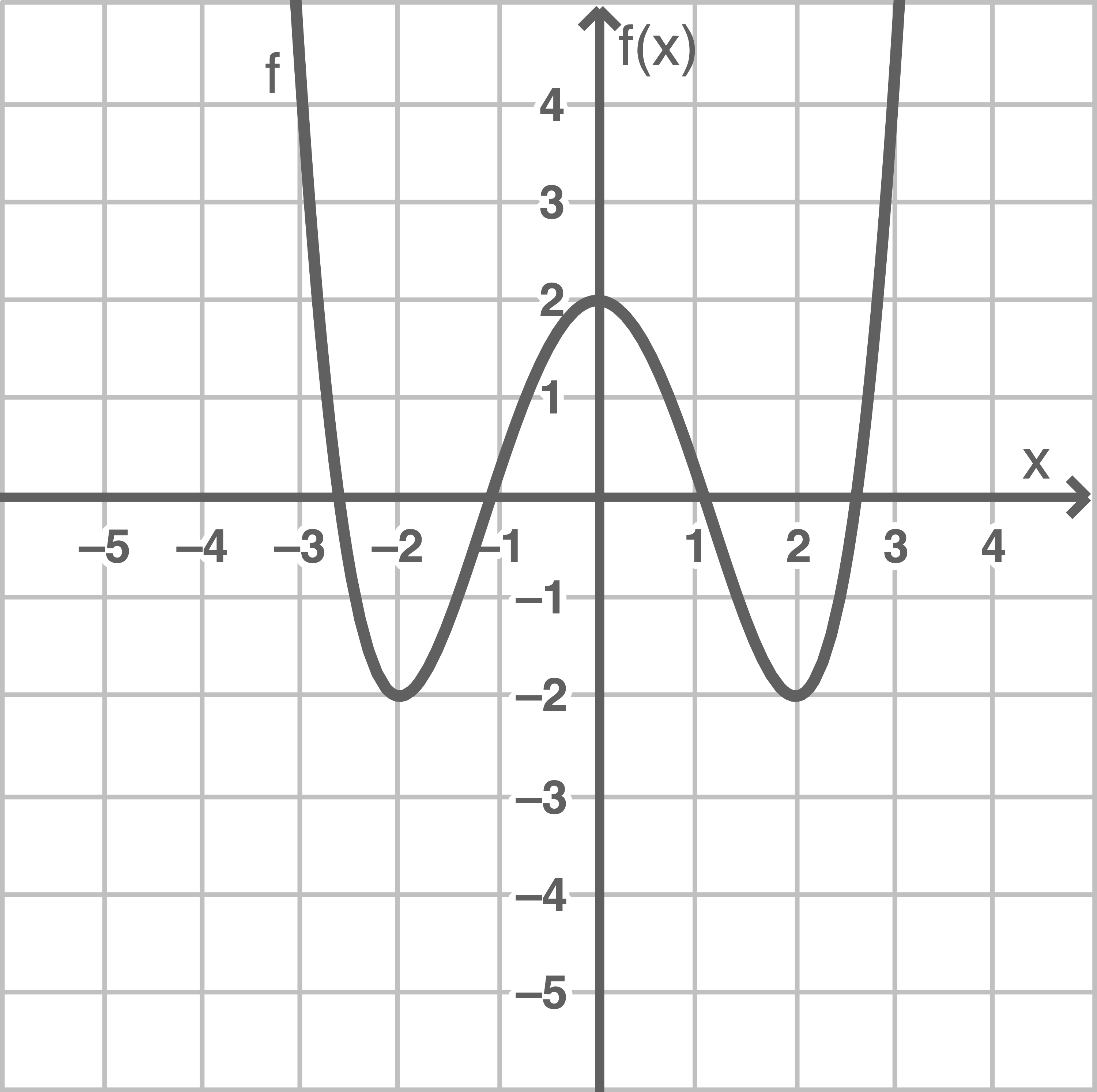
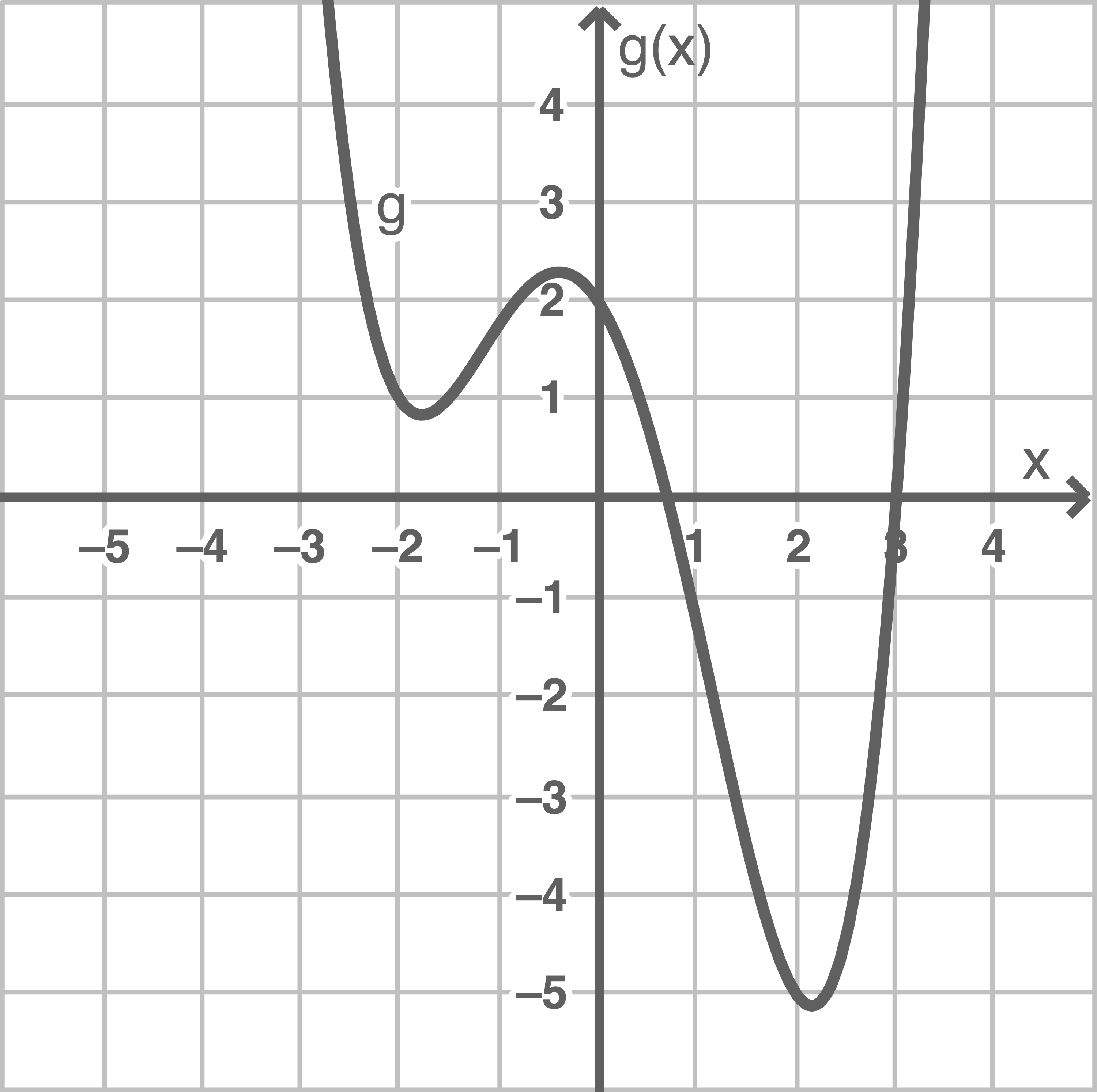

Abbildung 1

Abbildung 2
d)
Die Gerade  ist die Tangente an den Graphen von
ist die Tangente an den Graphen von  im Punkt
im Punkt 
[Hinweis: Ein Nachweis, dass die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  ist, ist nicht erforderlich.]
ist, ist nicht erforderlich.]
[Hinweis: Ein Nachweis, dass
(1)
Zeichne die Tangente  in die Abbildung 2 ein.
in die Abbildung 2 ein.
(2)
Zeige rechnerisch, dass  auch in einem weiteren Punkt
auch in einem weiteren Punkt  Tangente an den Graphen von
Tangente an den Graphen von  ist.
ist.
(2+6 P)
e)
Der Graph von  wird nun um
wird nun um  Einheiten nach rechts verschoben. Der verschobene Graph wird anschließend so weit nach unten verschoben, bis die Gerade
Einheiten nach rechts verschoben. Der verschobene Graph wird anschließend so weit nach unten verschoben, bis die Gerade  in zwei Punkten Tangente an den neuen Graphen ist.
Gib an, um wie viele Einheiten der nach rechts verschobene Graph dazu nach unten verschoben werden muss, und begründe deine Angabe.
in zwei Punkten Tangente an den neuen Graphen ist.
Gib an, um wie viele Einheiten der nach rechts verschobene Graph dazu nach unten verschoben werden muss, und begründe deine Angabe.
(3 P)
Aufgabe 4
Ausgehend von Daten aus einer Statistik der Vereinten Nationen kann das Durchschnittsalter der Bevölkerung in einem LandMit der Funktion
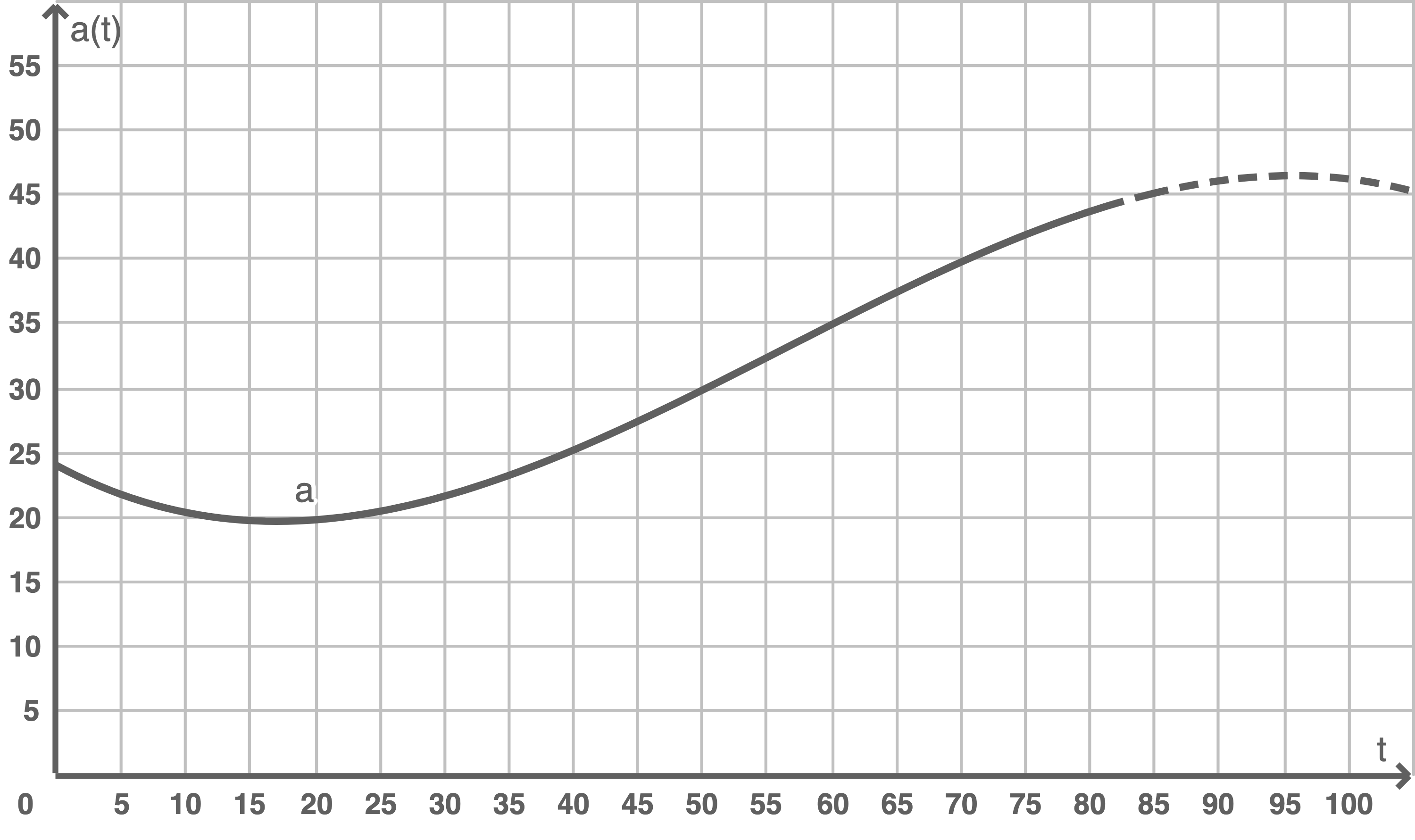
Abbildung 1
a)
Bestimme das Durchschnittsalter der Bevölkerung für das Jahr 1950  und den Prognosewert für das Jahr 2030
und den Prognosewert für das Jahr 2030 
(4 P)
b)
Ermittle rechnerisch das niedrigste Durchschnittsalter der Bevölkerung im Zeitraum von 1950 bis 2030.
(8 P)
c)
Die Entwicklung des Durchschnittsalters der Bevölkerung im Zeitraum von 2030 bis 2050 soll durch die Tangente an den Graphen von  an der Stelle
an der Stelle  modelliert werden.
Ermittle in Abbildung 1 rechnerisch näherungsweise das Durchschnittsalter der Bevölkerung für das Jahr 2050.
modelliert werden.
Ermittle in Abbildung 1 rechnerisch näherungsweise das Durchschnittsalter der Bevölkerung für das Jahr 2050.
(3 P)
d)
In einem anderen Land  stimmte für das Jahr 1950
stimmte für das Jahr 1950  das Durchschnittsalter der Bevölkerung nahezu mit dem Durchschnittsalter in dem Land
das Durchschnittsalter der Bevölkerung nahezu mit dem Durchschnittsalter in dem Land  überein. Die Rate, mit der sich das Durchschnittsalter der Bevölkerung in dem Land
überein. Die Rate, mit der sich das Durchschnittsalter der Bevölkerung in dem Land  ändert, ist in der folgenden Abbildung 4 dargestellt.
ändert, ist in der folgenden Abbildung 4 dargestellt.
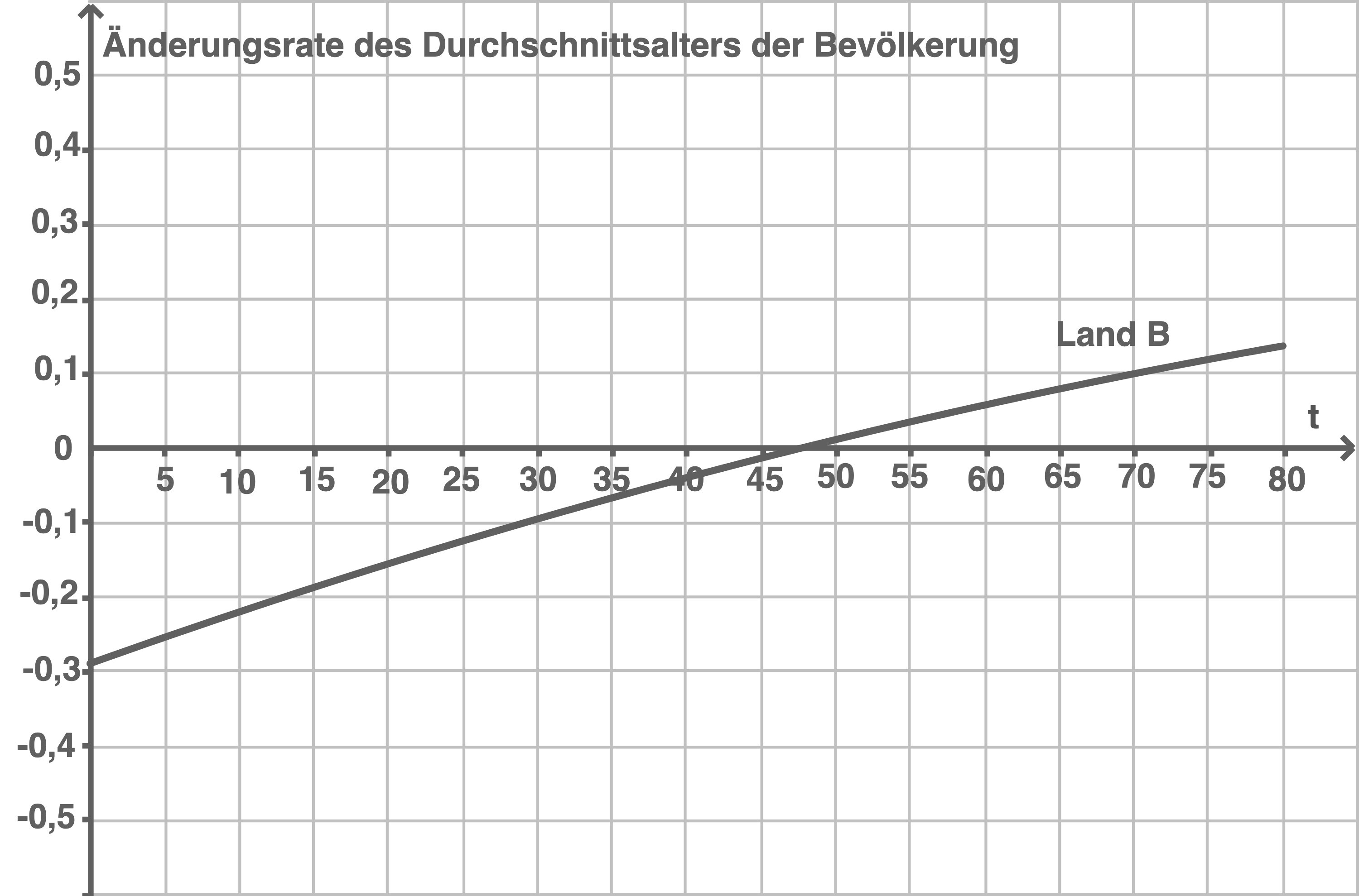
Bildnachweise [nach oben]

Abbildung 2
(1)
Beurteile die folgende Aussage:
Das Durchschnittsalter der Bevölkerung in dem Land  wächst von 1950 bis 2030 durchgängig.
wächst von 1950 bis 2030 durchgängig.
(2)
Zeichne den Graphen der Ableitungsfunktion  in die Abbildung 4 ein und gib die Bedeutung von
in die Abbildung 4 ein und gib die Bedeutung von  im Sachzusammenhang an.
im Sachzusammenhang an.
(3)
Beurteile die folgende Aussage:
Im Jahr 2020 wächst das Durchschnittsalter der Bevölkerung in dem Land  schneller als in dem Land
schneller als in dem Land 
(2+5+2 P)
© 2017 - SchulLV.
© 2017 - SchulLV.
© 2017 - SchulLV.
© 2017 - SchulLV.
Lösung 3
a)
Für die Nullstellen der Funktion  folgt mit dem Grafik-Modus des CAS:
folgt mit dem Grafik-Modus des CAS:
 ,
,  ,
,  und
und 
b)
1. Schritt: Ableitung bestimmen
Für die Ableitungsfunktion der Funktion  gilt:
gilt:
![\(\begin{array}[t]{rll}
f(x)&=& \dfrac{1}{4} \cdot x^4 -2 \cdot x^2 +2 \\[5pt]
f](https://mathjax.schullv.de/4098a2415bb2eb8552324484b419b9cd0fc8beb2d28f03189bf3e64944db7c37?color=5a5a5a) 2. Schritt: Notwendiges Kiterium für Extremstellen überprüfen
Mit dem notwendigen Kriterium
2. Schritt: Notwendiges Kiterium für Extremstellen überprüfen
Mit dem notwendigen Kriterium  für eine lokale Extremstelle folgt:
für eine lokale Extremstelle folgt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/a8a09c6e15156ffbb585aa2096fa547b2ca29499ef2d16206852d7f42991708e?color=5a5a5a) Mit dem Satz vom Nullprodukt gilt:
Mit dem Satz vom Nullprodukt gilt:
![\(\begin{array}[t]{rll}
x_1 &=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/829a78b1edda5611afc6f295dd5f9f7740ed55a447f77790abd51dd8710ede0b?color=5a5a5a)
![\(\begin{array}[t]{rll}
x^2-4 &=& 0 \quad \scriptsize \mid\; +4 \\[5pt]
x^2 &=& 4 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
x_2 &=& 2 \\[5pt]
x_3 &=& -2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/1e946af257fb2953ca189d1678d7a78556de660f1c67720a20c3a4145721d816?color=5a5a5a) 3. Schritt: Vorzeichenwechsel-Kriterium anwenden
3. Schritt: Vorzeichenwechsel-Kriterium anwenden
![\(\begin{array}[t]{rll}
f‘(1)&=& 1^3 -4 \cdot 1 \\[5pt]
&=& -3 \quad \lt 0
\end{array}\)](https://mathjax.schullv.de/0233c3a13f06eaa5d0f16b17dcdbe96d8a9a465975cc7b1417947d1ba1eac199?color=5a5a5a)
![\(\begin{array}[t]{rll}
f‘(3)&=& 3^3 -4 \cdot 3 \\[5pt]
&=& 15 \quad \gt 0
\end{array}\)](https://mathjax.schullv.de/5d0ff76c674395024172bef38a70b4b5f363afa4754716841315fe667d5332ff?color=5a5a5a) Somit besitzt der Graph der Ableitungsfunktion an der Stelle
Somit besitzt der Graph der Ableitungsfunktion an der Stelle  einen Vorzeichenwechsel von negativen zu positiven Funktionswerten. Damit ist das hinreichende Kriterium für eine lokale Minimalstelle erfüllt und der Graph der Funktion
einen Vorzeichenwechsel von negativen zu positiven Funktionswerten. Damit ist das hinreichende Kriterium für eine lokale Minimalstelle erfüllt und der Graph der Funktion  besitzt an der Stelle
besitzt an der Stelle  eine lokale Minimalstelle.
eine lokale Minimalstelle.
c)
Es können beispielsweise die folgenden beiden Unterschiede genannt werden:
- Der Graph der Funktion
ist achsensymmetrisch zur
-Achse, wobei der Graph der Funktion
keine Symmetrie aufweist.
- Der Graph der Funktion
besitzt vier und der Graph der Funktion
insgesamt zwei Nullstellen.
d)
(1)
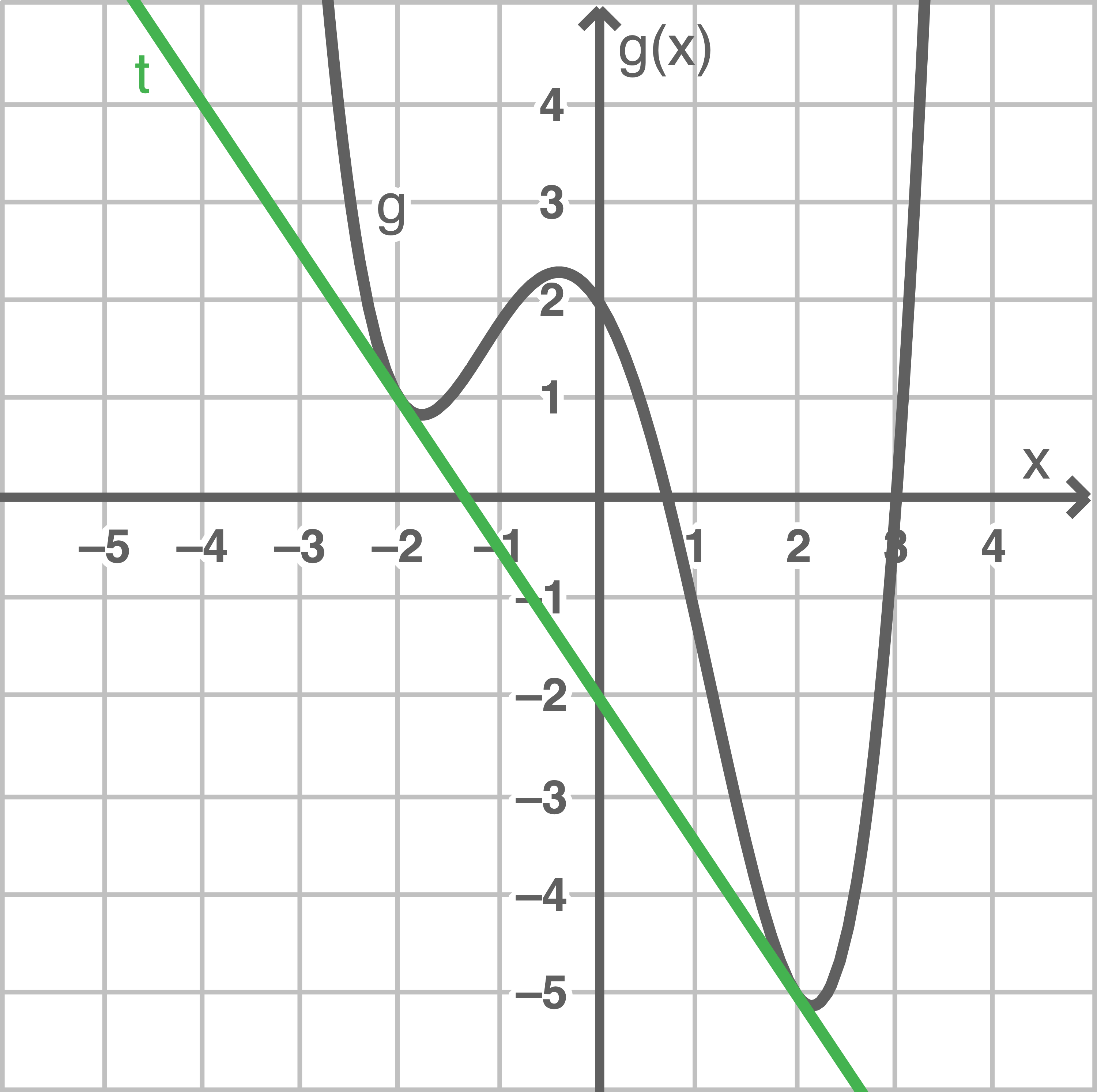
(2)
Für die gemeinsamen Punkte der Tangente  und dem Graphen der Funktion
und dem Graphen der Funktion  folgt durch Gleichsetzen der Funktionsgleichungen:
Dadurch besitzen die Tangente
folgt durch Gleichsetzen der Funktionsgleichungen:
Dadurch besitzen die Tangente  und der Graph der Funktion
und der Graph der Funktion  an den Stellen
an den Stellen  und
und  einen gemeinsamen Punkt.
Für eine Tangente an der Stelle
einen gemeinsamen Punkt.
Für eine Tangente an der Stelle  muss außerdem gelten, dass die Steigung der Tangente gleich der Steigung von
muss außerdem gelten, dass die Steigung der Tangente gleich der Steigung von  an der Stelle
an der Stelle  ist. Für die Ableitungsfunktion der Funktion
ist. Für die Ableitungsfunktion der Funktion  folgt:
folgt:
![\(\begin{array}[t]{rll}
g(x)&=& \dfrac{1}{4} \cdot x^4 -2 \cdot x^2 - \dfrac{3}{2} \cdot x +2 \\[5pt]
g](https://mathjax.schullv.de/55cac8dca3d0b11ccf612c99f9d1d1966d4390029b94fde20f7161eab30573f4?color=5a5a5a) Damit folgt für
Damit folgt für  :
:
![\(\begin{array}[t]{rll}
g](https://mathjax.schullv.de/8d3291f96311ca68f612aca7a240c5f276a54e5d0ba217379d732449b64a5b7b?color=5a5a5a) Somit gilt, dass die Steigung des Graphen von
Somit gilt, dass die Steigung des Graphen von  an der Stelle
an der Stelle  gleich der Steigung der Tangente ist. Deshalb ist die Tangente
gleich der Steigung der Tangente ist. Deshalb ist die Tangente  in dem Punkt
in dem Punkt  auch eine Tangente an den Graphen von
auch eine Tangente an den Graphen von 
e)
Die Steigung der Tangente ist durch  gegeben. Da der Graph der Funktion
gegeben. Da der Graph der Funktion  um
um  Einheiten nach rechts verschoben wird, muss er um
Einheiten nach rechts verschoben wird, muss er um  Einheiten nach unten verschoben werden, damit die Verschiebung entlang der Tangente verläuft.
Einheiten nach unten verschoben werden, damit die Verschiebung entlang der Tangente verläuft.
Lösung 4
a)
Durchschnittsalter bestimmen
Somit beträgt das Durchschnittsalter der Bevölkerung für das Jahr 1950 genau  Jahre.
Prognosewert bestimmen
Der Prognosewert für das Jahr 2030 beträgt ungefähr
Jahre.
Prognosewert bestimmen
Der Prognosewert für das Jahr 2030 beträgt ungefähr  Jahre.
Jahre.
b)
Es ist das lokale Minimum des Graphen von  gesucht.
1. Schritt: Ableitung bestimmen
2. Schritt: Notwendige Bedingung für Extremstllen überprüfen
Mit der notwendigen Bedingung
gesucht.
1. Schritt: Ableitung bestimmen
2. Schritt: Notwendige Bedingung für Extremstllen überprüfen
Mit der notwendigen Bedingung  für eine lokale Extremstelle folgt:
Hierbei gilt, dass
für eine lokale Extremstelle folgt:
Hierbei gilt, dass  nicht in dem Intervall
nicht in dem Intervall ![\([0;80]\)](https://mathjax.schullv.de/fff53c079acd87232df98ea62e23d85afae9fdf09f6750a96b4591a522432aca?color=5a5a5a) liegt und somit keine Lösung sein kann.
3. Schritt: Vorzeichenwechsel-Kriterium anwenden
Daraus folgt, dass an der Stelle
liegt und somit keine Lösung sein kann.
3. Schritt: Vorzeichenwechsel-Kriterium anwenden
Daraus folgt, dass an der Stelle  ein lokales Minimum des Graphen von
ein lokales Minimum des Graphen von  vorliegt.
4. Schritt: Durschnittsalter bestimmen
Somit beträgt das niedrigste Durchschnittsalter der Bevölkerung im Zeitraum von 1950 bis 2030 ungefähr
vorliegt.
4. Schritt: Durschnittsalter bestimmen
Somit beträgt das niedrigste Durchschnittsalter der Bevölkerung im Zeitraum von 1950 bis 2030 ungefähr  Jahre.
Jahre.
c)
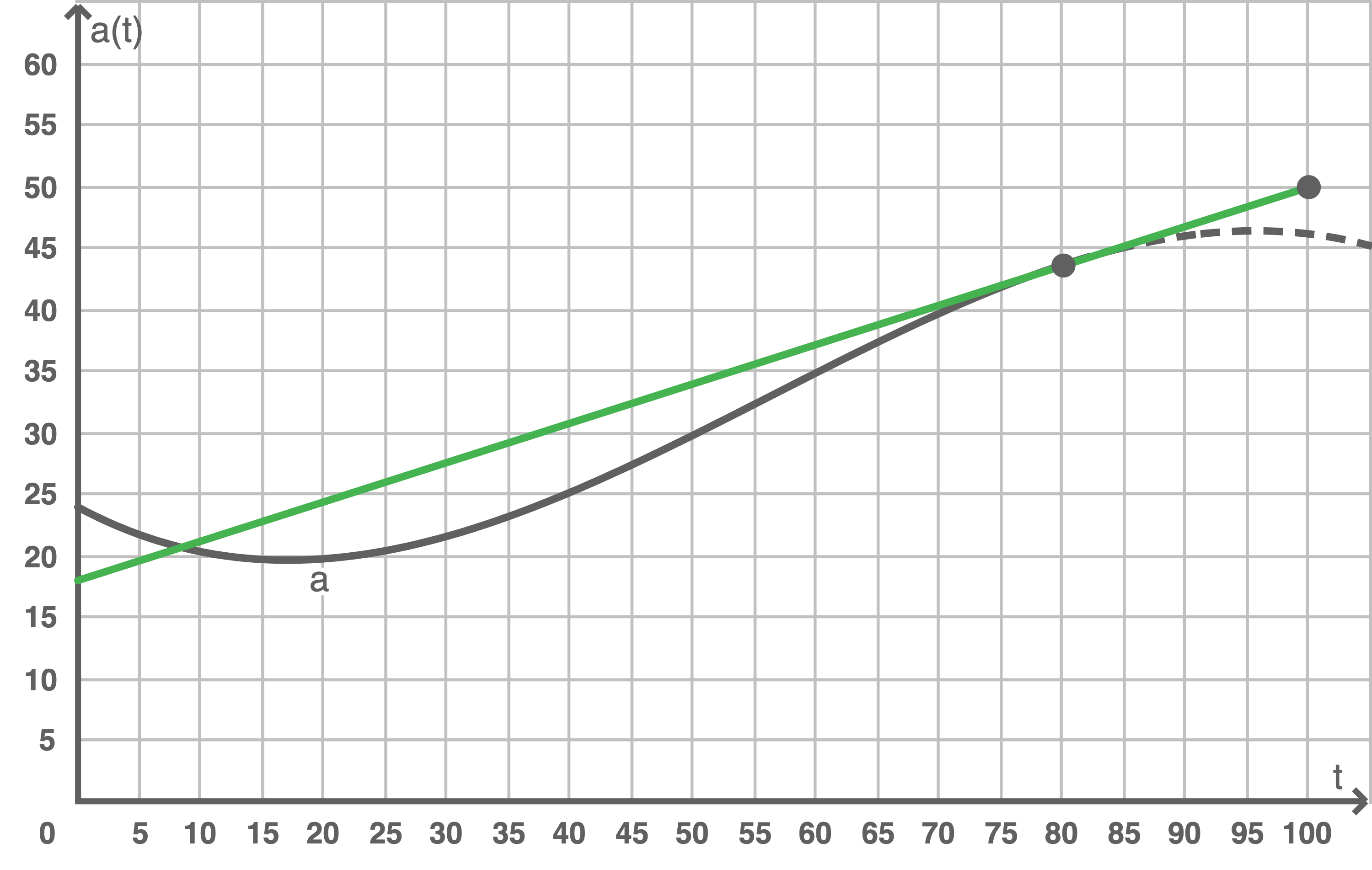
d)
(1)
Die Aussage ist falsch, da die Änderungsrate des Durchschnittsalters der Bevölkerung auch negative Funktionswerte annimmt und somit das Durchschnittsalter der Bevölkerung abnimmt.
(2)
Graph einzeichnen
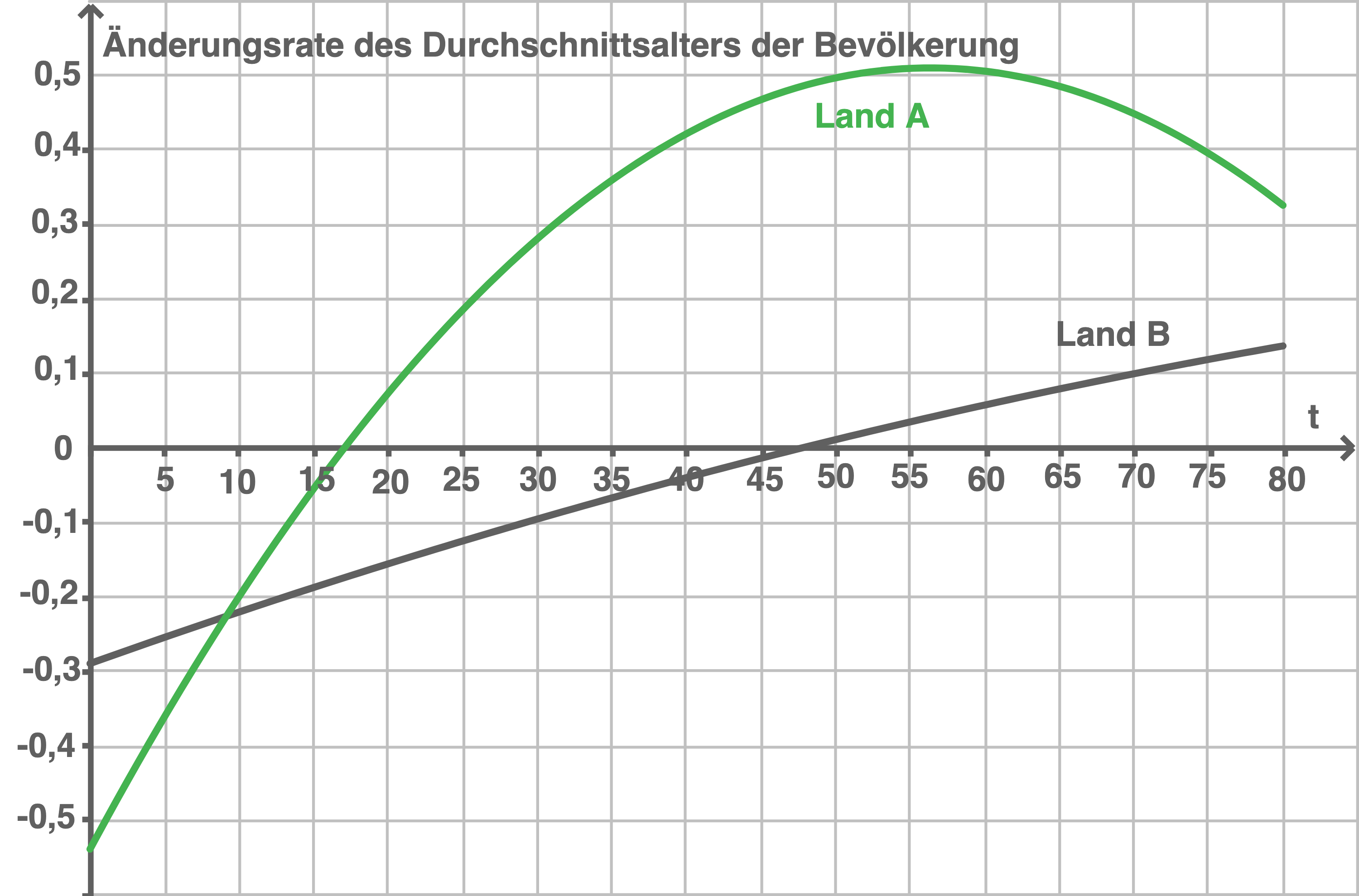 Bedeutung im Sachzusammenhang angeben
Die erste Ableitung einer Funktion beschreibt immer die momentane Änderungsrate der Funktionswerte. Durch
Bedeutung im Sachzusammenhang angeben
Die erste Ableitung einer Funktion beschreibt immer die momentane Änderungsrate der Funktionswerte. Durch  wird also die Änderungsrate des Durchschnittsalters der Bevölkerung von Land A zum Zeitpunkt
wird also die Änderungsrate des Durchschnittsalters der Bevölkerung von Land A zum Zeitpunkt  modelliert.
modelliert.

(3)
Die Aussage ist wahr, da die Änderungsrate des Durchschnittsalters der Bevölkerung im Jahr 2020 für das Land
für das Land  größer ist, als für das Land
größer ist, als für das Land 
© - SchulLV.
Lösung 3
a)
b)
1. Schritt: Ableitung bestimmen
Für die Ableitungsfunktion der Funktion  gilt:
gilt:
![\(\begin{array}[t]{rll}
f(x)&=& \dfrac{1}{4} \cdot x^4 -2 \cdot x^2 +2 \\[5pt]
f](https://mathjax.schullv.de/4098a2415bb2eb8552324484b419b9cd0fc8beb2d28f03189bf3e64944db7c37?color=5a5a5a) 2. Schritt: Notwendiges Kiterium für Extremstellen überprüfen
Mit dem notwendigen Kriterium
2. Schritt: Notwendiges Kiterium für Extremstellen überprüfen
Mit dem notwendigen Kriterium  für eine lokale Extremstelle folgt:
für eine lokale Extremstelle folgt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/a8a09c6e15156ffbb585aa2096fa547b2ca29499ef2d16206852d7f42991708e?color=5a5a5a) Mit dem Satz vom Nullprodukt gilt:
Mit dem Satz vom Nullprodukt gilt:
![\(\begin{array}[t]{rll}
x_1 &=& 0 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/829a78b1edda5611afc6f295dd5f9f7740ed55a447f77790abd51dd8710ede0b?color=5a5a5a)
![\(\begin{array}[t]{rll}
x^2-4 &=& 0 \quad \scriptsize \mid\; +4 \\[5pt]
x^2 &=& 4 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
x_2 &=& 2 \\[5pt]
x_3 &=& -2 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/1e946af257fb2953ca189d1678d7a78556de660f1c67720a20c3a4145721d816?color=5a5a5a) 3. Schritt: Vorzeichenwechsel-Kriterium anwenden
3. Schritt: Vorzeichenwechsel-Kriterium anwenden
![\(\begin{array}[t]{rll}
f‘(1)&=& 1^3 -4 \cdot 1 \\[5pt]
&=& -3 \quad \lt 0
\end{array}\)](https://mathjax.schullv.de/0233c3a13f06eaa5d0f16b17dcdbe96d8a9a465975cc7b1417947d1ba1eac199?color=5a5a5a)
![\(\begin{array}[t]{rll}
f‘(3)&=& 3^3 -4 \cdot 3 \\[5pt]
&=& 15 \quad \gt 0
\end{array}\)](https://mathjax.schullv.de/5d0ff76c674395024172bef38a70b4b5f363afa4754716841315fe667d5332ff?color=5a5a5a) Somit besitzt der Graph der Ableitungsfunktion an der Stelle
Somit besitzt der Graph der Ableitungsfunktion an der Stelle  einen Vorzeichenwechsel von negativen zu positiven Funktionswerten. Damit ist das hinreichende Kriterium für eine lokale Minimalstelle erfüllt und der Graph der Funktion
einen Vorzeichenwechsel von negativen zu positiven Funktionswerten. Damit ist das hinreichende Kriterium für eine lokale Minimalstelle erfüllt und der Graph der Funktion  besitzt an der Stelle
besitzt an der Stelle  eine lokale Minimalstelle.
eine lokale Minimalstelle.
c)
Es können beispielsweise die folgenden beiden Unterschiede genannt werden:
- Der Graph der Funktion
ist achsensymmetrisch zur
-Achse, wobei der Graph der Funktion
keine Symmetrie aufweist.
- Der Graph der Funktion
besitzt vier und der Graph der Funktion
insgesamt zwei Nullstellen.
d)
(1)

(2)
Für die gemeinsamen Punkte der Tangente  und dem Graphen der Funktion
und dem Graphen der Funktion  folgt durch Gleichsetzen der Funktionsgleichungen:
Dadurch besitzen die Tangente
folgt durch Gleichsetzen der Funktionsgleichungen:
Dadurch besitzen die Tangente  und der Graph der Funktion
und der Graph der Funktion  an den Stellen
an den Stellen  und
und  einen gemeinsamen Punkt.
Für eine Tangente an der Stelle
einen gemeinsamen Punkt.
Für eine Tangente an der Stelle  muss außerdem gelten, dass die Steigung der Tangente gleich der Steigung von
muss außerdem gelten, dass die Steigung der Tangente gleich der Steigung von  an der Stelle
an der Stelle  ist. Für die Ableitungsfunktion der Funktion
ist. Für die Ableitungsfunktion der Funktion  folgt:
folgt:
![\(\begin{array}[t]{rll}
g(x)&=& \dfrac{1}{4} \cdot x^4 -2 \cdot x^2 - \dfrac{3}{2} \cdot x +2 \\[5pt]
g](https://mathjax.schullv.de/55cac8dca3d0b11ccf612c99f9d1d1966d4390029b94fde20f7161eab30573f4?color=5a5a5a) Damit folgt für
Damit folgt für  :
:
![\(\begin{array}[t]{rll}
g](https://mathjax.schullv.de/8d3291f96311ca68f612aca7a240c5f276a54e5d0ba217379d732449b64a5b7b?color=5a5a5a) Somit gilt, dass die Steigung des Graphen von
Somit gilt, dass die Steigung des Graphen von  an der Stelle
an der Stelle  gleich der Steigung der Tangente ist. Deshalb ist die Tangente
gleich der Steigung der Tangente ist. Deshalb ist die Tangente  in dem Punkt
in dem Punkt  auch eine Tangente an den Graphen von
auch eine Tangente an den Graphen von 
e)
Die Steigung der Tangente ist durch  gegeben. Da der Graph der Funktion
gegeben. Da der Graph der Funktion  um
um  Einheiten nach rechts verschoben wird, muss er um
Einheiten nach rechts verschoben wird, muss er um  Einheiten nach unten verschoben werden, damit die Verschiebung entlang der Tangente verläuft.
Einheiten nach unten verschoben werden, damit die Verschiebung entlang der Tangente verläuft.
Lösung 4
a)
Durchschnittsalter bestimmen
Somit beträgt das Durchschnittsalter der Bevölkerung für das Jahr 1950 genau  Jahre.
Prognosewert bestimmen
Der Prognosewert für das Jahr 2030 beträgt ungefähr
Jahre.
Prognosewert bestimmen
Der Prognosewert für das Jahr 2030 beträgt ungefähr  Jahre.
Jahre.
b)
Es ist das lokale Minimum des Graphen von  gesucht.
1. Schritt: Ableitung bestimmen
2. Schritt: Notwendige Bedingung für Extremstllen überprüfen
Mit der notwendigen Bedingung
gesucht.
1. Schritt: Ableitung bestimmen
2. Schritt: Notwendige Bedingung für Extremstllen überprüfen
Mit der notwendigen Bedingung  für eine lokale Extremstelle folgt:
Hierbei gilt, dass
für eine lokale Extremstelle folgt:
Hierbei gilt, dass  nicht in dem Intervall
nicht in dem Intervall ![\([0;80]\)](https://mathjax.schullv.de/fff53c079acd87232df98ea62e23d85afae9fdf09f6750a96b4591a522432aca?color=5a5a5a) liegt und somit keine Lösung sein kann.
3. Schritt: Vorzeichenwechsel-Kriterium anwenden
Daraus folgt, dass an der Stelle
liegt und somit keine Lösung sein kann.
3. Schritt: Vorzeichenwechsel-Kriterium anwenden
Daraus folgt, dass an der Stelle  ein lokales Minimum des Graphen von
ein lokales Minimum des Graphen von  vorliegt.
4. Schritt: Durschnittsalter bestimmen
Somit beträgt das niedrigste Durchschnittsalter der Bevölkerung im Zeitraum von 1950 bis 2030 ungefähr
vorliegt.
4. Schritt: Durschnittsalter bestimmen
Somit beträgt das niedrigste Durchschnittsalter der Bevölkerung im Zeitraum von 1950 bis 2030 ungefähr  Jahre.
Jahre.
c)

d)
(1)
Die Aussage ist falsch, da die Änderungsrate des Durchschnittsalters der Bevölkerung auch negative Funktionswerte annimmt und somit das Durchschnittsalter der Bevölkerung abnimmt.
(2)
Graph einzeichnen
 Bedeutung im Sachzusammenhang angeben
Die erste Ableitung einer Funktion beschreibt immer die momentane Änderungsrate der Funktionswerte. Durch
Bedeutung im Sachzusammenhang angeben
Die erste Ableitung einer Funktion beschreibt immer die momentane Änderungsrate der Funktionswerte. Durch  wird also die Änderungsrate des Durchschnittsalters der Bevölkerung von Land A zum Zeitpunkt
wird also die Änderungsrate des Durchschnittsalters der Bevölkerung von Land A zum Zeitpunkt  modelliert.
modelliert.

(3)
Die Aussage ist wahr, da die Änderungsrate des Durchschnittsalters der Bevölkerung im Jahr 2020 für das Land
für das Land  größer ist, als für das Land
größer ist, als für das Land 
© 2017 - SchulLV.
© 2017 - SchulLV.
© 2017 - SchulLV.
© 2017 - SchulLV.

