Exponentialfunktion zur Basis 2
Definition
Eine Exponentialfunktion ist eine Funktion, deren Variable
im Exponenten steht.
Die Exponentialfunktion zur Basis 2 hat die Funktionsgleichung 
und den Definitionsbereich 
Die Basis zeigt an, wie steil die Kurve verläuft. Für die Basis 2 gilt, dass sich der Funktionswert mit jedem Schritt verdoppelt.
Eigenschaften
- Der Funktionsgraph ist steigend.
- Der Wertebereich umfasst alle positiven reellen Zahlen:
Für
ist 
Für
ist 
Für
ist 
- Der Graph schneidet die
-Achse im Punkt 
- Der Graph nähert sich dem negativen Abschnitt der -Achse an.
- Die Funktion hat keine Nullstelle.
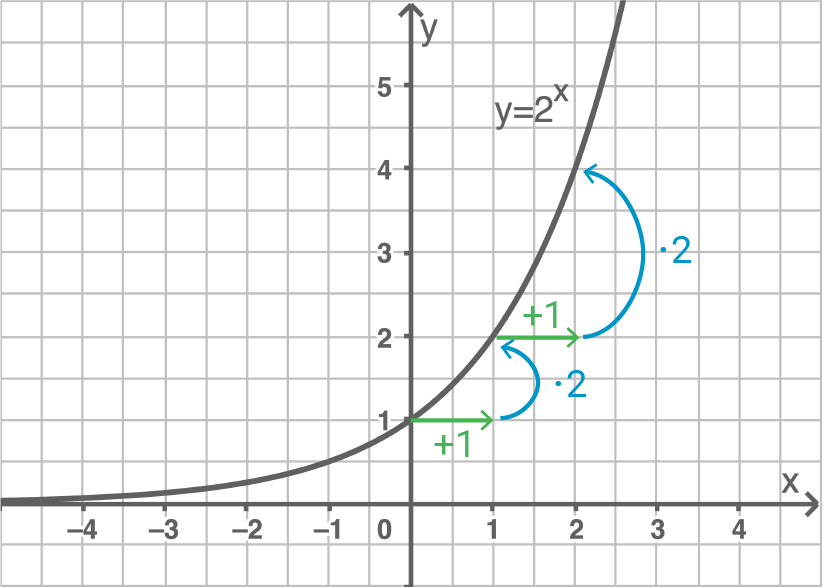
- Wenn um 1 wächst, so wird der Funktionswert
mit 2 multipliziert.
1
Eine Bakterienkultur hat eine Verdopplungszeit von einer Stunde. Zu Beginn nimmt die Kultur eine Fläche von 
ein.
ein.
a)
Beschreibe das Wachstum der Kultur.
b)
Erstelle eine Wertetabelle. Wie groß ist die von der Kultur bedeckte Fläche nach 8 Stunden?
2
Wie verändert sich jedes Mal der Funktionswert der Funktion mit 
, wenn man ...
, wenn man ...
a)
... um 3 vergrößert.
b)
... um 0,5 vergrößert.
c)
... um 2 verkleinert.
d)
...verdoppelt.
e)
...halbiert.
f)
...viertelt.
Weiter lernen mit SchulLV Plus!
monatlich kündbarSchulLV Plus-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Die Bakterienkultur wächst exponentiell mit der Funktionsgleichung 
b)
Zeit  in Stunden |
Fläche  in  |
|---|---|
 |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
2
a)
Der Funktionswert wird um das 
-fache, also um das 8-fache, vergrößert.
-fache, also um das 8-fache, vergrößert.
b)
Der Funktionswert wird mit 
multipliziert.
multipliziert.
c)
Der Funktionswert wird um das 
-fache kleiner, also um den Faktor 4. Er wird somit auf ein Viertel des ursprünglichen Werts verringert.
-fache kleiner, also um den Faktor 4. Er wird somit auf ein Viertel des ursprünglichen Werts verringert.
d)
Es gilt 
der Funktionswert wird also quadriert.
der Funktionswert wird also quadriert.
e)
Wird halbiert, so muss der Exponent von halbiert werden. Der Funktionswert ist dann also 
Aus dem Funktionswert wird also die Wurzel gezogen.
halbiert, so muss der Exponent von halbiert werden. Der Funktionswert ist dann also Aus dem Funktionswert wird also die Wurzel gezogen.
f)
Wird geviertelt, so muss der Exponent von geviertelt werden. Der Funktionswert ist dann also ![\(2^{\frac{1}{4}x}=(2^x)^{\frac{1}{4}}=\sqrt[4]{2^x}.\)](https://www.schullv.de/resources/formulas/36cceb726f844522c3e64ffe5764d8186400c8e282a76bfcc677e2fc7cf4fd47_light.svg)
Aus dem Funktionswert wird also die vierte Wurzel gezogen.
geviertelt, so muss der Exponent von geviertelt werden. Der Funktionswert ist dann also Aus dem Funktionswert wird also die vierte Wurzel gezogen.