Teil B

Betrachtet wird die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^2-4 \cdot x+3.$

1.1

Gib die Nullstellen von $f$ an.
Gib die Koordinaten des Schnittpunkts des Graphen von $f$ mit der $y$ -Achse an.

(2 BE)

1.2

Ermittle den Wertebereich von $f$ .

(2 BE)

1.3

Die Graphen von $f$ und der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=-\dfrac{1}{3} \cdot(x-4)^2+3$ schneiden sich in den Punkten $A$ und $B$ .
Ermittle eine Gleichung der linearen Funktion, deren Graph durch die Punkte $A$ und $B$ verläuft.

(4 BE)

Matteo macht eine Fahrt mit seinem Segelboot.

2.1

Das Segelboot fährt auf einem geradlinigen Kurs, der durch die Punkte $A$ und $B$ verläuft. Im Punkt $L$ befindet sich ein Leuchtturm (siehe Abbildung).

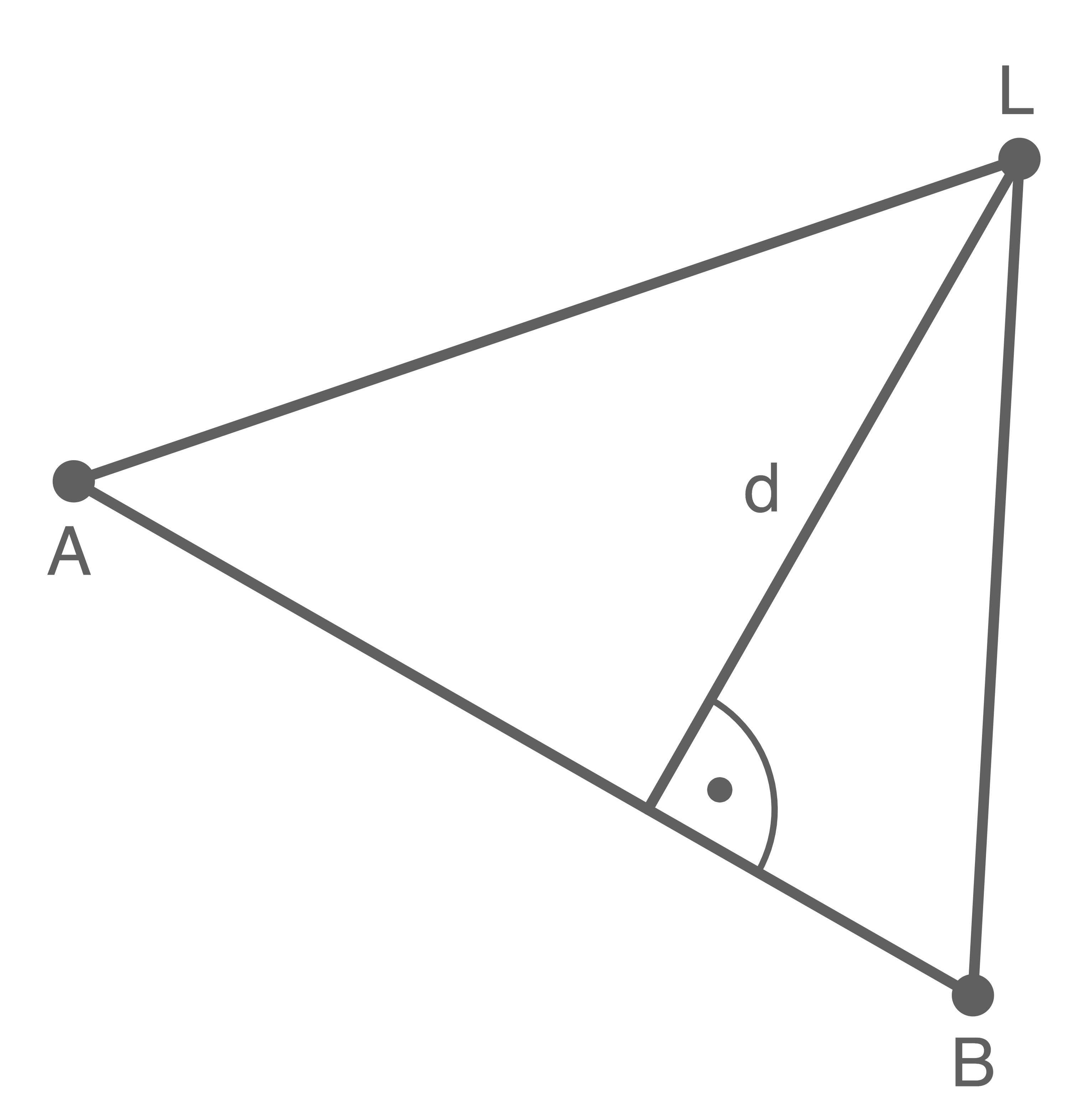Es gilt: $\sphericalangle B A L=46,3^{\circ},$ $\sphericalangle L B A=61,4^{\circ},$ $\overline{A B}=1,45 \mathrm{~km}$

Die kürzeste Entfernung vom Leuchtturm zum Kurs des Segelbootes ist $d$ .
Berechne $d$ .

(5 BE)

2.2

Bei Windstille unterbricht Matteo seine Fahrt mit dem Segelboot und spielt mit einer quaderförmigen Streichholzschachtel.
Er wirft die Streichholzschachtel 60-mal und zählt, wie oft sie auf eine der beiden kleinsten, auf eine der beiden mittleren oder auf eine der beiden größten Seitenflächen fällt.
In einer Tabelle hat er seine berechneten relativen Häufigkeiten zusammengefasst.

Seitenflächen	kleinste	mittlere	größte
relative Häufigkeit	$\dfrac{4}{15}$	$\dfrac{7}{20}$	$\dfrac{2}{5}$

Begründe, dass seine Berechnungen fehlerhaft sind.

(2 BE)

Der Leipziger Schaustellerverein organisierte einen Jahrmarkt.
Eine Drohne überfliegt diesen Jahrmarkt und macht dabei Film- und Fotoaufnahmen.
Der Flug der Drohne wird in einem Koordinatensystem (1 Längeneinheit entspricht 1 Meter) näherungsweise durch den Graphen der Funktion $f$ mit $y=f(x)=50 \cdot \sin (0,08 \cdot x-20)+65 \quad$ $(x \in \mathbb{R}, 0 \leq x \leq 250)$ dargestellt.

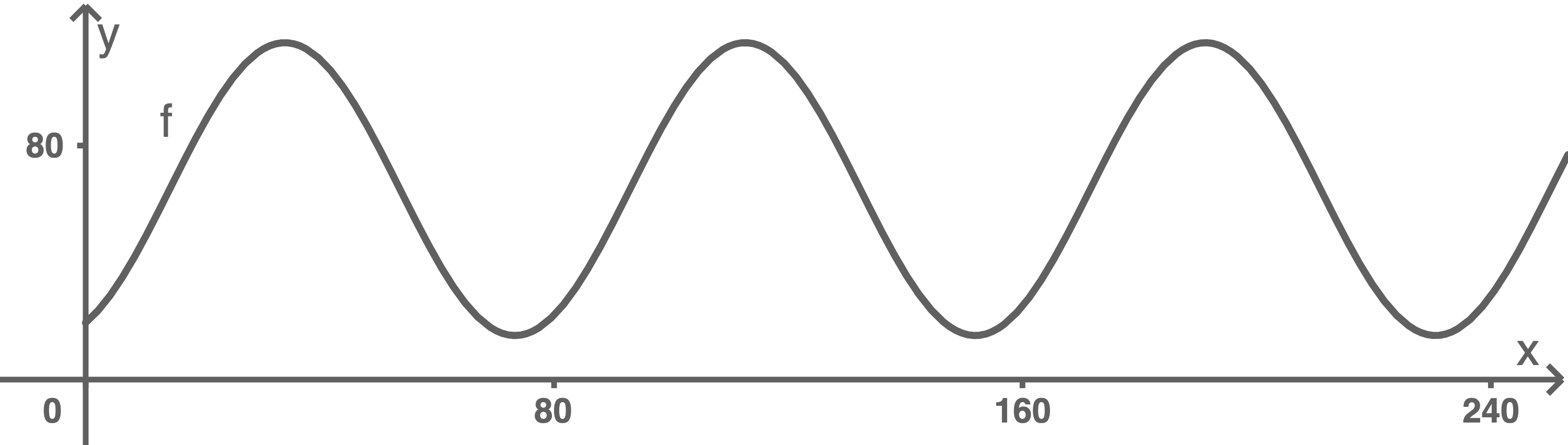Dabei gibt $x$ die horizontale Entfernung vom Eingangstor des Jahrmarkts und $y$ die jeweilige Höhe der Drohne über dem ebenen Boden an.

3.1

Ermittle die Höhe der Drohne über dem ebenen Boden am Eingangstor.
Bestimme die horizontale Entfernung vom Eingangstor, an der die Drohne auf ihrem Flug zum zweiten Mal eine Höhe von $50 \,\text{m}$ über dem Boden erreicht.

(4 BE)

3.2

Für Drohnenflüge über Menschen ist eine Minimalhöhe von $10 \,\text{m}$ und eine Maximalhöhe von $120 \,\text{m}$ über dem Boden festgelegt.
Zeige, dass beide Bedingungen während des gesamten Flugs der Drohne über den Jahrmarkt eingehalten werden.

(4 BE)

3.3

Auf dem Jahrmarkt gibt es ein Riesenrad.
Der äußere kreisförmige Ring des Riesenrades hat einen Durchmesser von $38,2 \,\text{m}.$ An diesem sind 36 Gondeln befestigt. Der Abstand benachbarter Befestigungspunkte ist gleich groß.
Ermittle die Länge des Bogens zwischen den Befestigungspunkten benachbarter Gondeln.

(3 BE)

3.4

Der Freifallturm ist eine der Hauptattraktionen des Jahrmarkts. Im Koordinatensystem wird der Freifallturm durch die Strecke $\overline{F S}$ mit $F(190 \mid 0)$ und $S(190 \mid 40)$ beschrieben.
Die Kamera der Drohne soll vom Punkt $K(236 \mid 20)$ aus Fotos vom Freifallturm aufnehmen. Der Öffnungswinkel des Objektivs der Kamera beträgt $40^{\circ}.$

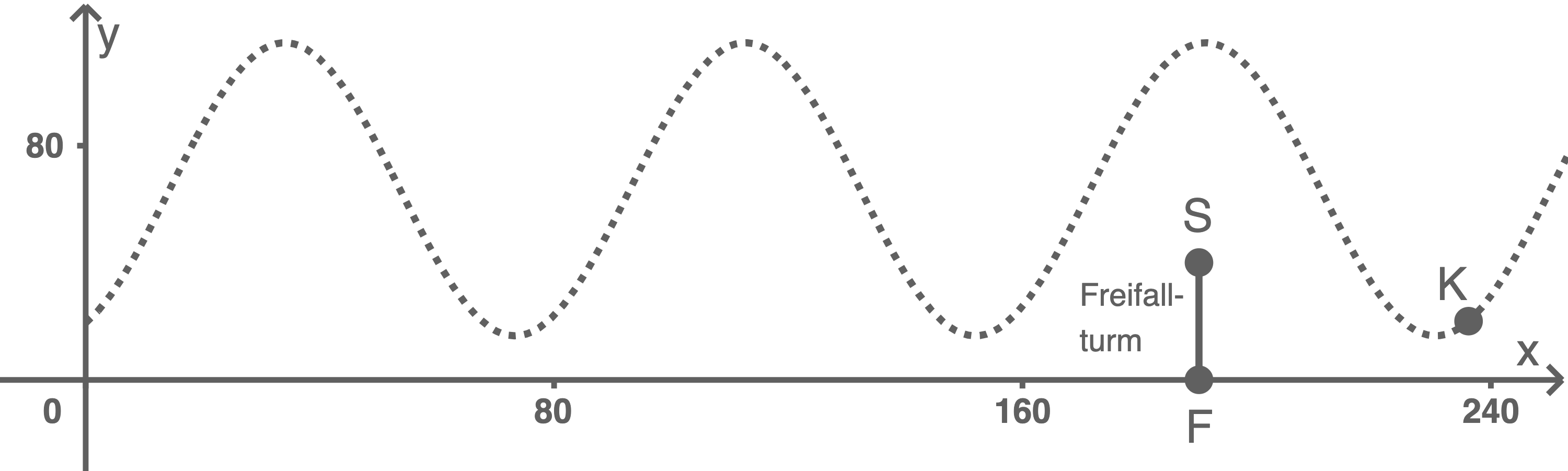Untersuche, ob die Kamera von $K$ aus ein Foto aufnehmen kann, auf dem der Freifallturm in voller Höhe sichtbar ist.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Nullstellen

Der Taschenrechner liefert die Nullstellen $x_1=1$ und $x_2=3.$

Koordinaten des Schnittpunkts mit der y-Achse

$f(0)=3$

Daraus folgt für den Schnittpunkt der Funktion $f$ mit der $y$ -Achse:

$S(0\mid 3)$

1.2

Der Graph der Funktion ist eine nach oben geöffnete Parabel mit dem Tiefpunkt $(2\mid -1).$ Dadurch ergibt sich der folgende Wertebereich:

$W=\{y\mid y\in \mathbb R, y\geq -1\}$

1.3

Schnittpunkte bestimmen

Gesucht ist die Lösung der Gleichung $f(x)=g(x).$

Der Taschenrechner liefert die Lösungen $x_A=1$ und $x_B=4.$

$f(1)=0$

$f(4)=3$

Die Schnittpunkte haben die Koordinaten $A(1\mid 0)$ und $B(4\mid 3).$

Gleichung der Funktion ermitteln

Die lineare Funktion hat die allgemeine Funktionsgleichung $y=m\cdot x+n.$

$m=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{3-0}{4-1}=1$

$m=1$ und Koordinaten von $A$ in die allgemeine Funktionsgleichung einsetzen:

$\begin{array}[t]{rll} 0&=& 1\cdot 1+n &\quad \scriptsize \mid\; -1 \\[5pt] -1&=& n \end{array}$

Insgesamt ergibt sich damit die lineare Funktionsgleichung:

$y=x-1$

2.1

$\sphericalangle ALB=180°-61,4°-46,3°=72,3°$

Mit dem Sinussatz folgt für die Länge der Strecke $\overline{AL}:$

$\begin{array}[t]{rll} \dfrac{\overline{AL}}{\sin(\sphericalangle LBA)}&=& \dfrac{\overline{AB}}{\sin(\sphericalangle ALB)} \\[5pt] \dfrac{\overline{AL}}{\sin(61,4°)}&=& \dfrac{1,45\,\text{km}}{\sin(72,3°)} \quad \scriptsize \mid\; \cdot \sin(61,4°)\\[5pt] \overline{AL}&=& \dfrac{1,45\,\text{km}}{\sin(72,3°)}\cdot \sin(61,4°) \\[5pt] \overline{AL}&\approx& 1,34\,\text{km} \end{array}$

Daraus folgt für den Abstand $d:$

$\begin{array}[t]{rll} \cos(\sphericalangle BAL)&=& \dfrac{d}{\overline{AL}} \quad \scriptsize \mid\; \cdot \overline{AL} \\[5pt] \cos(\sphericalangle BAL)\cdot \overline{AL}&=& d \\[5pt] \cos(46,3°)\cdot 1,34\,\text{km}&=& d \\[5pt] 0,93\,\text{km}&\approx& d \end{array}$

Die kürzeste Entfernung vom Leuchtturm zum Kurs beträgt ungefähr $0,93\,\text{km}.$

2.2

$\dfrac{4}{15}+\dfrac{7}{20}+\dfrac{2}{5}=\dfrac{16}{60}+\dfrac{21}{60}+\dfrac{24}{60}=\dfrac{61}{60}$

Die Summe aller relativen Häufigkeiten muss $1$ ergeben. Da dies hier nicht der Fall ist, müssen Matteos Berechnungen fehlerhaft sein.

3.1

Höhe der Drohne am Eingangstor

Der Taschenrechner liefert:

$f(0)\approx 19,35$

Die Höhe der Drohne am Eingangstor beträgt ungefähr $19,35\,\text{m}.$

Horizontale Entfernung berechnen

Gesucht ist der zweite Wert größer $0,$ für den $f(x)=50$ gilt.

Der Taschenrechner liefert:

$x_1\approx 10,57\quad x_2\approx57,46$

Die Drohne erreicht in einer horizontalen Entfernung von ungefähr $57,46\,\text{m}$ zum zweiten Mal eine Höhe von $50\,\text{m}.$

3.2

Die Sinusfunktion nimmt nur Werte zwischen $1$ und $-1$ an. Der größte Wert der Funktion wird also für den Sinuswert $1$ erzielt:

$50\cdot 1+65=115$

Die Drohne fliegt folglich maximal $115\,\text{m}$ hoch. Der niedrigste Wert der Funktion wird für den Sinuswert $-1$ erzielt:

$50\cdot (-1)+65=15$

Die Drohne fliegt also minimal $15\,\text{m}$ hoch.

Damit werden beide Bedingungen während des gesamten Flugs der Drohne über den Jahrmarkt eingehalten.

3.3

Umfang des kreisförmigen Rings des Riesenrads:

$U=\pi\cdot d=\pi\cdot 38,2\,\text{m}\approx 120\,\text{m}$

Da die Bögen zwischen den Befestigungspunkten in 36 gleich große Abschnitte eingeteilt sind, gilt für die Länge eines Bogens:

$\dfrac{120\,\text{m}}{36}\approx 3,33\,\text{m}$

Die Länge des Bogens zwischen zwei benachbarten Gondeln beträgt ungefähr $3,33\,\text{m}.$

3.4

Höhe des Freifallturms: $y_S-y_F=40-0=40[\text{m}]$

Entfernung der Kamera: $x_K-x_S=236-190=46[\text{m}]$

Skizze

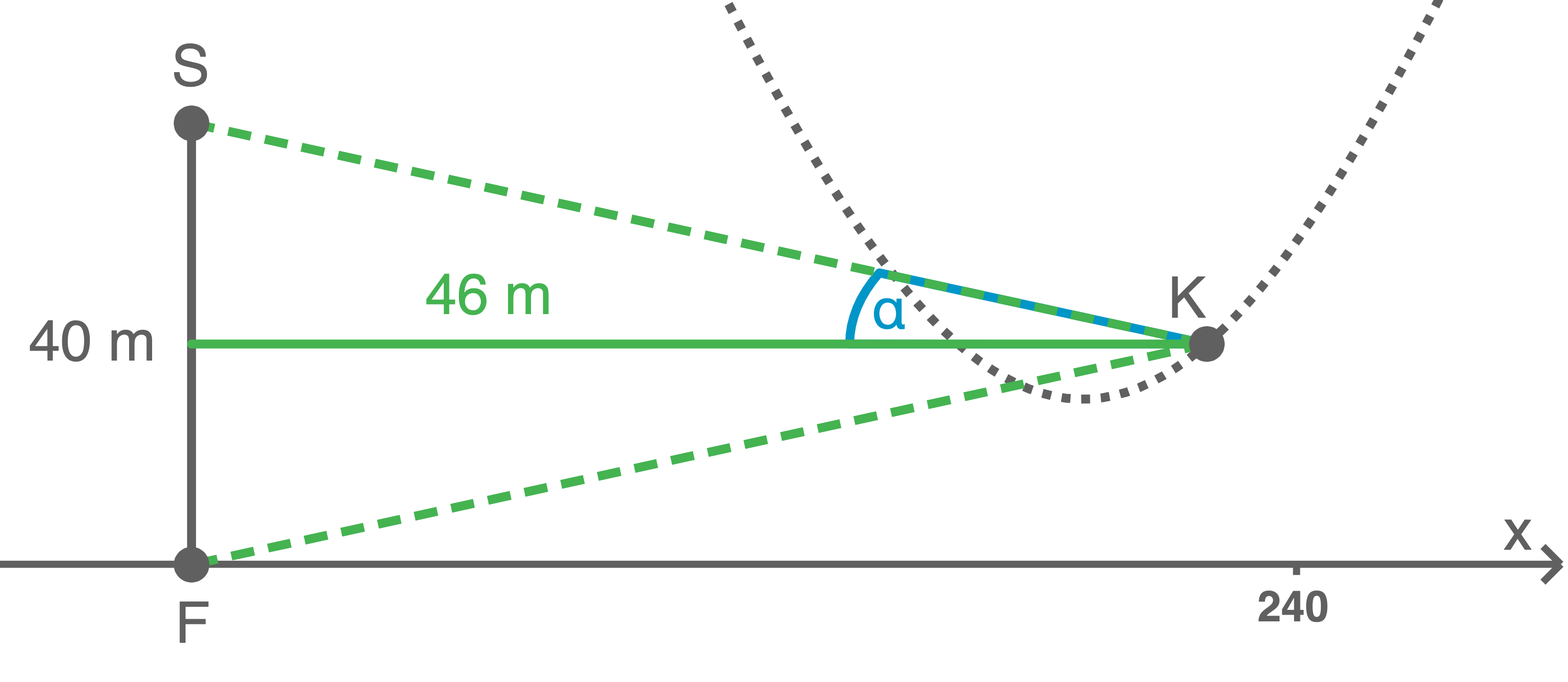Für den Winkel $\alpha$ gilt:

$\begin{array}[t]{rll} \tan(\alpha)&=& \dfrac{20\,\text{m}}{46\,\text{m}} \quad \scriptsize \mid\; \tan^{-1} \\[5pt] \alpha&=& \tan^{-1}\left(\dfrac{20}{46}\right) \\[5pt] \alpha &\approx& 23,5° \end{array}$

Damit die Kamera den Freifallturm in voller Höhe aufnehmen kann, müsste der Öffnungswinkel des Objektivs mindestens $2\cdot \alpha=47°$ betragen.

Die Kamera kann kein Foto aufnehmen, auf dem der Freifallturm in voller Höhe sichtbar ist.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?