Teil B

Gegeben sind die Funktionen $f$ und $g$ durch
$y=f(x) = 3^x\quad (x\in\mathbb{R})\quad$ und $\quad y=g(x) = 3^{x+1}\quad (x\in\mathbb{R}).$

1.1

Gib den Wertebereich der Funktion $f$ an.

Gib die Koordinaten des Schnittpunkts des Graphen von $f$ mit der $y$ -Achse an.

(3 BE)

1.2

Der Punkt $A\left(x_A\mid \frac{1}{81}\right)$ liegt auf dem Graphen von $g.$

Ermittle die Koordinate $x_A.$

(2 BE)

1.3

Der Graph von $f$ schneidet die $y$ -Achse im Punkt $P,$ der Graph von $g$ schneidet die $y$ -Achse im Punkt $Q.$
Die Punkte $P,$ $B(2\mid 0)$ und $Q$ bilden ein Dreieck.

Bestimme den Flächeninhalt des Dreiecks $PBQ.$

(3 BE)

In Radebeul findet jährlich der „Sächsische Mount Everest Treppenmarathon“ statt.

2.1

Die Siegerzeiten der männlichen Teilnehmer in der Startklasse „Alleingang“ sind für die Jahre 2011 bis 2015 in folgender Tabelle dargestellt:

Jahr	2011	2012	2013	2014	2015
Zeit in h	14,94	13,79	14,77	13,45	13,77

Berechne das arithmetische Mittel der Siegerzeiten der Jahre 2011 bis 2015.

(2 BE)

2.2

In der Startklasse „Dreierseilschaft“ starten drei Teilnehmer als Mannschaft.

Gib die Anzahl aller möglichen Reihenfolgen an, in der die drei Teilnehmer einer Dreierseilschaft starten können.

(1 BE)

2.3

Der Treppenlauf hat verschiedene Abschnitte.
Die geradlinige Laufstrecke im Abschnitt „Spitzhaustreppe“ besitzt einen konstanten Anstieg. Auf einer Karte im Maßstab 1:10 000 ist dieser Abschnitt 1,9 cm lang. Der Höhenunterschied zwischen Anfang und Ende dieses Abschnitts beträgt 73,4 m.

Berechne die Länge der geradlinigen Laufstrecke im Abschnitt „Spitzhaustreppe".

(3 BE)

Windkraftanlagen haben bei der Erzeugung von Elektroenergie große Bedeutung.

3.1

Der Turm einer Windkraftanlage hat die Form eines Kreiszylinders.
Der Turm ist 72,20 m hoch und besitzt einen Durchmesser von 3,70 m.
Die Mantelfläche des Turms soll einen neuen Schutzanstrich erhalten. Für diesen Schutzanstrich werden pro Quadratmeter 0,5 Liter Farbe benötigt.

Berechne, wie viele Liter Farbe für den Schutzanstrich benötigt werden.

(3 BE)

3.2

In der Nähe einer Autobahn befindet sich im Punkt $W$ eine Windkraftanlage (siehe Abbildung).

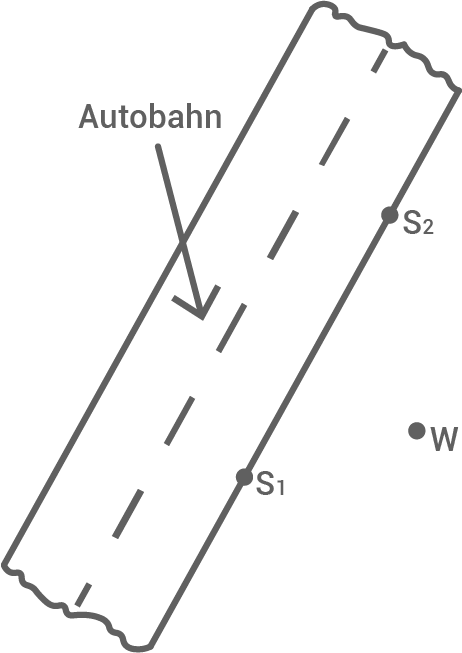
Abbildung (nicht maßstäblich)

Gesetzliche Regelungen schreiben für Windkraftanlagen einen Mindestabstand von 100 m zum Fahrbahnrand an Autobahnen vor.
Zur Überprüfung dieses Mindestabstands werden am Fahrbahnrand der Autobahn die Strecke $\overline{S_1S_2}$ abgesteckt und die Winkel $\sphericalangle WS_1S_2$ sowie $\sphericalangle S_1S_2W$ gemessen. Die Messwerte betragen:
$\overline{S_1S_2} = 350\,\text{m};$ $\sphericalangle WS_1S_2=32^°;$ $\sphericalangle S_1S_2W = 39^°$ .

Weise rechnerisch nach, dass gilt: $\overline{S_1W}= 233\,\text{m}.$

Zeige rechnerisch, dass der gesetzlich vorgegebene Mindestabstand eingehalten wurde.

(5 BE)

3.3

Die von einer Windkraftanlage abgegebene elektrische Leistung wurde über 12 Stunden hinweg gemessen und kann durch die Funktion $P$ mit
$P(t)=-11\cdot t^2 + 160\cdot t + 765$ $(t\in\mathbb{R},0\leq t \leq 12)$
beschrieben werden.

Dabei gilt:

$t\quad \;\;\;\;\;...$	Zeit nach Beginn der Messung in Stunden
$P(t)\;\;\; ...$	elektrische Leistung zur Zeit $t$ in Kilowatt

3.3.1

Bestimme, zu welcher Zeit $t$ die Windkraftanlage eine elektrische Leistung von genau $1\,000$ Kilowatt abgab.

(2 BE)

3.3.2

Ermittle die größte elektrische Leistung, die von der Windkraftanlage abgegeben wurde.

(2 BE)

3.3.3

Für eine bestimmte Zeit $t_1$ im Intervall $0\leq t_1 \leq 10$ gilt:
Die von der Windkraftanlage abgegebene elektrische Leistung steigt ab der Zeit $t_1$ in den darauffolgenden 2 Stunden um genau 100 Kilowatt.

Bestimme die Zeil $t_1.$

(2 BE)

3.4

Messungen an einer Windkraftanlage ergaben, dass diese Windkraftanlage während 18,4 % ihrer Gesamtbetriebszeit abgeschaltet werden musste.

Die Gründe für das Abschalten dieser Windkraftanlage sind in folgender Tabelle angegeben:

Grund für die Abschaltung	Anteil in Prozent
zu starker Wind	14,0
zu schwacher Wind	47,0
sonstige Gründe	39,0

Ermittle, während wie viel Prozent ihrer Gesamtbetriebszeit die Windkraftanlage wegen zu schwachen Windes abgeschaltet werden musste.

(2P)

1.1

Wertebereich angeben

Die Funktion $f(x)=3^x$ ist eine Exponentialfunktion mit positiver Basis $a=3.$ Nach Definition nimmt diese nur Werte größer als $0$ an.

Wertebereich: $y \in R, y\gt 0$

Schnittpunkt mit y-Achse angeben

$f(0)=3^0=1$

Schnittpunkt mit der $y$ -Achse: $P(0\mid 1)$

1.2

Gesucht ist die Lösung der Gleichung $\dfrac {1}{81}=3^{x_A+1}$ . Diese kann man mit dem CAS berechnet werden, indem der Schnittpunkt von $g$ mit der Geraden $a=\dfrac{1}{81}$ bestimmt wird.

menu $\rightarrow$ 6: Graph analysieren $\rightarrow$ 4: Schnittpunkt

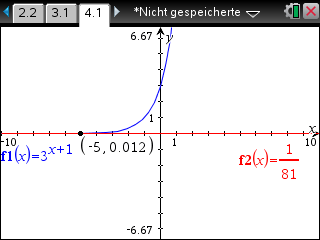Diagramm mit zwei Funktionen, eine in Blau und eine in Rot, auf einem Koordinatensystem dargestellt.

Die Koordinate $x_a$ hat den Wert $-5.$

1.3

$g(0)=3^{0+1}=3$

Damit folgt $Q(0\mid 3).$ Die Koordinaten des Punkts $P(0\mid 1)$ sind aus Aufgabe 1.1 bekannt.

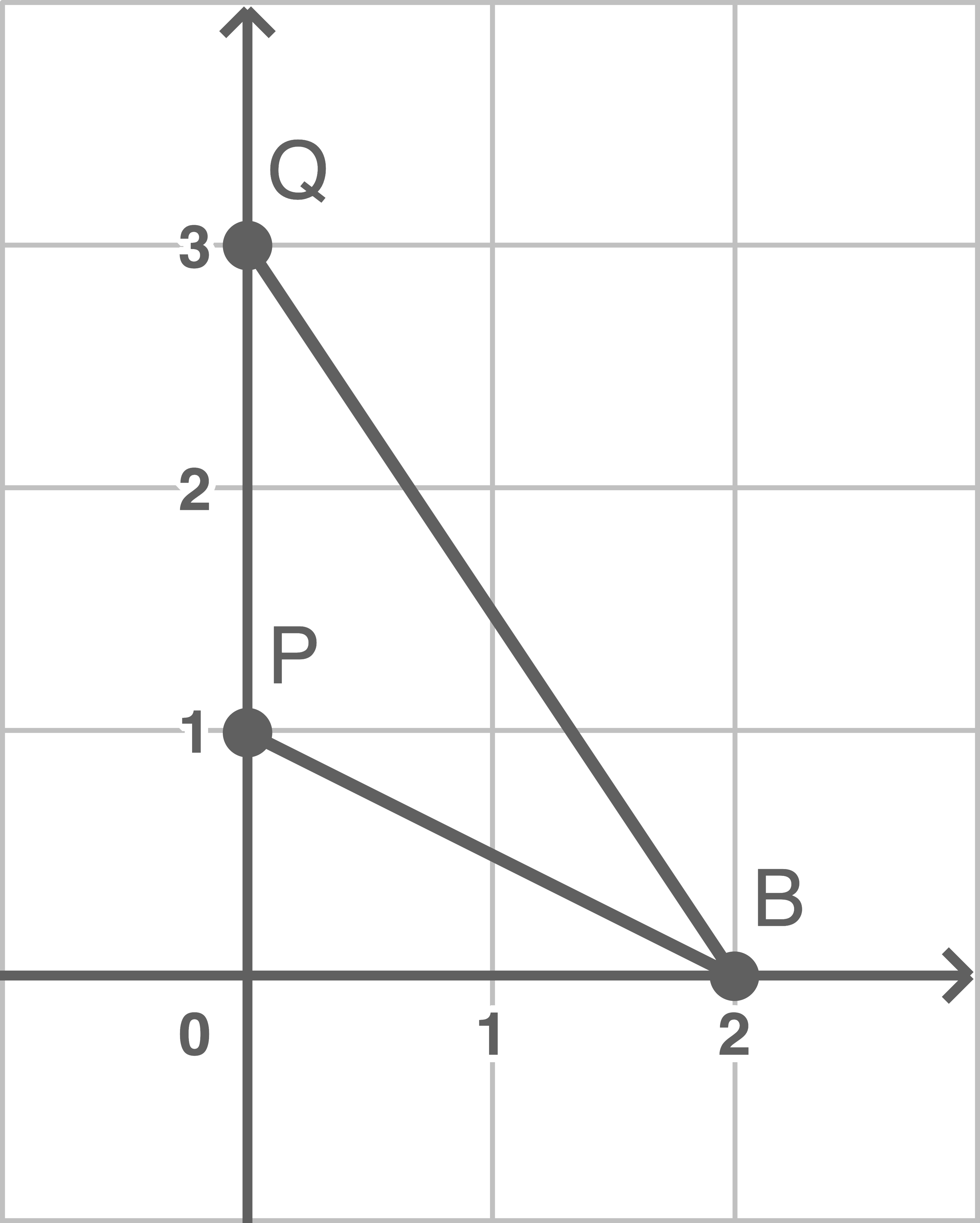
Skizze des Sachverhalts

Der Flächeninhalt eines Dreiecks lässt sich mit der Formel $A=\dfrac{1}{2}\cdot g\cdot h$ berechnen. Hier gilt:

$g=\overline{PQ}=2$
$h=\overline{OB}=2$

$A=\dfrac{1}{2}\cdot 2\cdot 2=2$

Der Flächeninhalt des Dreiecks $PBQ$ beträgt 2.

2.1

Rechenweg anzeigen

$E=14,144\,\text{h}$

Das arithmetische Mittel der Siegerzeiten beträgt $14,144 \mathrm{~h}.$

2.2

$n=3\cdot 2\cdot 1=6$

Es gibt 6 mögliche Startreihenfolgen.

2.3

Auf einer Karte im Maßstab $1:10\,000$ ist der Abschnitt des konstanten Anstiegs $1,9\,\text{cm}$ lang. Das heißt, dass dieser Abschnitt in der Realität

$1,9\,\text{cm}\cdot 10\,000=19\,000\text{cm}=190\,\text{m}$

lang ist.

Der Sachverhalt lässt sich wie folgt darstellen:

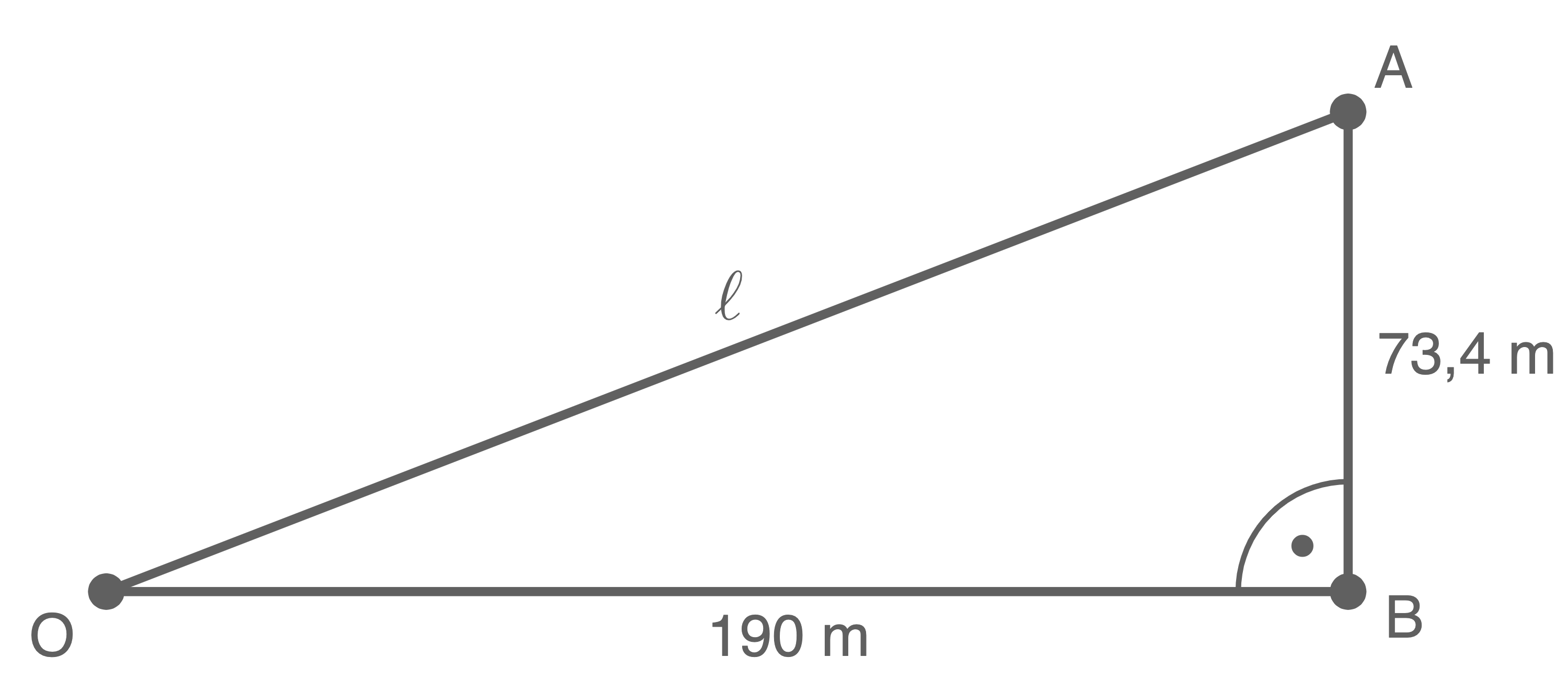Mit dem Satz des Pythagoras lässt sich nun die Läange $\ell$ der Laufstrecke berechnen:

$\begin{array}[t]{rll} \ell^2&=& (190\,\text{m})^2+(73,4\,\text{m})^2 \\[5pt] \ell^2&=& 41\,487,56 \,\text{m}^2 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt] \ell&\approx& 204\,\text{m} \end{array}$

Die Länge der Laufstrecke beträgt ungefähr 204 Meter.

3.1

Die Mantelfläche eines Zylinders lässt sich mit der Formel $A=\pi\cdot d\cdot h$ berechnen. Einsetzen der gegebenen Größen liefert den Flächeninhalt der Mantelfläche des Turms:

$\begin{array}[t]{rll} A&=& \pi\cdot 3,70\,\text{m}\cdot 72,20\,\text{m} \\[5pt] &\approx& 840\,\text{m}^2 \end{array}$

Für einen Quadratmeter werden 0,5 Liter Farbe benötigt:

$840\,\text{m}^2\cdot 0,5\,\dfrac{\ell}{\text{m}^2}=420\,\ell$

Für den Schutzanstrich werden 420 Liter Farbe benötigt.

3.2

Streckenlänge berechnen

Skizze zum Sachverhalt:

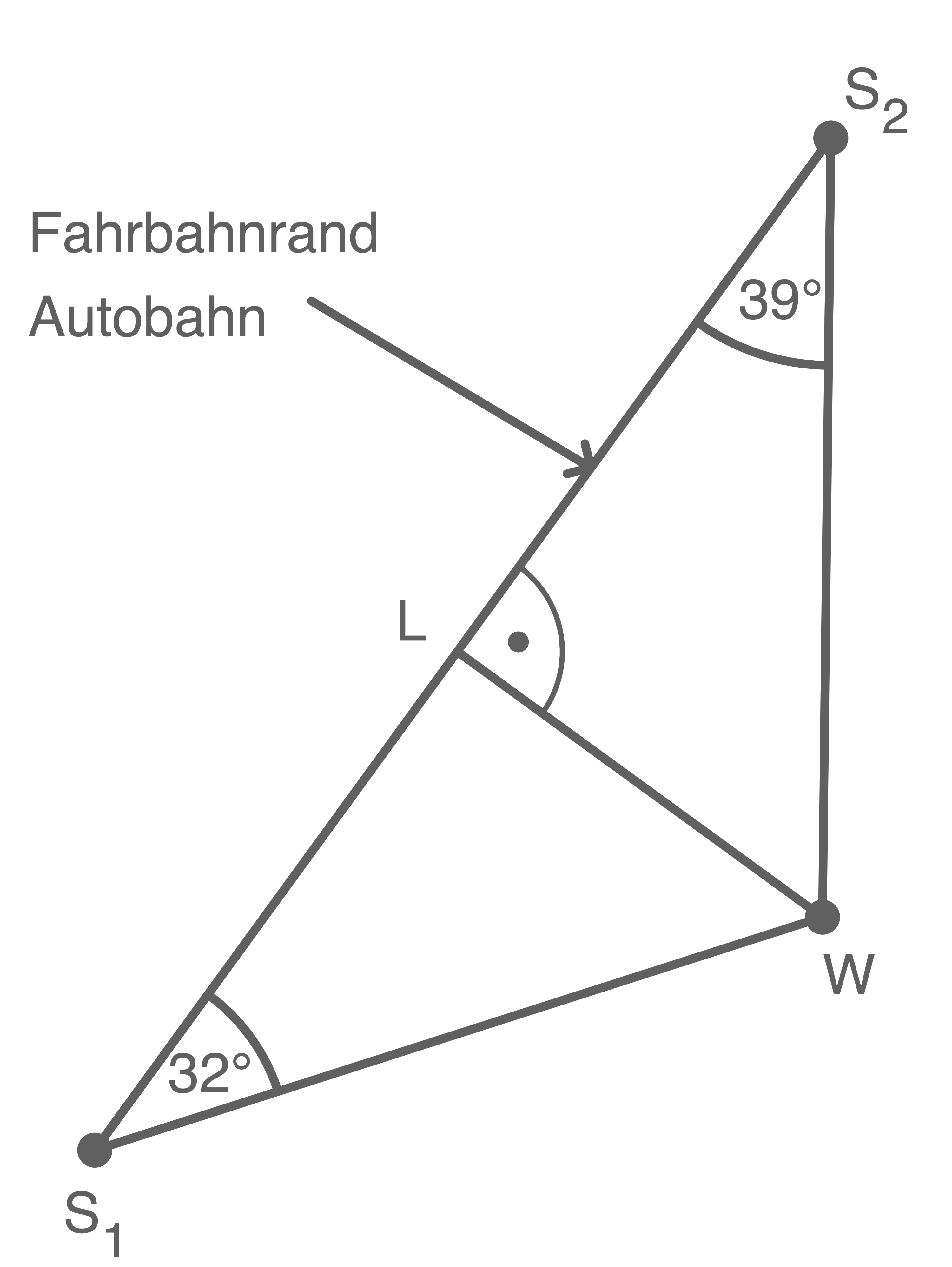Nach dem Innenwinkelsatz für Dreiecke muss der Winkel $\sphericalangle S_2WS_1$ eine Größe von $180^°-32^°-39^°=109^°$ haben. Mit dem Sinussatz folgt:

Rechenweg anzeigen

$\overline{S_1W} \approx 233 \,\text{m}$

Dir Strecke $\overline{S_1W}$ ist 233 Meter lang.

Einhaltung des Mindestabstands überprüfen

Es gilt zu überprüfen, ob die Strecke $\overline{WL},$ die die kürzeste Vebindung zwischen dem Punkt $W$ und der Strecke $S_1S_2$ darstellt, größer als der Mindestabstand ist. Es gilt:

$\begin{array}[t]{rll} \sin \sphericalangle WS_1L&=& \dfrac{\overline{LW}}{\overline{S_1W}} \\[5pt] \sin 32^°&=& \dfrac{\overline{LW}}{233\,\text{m}} \quad \scriptsize \mid\;\cdot 233\,\text{m} \\[5pt] \sin 32^°\cdot 233\,\text{m}&=& \overline{LW} \\[5pt] 123 \,\text{m}&\approx& \overline{LW} \end{array}$

Der Abstand ist größer als 100 Meter. Der gesetzliche Mindestabstand wird daher eingehalten.

3.3.1

Gesucht ist die Lösung der Gleichung $P(t)=1\,000.$ Zur Lösung dieser Gleichung kann mit dem CAS der Schnittpunkt der Graphen von $P$ und der Funktion $y=1\,000$ berechnet werden.

menu $\rightarrow$ 6: Graph analysieren $\rightarrow$ 4: Schnittpunkt

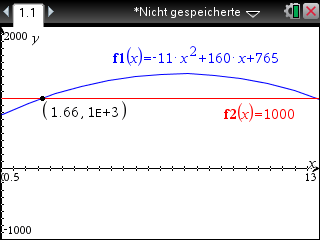Graphische Darstellung von zwei Funktionen f1 und f2 auf einem Koordinatensystem.

Zur Zeit t $\approx$ $1,66$ gab die Windkraftanlage eine elektrische Leistung von genau $1000$ Kilowatt ab. Die andere Lösung der Gleichung liegt nicht im angegebenen Definitionsbereich.

3.3.2

Die größte elektrische Leistung, die von der Windkraftanlage abgegeben wurde, ergibt sich durch Bestimmung des Hochpunkts des Graphen der Funktion $P.$

menu $\rightarrow$ 6: Graph analysieren $\rightarrow$ 3: Maximum

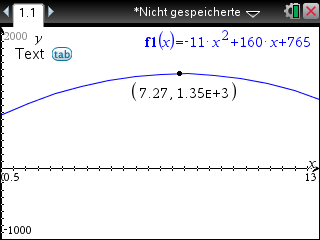Grafik einer Parabel mit der Funktion f1(x) und einem markierten Punkt.

Die größte elektrische Leistung, die von der Windkraftanlage abgegeben wurde, beträgt ungefähr $1\,346$ Kilowatt.

3.3.3

Irgendwann in den ersten $10$ Stunden steigt die von der Windkraftanlage abgegebene elektrische Leistung ab dem Zeitpunkt $t_1$ während $2$ Stunden um genau $100$ Kilowatt. Die Differenz zwischen den beiden Funktionswerten $P(t_1)$ und $P(t_1+2)$ soll also $100$ sein. Um den Wert $t_1$ zu bestimmen, muss die Gleichung aufgestellt und nach $t_1$ aufgelöst werden.

Gleichung anzeigen

$100 = P(t_1+2)-P(t_1)$

Der CAS liefert die Lösung $t_1=4.$

Ab der Zeit $t_1=4$ steigt die abgegebene elektrische Leistung in zwei Stunden (bis zum Zeitpunkt $t_2=6$ ) um genau $100$ Kilowatt.

3.4

Eine Windkraftanlage muss während 18,4 % der Gesamtbetriebszeit abgeschaltet werden.

Zu 47 % dieser Zeit davon wird die Anlage wegen zu schwachen Windes abgeschaltet.

Der Anteil dieses Abschaltgrundes während der Gesamtbetriebszeit lässt sich wie folgt berechnen:

$0,184\cdot 0,47=0,08648=8,648 \,\%$

Ungefähr 8,6 % der Gesamtbetriebszeit muss die Anlage wegen zu schwachen Windes abgeschaltet werden.

1.1

Wertebereich angeben

Die Funktion $f(x)=3^x$ ist eine Exponentialfunktion mit positiver Basis $a=3.$ Nach Definition nimmt diese nur Werte größer als $0$ an.

Wertebereich: $y \in R, y\gt 0$

Schnittpunkt mit y-Achse angeben

$f(0)=3^0=1$

Schnittpunkt mit der $y$ -Achse: $P(0\mid 1)$

1.2

Gesucht ist die Lösung der Gleichung $\dfrac {1}{81}=3^{x_A+1}$ . Diese kann man mit dem CAS berechnet werden, indem der Schnittpunkt von $g$ mit der Geraden $a=\dfrac{1}{81}$ bestimmt wird.

Analyse $\rightarrow$ Grafische Lösung $\rightarrow$ Schnittpunkt

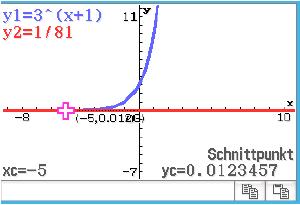Graph der Funktionen y1 und y2 mit Schnittpunkt bei xc=-5 und yc=0.0123457.

Die Koordinate $x_a$ hat den Wert $-5.$

1.3

$g(0)=3^{0+1}=3$

Damit folgt $Q(0\mid 3).$ Die Koordinaten des Punkts $P(0\mid 1)$ sind aus Aufgabe 1.1 bekannt.

Skizze des Sachverhalts

Der Flächeninhalt eines Dreiecks lässt sich mit der Formel $A=\dfrac{1}{2}\cdot g\cdot h$ berechnen. Hier gilt:

$g=\overline{PQ}=2$
$h=\overline{OB}=2$

$A=\dfrac{1}{2}\cdot 2\cdot 2=2$

Der Flächeninhalt des Dreiecks $PBQ$ beträgt 2.

2.1

Rechenweg anzeigen

$E=14,144\,\text{h}$

Das arithmetische Mittel der Siegerzeiten beträgt $14,144 \mathrm{~h}.$

2.2

$n=3\cdot 2\cdot 1=6$

Es gibt 6 mögliche Startreihenfolgen.

2.3

Auf einer Karte im Maßstab $1:10\,000$ ist der Abschnitt des konstanten Anstiegs $1,9\,\text{cm}$ lang. Das heißt, dass dieser Abschnitt in der Realität

$1,9\,\text{cm}\cdot 10\,000=19\,000\text{cm}=190\,\text{m}$

lang ist.

Der Sachverhalt lässt sich wie folgt darstellen:

Mit dem Satz des Pythagoras lässt sich nun die Läange $\ell$ der Laufstrecke berechnen:

$\begin{array}[t]{rll} \ell^2&=& (190\,\text{m})^2+(73,4\,\text{m})^2 \\[5pt] \ell^2&=& 41\,487,56 \,\text{m}^2 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt] \ell&\approx& 204\,\text{m} \end{array}$

Die Länge der Laufstrecke beträgt ungefähr 204 Meter.

3.1

Die Mantelfläche eines Zylinders lässt sich mit der Formel $A=\pi\cdot d\cdot h$ berechnen. Einsetzen der gegebenen Größen liefert den Flächeninhalt der Mantelfläche des Turms:

$\begin{array}[t]{rll} A&=& \pi\cdot 3,70\,\text{m}\cdot 72,20\,\text{m} \\[5pt] &\approx& 840\,\text{m}^2 \end{array}$

Für einen Quadratmeter werden 0,5 Liter Farbe benötigt:

$840\,\text{m}^2\cdot 0,5\,\dfrac{\ell}{\text{m}^2}=420\,\ell$

Für den Schutzanstrich werden 420 Liter Farbe benötigt.

3.2

Streckenlänge berechnen

Skizze zum Sachverhalt:

Nach dem Innenwinkelsatz für Dreiecke muss der Winkel $\sphericalangle S_2WS_1$ eine Größe von $180^°-32^°-39^°=109^°$ haben. Mit dem Sinussatz folgt:

Rechenweg anzeigen

$\overline{S_1W} \approx 233 \,\text{m}$

Dir Strecke $\overline{S_1W}$ ist 233 Meter lang.

Einhaltung des Mindestabstands überprüfen

Es gilt zu überprüfen, ob die Strecke $\overline{WL},$ die die kürzeste Vebindung zwischen dem Punkt $W$ und der Strecke $S_1S_2$ darstellt, größer als der Mindestabstand ist. Es gilt:

Der Abstand ist größer als 100 Meter. Der gesetzliche Mindestabstand wird daher eingehalten.

3.3.1

Gesucht ist die Lösung der Gleichung $P(t)=1\,000.$ Zur Lösung dieser Gleichung kann mit dem CAS der Schnittpunkt der Graphen von $P$ und der Funktion $y=1\,000$ berechnet werden.

Analyse $\rightarrow$ Grafische Lösung $\rightarrow$ Schnittpunkt

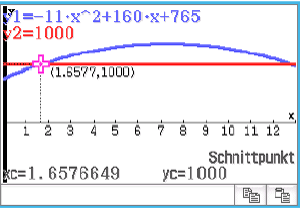Graph einer Funktion mit Schnittpunkten und Achsenbeschriftungen.

Zur Zeit t $\approx$ $1,66$ gab die Windkraftanlage eine elektrische Leistung von genau $1000$ Kilowatt ab. Die andere Lösung der Gleichung liegt nicht im angegebenen Definitionsbereich.

3.3.2

Die größte elektrische Leistung, die von der Windkraftanlage abgegeben wurde, ergibt sich durch Bestimmung des Hochpunkts des Graphen der Funktion $P.$

Analyse $\rightarrow$ Grafische Lösung $\rightarrow$ Maximum

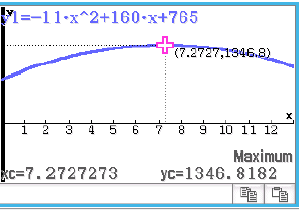Grafik einer Parabel mit einer maximalen Koordinate bei (7.27, 1346.82).

Die größte elektrische Leistung, die von der Windkraftanlage abgegeben wurde, beträgt ungefähr $1\,346$ Kilowatt.

3.3.3

Gleichung anzeigen

$100 = P(t_1+2)-P(t_1)$

Der CAS liefert die Lösung $t_1=4.$

Ab der Zeit $t_1=4$ steigt die abgegebene elektrische Leistung in zwei Stunden (bis zum Zeitpunkt $t_2=6$ ) um genau $100$ Kilowatt.

3.4

Eine Windkraftanlage muss während 18,4 % der Gesamtbetriebszeit abgeschaltet werden.

Zu 47 % dieser Zeit davon wird die Anlage wegen zu schwachen Windes abgeschaltet.

Der Anteil dieses Abschaltgrundes während der Gesamtbetriebszeit lässt sich wie folgt berechnen:

$0,184\cdot 0,47=0,08648=8,648 \,\%$

Ungefähr 8,6 % der Gesamtbetriebszeit muss die Anlage wegen zu schwachen Windes abgeschaltet werden.