Teil B
1
Gegeben sind die Funktionen  und
und  mit
mit

 und
und 
 Die Punkte
Die Punkte  und
und  sind die beiden gemeinsamen Punkte der Graphen der Funktionen
sind die beiden gemeinsamen Punkte der Graphen der Funktionen  und
und 
1.1
Gib den größtmöglichen Definitionsbereich der Funktion  an.
an.
(1 BE)
1.2
Zeige, dass der Punkt  die Koordinaten
die Koordinaten  besitzt.
besitzt.
(2 BE)
1.3
Berechne den Abstand der Punkte  und
und 
(2 BE)
1.4
Der Punkt  ist der Fußpunkt des Lotes vom Punkt
ist der Fußpunkt des Lotes vom Punkt  auf die
auf die  -Achse.
-Achse.
Der Punkt ist der Fußpunkt des Lotes vom Punkt
ist der Fußpunkt des Lotes vom Punkt  auf die
auf die  -Achse.
Ermittle den Flächeninhalt des Trapezes
-Achse.
Ermittle den Flächeninhalt des Trapezes 
Der Punkt
(2 BE)
1.5
Der Graph einer linearen Funktion  verläuft parallel zum Graphen der Funktion
verläuft parallel zum Graphen der Funktion 
Der Punkt liegt auf dem Graphen von
liegt auf dem Graphen von  Bestimme eine Gleichung dieser Funktion
Bestimme eine Gleichung dieser Funktion 
Der Punkt
(2 BE)
2
Ein Pfeiler ist  hoch und besitzt die Form eines geraden Prismas. Die Grundfläche dieses Prismas ist das unregelmäßige Dreieck
hoch und besitzt die Form eines geraden Prismas. Die Grundfläche dieses Prismas ist das unregelmäßige Dreieck 
Für die Grundfläche gilt:
 und
und 
Für die Grundfläche gilt:
2.1
Zeige rechnerisch, dass die Seite  der Grundfläche die Länge
der Grundfläche die Länge  besitzt.
besitzt.
(2 BE)
2.2
Der Pfeiler besteht aus Stahl. Ein Kubikmeter dieses Stahls besitzt eine Masse von  Tonnen.
Tonnen.
Bestimme die Masse des Pfeilers.
Bestimme die Masse des Pfeilers.
(3 BE)
3
Ein rechteckiges Handballspielfeld wird von  und
und  langen Spielfeldlinienbegrenzt. Die
langen Spielfeldlinienbegrenzt. Die  langen Torlinien liegen mittig auf den kürzeren Spielfeldlinien (siehe Abbildung).
langen Torlinien liegen mittig auf den kürzeren Spielfeldlinien (siehe Abbildung).
Die Breite aller Spielfeldlinien wird vernachlässigt.
Die Breite aller Spielfeldlinien wird vernachlässigt.

Abbildung (nicht maßstäblich)
3.1
Jeder der beiden Torräume wird von einer Torraumlinie begrenzt, die wie folgt festgelegt ist:
Um die Endpunkte der Torlinie wird jeweils ein Kreisbogen (Viertelkreis) mit einem Radius von gezogen bis er auf eine Strecke trifft, die in einem Abstand von
gezogen bis er auf eine Strecke trifft, die in einem Abstand von  parallel zur Torlinie verläuft.
Berechne den prozentualen Anteil der Fläche der beiden Torräume an der Gesamtfläche des Handballspielfeldes.
parallel zur Torlinie verläuft.
Berechne den prozentualen Anteil der Fläche der beiden Torräume an der Gesamtfläche des Handballspielfeldes.
Um die Endpunkte der Torlinie wird jeweils ein Kreisbogen (Viertelkreis) mit einem Radius von
(4 BE)
3.2
Ein Torwart wirft einen Ball. Die Ausdehnung des Balls wird vernachlässigt. Um die Flugbahn dieses Balls zu beschreiben, wird ein Koordinatensystem ( Längeneinheit entspricht
Längeneinheit entspricht  Meter) festgelegt.
Meter) festgelegt.
Der Koordinatenursprung befindet sich im Mittelpunkt der in der Abbildung dargestellten linken Torlinie. Die Mittelpunkte beider Torlinien liegen auf der -Achse. Die
-Achse. Die  -Achse verläuft senkrecht zum Spielfeld.
-Achse verläuft senkrecht zum Spielfeld.
Die Flugbahn des Balls wird durch einen Teil des Graphen der Funktion mit
mit

 beschrieben.
beschrieben.
Der -Wert gibt die jeweilige Höhe des Balls über dem Spielfeld an.
-Wert gibt die jeweilige Höhe des Balls über dem Spielfeld an.
Der Torwart wirft den Ball im Punkt ab.
ab.
Der Koordinatenursprung befindet sich im Mittelpunkt der in der Abbildung dargestellten linken Torlinie. Die Mittelpunkte beider Torlinien liegen auf der
Die Flugbahn des Balls wird durch einen Teil des Graphen der Funktion
Der
Der Torwart wirft den Ball im Punkt
3.2.1
Gib an, in welcher Höhe über dem Spielfeld der Torwart den Ball abwirft.
Bestimme die größte Höhe des Balls über dem Spielfeld bei dieser Flugbahn.
Bestimme die größte Höhe des Balls über dem Spielfeld bei dieser Flugbahn.
(3 BE)
3.2.2
Untersuche, ob der Ball bei dieser Flugbahn auf dem Spielfeld auftreffen könnte.
(2 BE)
3.2.3
Ein Spieler fängt den Ball im Punkt 
Jeder Punkt der gestrichelten Freiwurflinie (siehe Abbildung) hat von der Torlinie einen Abstand von Zeige, dass der Spieler den Ball senkrecht über einer Freiwurflinie fängt.
Zeige, dass der Spieler den Ball senkrecht über einer Freiwurflinie fängt.
Jeder Punkt der gestrichelten Freiwurflinie (siehe Abbildung) hat von der Torlinie einen Abstand von
(3 BE)
3.3
Die Wahrscheinlichkeit dafür, dass Torwart Marian einen Siebenmeterwurf hält, beträgt 
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
Berechne die Wahrscheinlichkeiten folgender Ereignisse:
Ereignis 
Marian hält einen von drei Siebenmeterwürfen.
Ereignis 
Marian hält keinen von drei Siebenmeterwürfen.
(4 BE)
1.1
Bei  handelt es sich um eine gebrochenrationale Funktion. Der Nenner des Bruchs darf nicht null werden. Mögliche Definitionslücken sind also die Nullstellen des Nenners.
handelt es sich um eine gebrochenrationale Funktion. Der Nenner des Bruchs darf nicht null werden. Mögliche Definitionslücken sind also die Nullstellen des Nenners.
![\(\begin{array}[t]{rll}
x^2&=& 0\quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
x&=&0
\end{array}\)](https://mathjax.schullv.de/bfc5fea9499d85009c4a9fbfc6434674a74a2e42509e53fe1f6dc34a7561de97?color=5a5a5a) Der größtmögliche Definitionsbereich von
Der größtmögliche Definitionsbereich von  ist
ist 
1.2
Für  gilt:
gilt:
![\(\begin{array}[t]{rll}
f(-1)&=& \dfrac{2}{(-1)^2} \\[5pt]
&=& \dfrac{2}{1}\\[5pt]
&=& 2
\end{array}\)](https://mathjax.schullv.de/bd6c4489afc0d40b7b5cfbfc1934378dca876fbd638fd306818d64d23747310f?color=5a5a5a) Für
Für  gilt:
gilt:
![\(\begin{array}[t]{rll}
g(-1)&=& -\dfrac{1}{2}\cdot (-1) + \dfrac{3}{2}\\[5pt]
&=& \dfrac{1}{2}+\dfrac{3}{2}\\[5pt]
&=& 2
\end{array}\)](https://mathjax.schullv.de/c7a9a702f0d7936db390f45b90d7ddac89c8f8d57f96a36e57a3f9acb7e7df84?color=5a5a5a) Der Punkt
Der Punkt  mit den Koordinaten
mit den Koordinaten  liegt auf den Graphen der beiden Funktionen
liegt auf den Graphen der beiden Funktionen  und
und  und ist daher der zweite gemeinsame Punkt der beiden Graphen.
und ist daher der zweite gemeinsame Punkt der beiden Graphen.
1.3
Mit der Formel für den Abstand zweier Punkte ergibt sich:
![\(\begin{array}[t]{rll}
d\left(S_1,S_2\right)&=&\sqrt{\left(x_{S_2}-x_{S_1}\right)^2+\left(y_{S_2}-y_{S_1}\right)^2} \\[5pt]
&=& \sqrt{(2-(-1))^2+\left(\dfrac{1}{2}-2\right)^2}\\[5pt]
&=& \dfrac{3\sqrt{5}}{2} \\[5pt]
&\approx& 3,35
\end{array}\)](https://mathjax.schullv.de/54e18640d59a1e192a99108bcdbd2c642e06a93ce553f254c0b323a2a42beedf?color=5a5a5a) Die beiden Punkte
Die beiden Punkte  und
und  haben einen Abstand von
haben einen Abstand von  Längeneinheiten.
Längeneinheiten.
1.4
Die beiden parallelen Seiten des Trapezes sind  und
und  deren Längen sich über die
deren Längen sich über die  -Koordinaten der Punkte
-Koordinaten der Punkte  bzw.
bzw.  ergeben.
ergeben.
Aufgrund der beiden rechten Winkel, die in der Skizze eingezeichnet sind, ist die Höhe des Trapezes gerade die Länge der Strecke die sich wiederum über die Summe der Beträge der
die sich wiederum über die Summe der Beträge der  -Koordinaten von
-Koordinaten von  und
und  ergibt.
ergibt.
Aufgrund der beiden rechten Winkel, die in der Skizze eingezeichnet sind, ist die Höhe des Trapezes gerade die Länge der Strecke
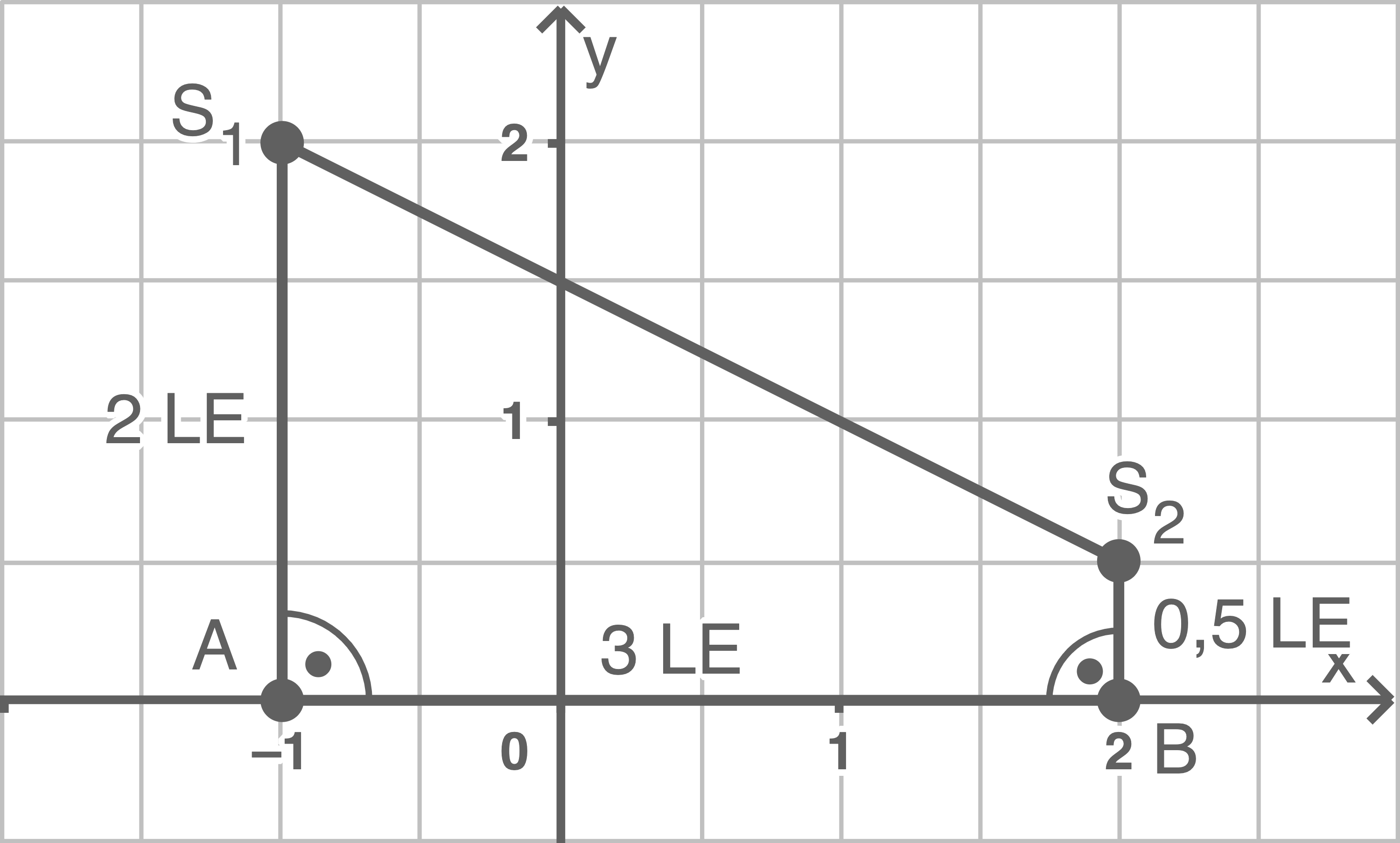
Skizze
1.5
Eine mögliche Gleichung der Funktion  hat die Form
hat die Form  Da der Graph von
Da der Graph von  parallel zu dem von
parallel zu dem von  verlaufen soll, muss die Steigung identisch sein, also ist
verlaufen soll, muss die Steigung identisch sein, also ist 
Der Punkt soll auf dem Graphen von
soll auf dem Graphen von  liegen. Mit einer Punktprobe ergibt sich:
liegen. Mit einer Punktprobe ergibt sich:
![\(\begin{array}[t]{rll}
h(x)&=& -\dfrac{1}{2}x+b \quad \scriptsize \mid\;h(2) = 1 \\[5pt]
1&=& -\dfrac{1}{2}\cdot 2 +b \\[5pt]
1&=& -1+b \quad \scriptsize \mid\;+1 \\[5pt]
2&=& b
\end{array}\)](https://mathjax.schullv.de/4b5b31412aae039aa2102ab785a60c3824411337f55710543906ce8b174f8972?color=5a5a5a) Eine Gleichung der Funktion
Eine Gleichung der Funktion  ist
ist 
Der Punkt
2.1
Der Winkel  kann über die Winkelsumme eines Dreiecks berechnet werden:
kann über die Winkelsumme eines Dreiecks berechnet werden:
![\(\begin{array}[t]{rll}
180^{\circ}&=& 48^{\circ}+30^{\circ} +\sphericalangle ACB \\[5pt]
180^{\circ}&=& 78^{\circ}+\sphericalangle ACB \quad \scriptsize \mid\;-78^{\circ} \\[5pt]
102^{\circ}&=& \sphericalangle ACB
\end{array}\)](https://mathjax.schullv.de/b7c3d07bad206adb60850b8cce48d8782a400c131d11f00ac6c3109289563c1a?color=5a5a5a)
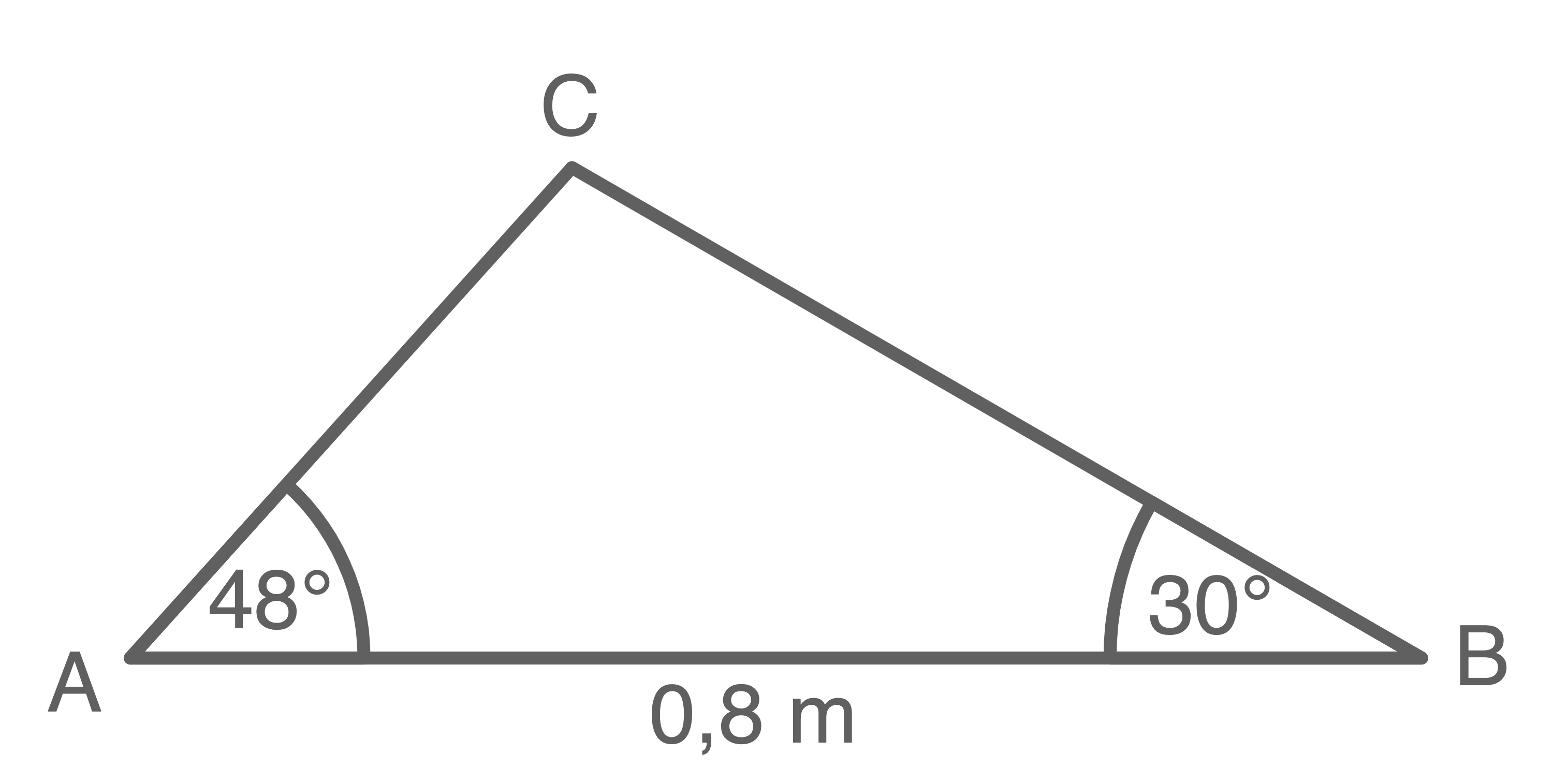
Skizze
2.2
Der Flächeninhalt der Grundfläche ergibt sich mit der Formel für den Flächeninhalt eines Dreiecks wie folgt:
![\(\begin{array}[t]{rll}
A_{G}&=& \dfrac{1}{2}\cdot \overline{AC} \cdot \overline{AB}\cdot \sin \alpha \\[5pt]
&=& \dfrac{1}{2}\cdot 0,41\,\text{m} \cdot 0,8\,\text{m}\cdot \sin 48^{\circ} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/eefd7241cdd5cbe2c803ffcd012324df22e9756601e1799de4a6d4e50eb29986?color=5a5a5a) Das Volumen des prismenförmigen Pfeilers ergibt sich dadurch mit der entsprechenden Formel zu:
Das Volumen des prismenförmigen Pfeilers ergibt sich dadurch mit der entsprechenden Formel zu:
![\(\begin{array}[t]{rll}
V&=& A_G \cdot h\quad \scriptsize \mid\;h =3,60\,\text{m} \\[5pt]
&=&\dfrac{1}{2}\cdot 0,41\,\text{m} \cdot 0,8\,\text{m}\cdot \sin 48^{\circ} \cdot 3,60\,\text{m}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/13280e4780cf0818a3a8ba39b613ccb67394cd7a68127fff0cf980cc36ecf9db?color=5a5a5a) Die Masse ergibt sich daher zu:
Der Pfeiler besitzt eine Masse von ca.
Die Masse ergibt sich daher zu:
Der Pfeiler besitzt eine Masse von ca.  Tonnen.
Tonnen.
3.1
1. Schritt: Inhalt der Gesamtfläche berechnen
Der Flächeninhalt des rechteckigen Spielfeldes ergibt sich mit den beiden Seitenlängen  und
und  wie folgt:
wie folgt:
![\(\begin{array}[t]{rll}
A_{\text{Gesamt}}&=&40,00\,\text{m}\cdot 20,00\,\text{m} \\[5pt]
&=& 800,00\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/0862fbd9cc1e5069055ee28bec23fba5c02671bf2a042446c2f6c3b068784c17?color=5a5a5a) 2. Schritt: Flächeninhalt der Torräume berechnen
2. Schritt: Flächeninhalt der Torräume berechnen
 Für den Gesamtflächeninhalt der beiden Torräume gilt mit der Formel für den Flächeninhalt eines Kreises:
Für den Gesamtflächeninhalt der beiden Torräume gilt mit der Formel für den Flächeninhalt eines Kreises:
![\(\begin{array}[t]{rll}
A_{\text{Torräume}}&=& \pi \cdot \left( 6\,\text{m}\right)^2+ 2\cdot 6\,\text{m}\cdot 3\,\text{m} \\[5pt]
&\approx& 149,10\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/acd694e508dce4fa60bc9d481eb66f64a18b8d8b76b692f4ce5e898efc22d148?color=5a5a5a) 3. Schritt: Prozentualen Anteil berechnen
3. Schritt: Prozentualen Anteil berechnen
![\(\begin{array}[t]{rll}
\dfrac{A_{\text{Torräume}}}{A_{\text{Gesamt}}}&=& \dfrac{149,10\,\text{m}^2}{800,00\,\text{m}^2}\\[5pt]
&\approx&0,186\\[5pt]
&=& 18,6\,\%
\end{array}\)](https://mathjax.schullv.de/8ffa9343b74cbbd71ec6647718331d30476aa54d9d3e07a52f0ee4800f1b1d58?color=5a5a5a) Die Flächen der beiden Torräume bilden gemeinsam ca.
Die Flächen der beiden Torräume bilden gemeinsam ca.  der gesamten Spielfeldfläche.
der gesamten Spielfeldfläche.
Beide Torräume setzen sich gemeinsam zusammen aus
- vier Viertelkreisen mit dem Radius
die gemeinsam den Flächeninhalt eines Kreises mit dem Radius
haben,
- und zwei Rechtecken mit den Seitenlängen
und

Skizze
3.2.1
Höhe des Abwurfs berechnen
Der Torwart wirft den Ball im Punkt  ab. Der
ab. Der  -Wert der Funktion
-Wert der Funktion  gibt die Höhe des Balls über dem Spielfeld an.
Der Torwart wirft den Ball in einer Höhe von
gibt die Höhe des Balls über dem Spielfeld an.
Der Torwart wirft den Ball in einer Höhe von  ab.
Größte Höhe des Balls bestimmen
Bei dem Graphen der Funktion
ab.
Größte Höhe des Balls bestimmen
Bei dem Graphen der Funktion  handelt es sich um eine nach unten geöffnete Parabel. Der Punkt, an dem sich der Ball am höchsten befindet, wird daher durch den Scheitelpunkt der Parabel beschrieben.
handelt es sich um eine nach unten geöffnete Parabel. Der Punkt, an dem sich der Ball am höchsten befindet, wird daher durch den Scheitelpunkt der Parabel beschrieben.
 TI nspire CAS
Der CAS liefert die Koordinaten des Scheitelpunkts
TI nspire CAS
Der CAS liefert die Koordinaten des Scheitelpunkts  Die größte Höhe des Balls über dem Spielfeld beträgt also
Die größte Höhe des Balls über dem Spielfeld beträgt also 
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
3.2.2
Der Auftreffpunkt des Balls auf dem Boden wird durch den Punkt beschrieben, in dem der Graph von  für
für  die
die  -Achse schneidet. Gesucht ist also die passende Nullstelle der Funktion
-Achse schneidet. Gesucht ist also die passende Nullstelle der Funktion  Der solve-efehl des CAS liefert für
Der solve-efehl des CAS liefert für  die Lösungen
die Lösungen  und
und  Aufgrund des Definitionsbereichs der Funktion ist nur
Aufgrund des Definitionsbereichs der Funktion ist nur  eine zulässige Lösung.
Der Ball würde also nach
eine zulässige Lösung.
Der Ball würde also nach  aufkommen. Addiert man die
aufkommen. Addiert man die  die der Torwart vor der Linie steht, so würde der Ball trotzdem noch im
die der Torwart vor der Linie steht, so würde der Ball trotzdem noch im  langen Spielfeld aufkommen.
langen Spielfeld aufkommen.
3.2.3
Der Mittelpunkt der linken Torlinie wird durch den Punkt  beschrieben, der Mittelpunkt der rechten Torlinie durch
beschrieben, der Mittelpunkt der rechten Torlinie durch  Die beiden Freiwurflinien sind in jedem Punkt genau
Die beiden Freiwurflinien sind in jedem Punkt genau  Meter von der jeweiligen Torlinie entfernt. Auf jeder Freiwurflinie gibt es genau einen Punkt, der senkrecht unterhalb der Flugbahn des Balls liegt. Diese beiden Punkte haben im Koordinatensystem die Koordinaten
Meter von der jeweiligen Torlinie entfernt. Auf jeder Freiwurflinie gibt es genau einen Punkt, der senkrecht unterhalb der Flugbahn des Balls liegt. Diese beiden Punkte haben im Koordinatensystem die Koordinaten  und
und  Der Ball wird in einer Höhe von
Der Ball wird in einer Höhe von  gefangen. Gesucht ist also der
gefangen. Gesucht ist also der  -Wert zum
-Wert zum  Mit dem solve-Befehl des CAS folgt
Mit dem solve-Befehl des CAS folgt  Die zweite Lösung
Die zweite Lösung  liegt außerhalb des Spielfeldes.
Der Ball wird also in dem Punkt gefangen, der im Koordinatensystem durch
liegt außerhalb des Spielfeldes.
Der Ball wird also in dem Punkt gefangen, der im Koordinatensystem durch  beschrieben wird. Dieser Punkt liegt senkrecht über dem Punkt
beschrieben wird. Dieser Punkt liegt senkrecht über dem Punkt  der den Punkt auf der rechten Freiwurflinie senkrecht unterhalb der Flugbahn des Balls beschreibt.
Der Ball wird also senkrecht über der Freiwurflinie gefangen.
der den Punkt auf der rechten Freiwurflinie senkrecht unterhalb der Flugbahn des Balls beschreibt.
Der Ball wird also senkrecht über der Freiwurflinie gefangen.
3.3
Die Wahrscheinlichkeit, dafür dass Marian einen Siebenmeterwurf hält, beträgt  dafür dass er einen Siebenmeterwurf nicht hält also
dafür dass er einen Siebenmeterwurf nicht hält also  Mit den Pfadregeln ergibt sich:
Mit den Pfadregeln ergibt sich:
![\(\begin{array}[t]{rll}
P(A)&=& 3\cdot 0,22\cdot 0,78\cdot 0,78 \\[5pt]
&\approx& 0,402\\[5pt]
&=& 40,2\,\%\\[10pt]
P(B)&=& 0,78\cdot 0,78\cdot 0,78 \\[5pt]
&\approx& 0,475\\[5pt]
&=& 47,5\,\%
\end{array}\)](https://mathjax.schullv.de/020e5d06e35a248f3e8ecd4f043edd5bd9f7c00c855cb4a71066f6faf7b07775?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  hält Marian genau einen von drei Siebenmeterwürfen. Mit einer Wahrscheinlichkeit von ca.
hält Marian genau einen von drei Siebenmeterwürfen. Mit einer Wahrscheinlichkeit von ca.  hält er keinen von drei Siebenmeterwürfen.
hält er keinen von drei Siebenmeterwürfen.
1.1
Bei  handelt es sich um eine gebrochenrationale Funktion. Der Nenner des Bruchs darf nicht null werden. Mögliche Definitionslücken sind also die Nullstellen des Nenners.
handelt es sich um eine gebrochenrationale Funktion. Der Nenner des Bruchs darf nicht null werden. Mögliche Definitionslücken sind also die Nullstellen des Nenners.
![\(\begin{array}[t]{rll}
x^2&=& 0\quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
x&=&0
\end{array}\)](https://mathjax.schullv.de/bfc5fea9499d85009c4a9fbfc6434674a74a2e42509e53fe1f6dc34a7561de97?color=5a5a5a) Der größtmögliche Definitionsbereich von
Der größtmögliche Definitionsbereich von  ist
ist 
1.2
Für  gilt:
gilt:
![\(\begin{array}[t]{rll}
f(-1)&=& \dfrac{2}{(-1)^2} \\[5pt]
&=& \dfrac{2}{1}\\[5pt]
&=& 2
\end{array}\)](https://mathjax.schullv.de/bd6c4489afc0d40b7b5cfbfc1934378dca876fbd638fd306818d64d23747310f?color=5a5a5a) Für
Für  gilt:
gilt:
![\(\begin{array}[t]{rll}
g(-1)&=& -\dfrac{1}{2}\cdot (-1) + \dfrac{3}{2}\\[5pt]
&=& \dfrac{1}{2}+\dfrac{3}{2}\\[5pt]
&=& 2
\end{array}\)](https://mathjax.schullv.de/c7a9a702f0d7936db390f45b90d7ddac89c8f8d57f96a36e57a3f9acb7e7df84?color=5a5a5a) Der Punkt
Der Punkt  mit den Koordinaten
mit den Koordinaten  liegt auf den Graphen der beiden Funktionen
liegt auf den Graphen der beiden Funktionen  und
und  und ist daher der zweite gemeinsame Punkt der beiden Graphen.
und ist daher der zweite gemeinsame Punkt der beiden Graphen.
1.3
Mit der Formel für den Abstand zweier Punkte ergibt sich:
![\(\begin{array}[t]{rll}
d\left(S_1,S_2\right)&=&\sqrt{\left(x_{S_2}-x_{S_1}\right)^2+\left(y_{S_2}-y_{S_1}\right)^2} \\[5pt]
&=& \sqrt{(2-(-1))^2+\left(\dfrac{1}{2}-2\right)^2}\\[5pt]
&=& \dfrac{3\sqrt{5}}{2} \\[5pt]
&\approx& 3,35
\end{array}\)](https://mathjax.schullv.de/54e18640d59a1e192a99108bcdbd2c642e06a93ce553f254c0b323a2a42beedf?color=5a5a5a) Die beiden Punkte
Die beiden Punkte  und
und  haben einen Abstand von
haben einen Abstand von  Längeneinheiten.
Längeneinheiten.
1.4
Die beiden parallelen Seiten des Trapezes sind  und
und  deren Längen sich über die
deren Längen sich über die  -Koordinaten der Punkte
-Koordinaten der Punkte  bzw.
bzw.  ergeben.
ergeben.
Aufgrund der beiden rechten Winkel, die in der Skizze eingezeichnet sind, ist die Höhe des Trapezes gerade die Länge der Strecke die sich wiederum über die Summe der Beträge der
die sich wiederum über die Summe der Beträge der  -Koordinaten von
-Koordinaten von  und
und  ergibt.
ergibt.
Aufgrund der beiden rechten Winkel, die in der Skizze eingezeichnet sind, ist die Höhe des Trapezes gerade die Länge der Strecke

Skizze
1.5
Eine mögliche Gleichung der Funktion  hat die Form
hat die Form  Da der Graph von
Da der Graph von  parallel zu dem von
parallel zu dem von  verlaufen soll, muss die Steigung identisch sein, also ist
verlaufen soll, muss die Steigung identisch sein, also ist 
Der Punkt soll auf dem Graphen von
soll auf dem Graphen von  liegen. Mit einer Punktprobe ergibt sich:
liegen. Mit einer Punktprobe ergibt sich:
![\(\begin{array}[t]{rll}
h(x)&=& -\dfrac{1}{2}x+b \quad \scriptsize \mid\;h(2) = 1 \\[5pt]
1&=& -\dfrac{1}{2}\cdot 2 +b \\[5pt]
1&=& -1+b \quad \scriptsize \mid\;+1 \\[5pt]
2&=& b
\end{array}\)](https://mathjax.schullv.de/4b5b31412aae039aa2102ab785a60c3824411337f55710543906ce8b174f8972?color=5a5a5a) Eine Gleichung der Funktion
Eine Gleichung der Funktion  ist
ist 
Der Punkt
2.1
Der Winkel  kann über die Winkelsumme eines Dreiecks berechnet werden:
kann über die Winkelsumme eines Dreiecks berechnet werden:
![\(\begin{array}[t]{rll}
180^{\circ}&=& 48^{\circ}+30^{\circ} +\sphericalangle ACB \\[5pt]
180^{\circ}&=& 78^{\circ}+\sphericalangle ACB \quad \scriptsize \mid\;-78^{\circ} \\[5pt]
102^{\circ}&=& \sphericalangle ACB
\end{array}\)](https://mathjax.schullv.de/b7c3d07bad206adb60850b8cce48d8782a400c131d11f00ac6c3109289563c1a?color=5a5a5a)

Skizze
2.2
Der Flächeninhalt der Grundfläche ergibt sich mit der Formel für den Flächeninhalt eines Dreiecks wie folgt:
![\(\begin{array}[t]{rll}
A_{G}&=& \dfrac{1}{2}\cdot \overline{AC} \cdot \overline{AB}\cdot \sin \alpha \\[5pt]
&=& \dfrac{1}{2}\cdot 0,41\,\text{m} \cdot 0,8\,\text{m}\cdot \sin 48^{\circ} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/eefd7241cdd5cbe2c803ffcd012324df22e9756601e1799de4a6d4e50eb29986?color=5a5a5a) Das Volumen des prismenförmigen Pfeilers ergibt sich dadurch mit der entsprechenden Formel zu:
Das Volumen des prismenförmigen Pfeilers ergibt sich dadurch mit der entsprechenden Formel zu:
![\(\begin{array}[t]{rll}
V&=& A_G \cdot h\quad \scriptsize \mid\;h =3,60\,\text{m} \\[5pt]
&=&\dfrac{1}{2}\cdot 0,41\,\text{m} \cdot 0,8\,\text{m}\cdot \sin 48^{\circ} \cdot 3,60\,\text{m}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/13280e4780cf0818a3a8ba39b613ccb67394cd7a68127fff0cf980cc36ecf9db?color=5a5a5a) Die Masse ergibt sich daher zu:
Der Pfeiler besitzt eine Masse von ca.
Die Masse ergibt sich daher zu:
Der Pfeiler besitzt eine Masse von ca.  Tonnen.
Tonnen.
3.1
1. Schritt: Inhalt der Gesamtfläche berechnen
Der Flächeninhalt des rechteckigen Spielfeldes ergibt sich mit den beiden Seitenlängen  und
und  wie folgt:
wie folgt:
![\(\begin{array}[t]{rll}
A_{\text{Gesamt}}&=&40,00\,\text{m}\cdot 20,00\,\text{m} \\[5pt]
&=& 800,00\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/0862fbd9cc1e5069055ee28bec23fba5c02671bf2a042446c2f6c3b068784c17?color=5a5a5a) 2. Schritt: Flächeninhalt der Torräume berechnen
2. Schritt: Flächeninhalt der Torräume berechnen
 Für den Gesamtflächeninhalt der beiden Torräume gilt mit der Formel für den Flächeninhalt eines Kreises:
Für den Gesamtflächeninhalt der beiden Torräume gilt mit der Formel für den Flächeninhalt eines Kreises:
![\(\begin{array}[t]{rll}
A_{\text{Torräume}}&=& \pi \cdot \left( 6\,\text{m}\right)^2+ 2\cdot 6\,\text{m}\cdot 3\,\text{m} \\[5pt]
&\approx& 149,10\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/acd694e508dce4fa60bc9d481eb66f64a18b8d8b76b692f4ce5e898efc22d148?color=5a5a5a) 3. Schritt: Prozentualen Anteil berechnen
3. Schritt: Prozentualen Anteil berechnen
![\(\begin{array}[t]{rll}
\dfrac{A_{\text{Torräume}}}{A_{\text{Gesamt}}}&=& \dfrac{149,10\,\text{m}^2}{800,00\,\text{m}^2}\\[5pt]
&\approx&0,186\\[5pt]
&=& 18,6\,\%
\end{array}\)](https://mathjax.schullv.de/8ffa9343b74cbbd71ec6647718331d30476aa54d9d3e07a52f0ee4800f1b1d58?color=5a5a5a) Die Flächen der beiden Torräume bilden gemeinsam ca.
Die Flächen der beiden Torräume bilden gemeinsam ca.  der gesamten Spielfeldfläche.
der gesamten Spielfeldfläche.
Beide Torräume setzen sich gemeinsam zusammen aus
- vier Viertelkreisen mit dem Radius
die gemeinsam den Flächeninhalt eines Kreises mit dem Radius
haben,
- und zwei Rechtecken mit den Seitenlängen
und

Skizze
3.2.1
Höhe des Abwurfs berechnen
Der Torwart wirft den Ball im Punkt  ab. Der
ab. Der  -Wert der Funktion
-Wert der Funktion  gibt die Höhe des Balls über dem Spielfeld an.
Der Torwart wirft den Ball in einer Höhe von
gibt die Höhe des Balls über dem Spielfeld an.
Der Torwart wirft den Ball in einer Höhe von  ab.
Größte Höhe des Balls bestimmen
Bei dem Graphen der Funktion
ab.
Größte Höhe des Balls bestimmen
Bei dem Graphen der Funktion  handelt es sich um eine nach unten geöffnete Parabel. Der Punkt, an dem sich der Ball am höchsten befindet, wird daher durch den Scheitelpunkt der Parabel beschrieben.
handelt es sich um eine nach unten geöffnete Parabel. Der Punkt, an dem sich der Ball am höchsten befindet, wird daher durch den Scheitelpunkt der Parabel beschrieben.
 Casio Classpad II
Casio Classpad II
 Die größte Höhe des Balls über dem Spielfeld beträgt also
Die größte Höhe des Balls über dem Spielfeld beträgt also 
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
Der CAS liefert die Koordinaten des Scheitelpunkts
3.2.2
Der Auftreffpunkt des Balls auf dem Boden wird durch den Punkt beschrieben, in dem der Graph von  für
für  die
die  -Achse schneidet. Gesucht ist also die passende Nullstelle der Funktion
-Achse schneidet. Gesucht ist also die passende Nullstelle der Funktion  Der solve-efehl des CAS liefert für
Der solve-efehl des CAS liefert für  die Lösungen
die Lösungen  und
und  Aufgrund des Definitionsbereichs der Funktion ist nur
Aufgrund des Definitionsbereichs der Funktion ist nur  eine zulässige Lösung.
Der Ball würde also nach
eine zulässige Lösung.
Der Ball würde also nach  aufkommen. Addiert man die
aufkommen. Addiert man die  die der Torwart vor der Linie steht, so würde der Ball trotzdem noch im
die der Torwart vor der Linie steht, so würde der Ball trotzdem noch im  langen Spielfeld aufkommen.
langen Spielfeld aufkommen.
3.2.3
Der Mittelpunkt der linken Torlinie wird durch den Punkt  beschrieben, der Mittelpunkt der rechten Torlinie durch
beschrieben, der Mittelpunkt der rechten Torlinie durch  Die beiden Freiwurflinien sind in jedem Punkt genau
Die beiden Freiwurflinien sind in jedem Punkt genau  Meter von der jeweiligen Torlinie entfernt. Auf jeder Freiwurflinie gibt es genau einen Punkt, der senkrecht unterhalb der Flugbahn des Balls liegt. Diese beiden Punkte haben im Koordinatensystem die Koordinaten
Meter von der jeweiligen Torlinie entfernt. Auf jeder Freiwurflinie gibt es genau einen Punkt, der senkrecht unterhalb der Flugbahn des Balls liegt. Diese beiden Punkte haben im Koordinatensystem die Koordinaten  und
und  Der Ball wird in einer Höhe von
Der Ball wird in einer Höhe von  gefangen. Gesucht ist also der
gefangen. Gesucht ist also der  -Wert zum
-Wert zum  Mit dem solve-Befehl des CAS folgt
Mit dem solve-Befehl des CAS folgt  Die zweite Lösung
Die zweite Lösung  liegt außerhalb des Spielfeldes.
Der Ball wird also in dem Punkt gefangen, der im Koordinatensystem durch
liegt außerhalb des Spielfeldes.
Der Ball wird also in dem Punkt gefangen, der im Koordinatensystem durch  beschrieben wird. Dieser Punkt liegt senkrecht über dem Punkt
beschrieben wird. Dieser Punkt liegt senkrecht über dem Punkt  der den Punkt auf der rechten Freiwurflinie senkrecht unterhalb der Flugbahn des Balls beschreibt.
Der Ball wird also senkrecht über der Freiwurflinie gefangen.
der den Punkt auf der rechten Freiwurflinie senkrecht unterhalb der Flugbahn des Balls beschreibt.
Der Ball wird also senkrecht über der Freiwurflinie gefangen.
3.3
Die Wahrscheinlichkeit, dafür dass Marian einen Siebenmeterwurf hält, beträgt  dafür dass er einen Siebenmeterwurf nicht hält also
dafür dass er einen Siebenmeterwurf nicht hält also  Mit den Pfadregeln ergibt sich:
Mit den Pfadregeln ergibt sich:
![\(\begin{array}[t]{rll}
P(A)&=& 3\cdot 0,22\cdot 0,78\cdot 0,78 \\[5pt]
&\approx& 0,402\\[5pt]
&=& 40,2\,\%\\[10pt]
P(B)&=& 0,78\cdot 0,78\cdot 0,78 \\[5pt]
&\approx& 0,475\\[5pt]
&=& 47,5\,\%
\end{array}\)](https://mathjax.schullv.de/020e5d06e35a248f3e8ecd4f043edd5bd9f7c00c855cb4a71066f6faf7b07775?color=5a5a5a) Mit einer Wahrscheinlichkeit von ca.
Mit einer Wahrscheinlichkeit von ca.  hält Marian genau einen von drei Siebenmeterwürfen. Mit einer Wahrscheinlichkeit von ca.
hält Marian genau einen von drei Siebenmeterwürfen. Mit einer Wahrscheinlichkeit von ca.  hält er keinen von drei Siebenmeterwürfen.
hält er keinen von drei Siebenmeterwürfen.