Teil B
1
Die Abbildung zeigt den Graphen der in  definierten Funktion
definierten Funktion 
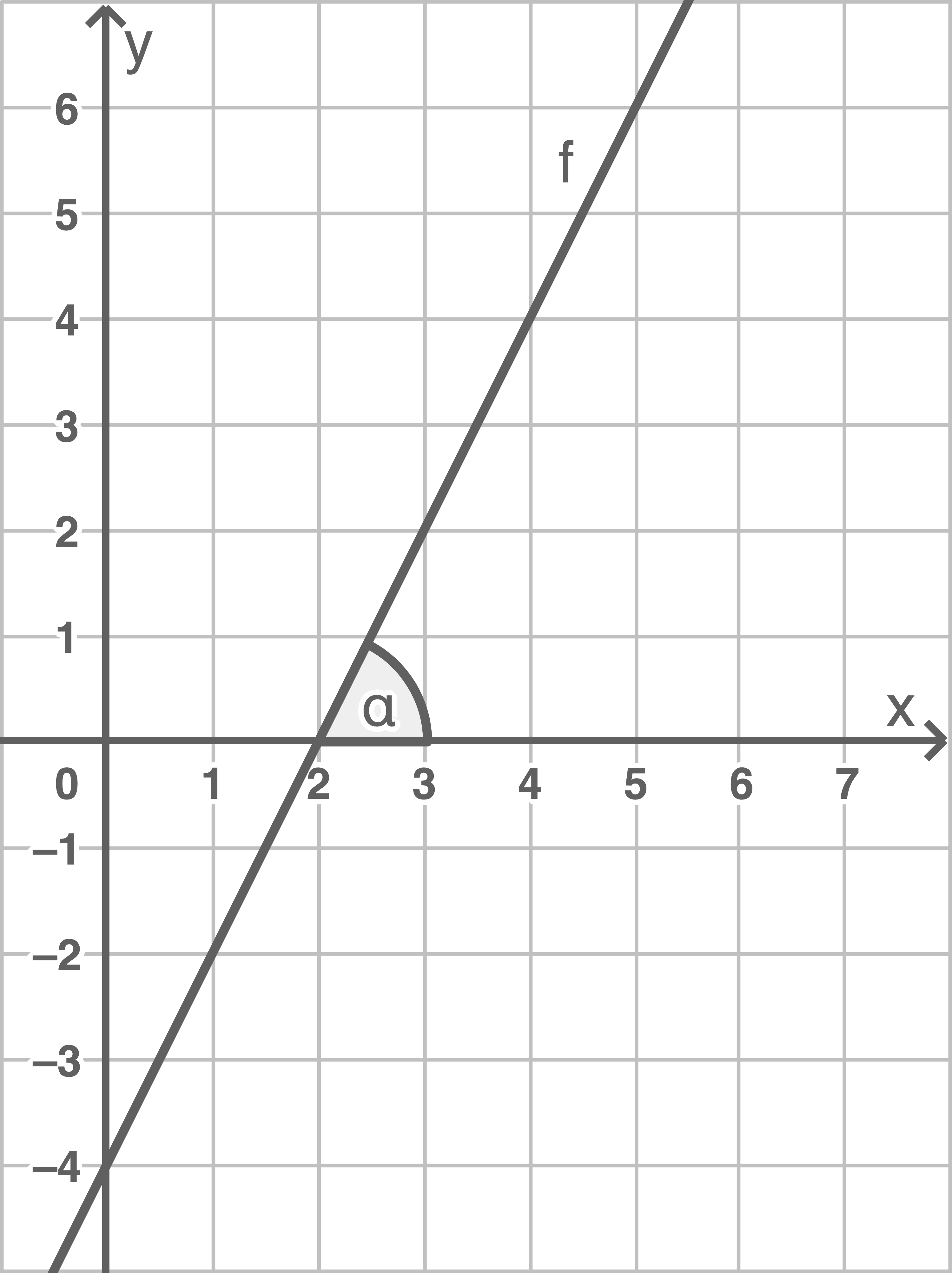

1.1
Gib den Funktionswert für  sowie das Argument für den Funktionswert
sowie das Argument für den Funktionswert  an.
an.
(2 BE)
1.2
Berechne die Größe des Winkels 
(2 BE)
1.3
Der Graph der linearen Funktion  schneidet den Graphen von
schneidet den Graphen von  senkrecht im Punkt
senkrecht im Punkt  Zeichne den Graphen von
Zeichne den Graphen von  in die Abbildung ein.
in die Abbildung ein.
Gib eine Funktionsgleichung für an.
an.
Gib eine Funktionsgleichung für
(3 BE)
1.4
Ermittle die Koordinaten des Schnittpunkts der Graphen der in  definierten Funktionen
definierten Funktionen  und
und  mit
mit  sowie
sowie 
(2 BE)
2
Antons Klasse macht eine Klassenfahrt.
2.1
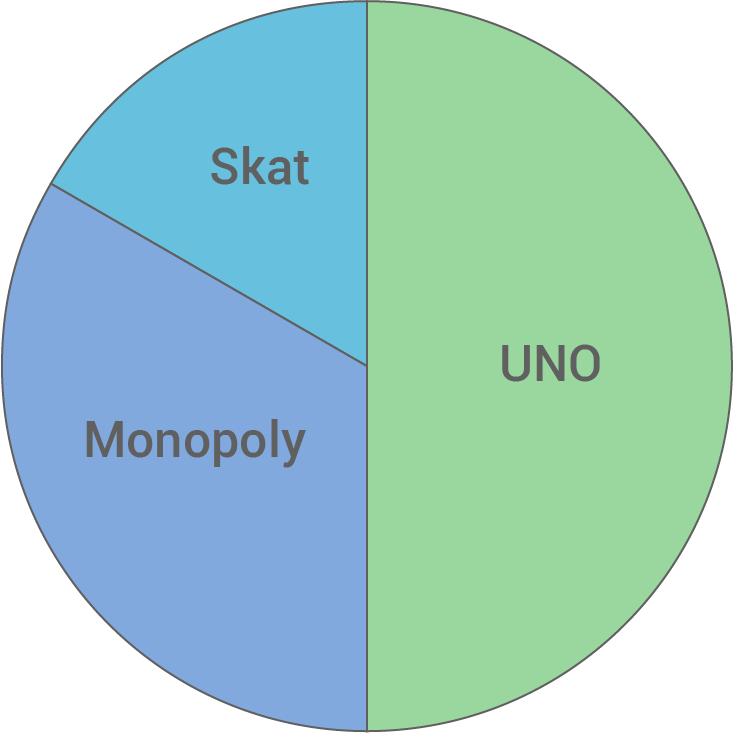
Zur Vorbereitung eines Spielenachmittags haben alle 24 Schüler der Klasse ihr Lieblingsspiel angegeben. Dabei nannten 12 Schüler das Spiel UNO, 8 Monopoly und 4 Skat.
Stelle die Anteile der genannten Lieblingsspiele in einem Kreisdiagramm dar.
(2 BE)
2.2
Am Spielenachmittag spielt Anton mit Freunden UNO. Ein UNO-Spiel hat insgesamt 108 Karten; davon sind 8 Farbwahlkarten. Die Karten werden einzeln nacheinander zufällig ausgeteilt.
Gib die Wahrscheinlichkeit dafür an, dass die erste ausgeteilte Karte eine Farbwahlkarte ist.
Bestimme die Wahrscheinlichkeit des Ereignisses „Die erste ausgeteilte Karte ist keine Farbwahlkarte und die zweite ausgeteilte Karte ist eine Farbwahlkarte“.
(3 BE)
2.3
Anton hat an den vier Tagen der Klassenfahrt von seinem Taschengeld folgende Beträge ausgegeben:
 im Sachzusammenhang an.
im Sachzusammenhang an.
- 1.Tag:
- 2.Tag:
- 3.Tag:
- 4.Tag:
(1 BE)
3
Das Hotel The Westin, das City-Hochhaus und das Wintergartenhochhaus gehören zur Skyline von Leipzig.
3.1
Die Abbildung zeigt vereinfacht die Seitenfläche  des City-Hochhauses.
des City-Hochhauses.
 Ein Koordinatensystem wird so in diese Seitenfläche gelegt, dass der Koordinatenursprung im Punkt
Ein Koordinatensystem wird so in diese Seitenfläche gelegt, dass der Koordinatenursprung im Punkt  liegt. Eine Längeneinheit im Koordinatensystem entspricht
liegt. Eine Längeneinheit im Koordinatensystem entspricht  in der Realität. Die Profillinie von
in der Realität. Die Profillinie von  nach
nach  wird näherungsweise durch den Graphen der Funktion
wird näherungsweise durch den Graphen der Funktion  mit
mit 
 beschrieben.
Die Profillinie des Bodens verläuft entlang der
beschrieben.
Die Profillinie des Bodens verläuft entlang der  -Achse.
-Achse.
Zeige, dass die maximale Höhe der Seitenfläche etwa 
(5 BE)
3.2
Das City-Hochhaus ist für seine Treppenläufe bekannt. Dabei müssen die Läufer 700 Stufen überwinden. Falk und Nina nehmen am Treppenlauf teil.
3.2.1
Die Tabelle gibt für Falk die Anzahl der überwundenen Stufen zu unterschiedlichen Zeiten an.
Begründe anhand der Tabellenwerte, dass die Anzahl der überwundenen Stufen nicht linear wächst.
| Zeit in Minuten | |||
| Anzahl der überwundenen Stufen |
(1 BE)
3.2.2
Die Funktion  mit
mit  beschreibt für Nina näherungsweise die Anzahl der nach dem Start überwundenen Stufen zur Zeit
beschreibt für Nina näherungsweise die Anzahl der nach dem Start überwundenen Stufen zur Zeit  (
(  in Minuten).
Ermittle, nach welcher Zeit Nina alle 700 Stufen bewältigt hat.
Bestimme die Anzahl der von Nina überwundenen Stufen 6 Sekunden nach dem Start.
in Minuten).
Ermittle, nach welcher Zeit Nina alle 700 Stufen bewältigt hat.
Bestimme die Anzahl der von Nina überwundenen Stufen 6 Sekunden nach dem Start.
(4 BE)
3.3
Die Abbildung zeigt die Fußpunkte vom Hotel The Westin  vom City-Hochhaus
vom City-Hochhaus  und vom Wintergartenhochhaus
und vom Wintergartenhochhaus  auf dem ebenen Boden.
auf dem ebenen Boden.
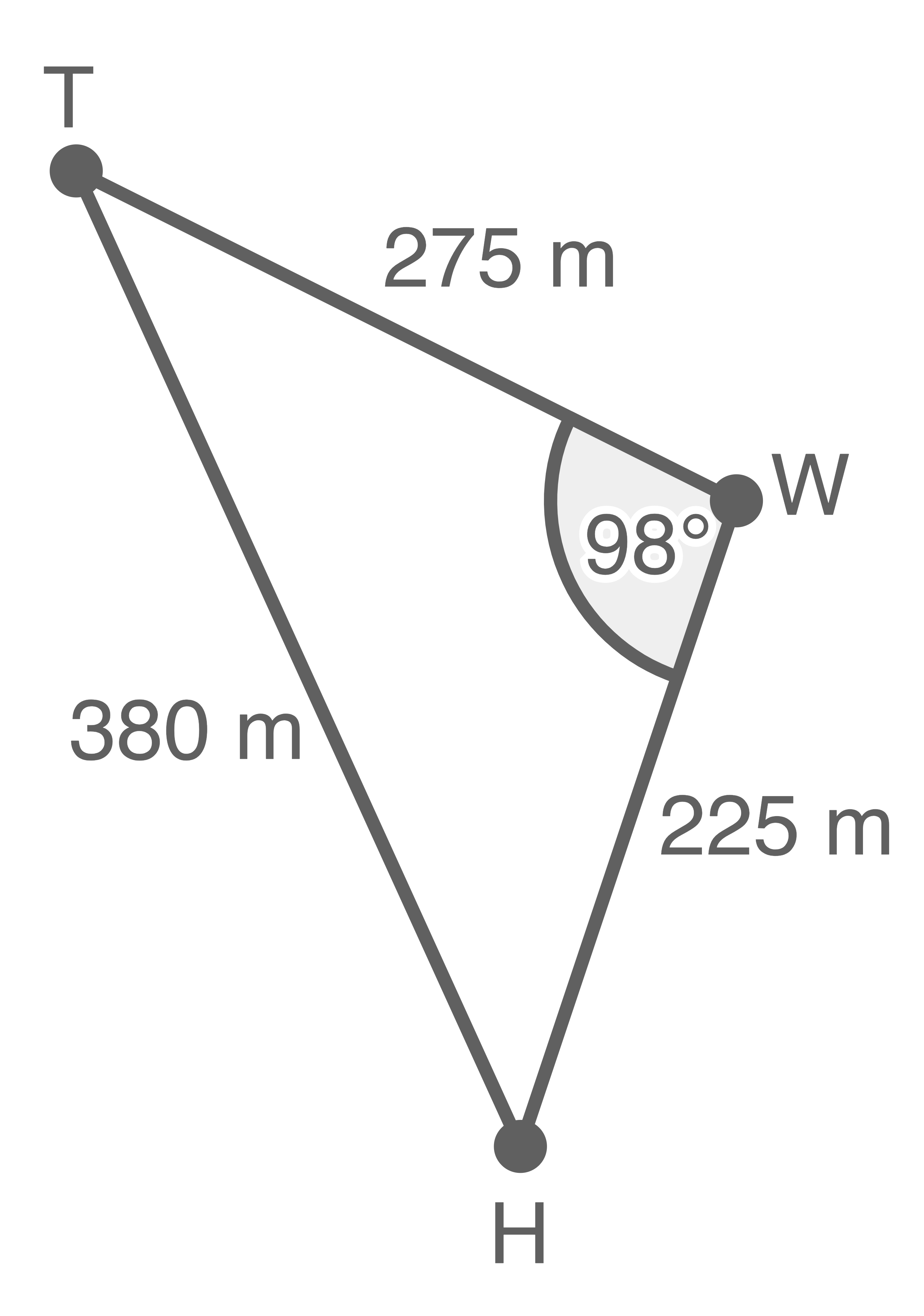

3.3.1
Berechne die Größe des Winkels 
(2 BE)
3.3.2
Senkrecht über dem Fußpunkt des Wintergartenhochhauses (W) befindet sich auf dem Dach in  Höhe über dem Boden der Punkt
Höhe über dem Boden der Punkt  Von
Von  aus sieht man in einer Entfernung von
aus sieht man in einer Entfernung von  die höher gelegene Spitze
die höher gelegene Spitze  der Antenne des City-Hochhauses, welche sich senkrecht über dem Fußpunkt des City-Hochhauses
der Antenne des City-Hochhauses, welche sich senkrecht über dem Fußpunkt des City-Hochhauses  befindet.
Berechne die Höhe der Spitze
befindet.
Berechne die Höhe der Spitze  über dem Boden.
über dem Boden.
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
1.2
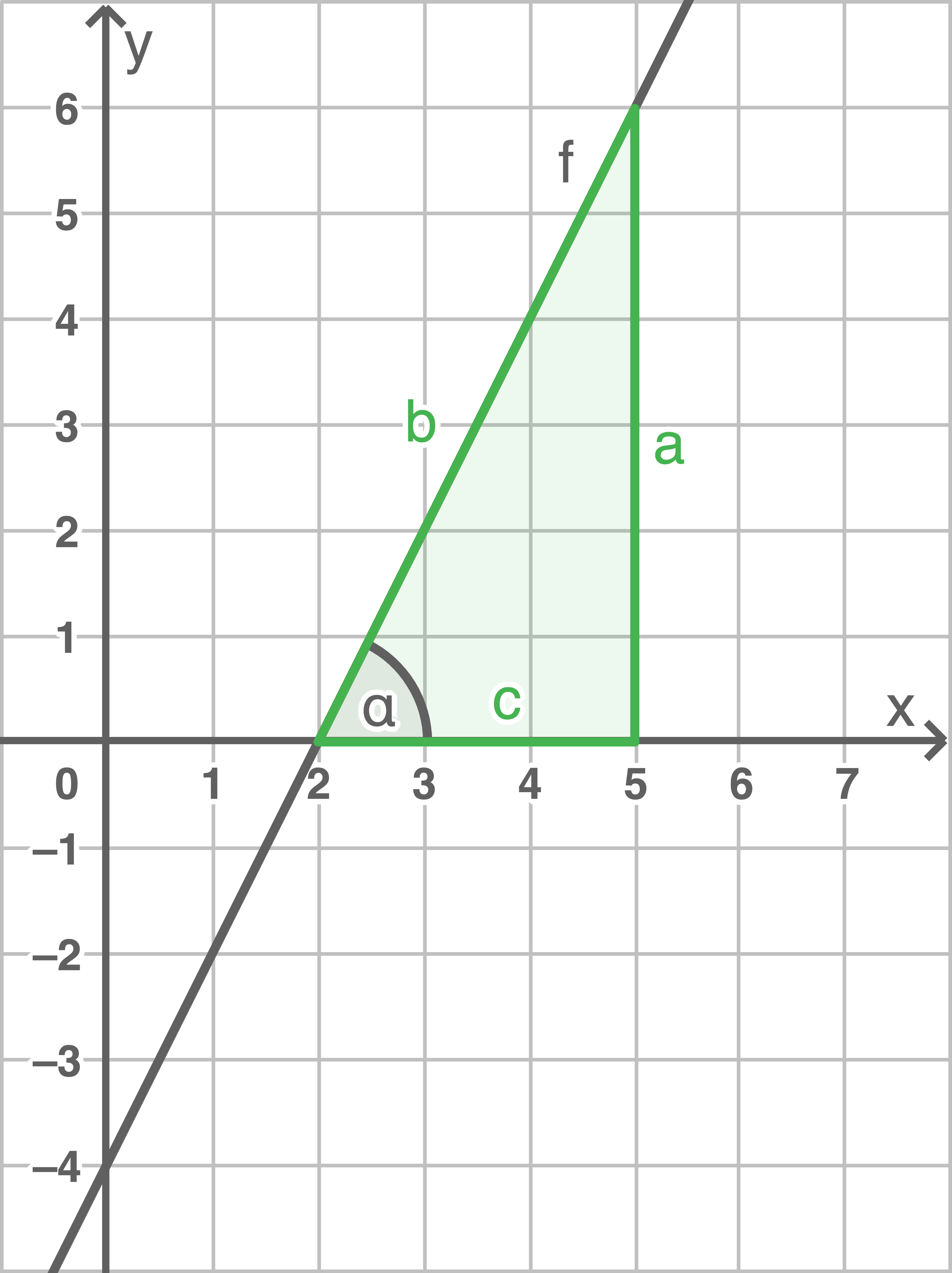
Hilfsskizze
1.3
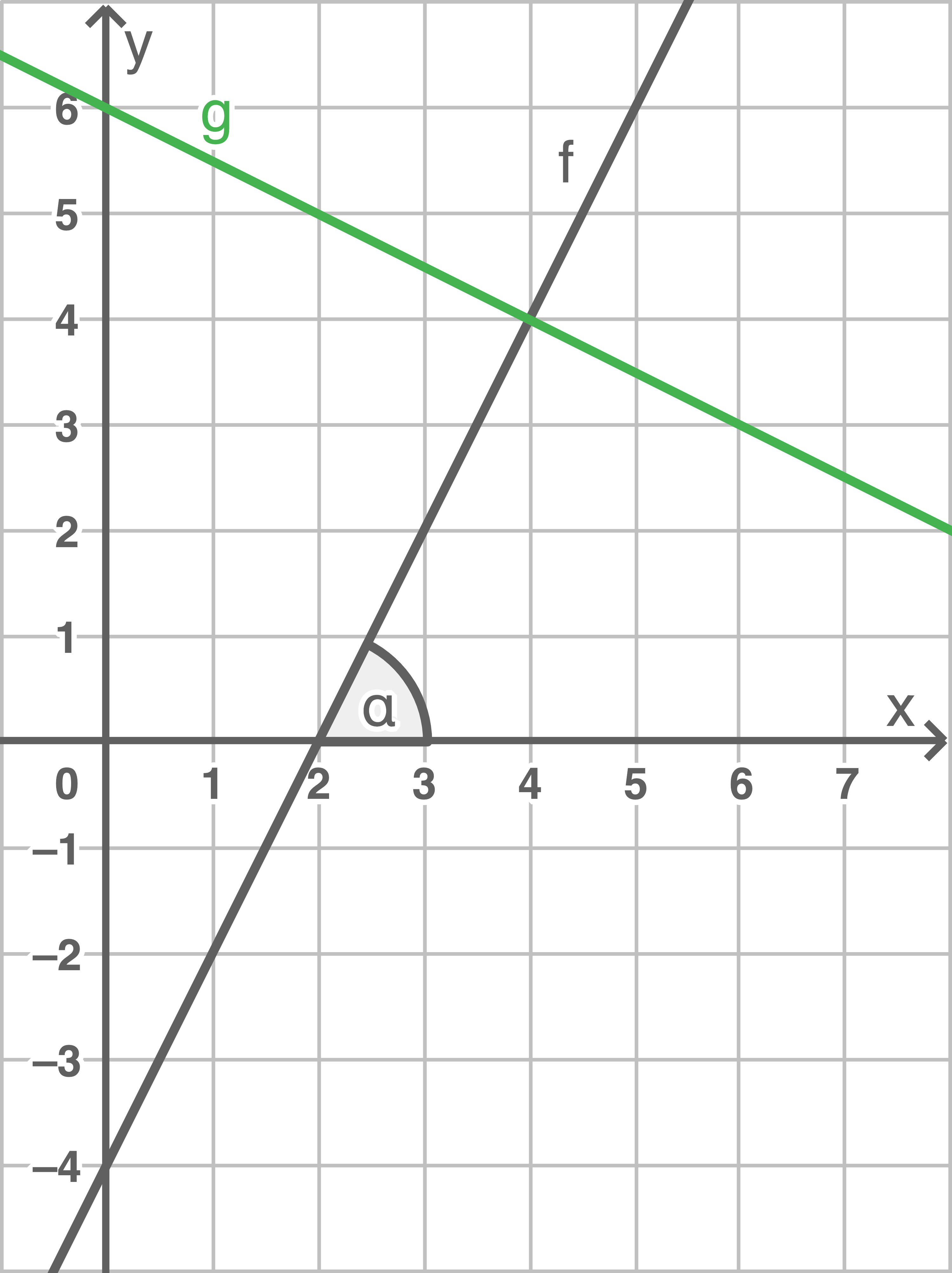
Graph von 
1.4
Gleichsetzen der beiden Funktionsterme:
![\(\begin{array}[t]{rll}
h(x) &=& k(x) \\[5pt]
3\cdot x+225 &=& \dfrac{3}{4}\cdot x+162 \quad \scriptsize \mid\; -225 \\[5pt]
3\cdot x &=& \dfrac{3}{4}\cdot x -63 \quad \scriptsize \mid\; -\dfrac{3}{4}\cdot x \\[5pt]
\dfrac{9}{4}\cdot x &=& -63 \quad \scriptsize \mid\; \cdot \dfrac{4}{9}\\[5pt]
x &=& -28
\end{array}\)](https://mathjax.schullv.de/27ebda1875c6512f26ba6953c94ae5a3589c2737fd03222c41e057609410bbe7?color=5a5a5a) Mit
Mit  ergeben sich die Koordinten des Schnittpunkts:
ergeben sich die Koordinten des Schnittpunkts: 
2.1
2.2
Wahrscheinlichkeit angeben, dass die erste ausgeteilte Karte eine Farbwahlkarte ist
 Wahrscheinlichkeit des Ereignisses bestimmen
Wahrscheinlichkeit des Ereignisses bestimmen

2.3
Der Term gibt den Wert an, den Anton an einem Tag im Durchschnitt ausgegeben hat.
3.1
Zeigen, dass maximale Höhe  m beträgt
Der höchste Punkt der Seitenfläche wird durch den Punkt
m beträgt
Der höchste Punkt der Seitenfläche wird durch den Punkt  beschrieben. Die
beschrieben. Die  -Koordinate von
-Koordinate von  ist
ist  Für den zugehörigen Funktionswert gilt:
Für den zugehörigen Funktionswert gilt:
 Da eine Längeneinheit im Koordinatensystem
Da eine Längeneinheit im Koordinatensystem  in der Realität entspricht, beträgt die maximale Höhe der Seitenfläche
in der Realität entspricht, beträgt die maximale Höhe der Seitenfläche  Höhe des Punktes
Höhe des Punktes  über dem Boden angeben
über dem Boden angeben
 Der Punkt
Der Punkt  befindet sich somit
befindet sich somit  über dem Boden.
Näherungswert für den Flächeninhalt ermitteln
über dem Boden.
Näherungswert für den Flächeninhalt ermitteln
Die Seitenfläche kann wie in der Skizze unten unterteilt werden.
 Der Flächeninhalt des Rechtecks
Der Flächeninhalt des Rechtecks  lässt sich wie folgt berechnen:
lässt sich wie folgt berechnen:
 Die Fläche
Die Fläche  kann näherungsweise als Dreieck betrachtet werden. Für den Flächeninhalt gilt dann:
kann näherungsweise als Dreieck betrachtet werden. Für den Flächeninhalt gilt dann:
![\(\begin{array}[t]{rll}
A_{CDE}&\approx& \dfrac{1}{2}\cdot 33\,\text{m}\cdot (142,5\,\text{m}-120\,\text{m}) \\[5pt]
&=& 371,25\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/cfd09f9cb4e3f5c909c2516482444115da467a3a2fbd8986496f02d18369bf56?color=5a5a5a) Der Flächeninhalt der gesamten Seitenfläche kann näherungsweise wie folgt berechnet werden:
Der Flächeninhalt der gesamten Seitenfläche kann näherungsweise wie folgt berechnet werden:
![\(\begin{array}[t]{rll}
A&=& A_{ABDE}+A_{CDE} \\[5pt]
&\approx& 3960\,\text{m}^2+371,25\,\text{m}^2 \\[5pt]
&=& 4331,25\,\text{m}^2
\end{array}\)](https://mathjax.schullv.de/4b874f08d746c51a8284ee01518fc67fd7ce50e6938060d06016d232d0739a66?color=5a5a5a)

Hilfsskizze
3.2.1
Würde die Anzahl der überwundenen Stufen linear wachsen, müsste in jeder Minute die gleiche Anzahl an Stufen überwunden werden. Nach zwei Minuten entspräche dies  Stufen und damit mehr als tatsächlich überwunden wurden.
Stufen und damit mehr als tatsächlich überwunden wurden.
3.2.2
Ermitteln, nach welcher Zeit Nina  Stufen bewältigt hat
Gesucht ist die Lösung der Gleichung
Stufen bewältigt hat
Gesucht ist die Lösung der Gleichung 
![\(\begin{array}[t]{rll}
-750\cdot \mathbb e^{-0,3\cdot t}+750&=& 700 \quad \scriptsize \mid\; -750 \\[5pt]
-750\cdot \mathbb e^{-0,3\cdot t}&=& -50 \quad \scriptsize \mid\; :(-750) \\[5pt]
\mathbb e^{-0,3\cdot t}&=& \dfrac{1}{15} \quad \scriptsize \mid\; \ln \\[5pt]
-0,3\cdot t&\approx& -2,7 \quad \scriptsize \mid\; :(-0,3) \\[5pt]
t&\approx& 9
\end{array}\)](https://mathjax.schullv.de/faf785d813de9e8dcd64af204725902f2cdcb982d26d961b7941d5b71352ef10?color=5a5a5a) Nach
Nach  Minuten hat Nina alle
Minuten hat Nina alle  Stufen bewältigt.
Anzahl überwundender Stufen nach
Stufen bewältigt.
Anzahl überwundender Stufen nach  Sekunden ermitteln
Sekunden ermitteln
 Sekunden entsprechen
Sekunden entsprechen  Minuten.
Minuten.

 Sekunden nach dem Start hat Nina
Sekunden nach dem Start hat Nina  Stufen überwunden.
Stufen überwunden.
3.3.1
Mit dem Sinussatz gilt:
![\(\begin{array}[t]{rll}
\dfrac{380}{\sin(98^{\circ})}&=& \dfrac{275}{\sin(\sphericalangle WHT)} \quad \scriptsize \mid\; ()^{-1} \\[5pt]
\dfrac{\sin(98^{\circ})}{380}&=& \dfrac{\sin(\sphericalangle WHT)}{275} \quad \scriptsize \mid\; \cdot 275 \\[5pt]
\dfrac{\sin(98^{\circ})}{380}\cdot 275&=& \sin(\sphericalangle WHT)\\[5pt]
0,72&\approx& \sin(\sphericalangle WHT) \quad \scriptsize \mid\; \sin^{-1} \\[5pt]
46^{\circ}&\approx& \sphericalangle WHT
\end{array}\)](https://mathjax.schullv.de/fd1ec9d0d595c57374183f0b9c40499cf22ca6fb88bb297aae3372c7bf7ee037?color=5a5a5a) Der Winkel
Der Winkel  beträgt ungefähr
beträgt ungefähr 
3.3.2
Gesucht ist die Länge der Strecke  in der Abbildung unten.
in der Abbildung unten.
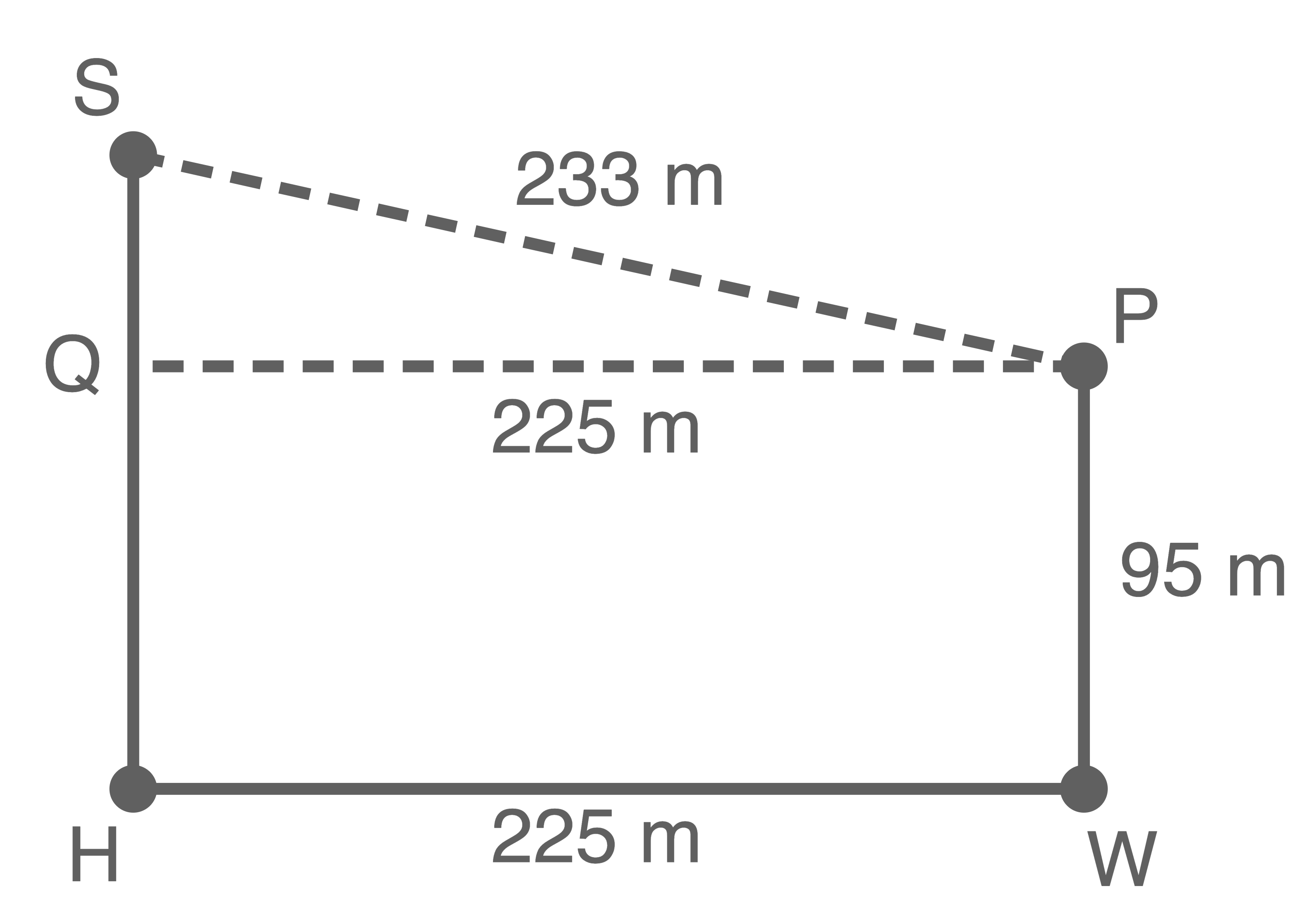 Die Länge der Strecke
Die Länge der Strecke  beträgt dabei
beträgt dabei  Die Länge der Strecke
Die Länge der Strecke  lässt sich mit dem Satz des Pythagoras berechnen:
lässt sich mit dem Satz des Pythagoras berechnen:
![\(\begin{array}[t]{rll}
225^2+\overline{QS}^2&=& 233^2 \quad \scriptsize \mid\; -225^2 \\[5pt]
\overline{QS}^2&=& 233^2-225^2 \\[5pt]
\overline{QS}^2&=& 3664 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
\overline{QS}&\approx& 60,5 [\text{m}]
\end{array}\)](https://mathjax.schullv.de/62cd5dcc07b5a53bcda4243c35b91ce9618d03b44930ba23401b78d07698f1a2?color=5a5a5a) Damit gilt für die Länge der Strecke
Damit gilt für die Länge der Strecke 
![\(\begin{array}[t]{rll}
\overline{HS}&=& \overline{HQ}+\overline{QS} \\[5pt]
&=& 95\,\text{m}+ 60,5\,\text{m} \\[5pt]
&=& 155,5\,\text{m}
\end{array}\)](https://mathjax.schullv.de/beb0cb91cd2345e84c17ac6012b03c1c9761b4979b6b18e3c6eabedcf3172138?color=5a5a5a)

Hilfsskizze